风积沙路基填料累积塑性应变及预测模型
2022-10-22聂如松钱冲刘婞阮波祁延录赵加海
聂如松,钱冲,刘婞,阮波,祁延录,赵加海
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中南大学 重载铁路工程结构教育部重点实验室,湖南 长沙 410075;3. 新疆铁道勘察设计院有限公司,新疆 乌鲁木齐 830011)
风积沙具有颗粒均匀、结构松散、保水性差、天然含水率小以及抗剪强度低[1]等特点。将风积沙用于铁路建设中,需对风积沙的力学特性进行研究,获得风积沙相关的力学参数,为铁路设计和施工提供理论依据。国内外学者对风积沙开展了大量研究工作,取得了一定结果,但研究主要集中在风积沙的压实特性、静力性能以及风积沙的改良等方面。袁玉卿等[2]对风积沙的压实特性开展研究,发现风积沙击实曲线在含水率为0和最优含水率下达到峰值,呈横倒的“S”型。风积沙的最佳振动频率为45~50 Hz。采用干压实工艺,现场压实系数能达到0.96。阮波等[3-5]对不同养护温度条件下水泥改良风积沙无侧限抗压强度开展试验研究,发现水泥掺量5%的风积沙改良土能满足铁路基床底层填料的设计要求。ANISUR[6]采用普通硅酸盐水泥(OPC)作为稳定剂,硅灰(SF)作为添加剂对风积沙进行改良,研究其最大干密度、最佳含水率、无侧限抗压强度等,并建议硅灰/水泥(SF/C)最优比率是0.20。动荷载作用引起不断累积的塑性变形是铁路运行条件恶化的主要原因[7]。国内外研究者对路基土累积塑性变形的预测模型开展了大量的研究,具有代表性的成果有LENTZ[8]提出的半对数经验模型、MONISMITH 等[9]提出的指数经验模型和黄茂松等[10]提出的相对偏应力水平经验模型等。因模型参数与土体性质、初始应力状态及循环荷载性质等因素有关,其在风积沙的适应性以及各模型参数需要进一步研究确定。综上所述,以往对风积沙的压实特性、静力性能以及风积沙的改良研究较多,但对风积沙填料在列车循环荷载作用下的动力特性研究很少。本文以风积沙填料为对象,开展风积沙在列车动荷载作用下的动三轴试验,系统研究风积沙累积塑性应变随动应力幅值、围压和含水率的变化规律,发展考虑动应力幅值、含水率及围压的风积沙累积塑性应变预测模型,为沙漠铁路设计、施工和运维提供试验依据。
1 动三轴试验
1.1 试验仪器与风积沙填料
试验在DDS-70 动三轴仪上进行。风积沙填料取自新疆和田至若羌铁路。和若铁路是喀和铁路的东延工程,线路长度825 km,设计速度120 km/h,属国铁Ⅰ级铁路,约3/4 的路段穿越流动性沙漠。依据《铁路工程土工试验规程》(TB10102—2010)[11]对土样进行颗粒分析,发现其粒径主要分布在0.075~0.250 mm 之间,含量高达97.2%,大于0.250 mm 的颗粒极少,仅为1.1%,小于0.075 mm的颗粒也只有1.7%。风积沙的级配曲线见图1。不均匀系数Cu=1.93<5,曲率系数Cc=0.91,颗粒级配不良。根据《铁路路基设计规范》(TB10001—2016)[12]可知,风积沙属于C3 组填料。采用固结不排水静三轴剪切试验(CU)得到风积沙抗剪强度指标如表1 所示。其他基本物理性质指标如表2所示。

表1 风积沙的抗剪强度指标Table 1 Shear strength parameters of aeolian sand

表2 风积沙填料基本物理性质指标Table 2 Basic physical property parameters of aeolian sand
铁路路基对压实系数要求较高,基床底层细粒土填料压实度应不小于0.95,和若铁路风积沙多作为基床底层填料使用,结合实际施工情况试验选择压实度K=0.95。试样直径为39.1 mm,高度80 mm。试样采取击实方法制样。为保证制样均匀,分5层击实完成,通过控制每层土质量保证压实系数,每层进行刮毛处理以避免土样分层。制样过程依据《铁路工程土工试验规程》(TB10102—2010)[11]和《土工试验方法标准》(T50123—2019)[13]执行。值得注意的是,因风积沙强度低、黏聚力小,制样时不要在饱和器底部垫滤纸及四周涂抹凡士林,制样完成立即开展实验,以避免取样时大量沙土粘在饱和器四周,造成试样不完整、麻面。
1.2 试验方案
为模拟路基不同深度处的侧压环境,本次循环荷载动三轴试验围压为σ3=15,30 和60 kPa,大致代表路基面、路基面以下1.5 m 和2.5 m 处的填料(基床厚度为2.5 m)。含水率考虑3种状态,即最优含水率、饱和含水率和天然含水率。和若铁路为客货共线铁路,设计时速120 km,我国客车标准车厢车体长度为23.6 m,按公式f=v/l换算成列车荷载对路基的主要加载频率f=1.4 Hz;货车运行速度一般为50~80 km/h,货车车厢C70 和C80 的车体长度为13.976 m,换算成列车荷载对路基的主要加载频率f=0.99~1.59 Hz[14-15]。考虑到和若铁路将来客车的实际运速和试验加载的方便,试验加载频率取f=1.0 Hz。30 t 轴重的重载列车运行条件下对路基面产生的最大动应力在90 kPa左右[16],考虑风积沙在铁路路基中可能填筑的部位(不考虑基床表层填料)和列车荷载的大小,试验加载中动应力幅值σd=30,60 和90 kPa。根据前期试验结果发现振次N达到2 000 次可满足对风积沙动力特性研究目的,另考虑仪器性能和相关研究[17],本试验加载最大振次为2 000次。
试样进行等压固结。对饱和试样,当超孔隙水压力小于1 kPa 时即认为固结完成。对非饱和试样,当固结约2 h 后,试样轴向位移达到稳定状态时即认为固结完成。试验采用应力控制加载方式,考虑到加荷时间较短和偏于安全的角度考虑,加载过程中不允许试样排水。轨道结构自重作用在路基面上的静荷载σs=15 kPa,由于风积沙不考虑作为基床表层填料,作用在路基面上的静荷载需要经过0.6 m 厚基床表层的应力扩散,传递到基床底层表面的静压力约12.75 kPa。考虑到静荷载相差不大,在加载过程中仍然以σs=15 kPa实施加载。施加完静偏应力后再施加正弦动荷载,其中,σd为动应力幅值。试验加载如图2 所示。图中,AB段表示围压施加阶段,BC表示固结阶段,CD段为铁路上部轨道结构和基床表层施加的静荷载,即σs,DE为循环荷载阶段。
试验终止条件为:当循环振次达到2 000 次或应变达到5%[13]即停止试验,稳定标准为1 h内试样累积塑性应变增量少于0.2%,即累积塑性应变变化速率少于0.2%/h[18-19],具体的动三轴试验方案见表3。

表3 动三轴试验方案Table 3 Test program of dynamic triaxial test
2 试验结果与分析
2.1 循环荷载下试样轴向应变随振次变化规律
以最优含水率wopt=14.0%试样为例,说明循环荷载作用下风积沙试样的轴向应变随循环振次的变化规律,如图3所示。
由图3 可知,风积沙试样在循环荷载作用下,轴向应变呈周期上升。在每个周期(1 s)内,试样的轴向应变先增大后减小;任意时刻,轴向应变由可恢复的弹性应变εe和永久的塑性应变εp组成,塑性应变εp随循环振次的增加不断积累。
加载初期,动荷载作用下风积沙颗粒内部发生较大错动,轴向应变增长较快,随着振次增加,图3(b)应变增长逐渐减缓,曲线渐趋平稳,达到2 000振次时,轴向应变为3.89%。图3(a)轴向应变一直发展迅速,曲线有明显的周期波动,累积塑性应变积累较快,在50振次内轴向应变就达到5%停止试验。
2.2 累积塑性应变随振次的变化规律
以最优含水率wopt=14.0%的风积沙试样为例,在循环荷载作用下的累积塑性应变εp与循环次数N之间的关系曲线如图4所示。动应力幅值对风积沙的累积塑性应变发展有显著影响,应变随着随动应力幅值的增大而增大,与文献[20]对粗粒土的研究结果一致。根据εp-N曲线的发展规律,εp-N关系曲线分为3 类,分别为稳定型(A 型)、临界型(B型)和破环型(C型)。
A型曲线特征:循环荷载作用下,试样累积塑性应变前期快速增长,经过一定振次后开始趋于稳定,累积塑性应变变化速率少于0.2%/h,累积塑性应变和速率较小,最大应变为1.19%。以图4(b)为例,循环荷载作用下,试样累积塑性应变前期快速增长,在循环振次100次左右开始趋向于稳定,在达到试样终止条件2 000 振次时累积塑性应变较小,动应力幅值30 kPa 和60 kPa 对应的累积塑性应变分别为 0.35%和1.19%。
B 型曲线特征:以图4(b)动应力幅值σd=90 kPa试样为例,循环荷载作用下,试样累积塑性应变初期增长较快,随着振次N的增加,应变增长速率逐渐减缓,在2 000 振次以内试样未破坏,累积塑性应变一直处于增长状态,累积塑性应变变化速率大于0.2%/h,停止试验时累积塑性应变为3.89%,若振次继续增加试样可能趋于稳定也可能破坏。此试样累积塑性变形曲线为B型曲线。
C 型曲线特征:在循环荷载作用下,试样累积塑性应变急剧增长,并在较小振次N情况下应变达到5%发生破坏。图4(a)动应力幅值为60 kPa 试样为C型曲线。动应力幅值为90 kPa时,试样刚加载就破坏。
2.3 围压对风积沙累积塑性应变的影响
相同动应力幅值下风积沙累积塑性应变和围压的关系曲线,如图5所示。
由图5可知,随着围压的增大,风积沙累积塑性变形逐渐减小。因围压增大,土体颗粒约束和咬合作用增加,微观上表现为加强颗粒间嵌入和啮合,发生相对错动更加困难,宏观上表现为更大的咬合力,故累积塑性应变就越小。
2.4 风积沙塑性变形行为判定准则
WERKMEISTER 等[21-22]基于安定理论,认为可采用5 000 振次和3 000 振次时累积塑性应变之差或累积塑性应变速率发展规律作为塑性变形行为判定准则。利用ε5000p-ε3000p确定塑性变形行为受加载方式、加载振次等影响,不具有普适性。在本研究中,风积沙动三轴试验最大振次为2 000次,显然不能采用5 000 振次和3 000 振次时累积塑性应变之差作为塑性变形行为判定准则,故选用累积塑性应变速率对风积沙的塑性变形行为进行判定。
累积塑性应变速率与振次关系如图6所示,通过对比发现,从第3 振次开始累积塑性应变速率ε̇p与循环振次N的关系曲线可用幂函数很好描述,幂函数表达式为:
ε̇p=αN-β(1)
式中:ε̇p为累积塑性应变速率;N为振动次数;α和β为拟合参数。
结合前文对风积沙动力行为的初步定性分析,通过对比发现,参数β的大小能很好判断风积沙累积塑性应变曲线形态,能定量对风积沙动力行为进一步划分。见表4。参数β越大,试样稳定所需振次越少,视为越稳定,反之试样越容易破坏。β≥0.704 34 时,试样处于稳定状态;β≤0.641 65 时,试样发生破坏;当0.641 65β<0.704 34时,试样为临界状态。图7为风积沙填料累积塑性变形状态分区。为验证该判断准则的适用性,新增压实度K=0.93,围压σ3=30 kPa,含水率wopt=14.0%的补充试验,具体参数见表4。结果如图8~9所示,由图可知,参数β作为累积塑性变形状态判定标准具有较好的准确性。
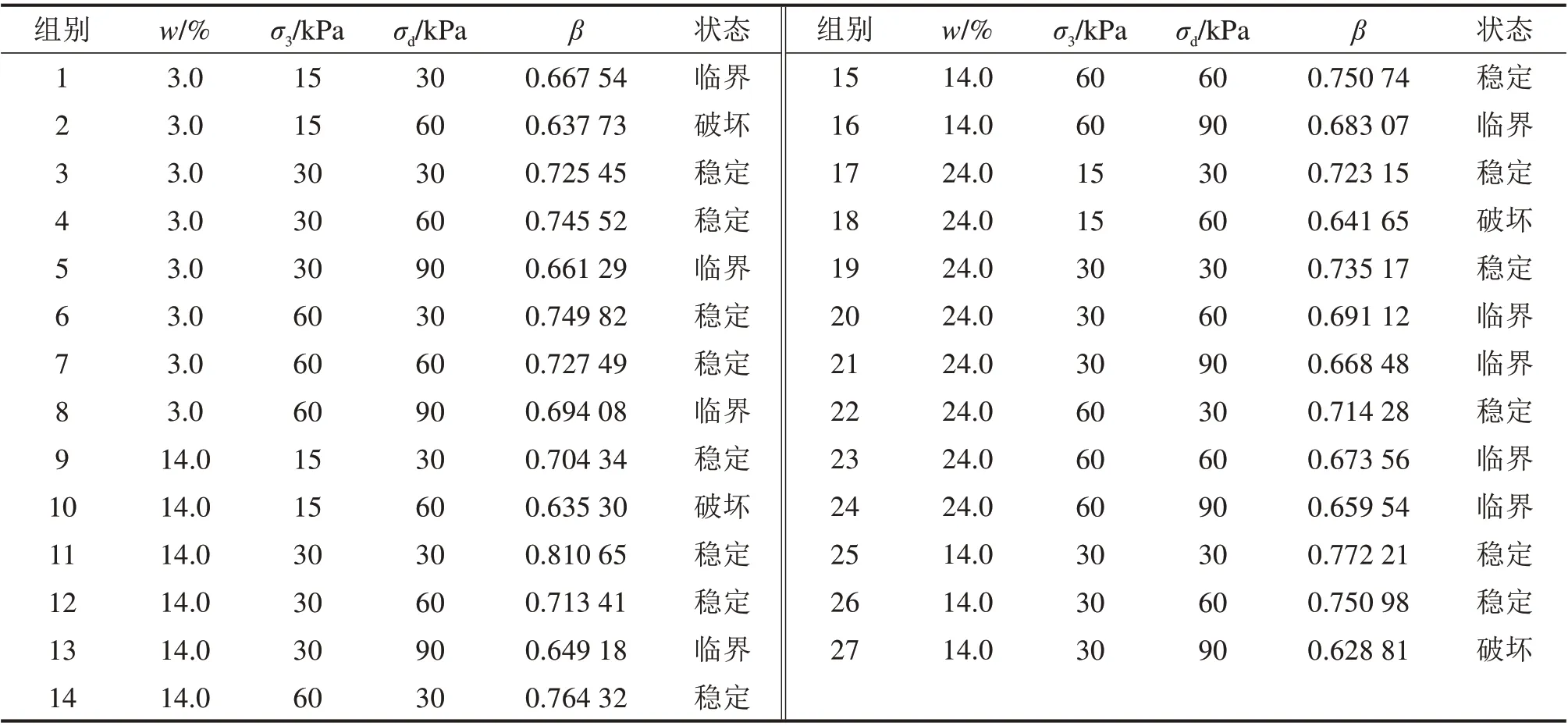
表4 变形状态与拟合参数Table 4 Deformation state and fitting parameters of test samples
2.5 累积塑性应变预测模型
实际铁路工程中路基土体动力行为多处于稳定状态,研究稳定型累积塑性应变对于铁路路基的沉降控制具有重要意义。通过对风积沙累积塑性应变曲线进行拟合分析,如图10 所示(含水率wopt=14%,围压σ3=30 kPa),具体拟合参数见表5,发现半对数模型能较好表示风积沙累积塑性应变,故本文将稳定型和临界型2 种变形行为统一起来,均用半对数模型进行表示,半对数模型基本形式为
εp=a+blgN(2)
式中:a和b为与动应力幅值、围压和土体性质等相关的参数;N为振动次数。
1) 参数a
参数a为第1 次循环荷载加载时产生的累积塑性应变。考虑加载前期不稳定,取第3振次累积塑性应变作为荷载第1次产生的累积塑性应变。图11为最优含水率wopt=14%试验结果a与表5 中a的对比,由图11 可看出试验结果与拟合结果吻合很好。
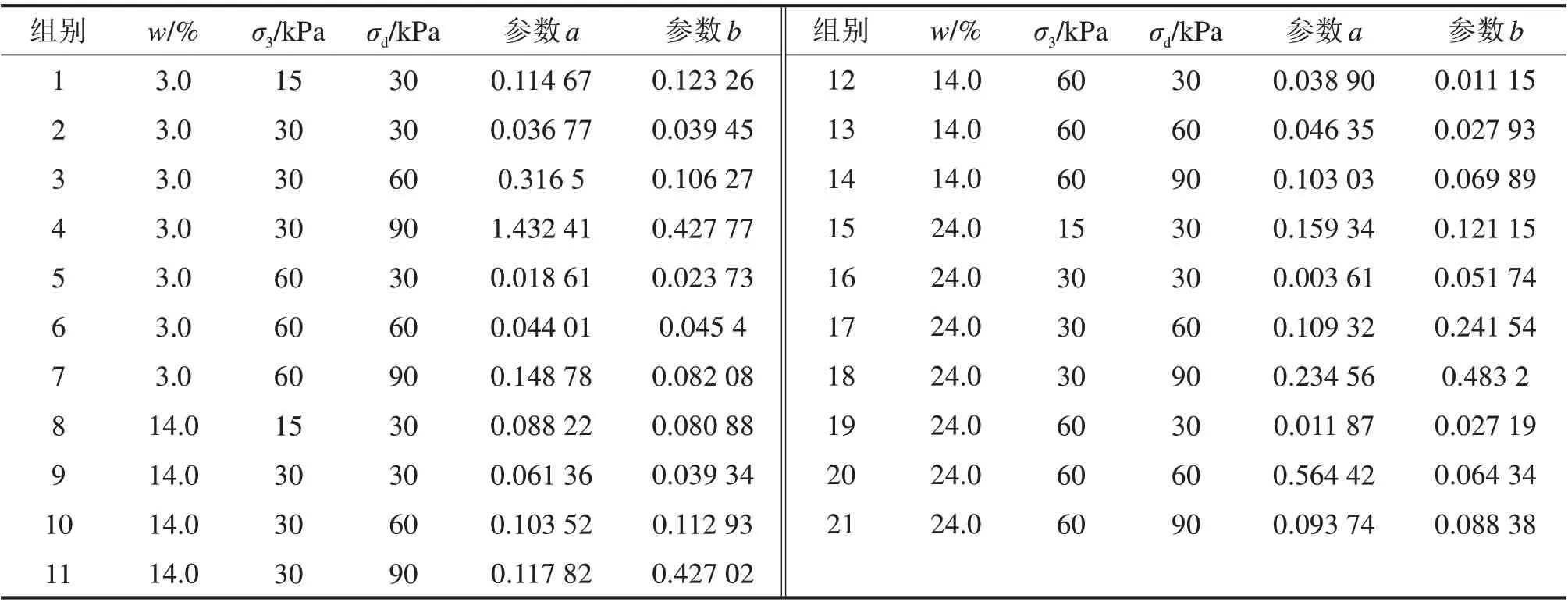
表5 半对数模型拟合参数Table 5 Fitting parameters of half-logarithm model
动静应力比μ是指试样动应力幅值与静强度之比
其中:σf为试样静强度,为静三轴试验试样破坏时的轴向偏应力,即σf=σ1-σ3。已知内摩擦角φ和黏聚力c(如表1),可按式(4)计算,结果如表6所示。
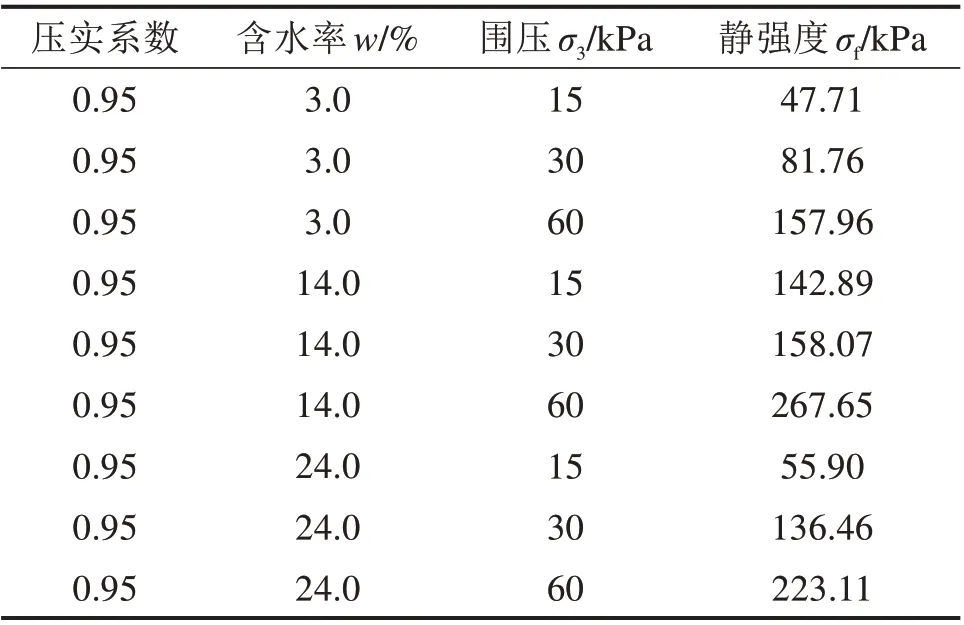
表6 风积沙试样静强度试验值Table 6 Static strength test value of aeolian sand sample
图12 为表5 中参数a与动静应力比μ的关系曲线。从图12 可以看出,动静应力比μ增大,参数a增大。指数函数对其拟合结果很好,拟合度R2=0.959 68,拟合关系为
2) 参数b
参数b反映风积沙试样累积塑性应变与荷载循环振次的关系。动围比η是指试样动应力幅值与围压之比
式中:σd为动应力幅值;σ3为围压。
图13 为表5 中参数b与动围比η的关系曲线。由图13 可看出,随η增大,参数b总体呈上升趋势,指数函数对其拟合结果较好,拟合度R2=0.952 43,拟合关系为
通过式(2)求得含水率wopt=14.0%,N=2 000 振次时试样参数b,将其与拟合值进行对比,如图14所示。由图14 可看出试验结果与拟合结果吻合很好。
将式(3)~(7)代入式(2),得到考虑动应力幅值、含水率以及围压的风积沙稳定型、临界型统一的累积塑性应变预测模型
以不同含水率下围压σ3=30 kPa 及最优含水率下围压σ3=60 kPa 的A和B型曲线为代表,利用式(8)计算出累积塑性应变预测值并与试验值进行对比,如图15所示。
由图15 可见,风积沙累积塑性应变模型能很好地预测风积沙路基累积塑性应变,可为沙漠地区铁路路基设计和施工提供参考。
3 结论
1) 风积沙试样的累积塑性应变εp与循环次数N的关系曲线表现为稳定型、临界型和破环型3 种类型。
2) 幂函数能很好地描述风积沙累积塑性应变速率ε̇p与循环振次N的关系。在此基础上,提出了风积沙填料塑性行为判定准则,即ε̇p=αN_β。
稳定型:β≥0.704 34。
破坏型:β≤0.641 65。
临界型:0.641 65β<0.704 34。
3) 建立了考虑动应力幅值、含水率及围压的风积沙累积塑性应变预测模型,可为风积沙路基在循环动荷载下的沉降预测和基于应变控制原则的路基设计及动力稳定性评估提供参考。
