隧道开挖断面应力变形特性及施工工艺优化研究
2022-10-22滕济伟
滕济伟
(广西桂商实业投资有限公司,广西 南宁 530011)
0 引言
随着我国基建设施的不断拓展与完善,较多的山区隧道项目逐渐开工建设。隧道围岩稳定性关乎隧道安全施工与长期运营,而隧道稳定性与围岩应力变形状态息息相关,由隧道围岩应力变形特性分析确定最优施工方案或工序是当前隧道设计的一种重要技术方法。隧道作为人工开挖结构,在施工过程中需要格外注意围岩应力变形特性,围岩应力变形特性与时间[1]、围岩级别[2]、围岩强度参数[3]等均有一定的联系。隧道围岩稳定性分析中,胡梦涛、刘佳等[4-5]采用理论推导方式,计算获得隧道应力与变形参数变化特征,为分析隧道开挖过程中支护结构、衬砌方式等提供重要依据。当然,相比之下数值仿真计算更能够为高效解决不同施工方案、不同荷载工况等多类型工程提供应力变形分析,采用如ANSYS[6]、FLAC 3D[7]等计算平台,研究隧道断面应力与变形的发展趋势,为工程建设提供重要参考。本文基于隧道围岩应力变形理论计算与仿真分析,探讨施工工艺优化,为工程设计提高施工效率及安全稳定提供计算佐证。
1 工程概况
本工程项目位于广西百色“横5”高速公路乐业段,该隧道全长850 m,采用双洞口进出形式,左右进出洞口半弧圆点之间的距离为15.2 m,与大地水准面高程相比,入口设计绝对高程达1 705.25 m,洞口宽度设计为17.2 m,洞口高达4.8 m,隧道支撑锚杆最深处可达105 m,采用新奥法施工开挖隧道。新奥法施工设备见图1。隧道公路出口设计为拱跨式,出口高度与入口高度相差不大,绝对高程达1 704.68 m,内部公路设计为六车道,按一级高速公路标准设计。隧道开挖采用台阶法施工,超前支护采用砂浆锚杆,选用φ25 mm锚杆材料,锚杆间距为0.8 m,其钢筋网架铺设φ10 mm钢筋,间距为0.7 m;隧道开挖设计为二级防水,围岩铺盖柔性材料,上、下台阶开挖时确保锚杆预应力满足设计要求[8]。初期支护要求锚杆具备40%设计预应力。洞室开挖过程中设置有注浆导管,钻孔厚度为3 mm,以确保支护结构安全稳定。
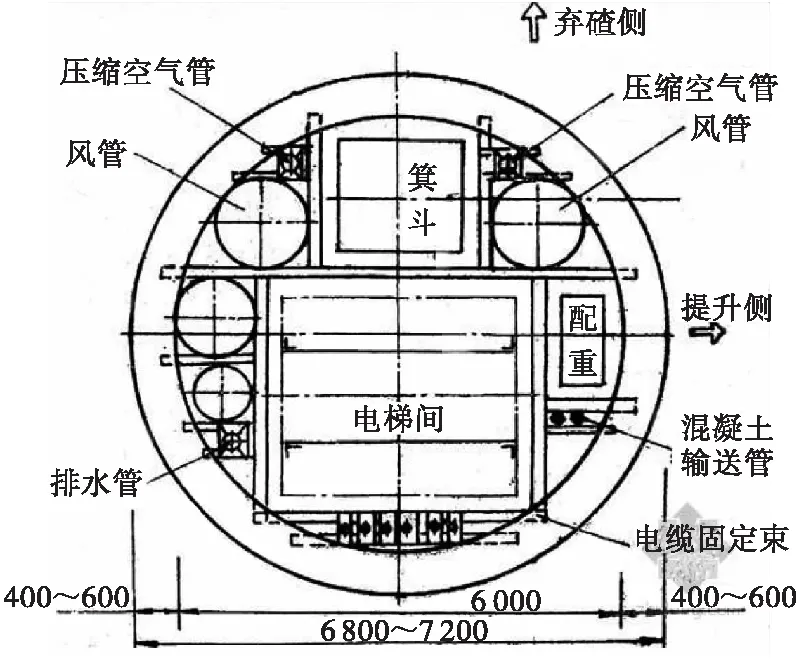
图1 新奥法施工设备断面图(mm)
该隧道上部为第四纪季覆盖土层,并混有中等风化程度的砂砾石,隧道开挖下部基岩为石炭系统的含炭灰岩,岩体整体强度普遍较高,承载能力较强,但下伏基岩受开挖爆破影响,岩体含有较多节理构造,部分岩体出现破碎,影响岩体整体强度。隧道流径内主要分布有地下水,存在于基岩上覆土层及基岩孔隙中,地下水位为25.3 m。季节降水明显,枯水季节土层中水分蒸发散尽;雨水季节,受大气降水影响,在含炭灰岩破碎带及地质构造带处会出现较少量的富水区段。隧道整体受地下水影响较弱。
2 隧道围岩应力变形特征
2.1 应力特征
隧道在开挖建设过程中,造成原有岩体应力扰动,在岩石内部孔隙重分布作用下达到平衡后,内部应力分布称之为隧道围岩应力。围岩应力一方面受岩体外部荷载及环境影响,另一方面与岩体自身构造、结构、岩体矿物成分等内在因素有关。计算围岩应力的方法较多,本文将采用谢家烋理论公式开展本工程项目隧道围岩应力计算分析。
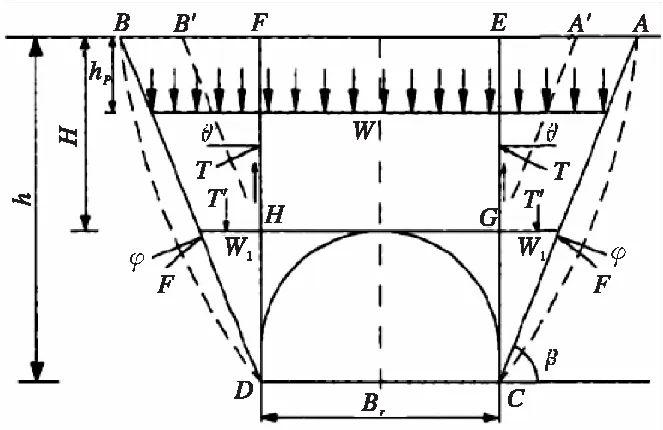
(a)隧道断面几何剖面
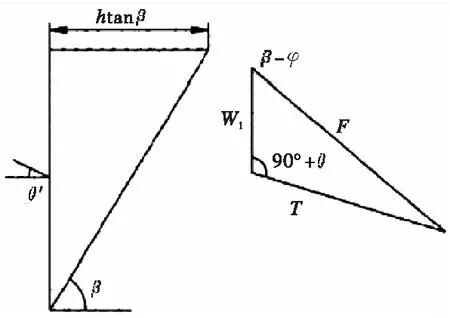
(b)计算模型图2 谢家烋理论公式简化模型图
图2为谢家烋理论公式的隧道简化模型。以洞室上端EFGH岩土层理想下滑为前提[9],但由于围岩体并不是一个理想的摩擦角滑动,需要根据具体围岩分级确定摩擦角θ。同样,此时岩土层也会受到抗摩擦力T′,阻碍EFGH的下滑,因此在洞口上端HG方向上受到的竖直压力可认为是围岩竖向压力。由岩土层理想平衡状态建立表达式,其中竖向压力为:
G=W-2T′=W-2Tsinθ
(1)
式中:W——BtγH;
Bt——隧道跨径长。
下滑阻力T与DB条岩土体有关,DB条岩土体自重可采用式(2)计算:
(2)
式中:h——计算岩土体的高度;
β——岩土材料破裂面水平向夹角。
故而得到下滑阻力T计算式为:
(3)
式中:θ——围岩体摩擦角;
φ——洞口上部岩体摩擦角。
因而,可获得岩体在滑移极限平衡状态下下滑阻力T的极大值为:
(4)
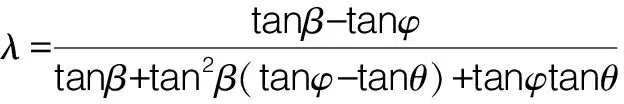
进而获得围岩竖向压力为:
G=W-γh2λtanθ
(5)
其中岩土体高度在隧道开挖过程中可近似认为与围岩顶端岩土层高度一致,故而h≈H,联立式(1)~(5)进而得到围岩竖向压力为:
G=γHBt-γλH2tanθ
(6)
最后,求得围岩体竖直应力为:
(7)
谢家烋理论公式计算模型中,水平向应力计算较为简便,采用土体力学中挡土墙压力计算理论可知:
σe=γHλ
(8)
根据地质勘察表明,本工程项目开挖隧道岩体重度为22 kN/m3,洞口宽度设计为17.2 m,隧道高度为11.33 m,隧道围岩为Ⅴ级,岩土材料参数φ=28°。当隧道围岩体为Ⅵ级时,围岩体摩擦角θ为9.8°,参照谢家烋理论公式计算模型,获得竖向应力与水平应力分别为510.387 kPa、257.28 kPa。为验证所计算的极限应力特征值的正确性,采用ABAQUS软件建立隧道围岩计算模型,共获得网格单元62 582个,节点数46 328个,按照隧道洞室特征面分为拱顶、上基准线断面与下基准线断面。在前述岩土体参数基础上,计算获得隧道围岩体竖向应力与水平应力,如图3所示。
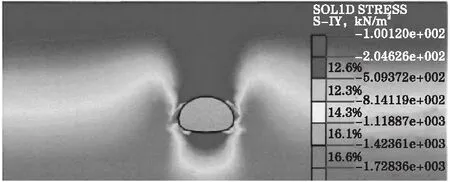
(a)竖向应力
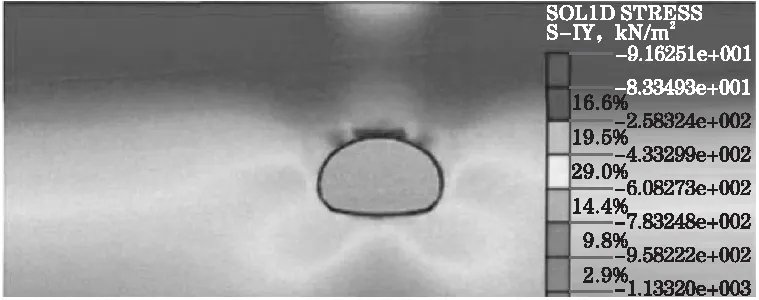
(b)水平应力图3 竖向应力与水平应力仿真计算数值解云图
从图3可看出,该隧道围岩体竖向应力最大值为509.37 kPa,水平应力最大值为258.32 kPa,两者结果与理论模型结果近乎一致,最大误差均维持在1 kPa左右,表明“横5”乐业段隧道工程围岩应力分析可采用ABAQUS数值仿真解分析。
另一方面,分析图3中应力分布特征可知,隧道围岩洞室下端应力分布区域弱于上部,隧洞下部水平应力分布为34~133 kPa,上部应力分布与之有60.5%~90.5%的差距;而竖向应力在上、下部差幅可达82.3%~1.52%倍,表明隧洞围岩竖向上应力分布受上、下工程扰动影响更大。基于围岩承载稳定性考虑,在施工过程中,围岩自身具有一定的承载强度,因而开挖过程中,可在一定程度上利用围岩洞室的自我承载力进行施工支护,节省施工锚杆的工期。
2.2 变形特征
在施工过程中设置围岩变形监测计,采集围岩变形特征值。该隧道工程开挖时间从2015-02-01开始,至2015年4月底结束第一阶段开挖。本文为分析方便,以围岩2015-02-08至2015-04-04的监测数据为分析对象。且由于变形监测计分布在隧道围岩各个区域,本文以隧道围岩断面中部变形监测计数据进行分析。
图4为采用三台阶七步法开挖施工过程中危险断面处拱顶沉降累积曲线与沉降速率曲线。从图4可看出,随着时间推移,拱顶沉降速率逐渐降低,2月13日拱顶变形速率为1.5 mm/d,而在3月5日变形速率仅为0.48 mm/d,整体上变形速率在减小。从变形速率的变化趋势来看,其经历了“三降”过程,分别发生于初始开挖、2月23日、3月10日这三个时间节点,与三台阶施工进度相一致,这表明每一次台阶开挖都会导致拱顶变形速率下降。自3月20日以后,即施工40 d后,拱顶沉降速率逐渐降低至0 mm/d,沉降量累计值也逐渐达到饱和值154 mm,全过程变形分布为20~154 mm,在开挖30 d之后,沉降量累计值已达到150 mm,占最终沉降量饱和值的90.3%,表明该隧道围岩拱顶沉降变形主要集中在施工前1个月内。基于最小二乘法拟合出拱顶沉降量累计曲线与时间的幂函数关系,其表达式如下:
y=170.47-187.18×0.75x
(9)
式中:y——累计变形;
x——施工时间。
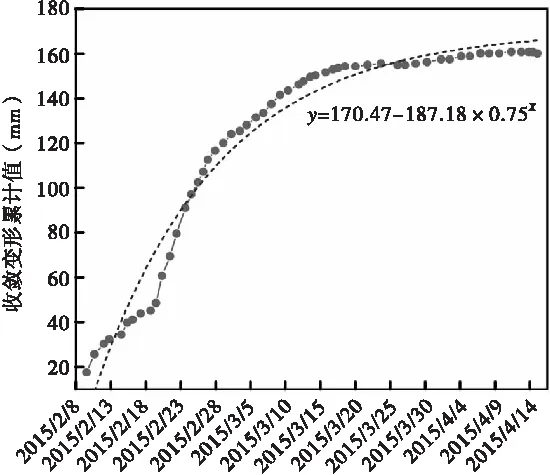
(a)累计变形
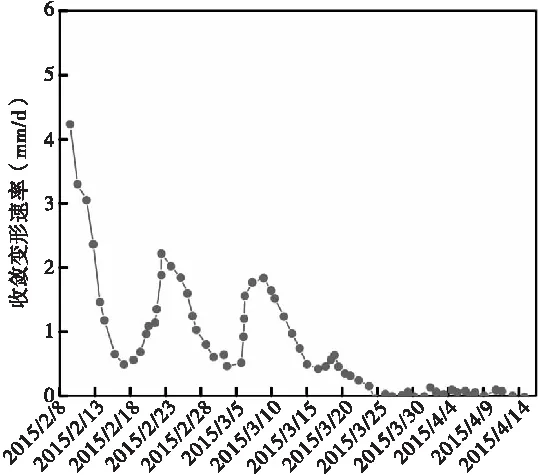
(b)变形速率图4 拱顶沉降累计值曲线与沉降速率曲线图
图5为隧道围岩断面中部处上、下基准线变形收敛曲线。从图中隧道围岩上基准线收敛变形曲线可看出,上基准线收敛速率可分为三个阶段:在施工开挖前10 d,基准线收敛速率逐渐降低至0.2 mm/d,基准线收敛值逐渐增加,增加量达6 mm,该阶段内收敛变形值占整个上基准线总变形的47.7%;在施工开挖第10~35 d,基准线收敛速率产生较大波动性,最大和最小变形速率差距可达0.75 mm/d,该阶段内基准线收敛累计值上升趋势也较为缓慢,该过程维持25 d,但收敛值仅增长了6 mm;施工第35 d后,上基准线收敛值逐渐趋于稳定,收敛速率也趋近于零。综合分析可知,断面上基准线变形速率在第二台阶开挖时会出现局部速率波动式振幅变化,但其变形速率处于可控状态,累计变形并未超过安全允许值。
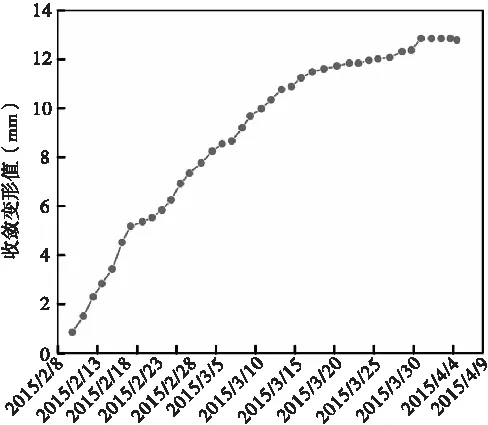
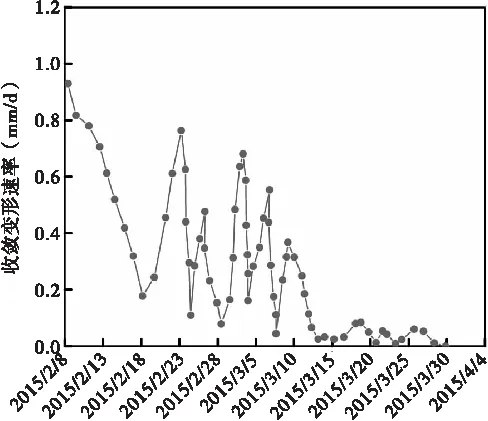
(a)上基准线
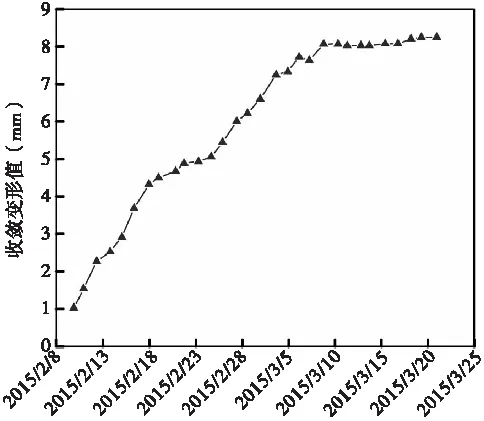
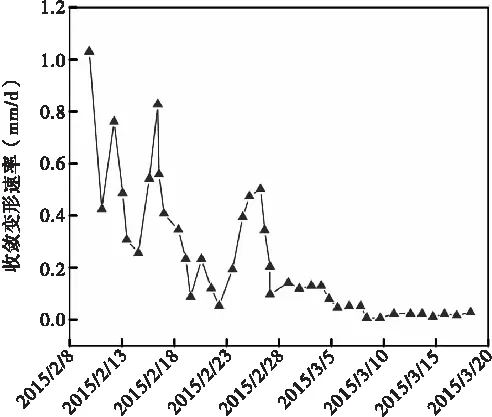
(b)下基准线图5 上、下基准线收敛变形及变形速率曲线图
从图5隧道围岩下基准线收敛速率曲线可看出,从施工开挖至3月5日,收敛速率呈波动性,但整体速率放缓,收敛累计值达8 mm,该过程累计值占总下基准线饱和收敛变形值的98%。在此之后,下基准线收敛变形呈饱和状态,收敛速率趋于零。对比上、下基准线断面上的收敛累计变形差异可知,在三台阶施工全周期内,下基准线累计收敛变形分布为1~8.35 mm,累计最大收敛变形值较上基准线处最大变形值减少了35.8%,且在三台阶施工各阶段中收敛变形值均低于上基准线断面。相比之下,下基准线上收敛变形速率与上基准线基本一致,表明隧道断面基准线上的变形速率与方向一致,不受上、下基准线影响,但由于上、下基准线处围岩变形差异,导致两者差异体现在变形累计值。
图6为典型断面处拱顶、上基准线、下基准线在特征时间点时的变形量占比。在同一特征时间点下,拱顶变形累计量占比最低,而下基准线收敛变形累计占比高于上基准线。施工第10 d时,下基准线收敛变形占比已达到其总变形的60%,而拱顶、上基准线的收敛变形还未过半,表明同一断面处不同部位的收敛变形具有阶段性变化差异。在施工开挖20~25 d时,下基准线处收敛累计变形达到饱和状态,而拱顶、上基准线分别在第40 d、35 d左右才达到饱和状态,由此表明在施工开挖过程中,拱顶面及上、下基准线施工工序可以此作为优化。
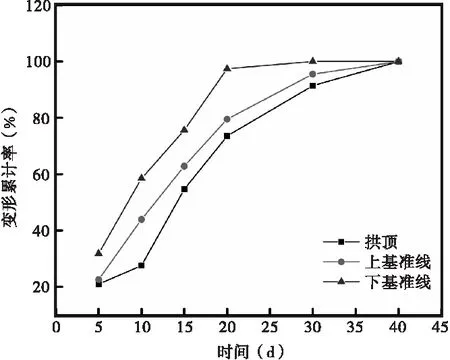
图6 典型断面不同区域变形累计量占比曲线图
3 隧道施工工艺优化探讨
根据该隧道围岩应力与变形特征值,考虑采用三台阶八步法施工工艺[10]。其中,根据前文应力与变形特征分析知,开挖过程中需要注意台阶宽度与拱顶变形值,因而设计施工工艺流程如图7所示。
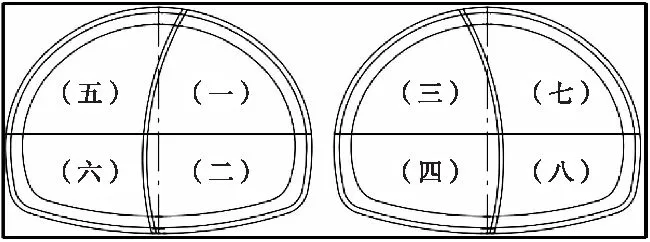
图7 隧道施工优化工序流程图
为此,采用ABAQUS仿真平台对三台阶八步法施工工艺优化后的隧道断面收敛累计变形值进行计算,以断面拱顶处变形为分析对象,如图8所示。
从图8(b)中可知,由于施工工艺仍是三台阶法施工,因而拱顶上收敛变形速率仍呈“三阶段”变化特征,但各阶段变形速率持续时间有所缩短;另一方面,收敛累计变形值与时间参数仍具有幂函数关系。第一阶段中变形速率下降最快,持续6 d,该阶段最终变形速率为0.5 mm/d,收敛累计变形达26 mm,占拱顶全施工周期内变形量的27.6%。相比之下,第二阶段中收敛变形速率较小,为0.5~2.2 mm/d,持续时间为7 d,累计变形增长量为62 mm,该阶段内所达到的收敛累计变形占总体变形量的66%。第三阶段中变形速率较稳定,最大变形速率为1.33 mm/d,累计收敛变形基本达到最大值,处于较“饱和”状态。相比七步法施工,八步法施工工艺下拱顶上收敛累计最大变形值为94 mm,较前者减少了41.4%。且该施工工艺下各个台阶工法施工后,拱顶变形具有稳定期,有利于洞室支护施工;另一方面,变形速率波动幅度较小,收敛累计变形在第20~25 d达到稳定状态,对台阶法工期控制具有正面作用。
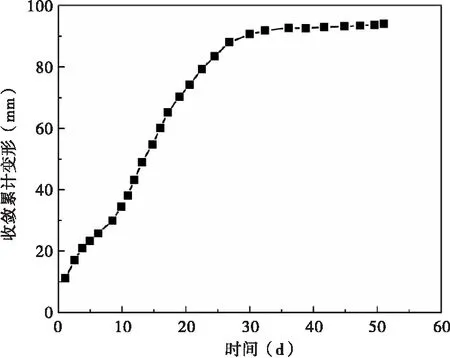
(a)累计变形
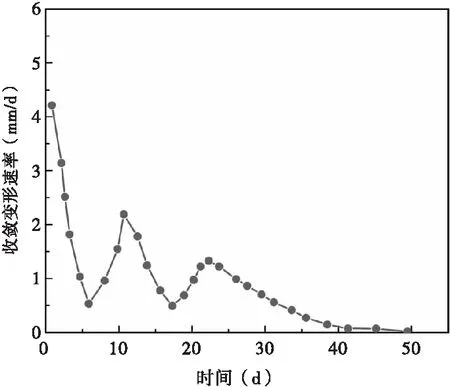
(b)变形速率图8 拱顶累计变形与变形速率曲线图(三台阶八步法)
4 结语
(1)本文基于理论模型计算与数值模拟两种手段,获得隧道围岩理论模型与数值模拟结果的应力特征值基本一致,围岩竖向应力与水平应力最大分别为509.37 kPa、258.32 kPa,且洞室下部应力弱于上部。
(2)三台阶七步法施工工艺下,拱顶变形集中在1个月内,变形速率为递减;下基准线变形累计值低于上基准线,但收敛变形速率与上基准线基本一致;同一特征时间点,拱顶变形累计量占比最低。
(3)三台阶八步法施工工艺优化后,拱顶变形稳定性较好,在第20~25 d达到稳定状态,收敛变形累计最大值较七步法减少了41.4%,有利于控制隧道断面变形与施工周期。
