When null energy condition meets ADM mass
2022-10-22RunQiuYangLiLiandRongGenCai
Run-Qiu Yang,Li Li and Rong-Gen Cai
1 Center for Joint Quantum Studies and Department of Physics,School of Science,Tianjin University,Yaguan Road 135,Jinnan District,Tianjin 300350,China
2 CAS Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China
3 School of Fundamental Physics and Mathematical Sciences,Hangzhou Institute for Advanced Study,UCAS,Hangzhou 310024,China
Abstract We give a conjecture on the lower bound of the ADM mass M by using the null energy condition.The conjecture includes a Penrose-like inequality 3M≥and the Penrose inequalitywithA the event horizon area and к the surface gravity.Both the conjecture in the static spherically symmetric case and the Penrose inequality for a dynamical spacetime with spherical symmetry are proved by imposing the null energy condition.We then generalize the conjecture to a general dynamical spacetime.Our results raise a new challenge for the famous unsettled question in general relativity: in what general case can the null energy condition replace other energy conditions to ensure the Penrose inequality?
Keywords: Penrose inequality,black holes,ADM mass,energy conditions
1.Motivation
It is still an open and interesting question on the bound of mass in a given region of spacetime.The Penrose inequality provides a lower bound for the mass of spacetime in terms of the area of suitable surfaces that typically represent black holes.More precisely,Penrose’s motivation for his inequality is as follows.Suppose one begins with asymptotically flat initial data with the ADM mass M,and the apparent horizon σ with A[σ]the minimum area required to enclose σ.Evolving the system forward in time and supposing that the spacetime eventually settles down to a Kerr solution with its Bondi mass Mfand the area of the event horizon Af,one immediately finds 2Mf≥(in units of 16πG=c=1).Considering the null energy condition (NEC),the Bondi mass does not increase,while the area of the event/apparent horizon does not decrease,i.e.M≥MfandAf≥A[σ].Therefore,one obtains the ‘Penrose inequality’ 2M≥The Penrose inequality is important to gravitational collapse and the cosmic censorship conjecture.Nevertheless,finding the proof for this inequality is still a famous open problem in general relativity.In the special case that the spacetime is static,the inequality was proved by various methods assuming weak energy condition (WEC) [1–7](see [8]for a review).For the dynamical case,the only known proof was given for the spherically symmetric spacetime by considering the dominant energy condition (DEC) and using ‘ADM energy’instead of ADM mass[8,9].However,there are two obvious ‘gaps’: (1) only the NEC is involved in Penrose’s heuristic argument,but the current statement of the Penrose inequality requires WEC or even DEC,and(2)the spacetime is assumed to settle down to a stationary black hole in Penrose’s argument,but this assumption plays no role in current studies and proofs.Moreover,note that the ‘positive mass theorem’ is a corollary of Penrose inequality and [10–12]showed that the NEC can indeed insure nonnegative ADM mass.These raise an interesting question:if assuming that the spacetime will settle down to a stationary black hole finally,is it able to prove the Penrose inequality by using the NEC only? On the other hand,the surface gravity к and event horizon areaA are two important quantities of black holes.If taking both into account,can we obtain a new lower bound on the ADM mass?
To answer these questions,we first consider the Kerr–Newman black hole with ADM mass M,angular momentum Ma,charge Q.We then have
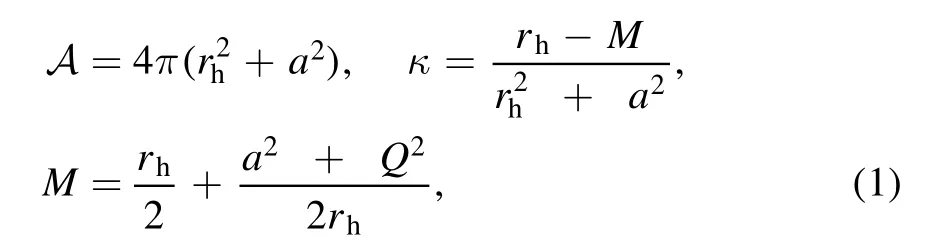
with rhthe location of the event horizon.We can obtain that

and the saturation appears only if a=Q=0.Based on the above discussions,we propose a conjecture as follows.
Conjecture 1.For a four-dimensional asymptotically flat,static or axisymmetric stationary black hole with ‘t-φ’reflection isometry,if(1)Einstein’s equation and the NEC are satisfied and (2) the cross-section of event horizon has S2topology,then there are two independent inequalities given as follows:

and the Penrose inequality

The equality is achieved only when the exterior of a black hole is Schwarzschild.Moreover,a regular stationary spacetime that is singularity free satisfiesM≥0 and M vanishes only for the Minkowski spacetime.
Here we make some comments before going further.Firstly,the event horizon in Conjecture 1 is a Killing horizon for which the surface gravity к is well-defined.We note that the event horizon of a stationary black hole is not guaranteed to be a Killing horizon.According to Hawking and Ellis [13],when Einstein’s equation holds with matter satisfying suitable hyperbolic equations and the DEC,the event horizon of a stationary black hole is a Killing horizon.However,here we only use the NEC.Instead,Carter proved that for a static or axisymmetric stationary black hole with ‘t-φ’ reflection isometry,the event horizon is a Killing horizon and the surface gravity is a constant,regardless of Einstein’s equation and energy conditions [14].Secondly,the surface gravity к depends on the normalization of the Killing vector ξμ.This can be fixed by requiring ξμtμ|∞=-1,where tμis the tangent vector of the world-line of static observers at infinity.Thirdly,our inequality(3) and Penrose inequality(4)are two independent inequalities in general if we do not require other stronger energy conditions.In static case,if the strong energy condition is also imposed,one can use Komar integration to prove M≥кA/4π and find that the inequality(3)is a corollary of Penrose inequality.Since we here only impose NEC,it is possible that the strong energy condition is violated everywhere .In this situation one can find that M<кA/4π and the Penrose inequality becomes a corollary of inequality(3).Finally,our conjecture contains a ‘positive mass theorem’ as its corollary.Though we assume static or axisymmetric stationary symmetry,we only use NEC rather than DEC or WEC.If a spacetime satisfies the NEC while breaking the WEC,the scalar curvature of the maximal slice can be negative.Then the proofs proposed by Schoen and Yau[15,16]and various generalizations will lose their validity.The proofs based on spinor technique,originally proposed by Witten[17,18](see also the extension to black holes[19]),require the DEC to ensure the nonnegativity of energy integration,thus would lose their validity for a spacetime that satisfies the NEC only.Compared with the results of [10,11],which used the NEC to prove the nonnegativity of ADM mass,our paper offers a tighter lower bound for the ADM mass in terms of к andA.Moreover,if the WEC is broken,all proofs till now about the Penrose inequality will become invalid.
2.Proof in static spherically symmetric case
It is clear that the Kerr–Newman black hole satisfies our Conjecture 1.To further support our inequalities in Conjecture 1,we now give proof for the static spherically symmetric case for which the metric reads

The asymptotic flatness yields

with M the ADM mass and the constant α >0.For a black hole,we donate the location of its event horizon to be rhat which f(r) is vanishing,then the surface gravity к and the horizon areaA are given by
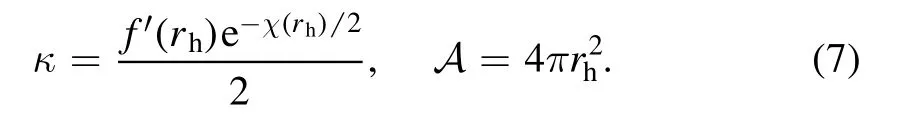
For a regular case that is singularity free,both f and χ are smooth at r=0.The energy momentum tensorTμνhas a formTμν=diag [-ρ(r),pr(r),pT(r),pT(r)].Einstein’s equation gives the following independent equations

We note that the NEC insuresχ′≤0.Therefore,we find from(6) that χ≥0.
To prove the inequalities(3) and(4) for the spherically symmetric case,we introduce a new‘quasi-local mass’for an equal-r surface defined as
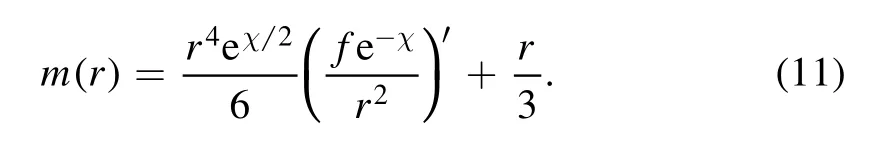
Using equations (8)–(10),one can obtain that

It is now manifest that the NEC insuresm′(r)≥0 outside rh.Evaluating m(r)at both the infinity and the event horizon,one finds

so inequality(3) follows.If the spacetime is regular,i.e.horizonless and all curvature invariants are regular everywhere ,we have M=m(∞)≥m(0)=0.
Next,we prove the Penrose inequality(4).Solving f(r)e-χ(r)/r2in terms of m(r),one obtains from(12) that

Evaluating(14)at r→∞and noting that 3m(r)-r≤3M-r under the NEC,one has
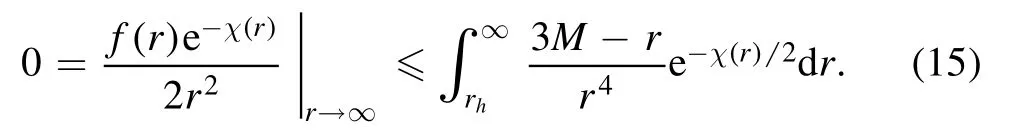
Monotonicity of e-χ(r)/2ensures

which leads to

I nequality(15) then implies
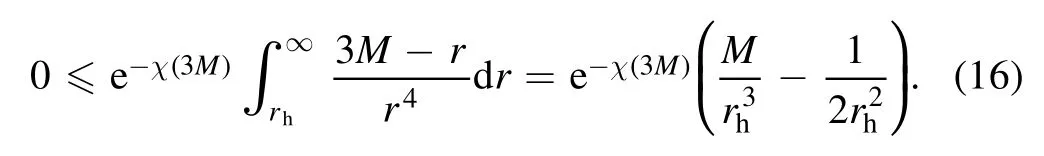
One immediately finds 2M≥rh,and therefore the inequality(4) follows.
To prove the rigidity for both inequalities(3)and(4),we note that they are saturated only if χ(r)=0 and m(r)=M.This leads to f(r)=1-2M/r,i.e.the Schwarzschild spacetime.Moreover,a regular stationary spacetime satisfies M≥0 and M vanishes only for the Minkowski spacetime.
Note that the Penrose inequality of dynamical spacetime was proved in the spherically symmetric case by considering the DEC and the ADM energy in the literature [8,9].Interestingly,our proof for the spherically symmetric case implies the following corollary,
Corollary1.Consider a dynamical spacetime that has spherical symmetry and settles down to a static black hole finally.For an initial data set containing an apparent horizonσ,the NEC and Einstein’s equation guarantee 2M≥where A[σ]is the minimum area required to enclose the apparent horizonσ.The proof is as follows.Based on proposition 9.2.1 of[13],if the initial data set contains an apparat horizon σ and the NEC is satisfied,there must be an event horizon H and the apparent horizon lies behind H.We denote the intersection of H and the initial data set as Γ0,so σ must be inside Γ0.Since A[σ]is the minimum area required to enclose the apparent horizon,one has A[σ]≤ A(Γ0).The NEC ensures that the area of the event horizon is nondecreasing,so we haveA(Γ0)≤A∞,where A∞is the event horizon area at the future timelike infinity.Moreover,the mass of the final black hole is given by the Bondi mass MB.Note that we have proved the Penrose inequality for a static black hole with spherical symmetry.Therefore,we have

where we have used the fact that the Bondi mass is equal or smaller than the ADM mass.Corollary 1 shows that in a spherically symmetric case,the NEC is enough to ensure the Penrose inequality,the same as Penrose’s heuristic argument.Compared to previous proofs in the spherically symmetric case [8],we have a natural requirement that the system will finally settle down to a static black hole.Nevertheless,our result is stronger in the following two aspects: we use the ADM mass rather than the ADM energy,and we use the NEC rather than the DEC.We also stress that A[σ]is not defined by the area of the apparent horizon σ.As pointed out by[20],the apparent horizon area,in general,may not satisfy the Penrose inequality.
3.Generalization to dynamical black holes
To generalize Conjecture 1 to the dynamical case,we should first clarify two conceptions in a non-stationary black hole:the ‘horizon’ and the ‘surface gravity’.Two possible candidates for the horizon in the dynamical case are the ‘future outer trapping horizon’ (FOTH) introduced by Hayward [21]and the‘dynamical horizon’(DH)proposed by Ashtekar[22].In this paper,we will take the former.
The definition of the ‘surface gravity’ in the dynamic spacetime is also a subtle issue.Once again,one has two potential choices,the‘trapped gravity’proposed by Hayward[21]and the ‘effective surface gravity’ by Ashtekar [22],respectively.However,both of them cannot reduce to the surface gravity even in the static spherically symmetric case,equation (7).We now propose a new candidate of surface gravity as follows.Near the null infinities{I-,I+} and spatial infinity i0,there is an asymptotically time-like Killing vector tμwhich stands for the 4-velocity of a static observer.Take lμand kμto be,respectively,the infalling and outgoing null vectors of a FOTH.We can extend them into the whole spacetime by requiring that: (1) they are tangent vectors of null geodesics,(2) lμis affinely parameterized and satisfies lμtμ=-1 at {I-,I+,i0},(3) kμis normalized by requiring kμlμ=-1 everywhere .Then,according to the null vector fields {lμ,kμ} and their expansions {θ(l),θ(k)},our ‘surface gravity’ is defined as

The surface gravity defined in this way is always nonnegative and will reduce to equation (7) in the static spherically symmetric case.
We now generalize Conjecture 1 to the dynamical case as follows.
Conjecture 2.For the most outer FOTH which coincides with the event horizon at the future timelike infinity,if (1)Einstein’s equation and the NEC are satisfied,and (2) all marginal trapped surfaces of the FOTH have spherical topology,then the areaA of a marginal trapped surfaceS,the surface gravity к,and the ADM mass of spacetime will satisfy

and

If it is saturated on one marginal surface of FOTH,then the FOTH is the event horizon,and the exterior of the event horizon is Schwarzschild.
It has been proved in [21]that the area of marginal surface of FOTH is nondecreasing.Therefore,one can find that inequality(19) is a corollary of(4) in Conjecture 1.
We now give a nontrivial check for the inequality(18)by considering the generalized Vaidya solution [23]:

Note that the ADM mass M is defined at the spatial infinity,i.e.M=M(∞,∞).The marginal trapped surfaces are given byv=const.andr=const.,thanks to the spherical symmetry.Then the infalling and outgoing null rays are,respectively,lμ=(0,-1,0,0) and kμ=(1,f/2,0,0) with their expansions θ(k)=f/r and θ(l)=-2/r<0.Therefore,the FOTH is given by f(v,r)=0 for which we denote its solution to be r=rh(v).We then have

from which

The corresponding energy–momentum tensor reads [24]

with

This in general (u ≠0) describes the Type II fluids [13].The NEC demands
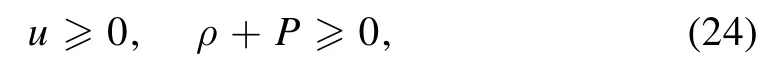
as well as the following constraint onM(v,r)

so the inequality(18) follows.To saturate the inequality,we needM(v,r) to be a constant,so the exterior is nothing but Schwarzschild.This provides nontrivial evidence to support our Conjecture 2.Note that,in the present case,the WEC requires {u≥0,ρ≥0,P≥0} and the DEC gives {u≥0,ρ≥P≥0},both are stronger than the NEC.
4.Summary
To summarize,we have proposed a Penrose-like inequality involving ADM mass,surface gravity,and horizon area.For static or axisymmetric stationary black holes,our Conjecture 1 suggests that Einstein’s equation and the NEC ensure the Penrose-like inequality as well as the Penrose inequality.We have given a proof for the static spherically symmetric case and offered evidence for the dynamical case.In addition,the Penrose inequality for spherically symmetric(dynamic) spacetime has been proved by using the NEC rather than the DEC.Our conjecture applies in some situations not covered by previous inequalities.
Our results not only provide a new conjecture to bound the ADM mass by horizon area and surface gravity for the first time,but also raise a new challenge for the famous unsettled question in general relativity: can the NEC ensure the Penrose inequality if a spacetime settles down to a stationary black hole finally?
Acknowledgments
This work was partially supported by the National Natural Science Foundation of China Grants No.12122513,No.12075298,No.11821505,No.11991052,No.12047503,and No.12005155,and by the Key Research Program of the Chinese Academy of Sciences(CAS)Grant No.XDPB15,the CAS Project for Young Scientists in Basic Research YSBR-006 and the Key Research Program of Frontier Sciences of CAS.
杂志排行
Communications in Theoretical Physics的其它文章
- Preface
- Phase behaviors of ionic liquids attributed to the dual ionic and organic nature
- Chaotic shadows of black holes: a short review
- QCD at finite temperature and density within the fRG approach: an overview
- The Gamow shell model with realistic interactions: a theoretical framework for ab initio nuclear structure at drip-lines
- Effects of the tensor force on low-energy heavy-ion fusion reactions: a mini review
