High precision solutions to quantized vortices within Gross–Pitaevskii equation
2022-10-22HaoHaoPengJianDengSenYueLouandQunWang
Hao-Hao Peng,Jian Deng,Sen-Yue Louand Qun Wang
1 Department of Modern Physics,University of Science and Technology of China,Hefei,Anhui 230026,China
2 Institute of Frontier and Interdisciplinary Science,Key Laboratory of Particle Physics and Particle Irradiation (MOE),Shandong University,Qingdao,Shandong 266237,China
3 School of Physical Science and Technology,Ningbo University,Ningbo 315211,China
Abstract The dynamics of vortices in Bose–Einstein condensates of dilute cold atoms can be well formulated by Gross–Pitaevskii equation.To better understand the properties of vortices,a systematic method to solve the nonlinear differential equation for the vortex to very high precision is proposed.Through two-point Padé approximants,these solutions are presented in terms of simple rational functions,which can be used in the simulation of vortex dynamics.The precision of the solutions is sensitive to the connecting parameter and the truncation orders.It can be improved significantly with a reasonable extension in the order of rational functions.The errors of the solutions and the limitation of two-point Padé approximants are discussed.This investigation may shed light on the exact solution to the nonlinear vortex equation.
Keywords: quantum vortex,Gross–Pitaevskii equation,two-point Padé approximants
1.Introduction
Vortices are strongly nonlinear excitations in superfluids,which are quantized as topologic defects from the long range quantum phase coherence [1–3].The formation,stability and dynamical properties of vortices have been intensively studied experimentally [4–8]and theoretically [9,10].Vortices play important roles not only in many-body quantum systems,but also in dark matter[11–13]and the phase transition of the early universe [14–17].The structure of nonlinear dynamics for vortices is in connection with the gravitational field equation for the metric of black holes,which makes it possible to study the Penrose process of rotating black holes in laboratories [18,19].Vortices are also necessary degrees of freedom in turbulence and the intermediate state of an overpopulated off-equilibrium system.The generation and clustering of vortices and the annihilation of vortex–antivortex pairs are closely related to the scaling law of a non-thermal fixed point [20–26].
The static and dynamical properties of vortices and vortex lattices at zero temperature limit can be well described by the Gross–Pitaevskii equation (GPE),which is a nonlinear Schrödinger equation with the nonlinearity being determined by interactions through a mean-field approximation [27,28].This equation emerges in various nonlinear phenomena,and has been extensively studied in connection with nonlinear optics,plasma physics and fluid dynamics.The GPE helps the prediction and description on experimental observations of nonlinear effects,such as vortices and interaction among them [29,30].
As an individual object,the vortex has an internal structure and can also be involved in an external evolution.How the wave function of a vortex responds to a perturbation or to the nonuniformity of the condensate is an interesting and complicated problem.The structure of the vortex core is determined by the properties of the vortex itself,but it should also match the outer wave function determined by the collective motion and interaction with the environment.Through a unique coordinate transform and matching the asymptotic expansion inside and outside the vortex core,a set of differential equations have been derived to describe the overall structure and collective motion of the vortex in a perturbative way [31,32].
To construct a perturbation theory,the ideal starting point is a system with an exact solution.If the disturbance is not large,a series of perturbative solutions can be obtained systematically,so that a reliable understanding of the complex system can be achieved.The various physical quantities associated with the perturbed system can be expressed as corrections to the original one.For example,the contribution from the trace anomaly of the QED energy momentum tensor to the mass of the hydrogen atom,the simplest QED bound state,is calculated in[33],where the Lamb shift from the vacuum polarization and radiative corrections to the electron mass are perturbative corrections to the ground state with an exact wave function.
To study the vortex dynamics in a perturbative way,the stationary wave function of a vortex in a uniform condensate is the starting point.But due to the nonlinear nature of this problem,an exact solution to the nonlinear ordinary differential equations(ODE)has not been found yet.The best alternative we can think of is to look for an approximate function that is simple,compact and as precise as possible.This can be done with the method of two-point Padé approximants.The basic idea of Padé approximants is to construct a rational function which can reproduce the Taylor expansion series of the target function within a given order.The rational function can mimic the singularity of the target function since it contains pole structure,so the convergence radius of the original Taylor expansion can be extended (see an example in [34]).If the target function is constrained by two boundary conditions,the rational function should reproduce two Taylor expansion series simultaneously,which is called twopoint Padé approximants[35,36].We found that this scheme is particularly suitable for finding approximate solutions to the nonlinear equation for the vortex.The main purpose of this paper is to explore the precision limit of this scheme,hoping to provide a clue for the exact solution of the vortex.
The outline of this paper is as follows.In section 2,the static and rotationally symmetric equation for the voetex is derived.In section 3,a very high precision numerical solution to the vortex equation is obtained with a relaxation method,which can be used to test the accuracy of the approximate solutions.In section 4,the results from two-point Padé approximants are presented.In section 5,the errors and challenge of this approach are discussed.The conclusions and discussions are given in section 6.
2.Vortices within GPE
The Bose–Einstein condensate(BEC)in cold atom systems at zero temperature can be well described by the Gross–Pitaevskii (GP) theory as the mean-filed approximation of quantum field theories[1].In GP theory,the ground state and weakly excited states of the condensate are described by the complex wave function ψ(r,t),which satisfies GPE,
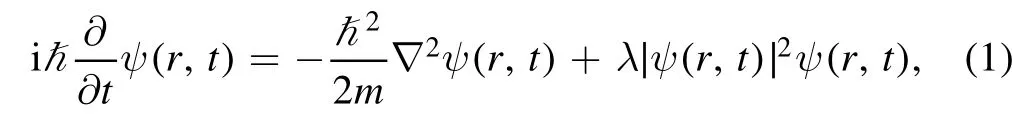
where ħ is the reduced Planck constant,m is the particle mass,and the coupling constant λ can reproduce the s-wave scattering length,λ=4πasħ2/m in the Born approximation.The investigation on the exact and numerical solutions to GPE improves our understanding on the nonlinear dynamics of matter waves in BEC [30].In this work,we will focus on the static and rotationally symmetric solution to GPE,the quantum vortex,a kind of topological excitation in a superfluid in presence of the local orbital angular momentum.The wave function can be written in the following form
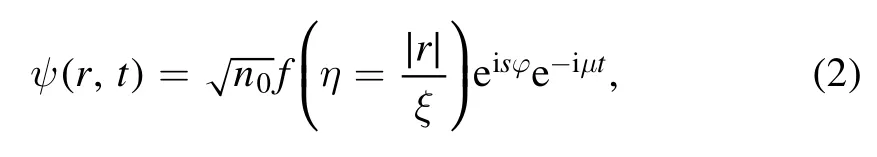
where n0is the bulk number density,is the healing length,φ is the azimuthal angle,μ is the chemical potential,s is the winding number which must be an integer to keep the wave function single-valued.The normalized amplitude function f(η) satisfies the nonlinear ordinary differential equation (ODE)
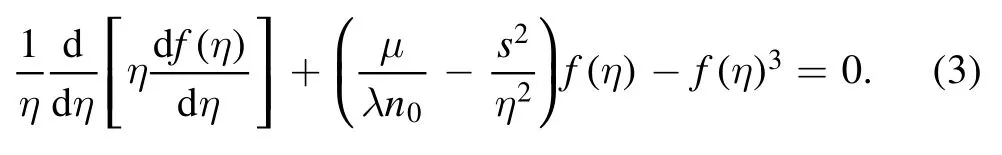
Physically,the area modified by a vortex is rather limited,the density profile should return to the bulk value in a region far away from the vortex core,which requires μ/λn0=1.So the ODE can be put into the form
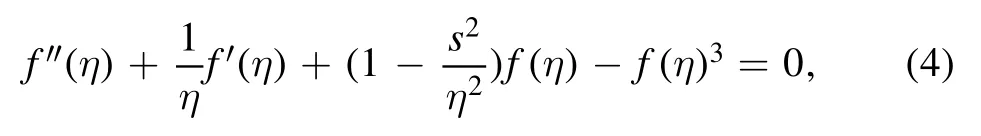
with the boundary conditions f(η→0)=ksηsand f(η→∞)=1.Here ksis the connecting parameter,which plays an important role in the vortex solution.
The purpose of this work is to solve equation (4).Without the cubic term,the ODE becomes Bessel’s differential equation with Bessel functions as the formal solution,but the boundary condition at infinity cannot be satisfied.With the cubic term,however,the equation is a nonlinear ODE.It is very hard,if not impossible,to obtain the exact analytical solution to it.So far,we can only find a similar example with an exact solution.It can be easily checked thatf=tanh(η) is one solution to the nonlinear ODE,f″+f(1-f2)=0 with the same boundary conditions.This solution is a direct extension of the Riccati equation.In appendix A,we will demonstrate another way to obtain this exact solution which may provide some hints for solving equation (4).The example gives us a little hope that a sufficiently precise numerical solution can guide the guesswork about the possible form of the analytical solution.
For the numerical solution,the differential equation with two-point boundary conditions can be solved with shooting method,which requires a fine tuning of ksto achieve the right limit f(η→ηC)→1 andf′ (η→ηC)→0in the range η<ηC.The shooting results of f(η) for the winding numbers s=1,2,3 are shown in figure 1.It seems that shooting works well,but the results are not stable for a large ηC,because a rigorous precision in ksand an inaccessible small step size in the finite difference are required.Fortunately,we find a relaxation method which can achieve a very high precision in the whole region of 0<η<∞.The technical details will be discussed in the next section.
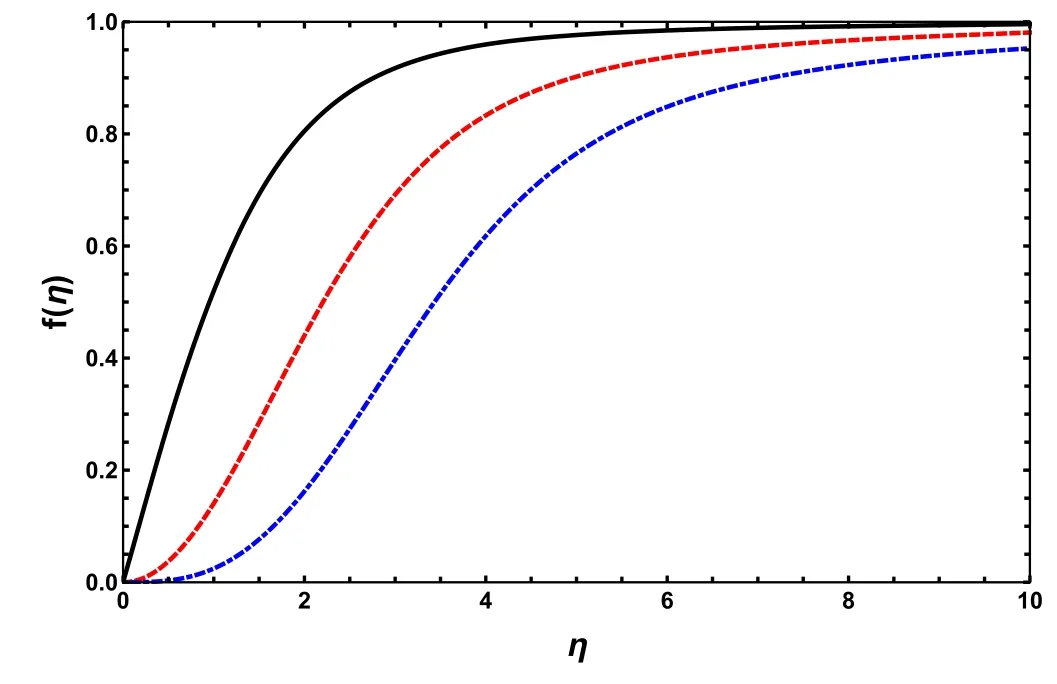
Figure 1.The profile function f(η) are obtained with shooting method in the range η<ηC=10.Black solid line,red dashed line and blue dash-dotted line stand for the results with s=1,2,3 respectively.
3.Relaxation iteration for a high precision numerical solution
A high precision numerical solution to equation (4) can be achieved by a relaxation iteration.The method is built up with three steps.Firstly,we take a replacement for the target function,f(η)→ηs/(ηs+1)+h(η).The auxiliary function ηs/(ηs+1)is to make the unknown function h(η) satisfy the boundary condition h(0)=h(∞)=0,which is convenient for solving the ODE.The function h(η) satisfies the nonlinear ODE as follows
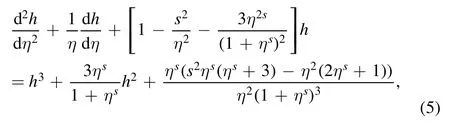
where we have put all linear terms of h(x)to the left-hand-side.Secondly,we replace the variable to x=η/(R+η),so that the limit η→∞is shifted to x→1.The positive number R sets a finite scale,we choose R=1 without loss of generality.The nontrivial change is
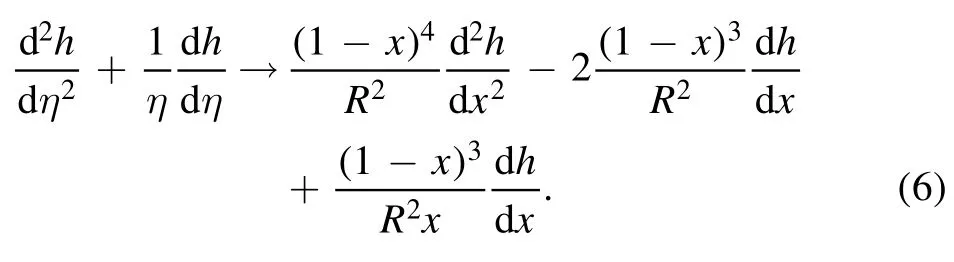
In this way,the ODE is ready for the discretization and iteration.
Finally we discretize x as xi=iΔx,where i=0,…,N and the step size is Δx=1/N.So the derivatives become
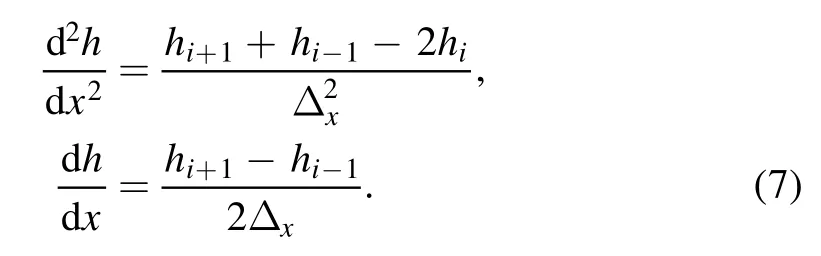
Then the nonlinear ODE is changed to a set of linear algebraic equation

for i=1,…,N-1,where ai,bi,ci,wi(hi)are well defined at each point.Because of the well-designed boundary condition,h0=hN=0 does not interfere with the iteration,then equation (8) can be rewritten as

We may start by choosing a set of reasonable values for hiand obtain wi(hi),then a new set of hican be determined by solving the tridiagonal algebraic equation (9).In this way,a high precision solution can be achieved within dozens of iterations.In the last iteration,the maximum error to hiis smaller than 10-25,which means that the algorithm has a fast speed of convergence.The main source to the error comes from the discretization,which can be improved by increasing the number of points N.We find the maximum difference between the results with N=225and N=226is of the order 10-16,which sets the precision of our numerical solution.The main challenge to go beyond larger N is to handle a larger dimension vector with high precision on a personal computer,that is the reason we stopped at N=226.For the vector with such a dimension,the iteration to achieve the required precision can be done in a few hours.
For applications,the numerical solution in the form of data sample is not convenient.It is better to look for an approximate analytical solution.The present numerical solution can be used to verify the accuracy of the approximate analytical solution.
The most important input for the approximate analytical solution is the value of connecting parameter ks.We can get it from the numerical solution in the following way.To determineks=with a higher precision,the behavior of f(η) near η=0 can be parameterized by
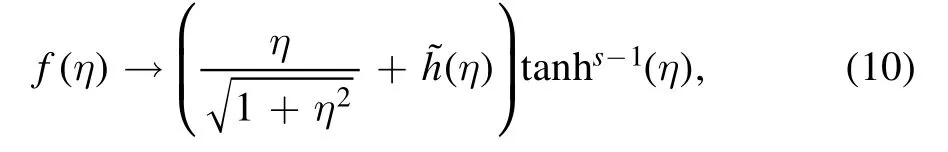
for example,for winding number s=1,we find that f(η)/η can be best fitted by RN(1-η2/8)for small η,where RNis the fitting parameter corresponding to the solution with N grid points.The left panel in figure 2 shows the numerical result for f(η)/η-RNwith N=226.The dependence of RNon N is in table 1 and visualized in the right panel of figure 2.
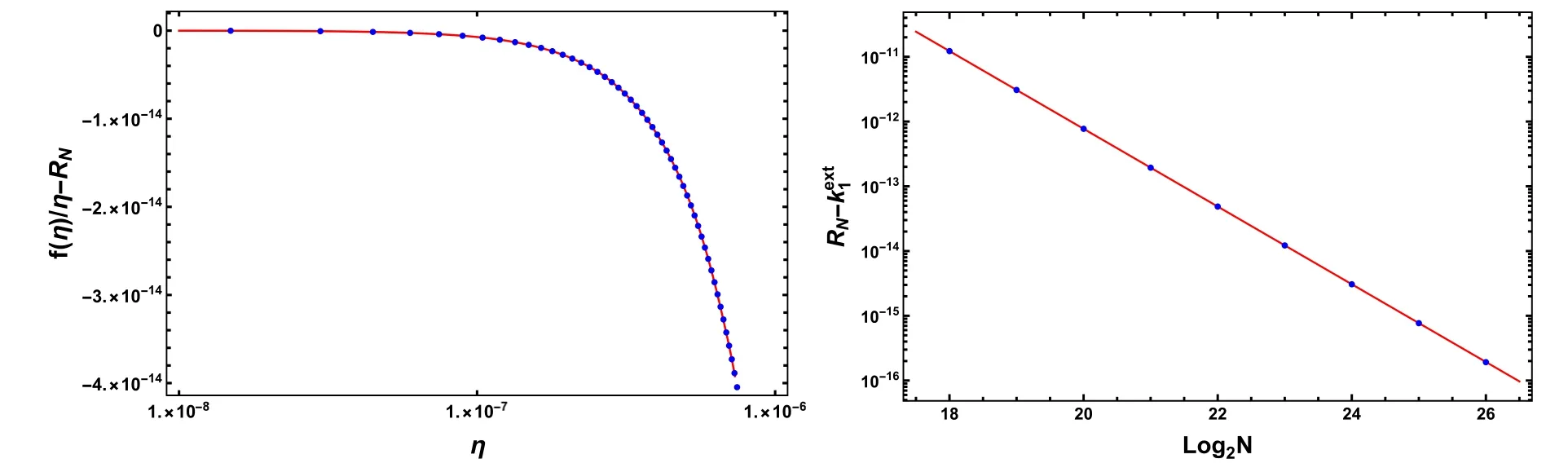
Figure 2.Left: numerical results for f(η)/η-RN with N=226.Right: numerical results for RN-k1ext=βγlog2N as a function oflog2 N.
We may extract the valuek1=limN→∞RNby an extrapolation because these points can be best fitted in the formRN-k1ext=βγlog2Nwith fitting parametersk1ext,β and γ.Thenk1extcan be regarded as a high-precision approximation to the exact value of k1.Its reliability will be discussed in the following sections.
In the same way,the extrapolated values of ksfor s=2,3 can be obtained

The precision of the connecting parameters is reduced for larger s,because it is harder to extract the small η behavior of f(η)∝ηs.But in any way,the present results are precise enough for our purpose.We note that these connecting parameters can be calculated in a semi-analytical scheme[37].A similar method is discussed in section 5,in which the connecting parameters are traced by choosing the proper root of a polynomial with increasing order.The biggest problem of such semi-analytical schemes is to find the right root of a high-order polynomial,which is computationally expensive,meanwhile the improvement on the precision of ksis very limited in comparison with the results from the extrapolation method.
4.Two-point Padé approximants for the vortex solution
Analytically,we may try to mimic the solution to equation(4)in terms of Taylor expansion series from both points η=0 and η=∞simultaneously.This is the basic idea of two-point Padé approximants.Without loss of generality,we may define g(η)by taking a shift 1/2 in f(η),g(η)=f(η)-1/2,and then expand g(η) at η=0 and η=∞in the form
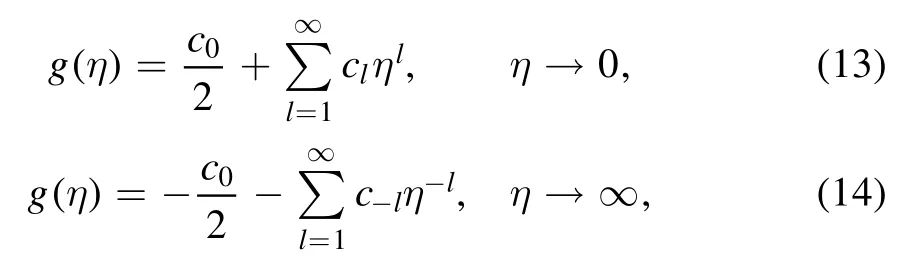
where c0=-1 and other coefficients c-i,…,cican be derived from equation (4).For η=0,by inserting equation (13) into equation (4),we find cl=0 for 0<l<s and a recursive relation for clfor l≥s,

Table 1.The numerical values of RN and k1ext extrapolated from RN.
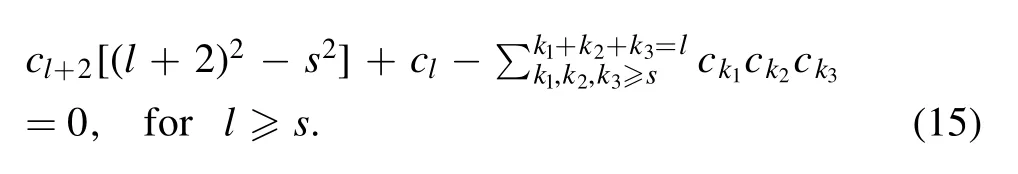
The last term on the left-hand-side of equation(15)comes from the nonlinearity of equation (4).Without this term,the coefficients are just those of Bessel’s functions of the first kind.For the complete form,we can read out that only the coefficients with even/odd indices can be nonzero for the even/odd s,and their values are solely determined by the first nonzero one,which is cs=ks.Take s=1 as an example,we have
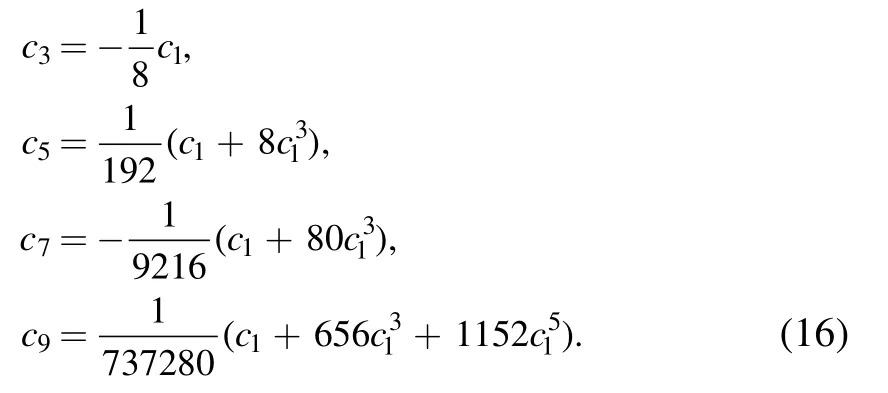
For η=∞,we insert equation (14) into (4) and obtain c-1=0 and a recursive relation for c-lwith l≥2,
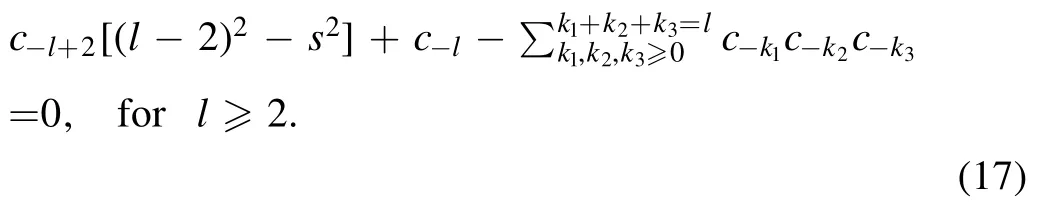
It can be read out that all coefficients with odd indices are vanishing,the values of coefficients with even indices are solely determined by s.For the case s=1,we have
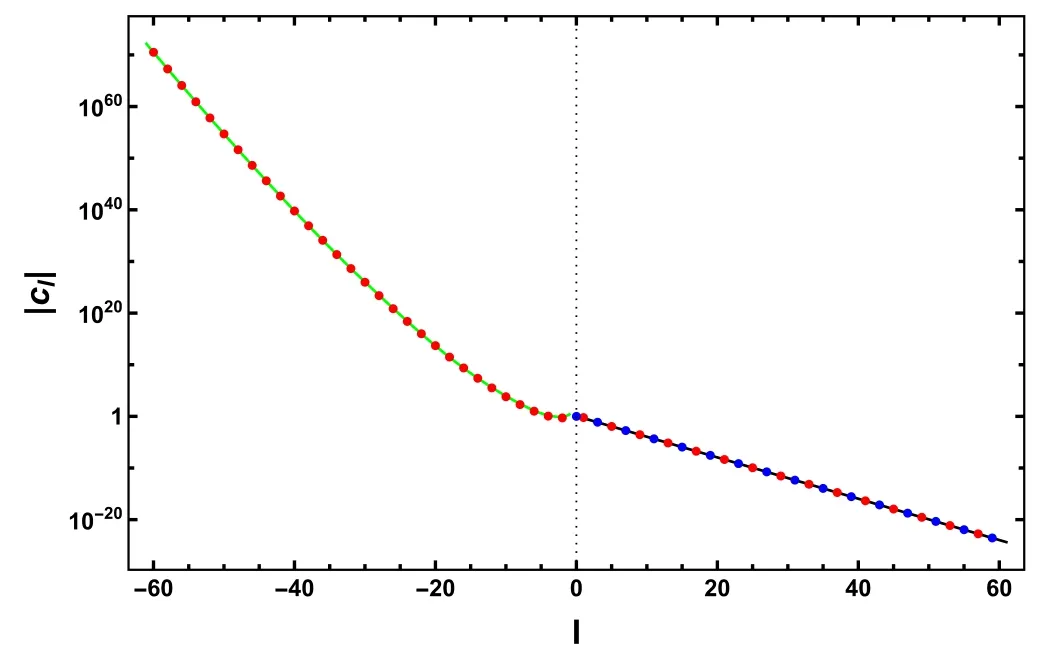
Figure 3.The coefficients cl for s=1.The absolute values of cl are shown in a logarithmic scale,the sign of cl is indicated by the color of the point: red/blue stands for the positive/negative value.The green solid line stands for 1.92×2l/2Γ[-l-1/2].The black solid line stands for 1.125×2.512 1034-l.
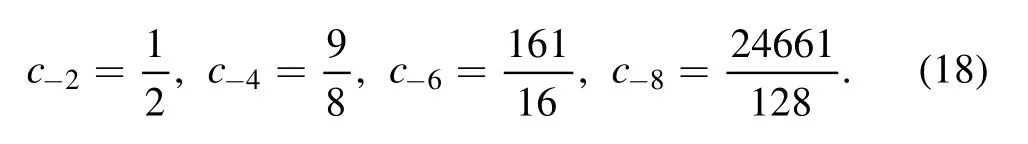
In figure 3,we show the values of coefficients clfor s=1,where c1takes the value ofk1ext.The absolute values of nonzero coefficients are shown in a logarithmic scale,the sign of each coefficient is indicated by the color of the point:red/blue stands for the positive/negative value.The magnitude of nonzero clwith l≤0 is fitted by 1.92×2l/2Γ[-l-1/2]as the green solid line.The absolute values of nonzero clwith l >0 is fitted by 1.125×2.512 1034-las the black solid line.So that we can read out the convergence radius for the series in equation (13) is about 2.5,while the convergence radius for equation(14)is zero if we take 1/η as the expansion variable.It seems that polynomials of Taylor expansion cannot approximate the solution to equation (4).We have to seek a new type of function to incorporate the boundary conditions from both sides and describe the numerical solution in the whole range 0<η<+∞.
The two-point Padé approximants in terms of rational functions have the form
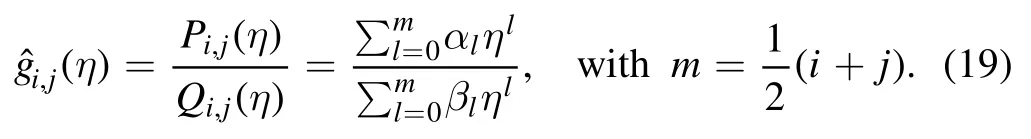
In this form,Pi,j(η) and Qi,j(η) are polynomials with the truncation order m,and αland βlare the coefficients determined by requiring that the expansion of(η)at η→0+and 1/η→0+agrees with equations (13) and (14) up to and including ci-1ηi-1and c-jη-jrespectively.So the residues of the approximants are of the order i and j+1 at the boundaries,i.e.
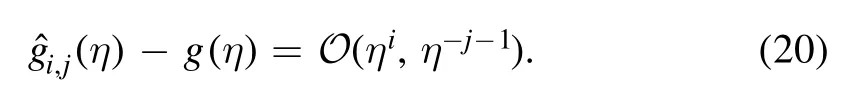
With clin equations (13,14),the polynomials in the numerator and denominator in equation (19) can be constructed in a determinant representation [36],
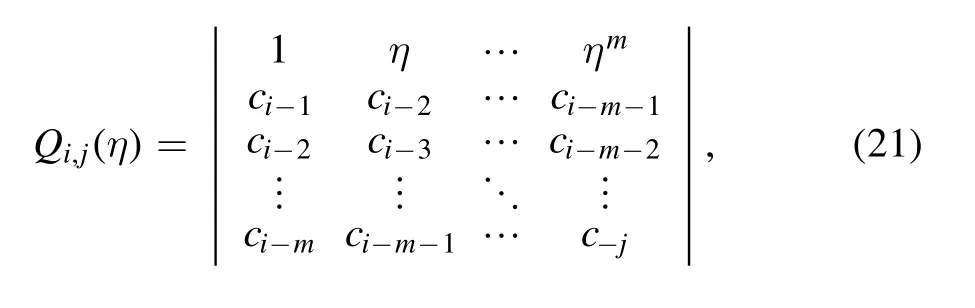
and Pi,j(η) is obtained from Qi,j(η) by replacing the first row with the vector

where Sk(η) and Tk(η) are defined as
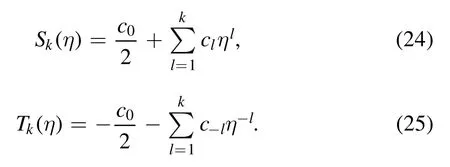
Note that equations (24) and (25) are just the series of equations (13) and (14) up to k respectively.
In such a way,the two-point Padé approximants for the solution to the ODE (4) can be easily constructed.The truncation index (i,j) sets the size and structure of Pi,jand Qi,j,while the numerical value of each matrix element can be determined by the recursive relations in equations (15) and(17) with the connecting parameter cs=ks.But in practice,the expected precision in comparison with the numerical solution is not guaranteed by the constructed function (19),although kscan be determined with extraordinary precision.The quality of the result depends on the choice of(i,j),so we have to check whether the required accuracy can be achieved for particular values of i and j.We regard the high precision numerical solution discussed in the previous section as an‘exact’solution,from which the accuracy of the approximants can be estimated.For the primary vortex with s=1,an economic approximate function is given by setting i=9 and j=3,which is the best choice for m=(i+j)/2≤6.The constructed function is parametrized with 12 coefficients in the form

The Taylor expansion of this fractional polynomial can reproduce c1,…,c8for η→0 and c-1,…,c-3for→0.max[∣(η)-f(η)∣],is about 1.2×10-3,as shown in the left The accuracy of the function with i=9 and j=3,defined by panel of figure 4.It is much better than one general-purpose interpolation routine with limited input data points.The accuracy can be significantly improved for larger m,as shown in the middle panel of figure 4,the accuracy is about 1.5×10-8for the function with i=26 and j=10.The coefficients in this function are listed in appendix B.This approximate function with 36 parameters is good enough for the precise simulation of vortices within GPE.
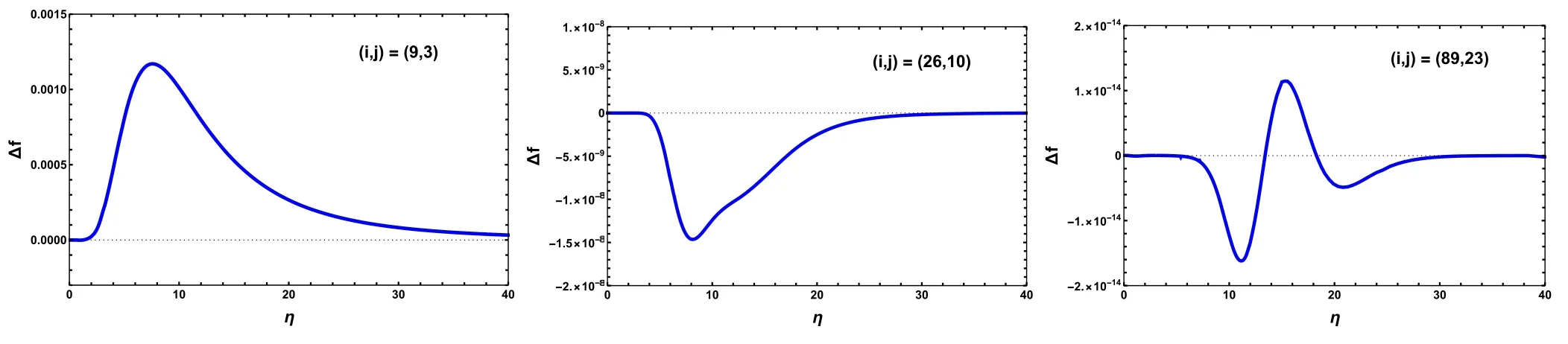
Figure 4.The difference between the approximate functions and the ‘exact’ solution for three typical truncation indices.
In the same way,the two-point Padé approximants for the profile functions of vortices with larger winding numbers can be achieved.The coefficients of the fractional polynomials for s=2,3 are given in appendix B.In both cases,the accuracy is better than 10-6in the whole range of η.It is interesting to see that the approximants with even s contain only even terms in Pi,jand Qi,jbecause the coefficients clwith odd l are all vanishing in equations (13) and (14).
Before we work on even higher order functions,we must keep in mind that the coefficients will all change if we choose different i and j.The reason is that the polynomials in the numerator or denominator result from matrix determinants,any change to the matrix will give very different polynomials.So we cannot expect the coefficients of polynomials will be determined order by order as in a perturbation theory.
To explore the limit of this method,we try to calculate Pi,j(η) and Qi,j(η) for large i and j.The problem is that the matrices of Pi,j(η) and Qi,j(η) involve coefficients clthat differ dramatically in magnitudes as shown in figure 3,it is a numerical challenge to keep the precision in calculating the determinant of such matrices of large dimension.We found Mathematica can handle these matrices with i≤100 and m≤60.The best approximate function that can be accessible corresponds to the matrix for i=89 and j=23,the accuracy is of the order 10-14,as shown in the right panel of figure 4.The structure and coefficients of the rational functions may indicate some hints for the exact solution to the nonlinear ODE.In appendix A,we give an example of how the Padé approximants help obtain an exact solution to a nonlinear ODE.But for equation(4),we fail to find any hint for an exact solution except approximate functions at very high precision.
5.Error estimation and challenge
The precision of Padé approximants cannot be improved by simply increasing the truncation order.The asymptotic errors for both boundaries can be estimated as

with Dr,tbeing the determinant of the coefficient matrix
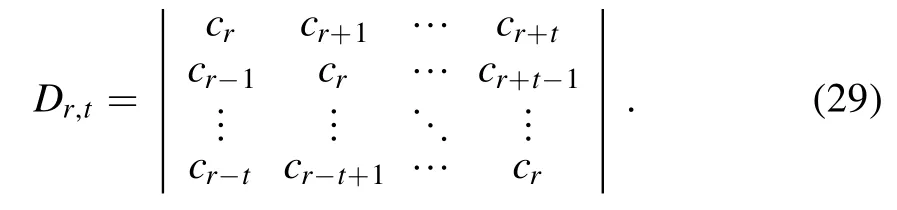
The error for small η is controlled by the ratio|Di-m,m/Di-m-1,m-1|.To have an intuitive idea about the ratio,we estimate it as a function of m for the case i=j=m.As shown in the left panel of figure 5,the ratio can be approximated as 102×5.5-m.This feature reveals that the convergence radius ofhas been extended from 2.5 to 5.5 by Padé approximants for small η.For large η,the dependence of |D-1,m/D0,m-1| on m is shown in the right panel of figure 5 and can be described by 10-10×18m.This means that the error is under control for η >18,or the convergence radius for 1/η is extended from 0 to 1/18.Although the change of the convergence radius is small,the coverage range of the approximants is expanded significantly.Actually,this is a remarkable progress of Padé approximants which aim to reproduce a complicated function from both boundaries simultaneously.Inside the gap between two convergence regions,the rational function connects both regions smoothly,which should reproduce the target function with a similar or slightly worse precision if the target function does not contain a singularity in the gap.The error can be further reduced by fine-tuning of i and j if the target function is known with higher precision.As we have already shown in figure 4,the vortex profile function can be reproduced with high accuracy,and the behaviors of errors can be well understood as discussed above.
In the description of Padé approximants for vortex profiles,we find that Pi,j,Qi,jand Dr,tare sensitive to the connecting parameter ks.Since the corresponding matrices have a similar structure,we take Dr,tas an example to discuss its dependence on ks.For simplicity,we look at D0,mand k1.From equation(29),D0,mcan be expressed as a polynomial of c1and the order increases fast with the dimension of the matrix.We find that D0,mhas some real roots,denoted as c1i,which are very close to k1.The distance between each c1iand k1is shown in figure 6,where the magnitude is plotted in logarithm scale and the sign is marked by color.A bunch of roots near k1indicate that D0,mvaries dramatically when c1approaches k1.So it can be understood that a small deviation from k1will lead to an uncontrollable variation of Dr,twhen the dimension of the matrix becomes large.Similar behavior is also observed in Pi,jand Qi,jas functions of c1.So the accuracy of the Padé approximants for large m strongly depends on the precision of k1.As shown in figure 7,for the best result that we find (the right panel of figure 4),a very small change in the value of k1leads to a significant increase in the error of the approximants.So the precision of k1is crucial for that of Padé approximants for large m.
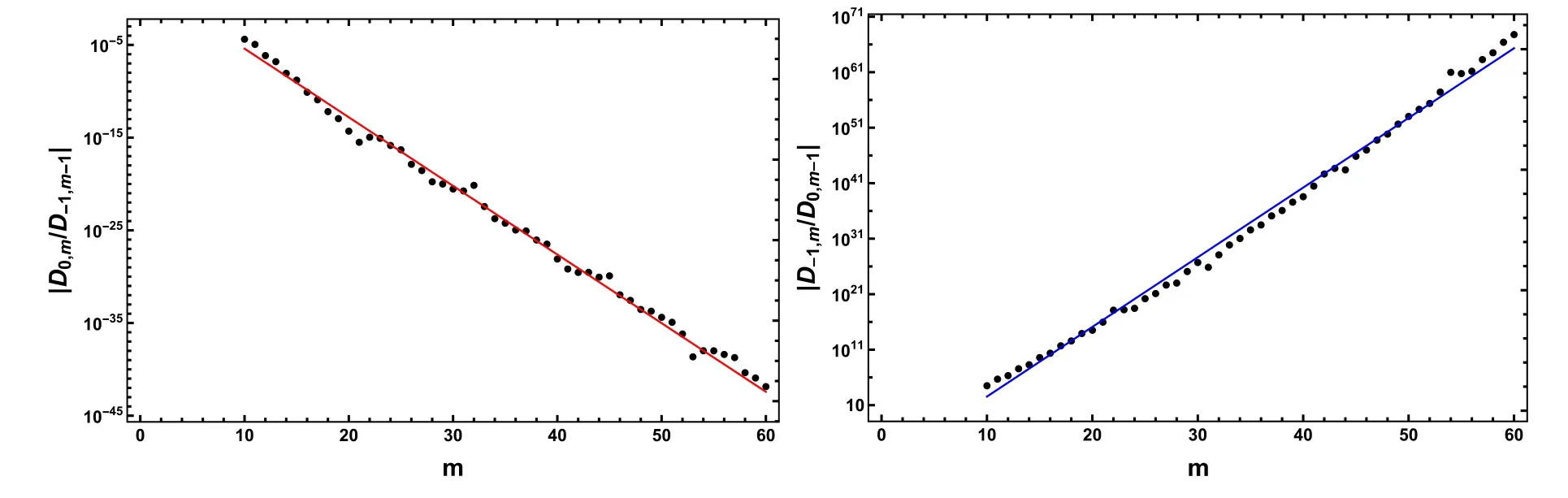
Figure 5.Left:the ratio|D0,m/D-1,m-1|(points)varies with m,the red line shows the function 102×5.5-m.Right:the ratio|D-1,m/D0,m-1|(points) varies with m,the blue line shows the function 10-10×18m.

Figure 6.The relative distance between k1 and the roots of D0,m for different m.The magnitude is shown in logarithm scale,while the sign is indicated by color: red points stand for c1i > k1,blue points stand for ci k1< 1.The bottom line indicates the chain of the closest roots,which is technically traceable without knowing k1 at first.
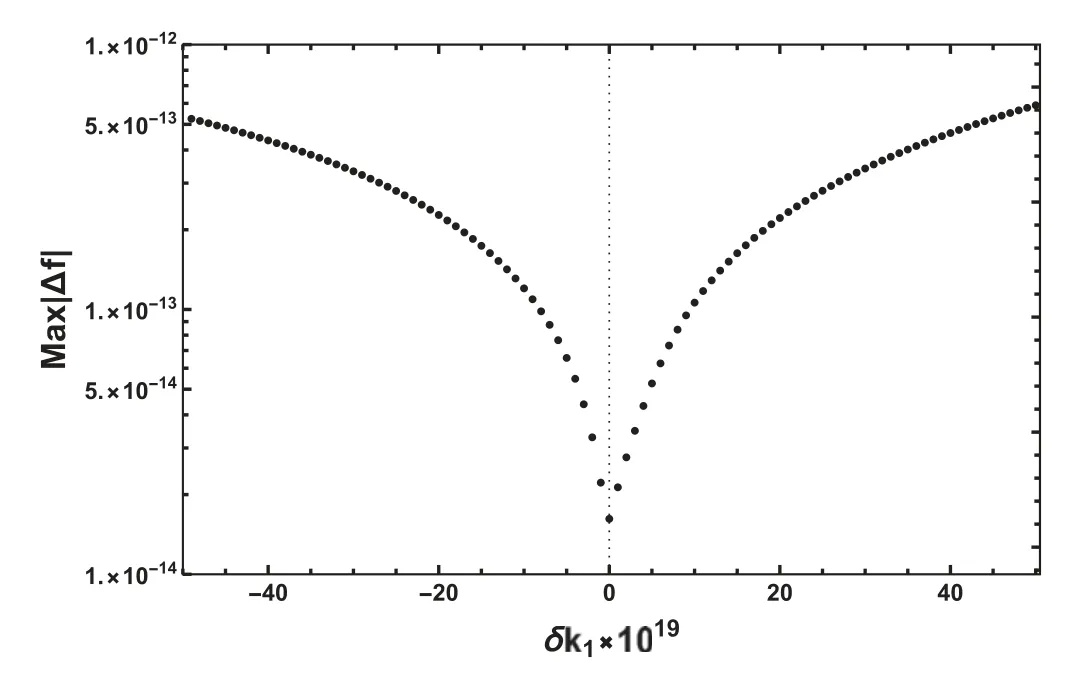
Figure 7.The maximum deviation of the approximants from the‘exact’ numerical solution as a function of the variation of k1.
The minimal distance in figure 6 can be extremely small for large m,it seems that this feature can be employed to find the asymptotic value of k1from c1iwith a carefully chosen initial value and iteration of increasing m.Technically,we can set the only possible root of D0,4as the initial value,and replace it with one root of D0,5which is real and closest to the original one.Repeat this procedure,a chain of the closest root can be found,approaching the true value of k1.As shown in figure 6,the bottom line is traceable without knowing k1at first.This idea is workable for m<80,with the precision at the level of 10-12.But for even larger m,it is difficult to find the right root of a highorder polynomial,because the density of roots near k1increases while the minimal distance between them decreases exponentially,which raises the risk of finding wrong roots.This is the reason why we do not seek the value of k1from roots of Dr,tbut import the extrapolated value from a series of numerical solutions with a reliable precision.At the present stage,with Mathematica running on a laptop,we can confirm the value of k1with 17 significant digits,which helps us to promote the precision of the two-point Padé approximants to 10-14.The method may help us to search for the exact solution of the vortex profile.
6.Summary and conclusion
Understanding the vortex dynamics is important for the study of superfluids and many other physical systems.Due to the nonlinear nature of the vortex dynamics,the evolution of the vortex can only be studied in a perturbative way,which requires a high precision solution to the stationary wave function of the vortex.The nonlinear ODE for the vortex profile function can be solved numerically with high precision.
For practical applications,we have constructed semianalytical solutions to this problem with two-point Padé approximants.These solutions are presented with simple rational functions,which have a high accuracy and are ready for use in the precise simulation of the vortex dynamics.The coefficients of rational functions strongly depend on the value of the connecting parameter which can be obtained in a high precision from an extrapolation of the numerical solution or a systematic root-finding in a series of polynomials.
The accuracy of the approximate solutions can be improved significantly with a reasonable extension in the order of rational functions.With a systematic scan of the truncation orders,the best accuracy is found to be at the order of 10-14.The errors of the approximate functions and the limitation of two-point Padé approximants are discussed,which can extend our understanding on the nonlinearity of the vortex dynamics.This investigation may provide the clue for an exact solution to the vortex profile function.
The methods and algorithms developed in this work for high precision solutions to the vortex equation can be applied to other nonlinear systems,such as the Schrödinger–Poisson problem[38,39],the shape and properties of Bose stars formed by dark matter through the universal gravitational interaction and so on.
Acknowledgments
J D is supported by the Natural Science Foundation of Shandong Province under Grant No.ZR2020MA099.Q W is supported in part by the National Natural Science Foundation of China (NSFC) under Grants No.12135011,11890713 (a subgrant of 11890710),and by the Strategic Priority Research Program of the Chinese Academy of Sciences (CAS) under Grant No.XDB34030102.
Appendix A.An example for exact solution with twopoint Pade approximants
We consider the nonlinear ODE
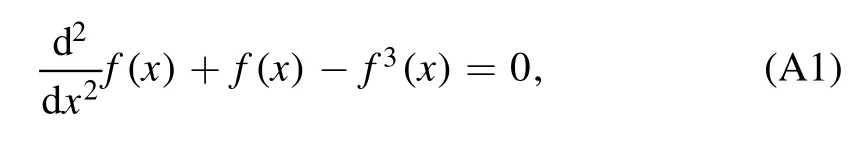
with the boundary conditions f(0)=0 and f(∞)=1.At the zero point,we may insert the formal solution

into the ODE.It is easy to check that all even terms are vanishing,i.e.c2k=0 for k=0,1,….The odd terms satisfy the recurrence relation
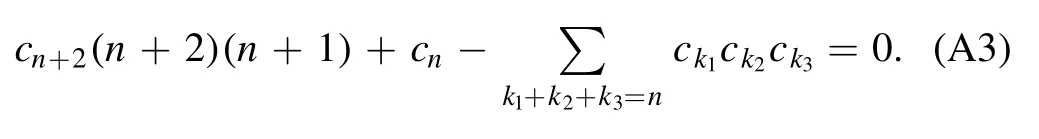
The only unsettled parameter is c1,by which other coefficients can be expressed,for example,we have the following expressions for c3,…,c9in terms of c1

We may represent the solution in the form of Padé approximants
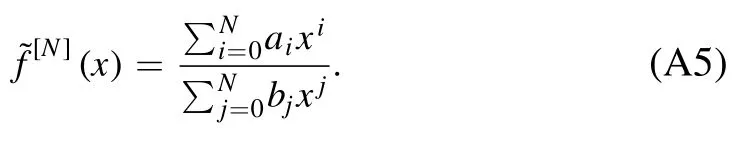
Because the solution is determined by the ratio,it is natural to demand b0=1.Because c0=0,we can set a0=0.Other coefficients should satisfy
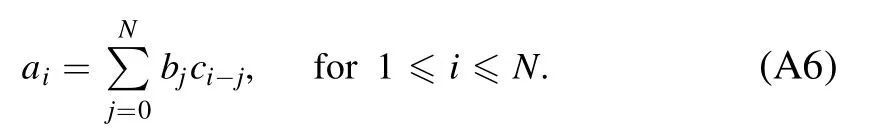
For the boundary condition at x→∞,we can change the variable to z=1/x,so that equation (A1) can be rewritten as
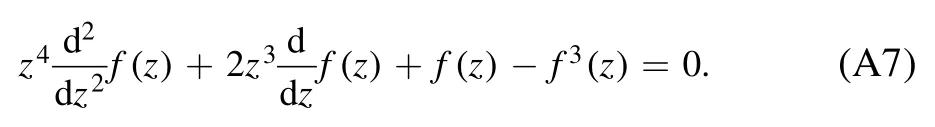
Then we can take the formal solution in the form

It is easy to obtain d0=1 and di=0 for i >0.So there is another constraint for coefficients

Combining equations(A6)and(A9),we obtain a set of linear equations for (a1,…,aN) or (b1,…,bN).We may write the equations into a matrix form.As an example,the equations for N=5 read
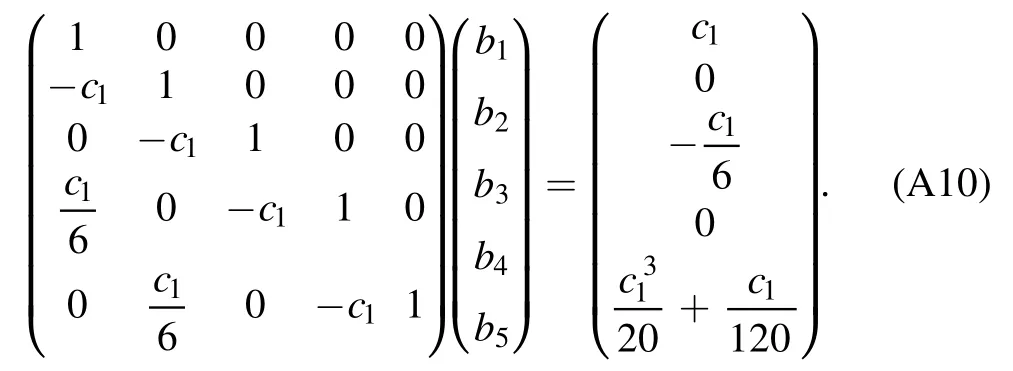
Because the matrix is already in a triangle form,the solution can be easily obtained

To determine the value of c1,we may demand one more constraint on the solution by taking aN+1=bN+1=0,which can be written as

It gives an algebra equation for c1.As an example,for N=5,the equation reads

The meaningful root to the above equation is≈0.687 481.In this way,we can get a series of c1values 0.69976,0.704 416,0.706143,0.706768,0.706989 for N=6,7,8,9,10 respectively.We may check that the approximate value of c1becomes closer tofor large N.If we setwe find the solution in equation (A11) can be simplified toSo the solution can be put into the form
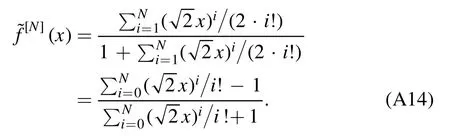
It happens to givef(x)=if we send N to ∞.
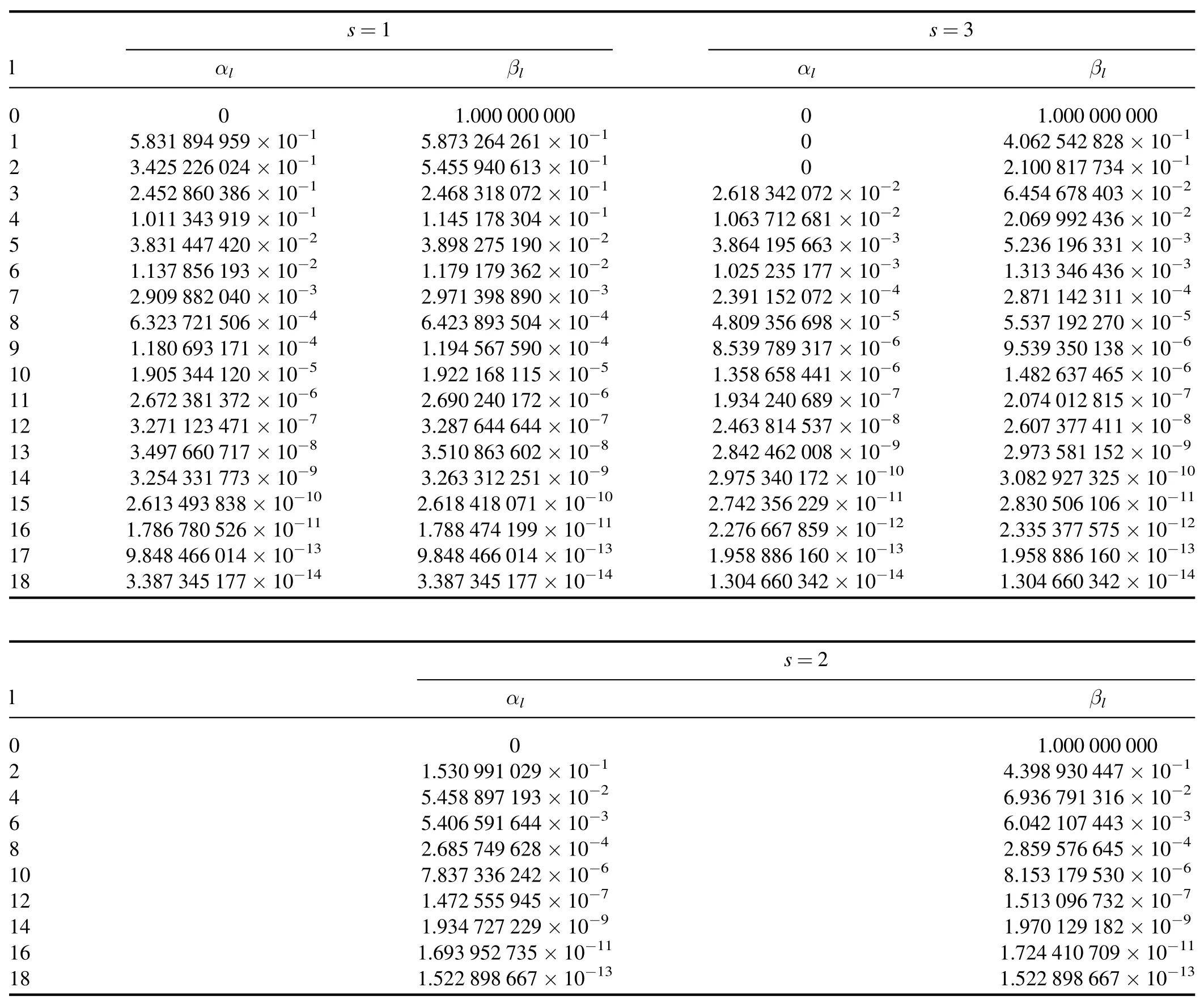
Appendix B.Coefficients in approximate functions for vortex profiles
In this appendix we list the coefficients in approximate functions in (19) with which one can reproduce the vortex profiles in high accuracy.
?
ORCID iDs
杂志排行
Communications in Theoretical Physics的其它文章
- Preface
- Phase behaviors of ionic liquids attributed to the dual ionic and organic nature
- Chaotic shadows of black holes: a short review
- QCD at finite temperature and density within the fRG approach: an overview
- The Gamow shell model with realistic interactions: a theoretical framework for ab initio nuclear structure at drip-lines
- Effects of the tensor force on low-energy heavy-ion fusion reactions: a mini review
