金属冶炼过程中材料成本用量数学建模计算方法
2022-10-21夏冰心
夏冰心
(甘肃工业职业技术学院,甘肃 天水 741025)
高精度金属冶炼是保证金属行业生产与作业效率的关键环节,可以认为金属冶炼的效果不仅会影响到产出成品的质量,也会对生产单位的经济收益、生态效益造成直接的干扰。在对金属冶炼全过程进行分析时发现,此项工艺中涉及多个较为复杂的环节,无论任何一个环节,都要做好对生产过程材料成本用量的计算,掌握不同材料在生产过程中的使用量与使用成本,以此种方式,将生产作业效率控制在一个相对较高的水平。目前,针对此方面的研究,我国已开展了多次研究,并提出了多种用于计算金属冶炼材料成本用量的技术[1]。但传统的方法大多需要在计算中辅助大量数据作为支撑,包括金属冶炼过程中的工艺参数、产量数据等,然而在实际生产中,大量的数据以模糊数据方式存在,获取精准的计算参数不仅需要大量时间,也需要投入集中的人力,整体耗时较长十分不利于金属冶炼加工生产方的持续化作业。为了进一步提高材料成本用量的精度,满足企业高效率生产作业需求,本文将设计一种针对金属冶炼过程中材料成本用量的数学建模计算方法,使用数学模型,开展此项作业,保证对金属冶炼生产成果质量的提升,实现对产业经济效益与企业可持续发展能力的全面保障与优化。
1 金属冶炼过程中材料成本用量数学建模计算方法
1.1 金属冶炼过程中不同作业工况识别
为实现在金属冶炼过程中,对材料成本用量的精准计算,需要在设计方法前,进行金属冶炼不同工况的识别。结合不同作业工况的需求,掌握不同生产作业阶段对投入材料成本的要求[2]。
通常情况下,金属冶炼生产作业过程中的各项工况参数需要由终端技术人员,根据其个人工作经验进行识别与判断,尽管此种方式可以基本满足生产需求,但识别与判断的结果极易受到个人主观影响出现盲目性问题。为了避免此种主观性偏差对生产单位产出成果的质量造成影响,可先假设金属冶炼过程中的工况共有N种,则N={n1,n2,n3,…,nm},建立针对N的多维度观测矩阵,对不同生产工况下的作业模式进行识别与判断[3]。其中多维度观测矩阵表达式如下:

公式(1)中:R表示为多维度观测矩阵表达式;r表示为矩阵子集;p表示为矩阵的列数。在上述构建的观测矩阵中,其中每一行都可以代表在一个相同作业工况下,金属冶炼生产的数据,每一列都可以代表在不同作业工况下,金属冶炼生产的观测值数据。识别在此过程中的行数与列数,掌握金属冶炼生产过程中材料成本用量的不同工况条件。
1.2 基于数学建模的多工况下材料成本用量数据聚类
完成对工况的识别后,考虑到不同工况下,材料成本用量是存在显著差异的,而仅依靠人工进行差异的计算与用量数据的统计,可能存在结果偏差。因此,引进聚类模型,对相同工况下的生产数据进行观测,计算有效观测距离,如下计算公式(2)所示。
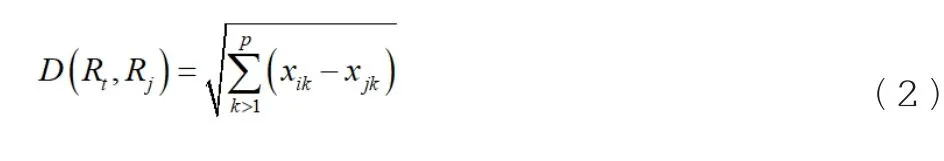
公式(2)中:D表示为相同工况下生产数据的有效观测距离;Rt表示为聚类有效时长;Rj表示为聚类过程中的有效迭代次数;x表示为聚类因子;i表示为因子数量;k表示为观测值类别。在对生产数据进行观测时,需要将距离最远点作为材料成本用量数据的聚类中心点,从中心点开始逐步向外进行迭代。按照此种方式可以计算得到k个有效聚类中心,将中心作为生产簇族值,进行生产数据簇族的多次生成,通过对簇族规模的比对与分析,实现多工况下材料成本用量差异的获取。
在此基础上,引进神经网络模型,对生产过程中的各项指标进行聚类,通过此种方式,掌握在相同工况条件下,材料成本用量的差异。
在此过程中,需要将神经网络模型划分成一个多节点的三层结构模型,将生产过程中的用量数值迭代次数、关键节点等数值,按照指标序列进行导入。将导入后的数值进行多元回归分析,实现在不同维度下对材料成本用量数据的聚类处理。可将此过程表示为下述计算公式。

公式(3)中:V表示为基于数学建模的多工况下材料成本用量数据聚类过程;Q表示为材料产业差异系数;P0表示为金属冶炼过程中材料实际混合用量;P1表示为金属冶炼过程中材料标准混合用量;γ表示为可控因素。按照上述步骤,完成对成本用量相关数值的聚类处理。
1.3 基于影响因素分析的材料成本用量精准计算
完成上述设计后,考虑到金属冶炼过程存在大量的不可控因素,这些因素会在不同程度上对材料成本用量造成影响。为了避免影响因素对材料成本用量数学建模计算结果造成影响,需要在输出计算结果前,根据影响因素对的发生概率与指数,进行用量值的补偿,以此种方式,确保计算结果具有高精度优势。将影响因素设定为B,可将B描述为{b1,b2,b3,…,bs},其中b表示为影响因素的分项指标,对B中的影响因素进行相关性分析,掌握不同因素之间的关联性与相互模式。在此过程中,提出一种零假设,即B中任意两个影响因素之间的相关性为0(即任意两个影响因素之间不存在关联),计算此种情况的发生概率。计算公式如下:

公式(4)中:G表示为零假设情况的发生概率;y表示为影响因素显著性条件;e表示为样本观测量;λ表示为两个影响因素之间的关联系数,取值在(0~1)之间,取值越接近于0,代表两者的关联性越低,取值越接近于1,代表两者的关联性越高。按照上述公式,掌握不同因素对材料成本用量的影响,计算在影响因素的干预下,金属冶炼过程实际所需的材料成本用量。以此种方式,实现对用量结果的精准计算,计算公式如下:

公式(5)中:U表示为材料成本用量精准计算结果;SSE表示为自变量与因变量的密切程度;μ表示为影响因素补偿值。按照上述公式,完成金属冶炼过程中材料成本用量数学建模计算。
2 对比实验
上文从三个方面,完成了金属冶炼过程中材料成本用量数学建模计算方法的设计,为了证明此次设计的计算方法在实际应用中可以为金属冶炼单位生产创造更高的经济效益。下述将通过对比实验的方式,对此次设计方法的可行性与实用价值进行检验。
实验前,在某工业园区进行走访,根据专家系统决策与多方商定,选定A企业作为此次实验的参与企业,在与企业进行交谈时发现,该企业正在进行一批高质量金属制品的生产,截至目前,生产单位已进行了为期3个月的金属原材料冶炼加工。但在对现有加工成果的质量检验中发现,金属冶炼加工成果的质量抽检合格率不足80.0%,为了解决此方面问题,生产单位已投入了大量资金用于生产设备与生产工艺的改造,但显而易见的是,现有投入并未在市场内取得显著的成果。为此,实验单位相关技术人员对该企业展开了调查,调查中发现,该企业出现金属冶炼质量问题的主要原因是,没有做好前期对材料成本用量的精准计算,导致批次生产的成果存在质量方面的不足。综合对金属冶炼单位的调研,明确了将该企业作为本文此次实验的参与单位。
实验前,先进行金属冶炼加工生产线的检查,根据该项目在建设过程中业主方的需求及其对产出成果的质量要求,进行金属冶炼过程中不同作业工况的识别。在此基础上,按照本文设计的内容,采用建立数学模型的方式,对不同工况下金属冶炼加工使用材料成本用量数据的聚类,掌握在生产时材料的基本需求。同时,分析并获取在生产加工线上可能对金属冶炼工艺造成影响或负面干扰的相关因素,将其作为参照,进行材料成本用量的补偿,实现基于数学建模计算的材料成本用量核算。明确本文设计方法的集成方式后,按照下述图1所示的流程,进行金属冶炼加工生产作业。
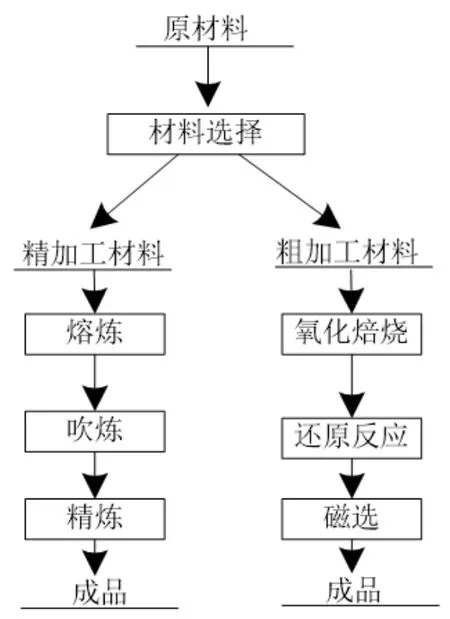
图1 金属冶炼加工生产作业工艺流程
上述图1所述的任何一个阶段都会存在不同程度与不同量的材料投放。因此,需要在每个生产阶段,都按照实际工序的需求,进行数学建模计算。按照计算的结果,精准投入冶炼生产材料用量。为避免本文方法在实际应用中的效果不佳,影响该企业的生产作业效率,设置一个本文方法在使用中的检验步骤,按照标准化生产作业流程,先生产一个批次的产品,对此批次产品进行五次随机质量抽检。将抽检合格率作为检验本文设计方法的评价指标,当抽检质量合格率在95.0%以上时,证明本文设计方法具有可行性,可以实现对金属冶炼过程中,不同工况下材料成本用量的精准计算。反之,当抽检质量合格率在95.0%以下时,证明本文设计方法在实际应用中仍存在漏洞与缺陷,需要采取必要的措施进行此设计方法的优化。按照上述方式,进行生产产品的质量抽检,记录五次抽检结果,如下表1所示。
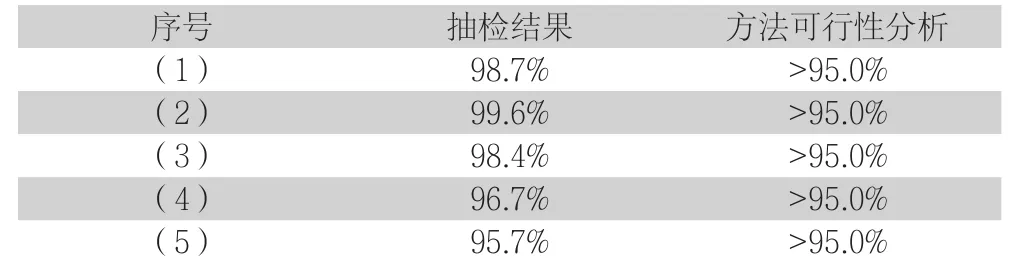
表1 金属冶炼加工生产作业五次抽检结果
从上述表1所示的实验结果可以看出,本文设计的金属冶炼过程中材料成本用量数学建模计算方法,在实际应用中具有一定可行性,可以实现对冶炼加工生产时投入材料用量的精准计算,保证产出的成果质量达标。
完成对本文设计方法的检验后,选择基于MATLAB GUI的建模计算方法作为传统方法。使用两种方法对相同批次的产品进行生产过程中的材料成本用量计算。将标准化生产中的实际需求用量与计算得到的材料成本用量进行比对,将两者生产后的成本用量精度作为对比指标。计算公式如下:

公式(6)中:F表示为金属冶炼过程中材料成本用量计算精度;x表示为金属冶炼过程中的影响因素;n表示为金属冶炼生产作业工况;f表示为冶炼中所使用材料的成本单价。按照上述计算公式,对生产过程中实际材料成本用量与计算材料成本用量进行比对,并按照上述计算公式,对结果精度进行计算,对比本文方法计算精度与传统方法计算精度,将对比结果绘制成曲线图,如下图2所示。
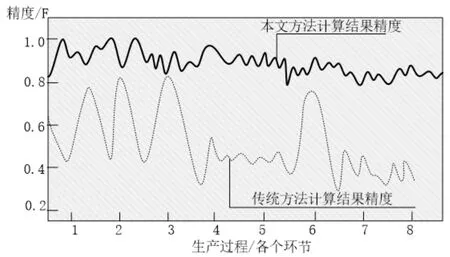
图2 金属冶炼过程中材料成本用量精度对比
从上述图2所示,使用本文方法进行金属冶炼过程中材料成本用量的计算,计算结果精度值基本可以控制在0.8~1.0范围内,使用传统方法进行金属冶炼过程中材料成本用量的计算,计算结果精度值基本可以控制在0.8~0.4范围内。通过对精度值的比对分析可知,本文设计的金属冶炼过程中材料成本用量数学建模计算方法,在实际应用中的计算结果精度更高,可以实现对材料成本用量的高精度计算。
3 结语
本文从金属冶炼过程中不同作业工况识别、多工况下材料成本用量数据聚类、基于影响因素分析的材料成本用量精准计算三个方面,开展了金属冶炼过程中材料成本用量数学建模计算方法的设计。并通过设计对比实验的方式,证明了本文设计的方法,在实际应用中的计算结果精度更高,具有代替传统方法在市场广泛推广使用的可行性。但在后续的研究中,还需要加大对此方法设计的投入,进一步完善计算方法的综合性能,以确保此方法在市场中发挥更高的使用效能,实现为我国金属冶炼行业的发展给予助力。
