基于稀疏表达重构误差模型的小区域滑坡易发性评价
2022-10-20孙晨昊郑逸榛李俊斌霍姝涵
孙晨昊, 郑逸榛, 李俊斌, 霍姝涵
(中国地质大学(武汉) 地球物理与空间信息学院,湖北 武汉 430074)
滑坡是地貌演变过程中的一种重要块体运动形式,是一种典型的重大自然地质灾害,给人类生产、生活构成严重的威胁[1]。同时,滑坡影响因子本身的随机性和不确定性以及滑坡发生物理过程的非线性,决定了准确预报滑坡发生时间的极度困难性[2]。
研究滑坡的方法之一是建立地区滑坡的易发性评价体系,通过构建滑坡空间预测模型,对潜在滑坡灾害进行定量分析,可较准确地预测特定区域内潜在滑坡发生的空间概率。目前,滑坡易发性预测过程中广泛使用的机器学习被认为具有比数理统计模型更好的非线性预测能力[3-4]。然而在小区域的滑坡易发性评价中,常用的全监督机器学习方法往往受到滑坡灾害点的数量不足与非滑坡灾害点的选取不准确的问题而影响到区域机器学习分类器的性能:滑坡灾害点数量不足容易导致模型训练出现“过拟合”现象,即模型在区域的泛化能力不足;非滑坡灾害点选取不当极易使模型分类器学到非典型特征,影响分类准确度,得到了诸多错误的分类结果。
近年来稀疏表示技术在信号处理、图像处理、目标识别、盲源分离等领域都有着突出的贡献,在计算机领域的人脸识别、目标检测、图像检索和恢复等方面取得巨大成功[5]。由于稀疏表示方法能有效解决高维特征空间的维数灾难和小样本问题,遥感领域的研究人员也将稀疏表示理论应用于遥感影像的恢复和重建、分类和目标识别等方面,并取得较好的效果[6]。受此启发,本文将“稀疏表达”思想引入滑坡易发性评价模型的建立,提出了一种基于稀疏表达重构误差的半监督滑坡易发性评价模型,用已有的滑坡灾害点来构建“滑坡字典”,无需选取非滑坡像元作为样本,充分利用已有的滑坡样本,较好地解决了小区域、少样本情况下的滑坡易发性评价问题,从而达到更为高效利用滑坡历史数据信息及提高滑坡易发性评价精度的目的。
1 评价模型
1.1 稀疏表达
稀疏表达的提出源于神经生物学,可追溯至1959年,人们发现主视皮层V1区神经元的感受也能对视觉感知信息产生一种“稀疏表示”[7],至此稀疏表示理论开始受到研究者的关注。1996年,Olshausen和Field[8]在《自然》杂志上发表开创性的文章,他们发现通过稀疏编码学习出来的字典具有人类视觉真实感受的特征。由此稀疏编码和稀疏表达理论开始被研究人员广泛关注。近年来稀疏学习理论逐渐趋于成熟,在信号处理、图像处理、人工智能等领域都有了广泛应用。
稀疏表达的核心是:用较少的基本样本的线性组合来表达大部分或者全部的原始样本。这些基本样本被称作原子,而过完备字典则是由个数超过特征维数的原子聚集而来。稀疏表达的根本意义在于:稀疏性,即低复杂度,这是物理世界的普遍特征。而稀疏性即低复杂度的表现,稀疏表达会更加体现系统的核心特质,也是系统结构的更优化的表示。稀疏性假设则是引入低复杂度对可能的模型进行加权筛选。
1.2 稀疏表达重构误差模型
本文基于上述稀疏表达原理,提出了稀疏表达重构误差模型,将区域内已有的部分滑坡像元组成“滑坡字典”,用“滑坡字典”重构出的像元与原有像元间的误差,即“重构误差”来刻画衡量区域内像元与滑坡特征模型的相似程度,以进行区域的滑坡易发性评价。具体步骤如下。
首先将研究区的所有像元作为数据集{x1,x2,x3…xn}。若用二维数组表示,则每一列为一个像元,每一行分别为高程、坡度、坡向等10项影响因素。紧接着用滑坡灾害点像元及其特征属性构建“滑坡字典”。找到合适的字典B,最后用尽可能少的字典原子来线性表示每一个像元,则像元的稀疏表达形式为:
xi=Bαi+e
(1)
图1和式(1)中:d=10,为像元特征数;k为字典的词汇量,也就是选取当作字典的滑坡数量;αi为某一像元的稀疏表达稀疏;e为对应的稀疏表达残差。不难证明,任一像元的稀疏表达系数αi不是唯一的,要找到最稀疏的那个组合以及稀疏表达系数αi,这就遇到了多项式复杂程度的非确定性问题(Non-deterministic Polynomial),难以求解。用数学符号表示,笔者希望找到一个αi,使其含有最多的0元素,即αi的0范数最小:

图1 稀疏表达原理图
(2)
s.t.xi=B·αi
(3)
这个命题可以等价转化为如下形式,找到一个最多只有η个非零元素的稀疏系数αi,使误差项e最小:
(4)
s.t.‖αi‖0≤η
(5)
这里可以采用正交匹配跟踪算法(Orthoganal Matching Pursuit)[9]求解某一像元对应滑坡像元字典的最稀疏系数。正交匹配跟踪算法的原理如图2所示。

图2 正交匹配跟踪算法原理图
最后,可以知道,选取了区域内的滑坡像元作为字典,那么对于区域内的某一像元而言,若其因子特征与滑坡像元的特征越相似,用“滑坡字典”来稀疏表达后的误差越小;若某一像元的因子特征与滑坡发育特征大相径庭,则用“滑坡字典”来稀疏表达后的误差是越大的。当然,这需要“滑坡字典”是一个过完备字典,即包含有较多的滑坡灾害点,记录区域内的普遍滑坡灾害点发育特征。于是就可以用稀疏表达后存在的误差,即“重构误差”来刻画衡量区域内像元与滑坡特征模型的相似程度,进行区域的滑坡易发性评价。
1.3 BP神经网络模型
神经网络属于动态非线性系统,它适用于处理背景知识不清楚,推理规则不明确,模糊、随机、复杂的信息识别问题[10],人工神经网络能为客观反映滑坡灾害地质体稳定性程度提供一条有效途径。
BP神经网络模型是1986年由Rumelhart和McClelland为首的科学家小组提出[11],是目前应用最广泛、最成功的神经网络模型之一。BP神经网络模型能学习和存贮大量的输入—输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用梯度下降法,通过反向传播来不断调整网络的权重和阈值,使网络的误差平方和最小。
BP神经网络模型拓扑结构包括输入层(input layer)、隐藏层(hide layer)和输出层(output layer)。输入层中各神经元负责接收来自外界的输入信息,并传递给中间层各神经元;中间层是内部信息处理层,负责信息变换,根据变换能力的需求,中间层可以设计为单隐层或者多隐层结构,其中隐藏层的节点个数经验公式为:
S=1+[m×(n+2)]0.5
(6)
式中:S为隐藏层的节点个数;m为输入节点数;n为输出节点数。最后一个隐藏层传递到输出层各神经元的信息,经进一步处理后,完成一次学习的正向传播处理过程,由输出层向外界输出信息处理结果。
1.4 信息量模型
信息量模型以信息论为基础,采用地质灾害发生过程中熵的减少来表征地质灾害事件产生的可能性,以影响地质灾害发生的因素为影响因子,通过计算各因子的信息量,进而将信息量单因素或加权叠加,建立易发性评价模型,对易发性作出评价[12]。对研究区多因子共同作用下的综合信息量的计算,可将各因子信息量进行单因素信息量叠加。如果用Ii表示影响因子xi的信息量,则有式(7):
(7)
实际计算时可用统计频率估计条件概率来估算信息量,则有式(8):
(8)
式中:S为研究区评价单元总面积;N为研究区含有地质灾害分布的地质灾害点总数;S0为研究区内含有影响因子x1x2…xn组合的单元总面积;N0为具有相同因子组合x1x2…xn的特定类别内的地质灾害点总数。上式可得到式(9):
(9)
式中:I为某评价单元信息量预测值;Ni为影响因子xi占有的评价单元中的地质灾害点总数;Si为含有影响因子xi的评价单元的面积。
2 万州区滑坡易发性评价
2.1 研究区概况
研究区为重庆市东北部万州区部分区域,位处三峡库区中段长江上游,面积约为404 km2。受亚热带季风影响,该区气候温暖湿润,降雨丰富,多年平均年降雨量为1 194.4 mm。万州区位于四川盆地东北部,地形以山地丘陵为主,东南部地势较高,长江两岸地势较低。境内的铁峰山、方斗山等属世界三大褶皱山系之一的川东平行岭谷,呈现出背斜成山、向斜成谷、山谷相间、彼此平行的褶皱地貌。区域内岩层主要为侏罗系和三叠系地层,岩性以砂岩、泥岩、页岩、灰岩为主,且人工堆积、冲积、残积、坡积物等土层分布也较为广泛。受构造作用影响,万州区褶皱发育密集,但并无大的断裂构造。区内地表水系发育,长江、数十条支流及小型溪沟构成了复杂的地表径流网络。正是由于上述复杂的工程地质条件,使得全区滑坡灾害十分严重,对人民生命和财产安全威胁巨大。

图3 万州区地质概况图
2.2 数据来源
本次采用的主要数据来源见表1。

表1 数据来源
2.3 指标体系与相关性分析
滑坡是内因和外因共同作用的结果,其发育受多种因素影响[13]。滑坡易发性评价影响因子的选择通常根据研究区的滑坡发育特征而定,同时需要分析各影响因子之间的相关性,以保持评价因子的相对独立性。本文提取了高程、坡度、坡向、地形湿度指数(TWI)、曲率、地层岩性、距构造线距离、距河流距离、距道路距离与土地利用类型共10个因子。
为确保各评价因子的相对独立性,保证评价模型的可靠性和精度,需对影响因子进行相关性分析。基于SPSS软件,采用Pearson(皮尔逊)相关系数分析影响因子的相关性,当系数值>0.5时,认为因子之间存在相关性,对评价结果准确性将产生影响[14]。计算结果如表2所示。
通过观察表2以及查阅相关系数界值表可得各指标皮尔逊相关系数值最大为0.469,绝对值均<0.5,说明各指标相对独立性较强,可用于滑坡易发性评价。

表2 因子相关系数表
采用高程、坡度、坡向、TWI、曲率、地层岩性、距构造线距离、距河流距离、距道路距离与土地利用类型共10个因子,绘制灾害点在各因子数据中的分布频率直方图(图4-图13),根据灾害点频率突变情况对各因子进行分级,各因子提取的图层与分级如表3所示。
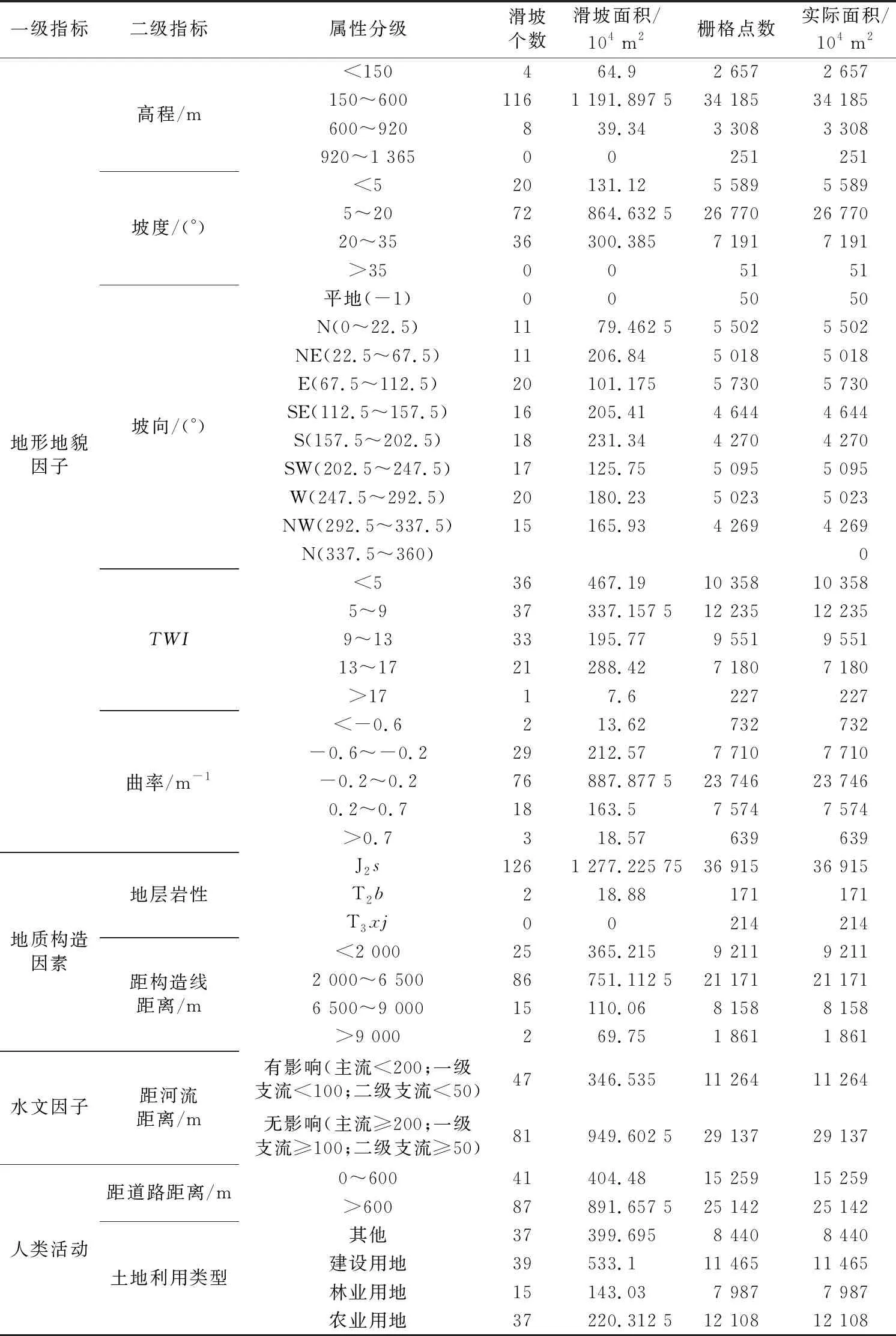
表3 各因子分级统计表
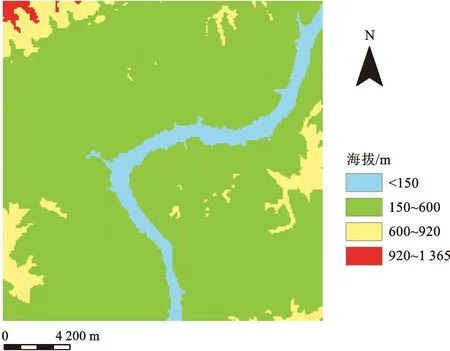
图4 高程因子分级图

图5 坡度因子分级图
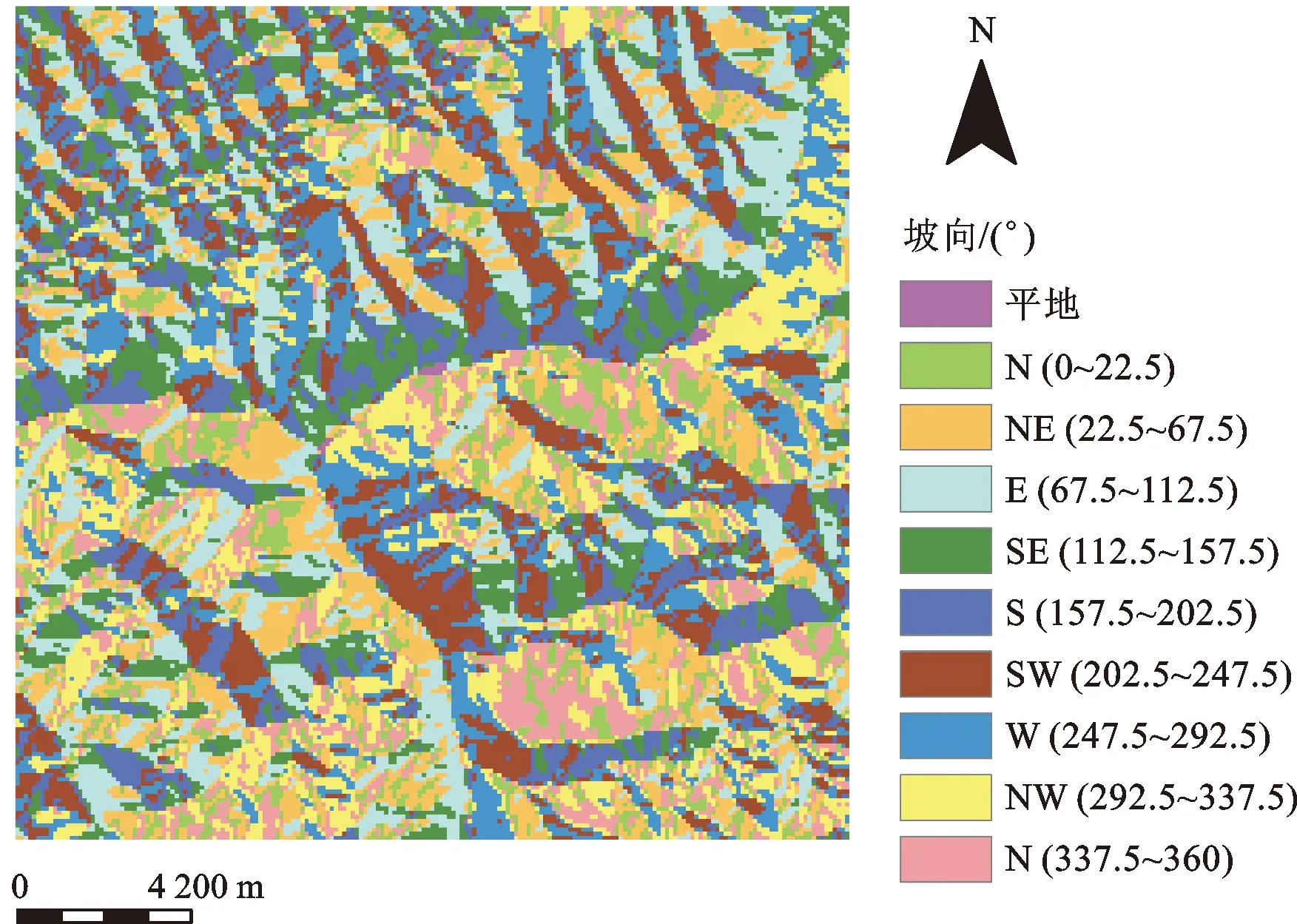
图6 坡向因子分级图

图7 地形湿度指数(TWI)分级图

图8 曲率因子分级图
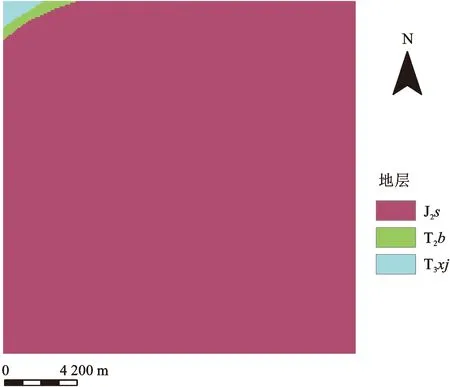
图9 地层岩性因子分类图

图10 距构造线距离分级图
图11 距河流距离因子分级图
图12 距道路距离因子分级图
图13 土地利用类型因子分类图
2.4 滑坡易发性评价
2.4.1稀疏表达重构误差模型
基于ArcGIS10.7与MATLAB平台,选取100 m×100 m栅格作为评价单元,研究区共划分40 401个栅格单元。收集和现场调查滑坡样本共计128个。具体评价流程如图14所示。

图14 评价流程图
(1) 字典构建。首先将滑坡灾害点数据及各评价因子数据导入。随机选取约70%的滑坡像元来构建“滑坡字典”。这里的70%数量是经过慎重考虑的:数量过多可能导致“滑坡字典”所记录的滑坡特征冗余,数量过少则难以构成过完备字典(即字典中的滑坡像元个数要远大于特征行数)。之后也尝试了将所有的滑坡像元纳入字典中。
(2) 字典与数据的规范化。将字典与数据进行规范化,这是进行稀疏系数求解的必要步骤。
(3) 稀疏系数求解与重构误差。对于图像中的每一个规范化后像元,运用正交匹配跟踪算法求解在“滑坡字典”D表示下的稀疏系数,同时计算其重构误差;计算出来的重构误差为规范化后像元每个特征的重构误差,之后需要求其F范数作为像元总的重构误差,将其作为像元的值。
(4) 还原图像与精度计算。以重构误差为评价指标,将所得的重构误差结果还原为199×199图像格式,并导入ArcGIS进行万州区域滑坡易发性制图,此处采用的分级方法为快速聚类分段法。之后绘制ROC曲线。将70%滑坡样本作为字典,利用快速聚类法[15]得到的聚类中心为0.104,0.168,0.225,0.29,0.568,由此得到的五个区划等级的分段点为0.136 3,0.196 8,0.262,0.433;得到的区划等级为:极高易发区[0~0.136 3),高易发区[0.136 3,0.196 8),中易发区[0.196 8,0.262),较低易发区[0.262,0.433),低易发区[0.433,0.788]。
2.4.2信息量模型
经过因子选择与分析,得到了影响滑坡灾害发育的10个因子及其图层,随后利用信息量模型计算各因子的信息量值,得到每个二级指标的状态指标的信息量。将每个因子的信息量图层进行叠加,得到最终的结果图层。最后采用快速聚类法[15]确定分级阈值,将结果图层的信息量值进行五级分类处理,通过聚类得到的分级阈值为:-2.279,-1.083 8,-0.033和1.087 8。由此得到的五个分级为:低易发区[-6.13,-2.279),较低易发区[-2.279,-1.083 8),中易发区[-1.083 8,-0.033),高易发区[-0.033,-1.087 8),极高易发区[-1.087 8,2.99]。
2.4.3BP神经网络模型
BP神经网络(back propagation neural network,BP)具有很强的非线性映射能力[16],可用于滑坡易发性评价。将各类滑坡影响因子作为网络输入层的变量,输出层则对应危险程度的具体数值表达[17]。故笔者基于MATLAB编程,使用了BP神经网络模型来进行万州区的滑坡易发性评价。
首先进行数据准备,将各因子图层从ArcGIS中导出,将导出的各因子图层和灾害点图层导入MATLAB中;然后对数据进行预处理,将二维因子图层转为一维的行向量,并且对因子归一化,这能够避免由于各因子取值范围的差异对BP神经网络性能造成的影响。随后进行标签准备,将滑坡样本与非滑坡样本进行样本标记;再选取训练样本,选取和已知滑坡栅格单元同等数量的非滑坡栅格单元,这里采用随机选取非滑坡像元,将相同数量的滑坡与非滑坡像元构成训练样本。然后进行BP神经网络训练,70%为训练集,15%为测试集,15%为验证集。根据经验公式,这里设置的隐藏层神经元个数为7个;最后依照分类结果进行图像还原,采用快速聚类法[15]将滑坡易发性结果图分为高易发区、较高易发区、中易发区、较低易发区与低易发区5类。
2.5 易发性评价结果及分析
滑坡易发性评价结果见图15-图18,易发性共分为5个等级,分别为低、较低、中、高、极高。从图中可以明显看出,历史滑坡点基本上都位于滑坡中等及以上易发区的范围,大多沿长江两岸分布,远离河流地区为滑坡的较低易发区和低易发区。
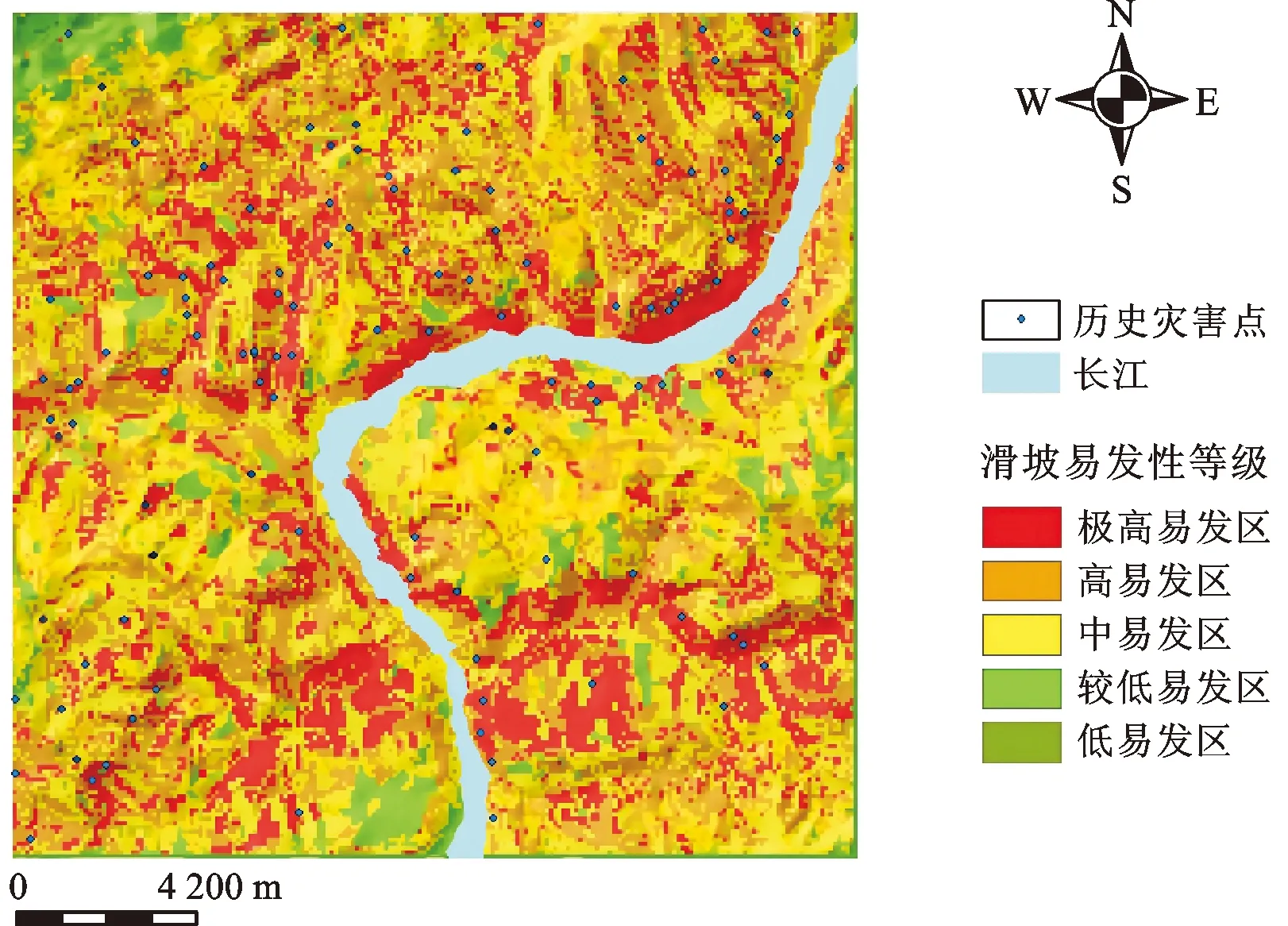
图15 万州区滑坡灾害易发性分级图(70%字典)

图16 万州区滑坡灾害易发性分级图(100%字典)

图17 信息量易发性分级图

图18 BP神经网络易发性分级图
2.5.1精度评价
根据易发性评价结果,统计滑坡各易发性等级所占面积、滑坡各易发性等级面积占研究区总面积的比例、滑坡数量、滑坡数量占总滑坡比例、滑坡面积和滑坡面积占研究区总面积的比例,详细数据见表4-表7。

表4 稀疏表达重构误差模型(70%字典)不同等级区划与滑坡分布统计表

表5 稀疏表达重构误差模型(100%字典)不同等级区划与滑坡分布统计表

表6 信息量模型不同等级区划与滑坡分布统计表

表7 BP神经网络模型不同等级区划与滑坡分布统计表
观察统计表格,从滑坡数量的分布来看,信息量模型和BP神经网络模型的结果在较低易发区与低易发区占比较少,滑坡大多分布在中易发区等级以上,说明了这两种模型有合理的预测效果,但是滑坡存在于极高易发区的比例均不是特别理想,相比之下,基于70%滑坡像元构建字典的稀疏表达重构误差模型在区域上取得了令人满意的结果。为了更好地比较三者的评价结果,通过计算两种模型易发性分区图的每个类别中存在滑坡的个数与每个类别总数的比值,即特定类别精度[18],其公式如下:
(10)
式中:Pj为特定类别精度,j=1,2…M(M为滑坡易发性分区类别的总数);Aj和Bj分别为第j类滑坡易发性分区中存在滑坡的斜坡单元个数和斜坡单元总数。三种模型的特定类别精度如图19所示。由图19可见,稀疏表达重构误差模型在高易发区的特定类别精度远远高于其他两种模型,由此说明,稀疏表达重构误差模型预测的滑坡易发性分区中高易发区等级以上包含了更多先前调查的滑坡。

图19 三种模型特定类别精度图
其中基于100%滑坡像元构建字典的稀疏表达重构误差模型所划分的极高易发区所占面积比为20.04%,略低于70%滑坡像元构建字典的稀疏表达重构误差模型所划分的极高易发区所占面积比(21.73%),但却包括了所有的滑坡灾害点。这个结果值得深思:将所有的滑坡灾害点用来构建字典,则所有滑坡灾害点所在像元的重构误差往往也取到极小值,故都落入极高易发区;换而言之,此时的“滑坡字典”记录了128个滑坡像元的所有模式,并且将区域上其他像元的特征模式与这128个滑坡像元特征比较,在一定程度上提高了字典的表达能力;然而这样做也存在一个比较大的缺陷,现实中存在如下情况:区域内存在偶然发生的滑坡灾害点,也就是说,128个滑坡灾害点并非全部在极高易发区,部分灾害点是偶然发生的,所记录的特征也不具备识别滑坡的可靠性,而是一种“噪声”,故将全部的滑坡像元充当字典是不妥的。
选用受试者工作特征(receiver operating characteristic,ROC)曲线线下面积(area under curve,AUC)、总体精度(overall accuracy,OA)和Kappa系数对三种模型进行评价。对曲线来说,曲线由图幅面积百分比和滑坡面积百分比确定,线下面积越大,越接近1,说明滑坡预测精度越高[19];而对OA与Kappa系数来说,指标值越大,模型精度越高。
如图20所示,稀疏表达重构误差模型、信息量模型及BP神经网络模型三种模型的线下面积(AUC)分别为0.834 3、0.655 2和0.680 3,三种模型中仅有稀疏表达重构误差模型AUC值>0.8,表明预测精度较高,较其他两种模型性能有明显的提升。除此以外,选用所有历史滑坡像元与随机选取的等量非滑坡像元进行精度评价,模型评价结果中极高易发区像元被认为是滑坡像元,其余像元则被认为是非滑坡像元,求得三种模型的混淆矩阵、OA及Kappa系数(表8)。由表8可以得知,稀疏表达重构误差模型的OA和Kappa系数均优于信息量模型和BP神经网络模型,表明稀疏表达重构误差模型在小范围的滑坡易发性评价方面有着良好的表现。上述结果说明稀疏表达重构误差模型是有效的,对小区域滑坡预测精度的提高具有一定帮助。

图20 模型ROC曲线图

表8 模型精度评价表
2.5.2模型稳定性分析
本文为了检验稀疏表达重构误差模型的稳定性,选取相同样本,在保持所有参数设置相同的条件下连续进行5次实验,得到OA、Kappa系数和AUC三个指标的稳定性分析结果(表9)。由表9可知,本文构建的稀疏表达重构误差模型在滑坡易发性评价中平均OA为78.86%,平均Kappa系数为0.577,平均AUC为0.828,稳定性较好。

表9 模型稳定性分析表
3 结论
滑坡灾害易发性研究在滑坡灾害风险管理与城市规划等方面具有非常重要的现实意义。本文结合万州地区已有的滑坡地质灾害点数据,基于GIS对其滑坡地质灾害的影响因子进行了分析评价。选取高程、坡度、坡向、曲率、地形湿度指数(TWI)、距构造线距离、距道路距离、地层岩性、距河流距离以及土地利用类型10项因子参与滑坡易发性模型建立。
本文将“稀疏表达”的思想引入滑坡易发性评价,避免了非滑坡像元的选择;小范围随机选取70%已有滑坡灾害点构建“滑坡字典”,通过重构误差来衡量某一像元与滑坡特征模式的相似程度,最后采用了快速聚类法进行易发性程度分段。除此之外,为了对比突出该模型的合理性,又使用了常用的信息量模型以及经典的机器学习模型——BP神经网络,从统计分析、制图结果、ROC曲线和模型稳定性等多角度评价结果表明,稀疏表达重构误差模型(70%字典)是一种更行之有效的方法。AUC值高达0.834 3,远优于信息量模型的0.655 2以及BP神经网络模型的0.680 3,除此外OA和Kappa系数也均优于信息量模型和BP神经网络模型,分别为78.1%和0.562,并且模型稳定性较好,制图结果与实际更符合。
可以说,将“稀疏表达”思想引入滑坡易发性评价模型的建立,是一次大胆且创新的尝试,取得良好结果的同时也值得进一步挖掘其背后更深层次的原理本质。未来的工作将围绕排除字典内偶然滑坡像元,选取更具代表性的“滑坡字典”原子以及找到一个最优的“滑坡字典”词汇量,而不是范式地选取70%滑坡像元。
