基于多项式法的地表移动变形计算模型修正

2022-10-20秦洪岩题正义

华中师范大学学报（自然科学版） 2022年5期

张峰，秦洪岩，题正义

(1.山西工程技术学院采矿工程系，山西阳泉 045000；2.辽宁工程技术大学矿业学院，辽宁阜新 123000； 3.华北科技学院安全工程学院，北京 101601)

煤层开采后，采场上覆岩层结构经历了从移动变形到变形破坏的过程，岩层的变形破坏自下而上波及至地表，使得地表的地形地貌出现不同程度变形破坏，影响矿区自然生态结构和构筑物的安全.由于不同区域煤层上覆岩层结构不同、岩石的性质千差万别，精确预计煤层开采后上覆岩层结构和地表的移动变形过程一直是困扰学者研究地表构筑物下煤层安全开采评价的主要难题，多数学者专家对此进行了一系列的研究.李世保[1]结合word和CAD研发了地表移动变形数据处理与预计一体化系统，克服了传统方法只能查看，不能定量分析的不足.李青峰[2]对比分析数值模拟和概率积分法预计地表移动变形值的结果，认为数值模拟得到的结果较为准确.周婷婷[3]分析了地质采矿条件对地表移动参数的影响机理，得到了各参数与地质采矿条件之间的对应关系，对该矿区地表移动变形预计提供了较高的实用价值.贾林刚[4]利用相似模拟方法研究了软岩煤层组的采动力学演化特性、顶板破断发展轨迹和地表移动变形规律，揭示了围岩移动变形过程中的影响因素.韩永斌[5]利用现场监测方法研究了厚煤层采动后地表移动变形大小和变形破坏规律，有效控制地表出现非连续变形.季鲲鹏[6-8]通过数值模拟和相似材料模拟研究了煤层开采后地表移动变形与预计参数之间的关系，对预计公式进行修正.综上，大多数学者对于概率积分法预计地表移动变形存在误差较大的问题具有共鸣之处，常采用数值模拟和参数修正等方法，没有从不同地质条件和计算公式推算过程上去开展相关研究工作，为此，依据地表下沉值与其它移动变形值之间的计算原理关系，结合煤层开采后地表移动变形计算结果和实测结果，本文提出了利用多项式法对计算模型进行修正的方法，构建基于概率积分法和多项式法相叠加的地表移动变形值计算模型，对于构筑物下煤层开采的安全性评价具有较高的实用价值.

1 概率积分法简介

1.1 方法特点

概率积分法的基础是随机介质理论[9-10]，按照其计算原理，共包含4个方面的基本假设：岩体为均质、非连续介质；具备线性叠加原理；弯曲带内岩体只发生形变，不发生体积的变化；开采结束后，地表的下沉体积等同于采区矿物的体积.

使用概率积分法对地表移动变形进行预计的过程为：将岩体看成特别小的颗粒介质，把颗粒按埋深高度不同分层划分，抽出下部颗粒，预测上部各分层中颗粒的移动规律，如图1.

图1 随机介质力学模型Fig.1 Stochastic medium mechanics model

假设颗粒之间完全失去联系，可以相互运动，当某一层的颗粒介质移动后，其上部的颗粒介质有向下移动的趋势，并伴有一定的概率，颗粒介质的移动将形成一系列反应，被影响到的颗粒介质都会产生相应的移动，最终将会影响到地表，引起地表的移动变形.

1.2 预计模型参数选择

地表移动变形预计模型包含计算模型的构建和输入参数选择两个方面.

1.2.1 预计模型将随机介质力学模型引入到煤层开采后的地表移动变形预计中，是将预计工作面的实际参数带入到最大下沉值公式中，预计煤层开采条件下地表各点的下沉值.如图2，以O1作为煤壁与采空区的分界线，当工作面推至煤壁O1点处时，采空区侧顶板冒落稳定后剩余自由下沉空间高度为W0(顶板弯曲下沉空间高度)，测得的地表最大下沉值也为W0，说明煤层开采达到充分采动.

图2 走向主断面地表下沉和水平移动Fig.2 Towards the main section surface subsidence and horizontal movement

根据随机介质理论，在X轴方向上任意点的地表下沉值和水平移动值表达式分别为：

(1)

(2)

式中,We(x)为X轴方向上任意点的地表下沉值，m；Ue(x)为X轴方向上任意点的水平移动值，m；r为主要影响半径，m；B为比例常数.

(3)

式中，H为走向主断面采深，m；tanβ为走向主断面主要影响角正切.

根据式(1)和式(2)，可绘制煤层开采后地表的下沉变化曲线和其对应的地表水平移动值变化曲线，如图3所示.

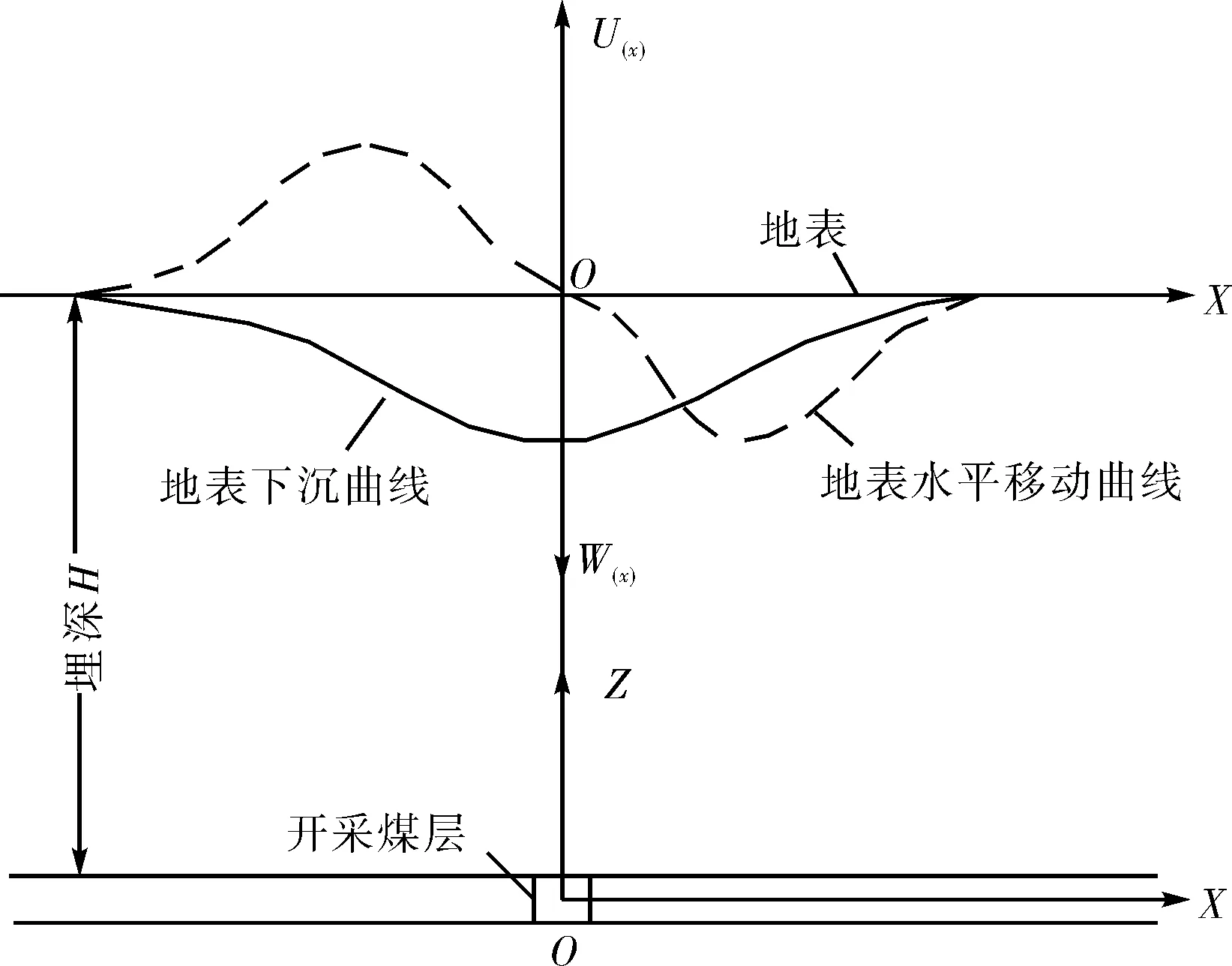
图3 地表下沉曲线和水平移动曲线Fig.3 Surface subsidence and horizontal movement curve

对走向主断面内坐标为x的地表任意点A，其水平变形值、倾斜值和曲率值由地表水平移动值和下沉值表达式在[0，+∞]区间的积分及其一阶或二阶导数进行计算，预计公式为：

(4)

式中，W(x)为计算点x的下沉值，mm；i(x)为计算点x的倾斜值，mm·m-1；K(x)为计算点x的曲率值，mm·m-2；U(x)为计算点x的水平移动值，mm；ε(x)为计算点x的水平变形值，mm·m-1；W0为最大下沉值，mm；M为采高，m；α为煤层倾角，°；q为下沉系数；b为水平移动系数.

1.2.2 输入参数根据公式(4)计算地表各点移动变形值所需的输入参数，可将其分为待采工作面的地质采矿基础参数和预计参数.其中工作面采高、煤层倾角为基础参数，工作面的最大下沉值、最大下沉系数、水平移动系数、开采影响传播角、主要影响角正切值、拐点偏移距和主要影响半径为预计参数.

基础参数选择依据待采工作面的开采设计可以得到，预计参数通常采用相邻工作面直接引用、同一矿区多个工作面均值处理后引用、不同矿区相同地质采矿条件下直接引用等工程类比法得到.

各主要预计参数的常规计算方法为：

1) 最大下沉值：最大下沉值依据该井田内相邻工作面的平均下沉系数，结合煤层倾角进行估算.

2) 水平移动系数：水平移动系数是煤层开采后地表最大水平移动值与最大下沉值之比，其值一般根据工程类比法得到，取值为0.3左右.

3) 开采影响传播角：开采影响传播角表示地表移动盆地向下山方向的偏移程度，主要用来确定下沉盆地拐点位置，与覆岩岩性、煤层倾角等因素有关.与煤层倾角的表达关系式为θ=90°-kα，其中α为煤层倾角，k与覆岩岩性相关(且为小于1的常数)，当工作面顶板覆岩岩性为坚硬时k为0.7～0.8，中硬时k为0.6～0.7，软弱时k为0.5～0.6.

4) 主要影响角正切值：主要影响角正切值是主断面边界采深与主要影响半径之比，与顶板上覆岩层的物理性质、采区尺寸、煤层倾角有关.

5) 拐点偏移距：拐点偏移距是自下沉曲线的拐点沿开采影响传播角作直线，与煤层相交的交点沿煤层方向到采空区边界的距离.

1.3 预计方法存在的不足

由上述计算公式和输入参数分析可知，概率积分法存在两个方面的不足：一是输入参数产生的误差，二是计算模型自身产生的误差.

1.3.1 输入参数产生的误差对于地表移动变形预计中需要输入的计算参数为采高、埋深、煤层倾角，开采影响传播角、主要影响角正切值、拐点偏移距、最大下沉系数、水平移动系数和任意点的坐标位置.其中采高、埋深、煤层倾角和两个参数均为工作面已知定值，任意点的坐标是预计不同位置所需输入的数值，也为定值，对于模型的计算结果不会产生误差.

待采工作面的开采影响传播角、拐点偏移距和主要影响角正切值均不能直接测量，主要由最大下沉值和水平移动值计算所得，而水平移动值的大小也与最大下沉值存在一定关系.最大下沉值是由下沉系数、采高和煤层倾角计算所得.对于待采工作面，其下沉系数需要通过工程类比得到，如果输入的计算参数不够准确，必然产生计算误差.

1.3.2 计算模型自身产生的误差由于概率积分法基于随机介质理论，计算模型中输入参数没有考虑待采工作面的岩性及组合特征，其计算结果中也必然会产生一定的误差.

2 主要预计参数确定方法的建立及预计模型修正

针对预计参数难以精准获取和计算模型自身存在误差问题[11]，通过实测结果与预计结果的误差原因分析，提出相对准确的预计参数确定方法，并对预计模型进行修正，为地表移动变形规律分析提供可靠的手段.

2.1 主要预计参数确定方法的提出

根据基于概率积分法的地表移动变形预计计算公式可知，最大下沉值选择的合理与否，直接影响着其它移动变形值的预计精度.为此，提出了覆岩剩余自由空间高度等于地表最大下沉值的观点，并基于剩余自由空间高度与冒高、采高和冒落带残余碎胀高度的关系，构建待采工作面最大下沉值的计算模型.

在采空区内，煤层开采形成的空间首先由顶板垮落岩层所充满[12]，然后冒落岩石在其上的裂隙带和弯曲下沉带的岩层重力作用下逐渐压实、高度逐渐缩小.冒落岩石初始高度与压实高度之差称之为覆岩剩余自由空间高度，即为地表最大下沉值.因此，地表最大下沉值的实质是地表在覆岩重力作用下能够向下移动的垂直距离，其大小等于覆岩剩余自由空间高度.

根据上述定义，只要计算出残余碎胀高度，根据采高，即可计算出地表最大下沉值.

W0=M-Hc，

(5)

式中，Hc为残余碎胀高度，m.

冒落岩体的残余碎胀高度计算公式为：

Hc=kiHm-Hm=(ki-1)Hm，

(6)

式中，ki为冒落岩体的残余碎胀系数，Hm为冒落带高度，m.

将式(6)代入式(5)中，得：

W0=M-Hc=M-(ki-1)Hm.

(7)

由于各岩层岩体的碎胀性系数和残余碎胀性系数不相同，为了得到煤层开采后冒落岩体被压实后的高度，首先要对冒落岩层发育的最高层位和最高位置进行判定，然后根据各个冒落岩层的高度和各个岩层岩体的残余碎胀性系数，才能求得冒落岩体被压实后的高度.

2.2 预计模型修正

为了削减计算误差，根据相邻工作面的实测数据，设想从最大下沉值的计算模型入手，在最大下沉值计算模型之后增加一修正函数项f(x)，对各移动变形值的预计进行修正，即采取多项式法进行修正[15-16].

具体方法是根据实际测量多个工作面的下沉值与预计结果的下沉值之间的差值，将多个差值的计算结果取平均值，对最终的均值曲线采用MATLAB软件拟合成对应的函数公式，添加到基础参数修正后的下沉值预计结果中，完成概率积分法的下沉值计算模型修正.

下沉值的计算模型修正后如式(8).

Wxz=Wyj+f(x),

(8)

式中，Wxz为修正后的预计下沉值；Wyj为概率积分法基础参数修正后的预计下沉值；f(x)为修正项.

根据下沉值的多项式修正模型在[0，+∞]区间的积分及其一阶或二阶导数进行计算，得到其它变形值的多项式修正计算模型.

倾斜值为下沉值的一阶导数，得到倾斜值为：

(9)

曲率值为下沉值的二阶导数，得到曲率值为：

K(x)=W″xz=W″yj+f″(x)=

(10)

由水平移动值根据与倾斜值之间的比例关系，得到水平移动值为：

(11)

由水平变形值与曲率之间的比例关系，得到水平变形值为：

(12)

根据各移动变形值的计算公式和修正后的计算公式、以及其一阶导函数f′(x)、二阶导函数f″(x)，结合地表最大下沉值的计算公式，得到修正后的各变形值计算公式[17-19].

(13)

将上述公式中的二维模型转化为三维地表移动变形值计算模型，即可求取地表受采动影响的各变形值.

3 现场实测验证分析

3.1 现场实测

以某矿S2S2工作面测点布置为例，沿工作面推进方向中线位置布置一条观测线，测线距进回风巷道的垂直距离均为113.5 m，共计34个测点，间距为30 m，其中1号测点距切眼2 m，如图4所示.

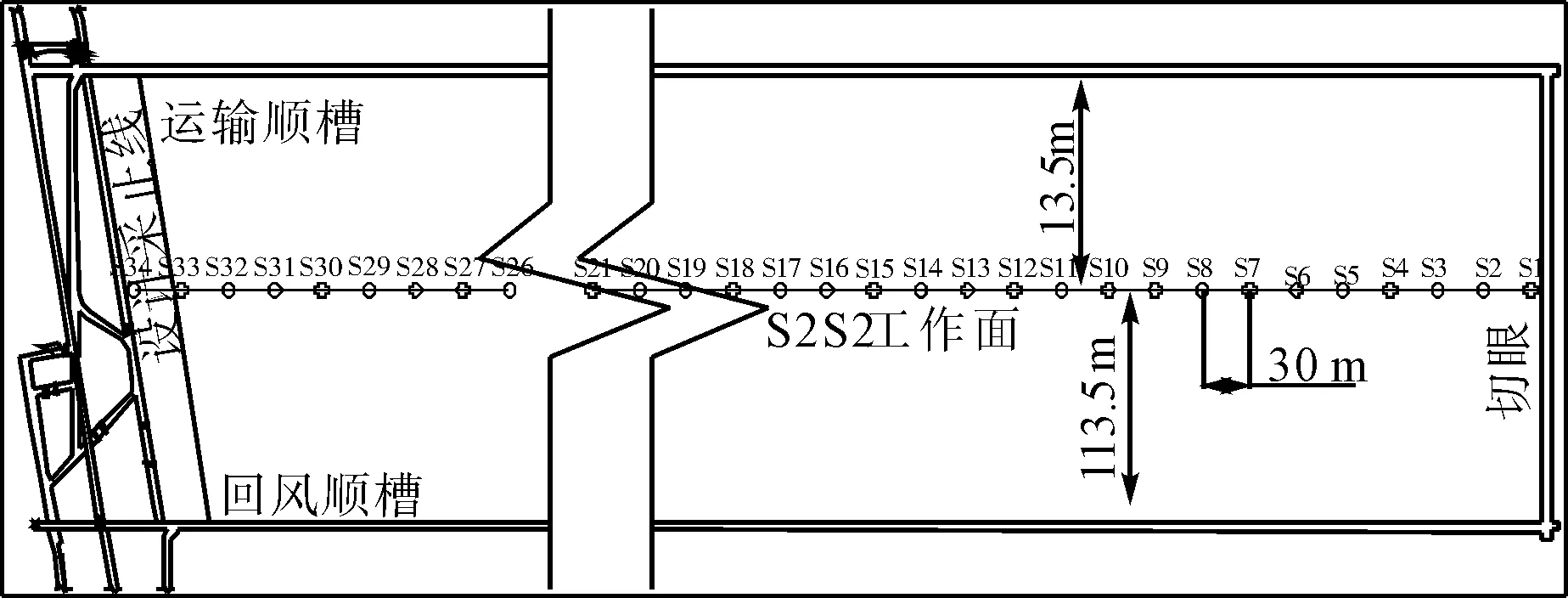
图4 工作面测点布置示意图Fig.4 Diagram of measuring point arrangement in working face

当工作面回采结束后，工作面上覆地表中各测点连续6个月内累计下沉值小于30 mm时，即认为地表移动变形结束，工作面达到充分采动[20].测点1至测点34的移动变形值如表1所示.

表1 各测点的地表移动变形实测值Tab.1 Actual measured values of surface movement and deformation at each measuring point

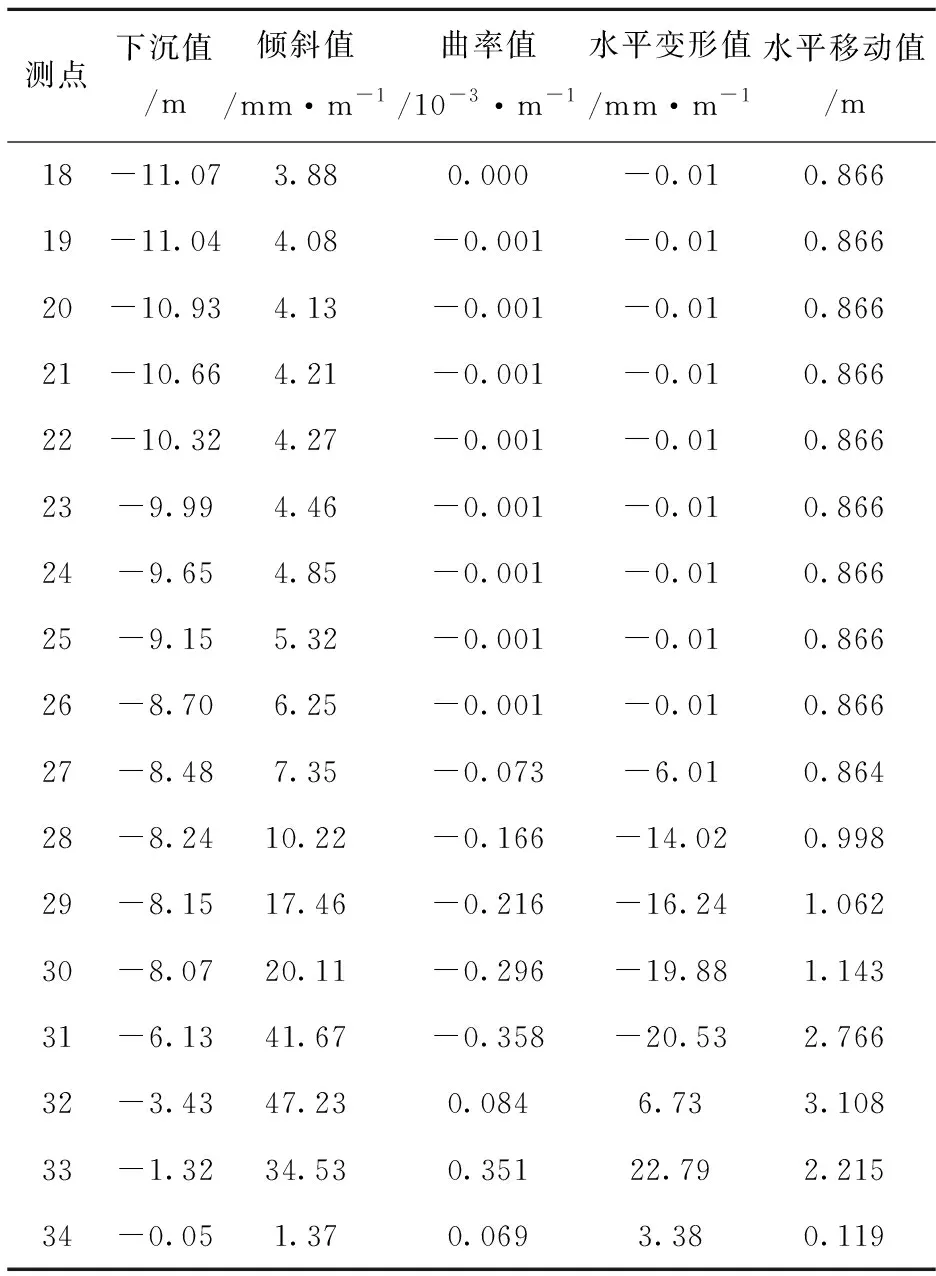
续表1

3.2 多项式修正项f(x)计算

f(x)是由各测点实测下沉值与预计下沉值之间的差值求取，以该矿S2S2、N1S3、S2N1、N1S1共计4个综放工作面为例，将预计结果与实测做差值，各差值的结果求取均值，将均值曲线利用MATLAB软件回归拟合，差值曲线图如图5.

图5 4个工作面各测点实测下沉值与预计值之间差值曲线图Fig.5 Curve of the difference between the actual measured subsidence value and the predicted value at each measuring point of four working faces

由于曲线具有微小的双波峰、微小的双低谷和中间平滑的特性，采用一般多项式拟合线性关系较差，因此，选用MATLAB中三角函数算法对均值曲线进行拟合，得出系数等级为7次，R2为0.996 8，拟合精度较高.拟合的曲线如图6所示.

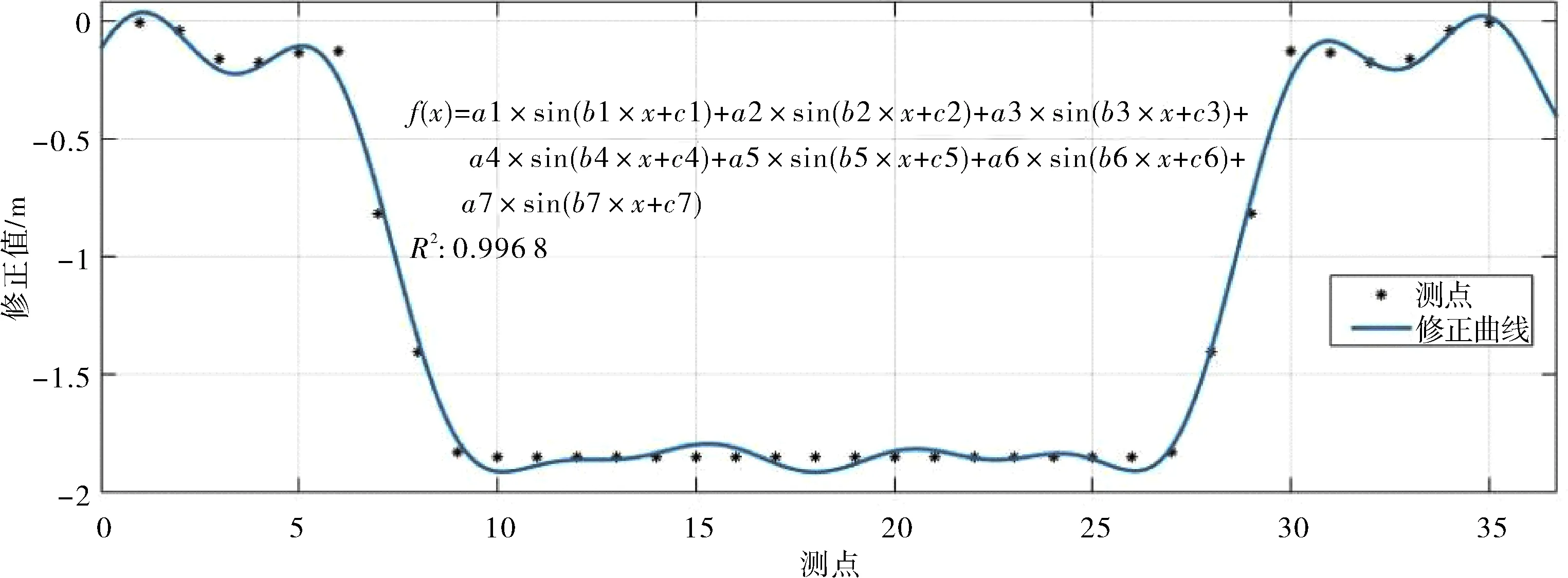
图6 下沉值差值的均值拟合曲线图Fig.6 The mean fitting curve of subsidence difference

f(x)=1.899sin(0.08489x+3.179)+0.1936sin(0.7251x-2.12)+0.2275sin(0.4684x-0.6443)+0.9147sin(0.3432x+1.774)+0.966sin(0.3165x-0.9018)+0.8867sin(1.186x-0.9285)+0.8808sin(1.203x+1.907).(14)

按照上述计算方法计算得到4个综放工作面的下沉值，绘制下沉曲线对比图(图7).

由图7可以看出：利用多项式法修正后的计算模型预计已采工作面的下沉值与实测数据进行对比，下沉值的误差范围仅为0.1～0.4 m，极大的减小了由计算模型自身带来的预计误差，修正效果较好，能够精准预计该井田内煤层开采带来的地表移动变形.

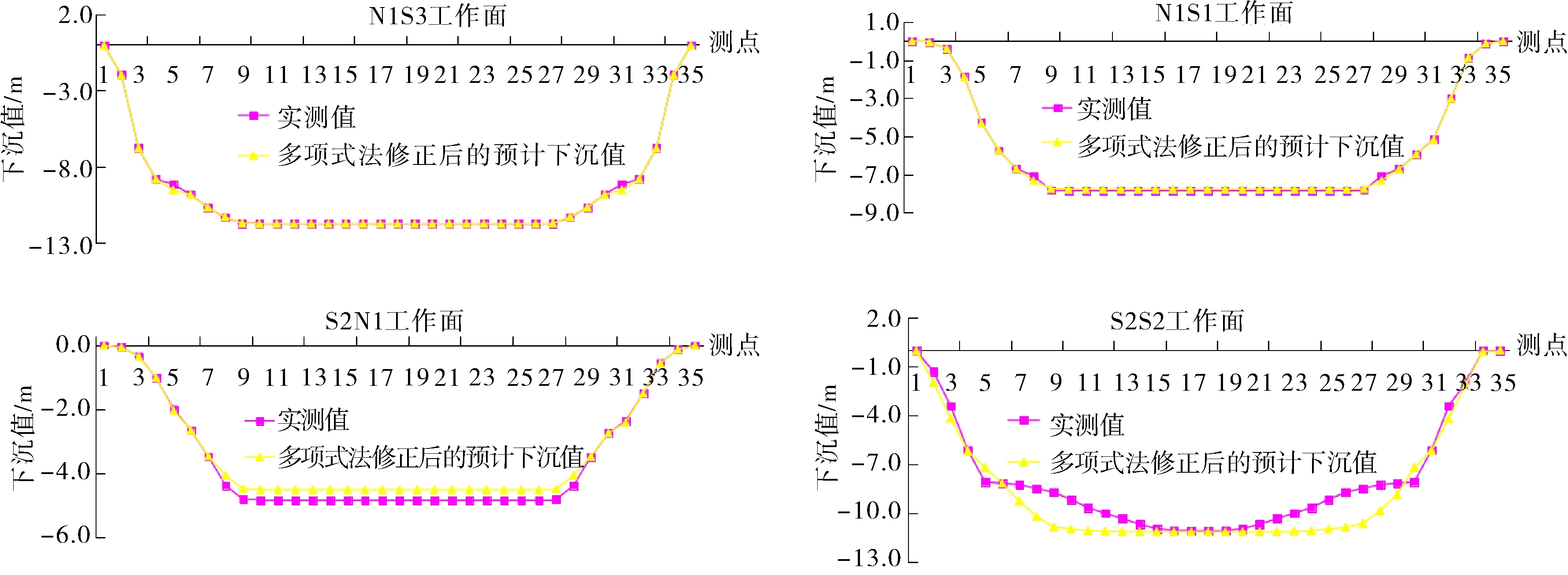
图7 综放工作面实测下沉值与修正预计下沉值对比图Fig.7 Contrast chart between actual measured subsidence value and revised predicted subsidence value of each mechanized caving face