涡旋光干涉衍射综合试验仪的设计与制造
2022-10-20杨佳辉张子睿顾子健张云哲
杨佳辉,张 艳,肖 晗,张子睿,顾子健,张云哲
(1.西安石油大学 理学院,陕西 西安 710065;2.西安文理学院 机械与材料工程学院,陕西 西安 710065)
光学涡旋(Optical Vortex,OV)是30多年前Coullet等人建立起的概念,OV的奇特性质使人们对一些物理现象有了不同以往的认识,其中包括自旋—轨道相互作用、玻色—爱因斯坦凝聚物等。OV携带轨道角动量(Orbital Angular Momentum,OAM),具有可调控的自由度,在实际应用中也有广阔的前景,例如光通信、光镊、信息加密、天文学等[1-4]。在现有的光电本科专业及相关本科专业中,近代经典光学实验在光学实验中学习较多,而对于光学科研方面接触较少。随着社会的高速发展,专业性人才需求量不断增加,因此将OV基本实验引入本科实验教学中,符合当下学生对科研、工作等方面的需求。
经过市场调研发现,OV综合实验仪器在市场中并不常见,非OV光学综合实验仪器所占市场比重非常大,且价格高昂。本项目中的光学综合实验仪所用到的附件为常见的透镜、反射镜、滤波器、分束镜等光学元件,价格低廉;将多项实验光路整合成综合实验仪器可以提高光学元件的利用率,降低实验成本。
1 基本原理
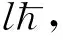
本实验仪采用拉盖尔—高斯光束,拉盖尔—高斯光束是典型的OV,它是圆柱坐标系求解傍轴亥姆霍兹方程的解[5,6]。
在傍轴条件下亥姆霍兹方程表示为:
(1)
使用分离变数法,可求解出拉盖尔—高斯光束的电场分布为:
(2)
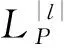
1.1 OV的产生[7-9]
本项目实验仪采用螺旋相位板(Spiral Phase Plate,SPP)来产生拉盖尔-高斯光束。
SPP的一端为平面,另一端为螺旋面,入射光束从平面端入射,从螺旋面出射得到目标光束,设出射光的在SPP上的方位角为φ,则在此方位角φ上的相位改变因子E为
E=e-ilφ
(3)
其中
(4)
hs是螺旋相位板的步幅高度,n是螺旋相位板折射率,n0是周围介质板折射率,λ是入射光的波长,l是拓扑荷数。
对于拉盖尔—高斯光束,SPP产生的总相位延迟为2πl,l必须为整数,从公式(4)得到SPP厚度hs必须为
(5)
如果SPP厚度hs不满足公式(5),出射光会存在缺陷,在实验上会观察到光环具有缺口,出现拓扑荷数l为分数的现象。
SPP产生的拉盖尔-高斯光束具有转换效率高、方便实验仪搭建光路的优点,但缺点也比较明显,只会产生特定的拓扑荷数,不能很好的控制OV参数。
2.2 OV干涉分析[10]
① OV与平面波干涉
OV复振幅公式可表示为
E1=A1eilφ
(6)
平面波复振幅公式为
(7)
其中A2为振幅,使A1=A2=A12,设A12为常数,干涉后的复振幅公式为
(8)
光强分布
(9)
② OV与球面波干涉
球面波复振幅公式为
(10)
其中A1=A3=A13,设A13为常数。球面波与OV干涉后的复振幅公式为
(11)
光强分布由公式(9)计算,有
村长呃你屁股坐在哪边边,怎么老替他们说话,你应该帮我讲话。我投了你的票的,你是我的村长,我是你的村民。
(12)
2 实验仪的设计方案
干涉系统的设计:利用空间滤波器、扩束准直系统得到平面波,使用可拆卸的分束镜将光分为两束,一束经过SPP转换为OV,另一束仍为平面波,在分束镜中两者发生干涉,从而实现OV与平面波的干涉。OV与球面波的干涉只需在分束镜分束后的平面波光路添加可拆卸的孔径结构即可。OV的杨氏双缝干涉只需拆掉分束镜,在SPP后安装可拆卸的杨氏双缝即可,并在接收端用CCD接收干涉条纹,进行特性分析。
衍射系统的设计:只需将杨氏双缝干涉的双缝进行调整,将双缝切换成单缝衍射元件,接收端即可用CCD接收到衍射条纹[12-15]。
轨道角动量检测系统的设计:本项目将采用圆孔衍射的方法进行检测,使用衍射系统得到圆孔衍射条纹,以分析涡旋束的轨道角动量。
实验仪也可以对SPP系统进行调整,用来产生普通激光的干涉、衍射实验现象[16]。
3 实验结果
3.1 OV模式模拟图
图1表示不同阶数的LG光束光强分布图。可以明显看出随着拓扑荷数的增大光强中心暗斑增大,圆环也相应地逐渐变大,并且当p不为零时,圆环个数也随之变化。

图1 不同模式的LG光束光强分布图
从图1第一行表示LG光束的径向模式p=0时,并且拓扑荷数l分别为1,2,3时的光强分布。从图中可以看出光强的横截面分布是中心为暗斑的一个圆环,由于相位奇点的存在,所以光强中心都为暗核。随着拓扑荷数的增加,圆环半径也随之增加,这是因为光束的扩散速度与拓扑荷的阶数有关。因为当l增大时,代表奇点的不确定性增大,奇点周围区域的光强受到奇点不确定性的影响就会越明显,从而导致奇点周围的暗区域面积增加,即就是环形光斑的半径增大。
当LG光束的径向模式p=1和p=2时,发现横截面光强分布不再是一个圆环,而分别是两个和三个光强强度分布不同的圆环,如图1第二行和图1第三行所示。因为当径向位置r从零逐渐增加时,会经历LG光束的p个径向模式(也称为过零节点)。过零节点指的是此处的光强能量为零,主要归因于沿半径方向的位相由于径向模式p的存在会发生突变,每次位相突变值为π,并且在突变处的位相是不确定的,此处的能量为零。
从图1的第二、三行可以看出,横截面径向圆环个数由拉盖尔多项式的径向模式p决定,并且圆环的个数等于p+1,即p=0时,圆环个数为1;p=1时,圆环个数为2;p=2时,圆环个数为3。当p=0时,光斑为一个光环;当p=1,2,3时,光圈的个数在增加的同时,外围光环半径也在增大,光斑的半径是同时增加的。从图中也可观测到圆环的光强能量主要分布在主环上,即最内侧的圆环上,而外围的圆环的光强能量越来越小,表示能量随着拓扑荷数和径向模式数的增加变得发散。在理想情况下,根据能量守恒定律,主环上的光强能量也有所下降,将少部分的能量转移到外围圆环上。
3.2 OV与平面波干涉
一般情况下,两束等振幅的光发生干涉后的光强取决于两束光的相位差。讨论的涡旋光束、平面波和球面波的振幅是相等的,且涡旋光束的拓扑荷数为1。当涡旋光束与平面波在自由空间发生干涉时,由于平面波的波前是平面的,会导致接收光屏各点的相位差相当于涡旋光束的相位减去一个常数,相位差的分布与涡旋光束在接收光屏上的相位分布是相似的,在相位差取余弦后,就会得到分叉数为1的叉形干涉条纹,且旋转涡旋光束不会改变干涉条纹的分布如图2所示。
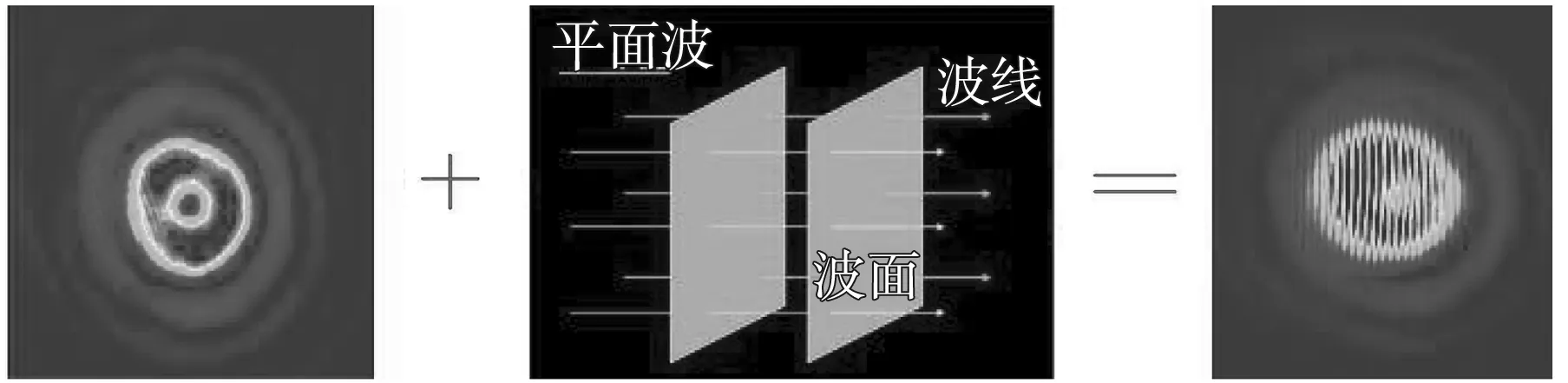
图2 一阶LG与平面波干涉实验图
3.3 OV与球面波干涉
当涡旋光束与球面波在自由空间发生干涉时,球面波在接收光屏上的相位分布呈圆环状,再考虑涡旋光束在接收光屏上的相位分布后,其得到干涉条纹为一个螺旋形,且转动涡旋光束不会影响螺旋形的绕向如图3所示。

图3 一阶LG与球面波干涉实验图
4 实物示意图
本综合实验仪作为创新型、综合型、研究型、组装式的光学实验系统如图4所示,其优势主要体现在以下几方面:

图4 涡旋光干涉、衍射综合实验仪
第一点,本综合性实验仪集光、机、电、计算机技术于一体,在满足一般激光实验的基础上加入涡旋光干涉衍射等实验。
第二点,本实验仪既满足本科普通物理实验的基本要求,又能够锻炼学生的实验操作能力。学生可以自行灵活的组合、装配、调试实验装置,来完成更多不同的实验,利用软件进行理论与实验结果的拟合,具有一定的科学研究性质,更具有灵活性、综合性、研究性和设计性。
第三点,本实验仪将干涉,衍射,偏振等实验集成到同一实验平台上,既节约空间,又降低成本。本实验仪相比于市场上其他公司的光学综合性实验仪器,价格低廉,能够有效节省购买实验仪器的经费以及储存实验仪器所需的空间,更加符合高校物理实验室的基本要求,综合来看具有较高的市场潜力。
5 结 语
本文设计的涡旋光干涉衍射综合实验仪在固定光路的情况下,各个器件可以进行微调,既锻炼了学生的动手能力又减少组建光路的时间,有效提升效率。将四种实验光路融合在一个实验台上,大大节约光路空间。
