弹塑性问题的改进无单元Galerkin方法计算软件开发
2022-10-20张明哲彭妙娟程玉民
张明哲,彭妙娟,程玉民
(上海大学 力学与工程科学学院,上海 200444)
0 引 言
在求解高速碰撞、动态裂纹扩展和材料几何非线性等问题时,无网格方法可以基于一系列离散的节点构造试函数,从根本上避免采用有限元法容易发生的网格畸变、计算过程终止等缺点。无网格方法受到越来越多国内外学者的关注,因此开发一款以开放式语言为基础的无网格方法计算软件很有必要。
有关弹塑性问题的无网格方法软件开发起步较晚,现阶段比较完善且运用广泛的工程分析软件仍然是有限元法软件,如MSC Nastran、Abaqus、Ansys、MIDAS等。Nayroles等基于移动最小二乘法提出扩散单元法,无网格方法才真正发展起来。王宇新等开发无网格MPM法三维前处理系统;张征等开发接触力学自适应无网格计算系统,求解二维弹塑性接触力学;ABBASZADEH等开发一种无网格数值程序模拟地下水污染方程;曾清红利用并行计算技术进行适于无网格方法的并行插值算法研究;NAKATA等提出一种在图形处理单元上的基于径向点插值方法的无网格分析并行算法;SINGH等基于Fortran语言开发并行算法,实现传热和流体流动问题的无单元Galerkin方法的并行求解;LIU等使用MLS为无网格方法开发一种基于背景网格的自适应程序;文建波等开发基于Delaunay三角化的无网格方法计算结果后处理软件。此外,Ansys作为成熟的有限元软件,已经内置无网格计算方法的模块。
关于弹塑性问题的无网格方法的研究,传统无网格方法采用移动最小二乘法构造试函数,在计算过程中容易形成病态或者奇异方程组,而弹塑性问题的求解要求布置足够多数量的节点以提高计算精度,这严重影响计算效率和精度。为解决这些问题并扩大无网格方法的应用范围,CHEN等应用复变量重构核粒子法,用一维基函数形成二维问题的校正函数解决二维弹塑性问题;CHENG等使用可直接施加边界条件的插值移动最小二乘法获得形函数,提出插值无单元Galerkin方法解决二维弹塑性问题;CHENG等采用罚函数法应用本质边界条件解决二维弹塑性问题,获得更高的计算精度和效率;MENG等利用维数分裂法将三维波动方程分解为二维问题,推导改进的插值维数分裂无单元Galerkin方法求解三维波动方程;蔡小杰等采用移动最小二乘法建立弹塑性大变形问题的改进的无单元Galerkin方法;DENG等基于改进的复变量无单元Galerkin方法提出二维非线性的弹塑性问题的数值模型;WU等、PENG等和ZHENG等提出改进的无单元Galerkin方法解决弹塑性大变形问题,利用Galerkin积分弱形式建立求解方程,其形函数满足Kronecker函数的性质,可直接施加本质边界条件,并提出采用插值无单元Galerkin方法求解三维弹塑性问题,可极大地提高计算效率和精度,由其编写的无网格方法部分程序算法,可极大地减少计算量。
上述关于弹塑性问题的无网格方法的程序大多不具有全流程分析(精确的计算运行程序和可视化的前、后处理程序),如MATLAB专注于计算程序,使得分析问题时不能在一个软件中兼顾建模、计算分析和结果展示,也间接阻碍弹塑性问题无网格方法的普及和应用。无网格方法的相关软件很少有关于弹塑性分析的。
本文开发弹塑性问题的改进无单元Galerkin方法软件,包括前处理程序模块、计算程序模块和后处理程序模块3个部分。前处理程序链接Gmsh建模,可以获得节点信息等信息流,然后通过弹塑性问题的改进无单元Galerkin方法计算程序进行数值模拟,最后利用后处理程序模块实现数值结果的可视化。
1 软件架构
该软件基于C++编程语言开发,依托改进的无单元Galerkin方法解决弹塑性问题,能够高效直观地建模并进行准确的受力分析。软件面向的对象包括节点、单元以及边界条件等模型数据,对其进行计算分析后得到处理结果,最后将结果在软件上以可视化界面进行显示,即前处理程序、分析计算程序和后处理程序3个部分。前处理程序、计算程序和后处理程序不是互相独立工作的,其数据联系流程见图1。

图1 软件流程图
前处理程序模块主要为建立模型和节点生成:基于OpenGL库直接使用C++语言进行建模,输入参数,预处理必备的结构参数值。因无网格方法需要节点进行函数拟合,其中的关键环节是对计算域离散剖分并获取节点信息。无网格方法将计算域离散为一系列点,根据边界法向前推进,在计算域内部进行填充式布点,同时利用Delaunay算法进行网格筛选以获得节点信息。无网格方法分析计算部分首先根据建模的维度选择二维弹塑性或三维弹塑性问题的改进无单元Galerkin方法的程序,将计算得到的数据传递给后处理模块,后处理模块主要显示结果。
前处理程序模块需要输入模型的几何信息和物理信息,包括各种属性和边界参数等,建立分析模型后对模型进行节点处理。前处理的重点是得到节点信息并读入模型节点数据,为无网格方法分析做准备。
本软件链接简单的CAD引擎,通过编程先设定模型所需的主要节点,连点成线,然后生成面,最后生成体。每个点、线、面和体都有唯一的标签。程序可直接输入各种几何信息和物理信息,提供所需的各种属性和边界参数,如载荷大小以及坐标、边界条件等。
计算程序模块进行无网格方法的计算,最主要的是矩阵计算和求解。
后处理程序模块对每个单元建立单元节点位移向量。以文件形式读入前处理获得的节点几何信息和网格信息等,将计算程序得到的位移输入到后处理的坐标修正程序,通过改变节点和网格的坐标值显示模型的变形量,从而实现模型变形的可视化。
2 前后处理程序模块
2.1 前处理程序
前处理是数值计算中非常重要的环节,不仅决定着程序解决问题的通用性,而且直接影响后续数值计算的精度和效率。前处理过程首要的是布置节点,包括节点编号及相应的坐标值。节点数据的空间位置信息定义为类P_Point,其C++程序如下。
class P_Point
{
public:
P_Point(const double x = 0,const double y = 0,
const double z = 0):_x(x),_y(y),_z(z) { }
~P_Point() { }
const double get X() const { return _x;}
const double get Y() const { return _y;}
const double get Z() const { return _z;}
void set X(const double x) { _x = x;}
void set Y(const double y) { _y = y;}
void set Z(const double z) { _z = z;}
bool operator <(const P_Point&p) const;
protected:
double *Point_p;
double _x,_y,_z;};
节点数据的获取采用coord的vector容器接收。节点的初始三维空间信息存储在vector容器中,每3个连续数据为1组。为方便使用,按照节点排布顺序重新存储数据,其coord的C++程序如下。
std::vector
P_Point p;
for (int i = 0;i { double x = coord[i]; double y = coord[i + 1]; double z = coord[i + 2]; p = P_Point(x,y,z); nodes.push_back(p); } 前处理分为3个部分:使用C++编程建模;输入材料的各要素数值,如截面形状及大小、载荷定义等;生成无网格方法分析所需要的节点数据。 在无网格方法前处理程序中,链接OpenGL库直接使用C++语言建模,输入各种几何信息和物理信息,对模型信息属性和边界进行配置,以便建模成功后生成网格。网格应进行合适性判断,减少节点距离过近、避免出现丢失边界及穿透边界的情况,再通过边交换方法对三角形进行优化,提高三角形质量。 在求解域中选取适当分布的离散节点,根据一定的准则进行筛选以形成适合计算的结构。以二维问题为例,需要先确定一个点为中心点,再根据距离准则筛选出一定数量的卫星点,在这些卫星点中运用Delaunay准则进行临时三角化处理,遍历找出最合适的点云结构,最后采用改进的移动最小二乘法进行节点数据处理。 后处理程序读取前处理的节点、单元等信息,获取计算程序得到的位移等信息,并重新组织成标准后处理结果文件的形式,利用计算机可视化技术再现模型信息,将分析结果以图像形式显示出来。 本系统的后处理程序包括数据处理程序、图像显示程序等,具体内容包括3个部分:(1)模型数据(初始的节点编号、坐标等信息,以及计算程序得到的数据)的提取;(2)模型结果可视化处理,分析结果数据,重新构建模型的计算结果视图;(3)结果数据查看,利用Visual Studio软件的文件流函数将生成的数据直接存入文本文件。 前处理和计算程序产生的结果数据通常包括模型数据和结果数据,后处理程序采用文本文件存储以上信息。文件接收网格节点等信息,并将其存储到文本文件中,同时改变节点的空间坐标以达到将变形可视化的目标。文本文件网格节点等信息修正、显示位移的操作程序如下。 //进行文件操作 int _total = getFileLine("*****");//获取文件 总行数函数 int Nodes_row=getStrrow("*****","*****"); //获取某文件的某一指定字符串的行数 ifstream fin("*****"); if (!fin) // 如果读取失败,打印fail { cerr <<"fail" < return; } ofstream fout("*****.txt");//创建一个新文件接收字符串 string s; int _index = 0; float data; while (getline(fin,s)) { if (_index <= Nodes_row || _index >= EndNodes_row) fout < else{ istringstream iss(s); vector while (iss >>data) { newdata.push_back(data); } bool is_chuan = false; int _L = newdata.size(); if (_L == 3){ double chuandi = dataprocess(newdata[0], deformedpoint); fout < else fout < _index++;} 采用基于点的近似构造逼近函数是无网格方法的关键。形成逼近函数的主要方法有光滑粒子法、移动最小二乘法和重构核粒子法等,其中移动最小二乘法应用最为广泛,即 (1) 式中:为基函数的个数;()为基函数;()为待定系数。线性基函数 =[1] (2) 点邻域内的局部逼近为 (3) 定义泛函数 (4) 式中:为点影响域内的节点;为影响域覆盖点的节点数;(-)为定义的权函数。 ()=()() (5) 其中: ()=() (6) ()=() (7) 由以上计算可得逼近函数 (8) 式中:()为形函数, ()=[()() …()]= ()()() (9) 在移动最小二乘法中,当较大时,式(5)有时是病态的甚至是奇异的,难以获得正确解或者难以求解。由此,采用改进的移动最小二乘法,选取正交函数作为基函数,得到的方程不但可以避免病态和奇异,而且不需要求解方程的逆,可直接得到该方程组的解 ()=()(), (10) 其中: (11) 将式(10)代入式(3),可得 (12) (13) 改进的移动最小二乘法求解系数()时不需要求解矩阵()的逆,可避免出现的病态或者奇异的方程组,因此可提高计算效率和精度。 基于改进的移动最小二乘法推导出二维弹性大变形问题和三维弹塑性问题的改进无单元Galerkin方法的方程。三维问题可囊括二维问题相关公式,对三维公式推导的介绍更具有代表性,所以此处只介绍三维弹塑性问题的方程推导过程。 弹塑性问题的平衡方程可表示为 (Δ)+Δ=0,∈, (14) 式中:(·)为微分算子矩阵;Δ为域内任一点的应力增量;Δ为域内任一点的体力增量。 (15) Δ=[ΔΔΔΔΔΔ] (16) Δ=[ΔΔΔ] (17) 弹塑性问题的几何方程表示为 Δ=(Δ) (18) 式中:Δ为影响域内任一点的应变增量;Δ为影响域内任一点的位移增量。 弹塑性问题的物理方程表示为 Δ=Δ (19) 在弹性阶段内和塑性阶段内表达式不同。 定义边界条件为 (20) (21) 在采用改进的无单元Galerkin方法求解弹塑性问题时,需要使用适当的方法将求解问题线性化,即使用一系列的线性解逼近非线性问题的解,例如采用逐步增加载荷的方法,按比例施加载荷。 由改进的移动最小二乘法的形函数表达式可得,域内任一点的位移增量向量可表示为 (22) 式中:为点影响域内的节点数。 应变张量可表示为 (23) 综合上述推导,可得 (24) 对表达式进行替换,可得 (25) (26) (27) (28) (29) 若在应力边界上点处作用集中力,则 (30) 式(26)可转化为 (31) 3.3.1 数据处理 模型进行数值计算一般需要3类数据,分别为节点数据、单元数据和边界条件数据。 节点数据主要包括节点的空间信息、编号,以及其对应的计算得到的位移等数据。 单元数据主要包括定义的材料特性(如弹性模量、泊松比和密度等相关信息)和物理特性(主要是几何参数)。 边界条件数据主要用以分析对象与外界的相互作用,主要包括位移约束和载荷条件。位移约束数据规定节点在自由度上所受到约束限制,载荷条件数据用于定义模型中节点载荷等力作用的位置、方向和大小。 同时,因为计算程序中的数值计算大多为矩阵运算,所以建立矩阵类class Matrix以及稀疏矩阵类class SparseMatrix,程序如下。 class Matrix { public: Matrix(); Matrix(int,int); Matrix(const Matrix &m); Matrix(int,int,double);//预分配空间 virtual ~Matrix();//析构函数 Matrix&operator=(const Matrix&);//矩阵的复制 int row() const; int col() const; private: int rows_num,cols_num; double **p; void initialize();//初始化矩阵 }; 矩阵类中部分函数定义如下。 double Point(int i,int j) const; //求矩阵的逆矩阵 static Matrix inv(Matrix); //矩阵加法 Matrix&operator+=(const Matrix&); //矩阵减法 Matrix&operator-=(const Matrix&); //矩阵乘法 Matrix&operator*=(const Matrix&); //求K矩阵 Matrix&Kjuzhen(Matrix,Matrix); class SparseMatrix { int nrLines,nrColumns; int nrElements;//非零元素数量 double* elements;//三元组的值存放 int* lines,*cols;//三元组的坐标 public: SparseMatrix(); SparseMatrix(int,int,double*,int*,int*); SparseMatrix(int,int,int,double*,int*,int*); SparseMatrix(const SparseMatrix&); ~SparseMatrix(); int getNumberOfLines(); int getNumberOfColumns(); int getElement(); } 稀疏矩阵中的部分函数如下。 friend SparseMatrix operator+(const SparseMatrix&,const SparseMatrix&); friend SparseMatrix operator-(const SparseMatrix&,const SparseMatrix&); friend SparseMatrix operator*(const SparseMatrix&,const SparseMatrix&); friend SparseMatrix operator*(const SparseMatrix&,double) 这些函数实现计算程序全部的矩阵运算,对矩阵的各种操作进行封装,能大大提高计算效率。 3.3.2 数值流程 弹塑性问题的改进无单元Galerkin方法的数值计算流程如下。 (1)对结构视为完全弹性,施加全部载荷进行计算。 a.遍历循环每个网格,对网格内的高斯积分点进行循环,判断高斯积分点是否在域内,是则进行以下步骤,否则结束循环;确定高斯积分点影响域内的节点,然后计算积分点处的形函数及其导数;用式(30)计算等效刚度矩阵,保存该积分点对矩阵及等效节点载荷的贡献; b.结束网格循环,得到刚度矩阵和等效载荷列向量Δ的第一项; c.进行边界积分运算,用类似方法计算等效载荷列向量Δ的第二项; d.由第一项和第二项计算Δ; e.拟合各节点的位移、应力和应变等信息。 (3)施加载荷增量Δ; (4)按照式(25)计算刚度矩阵,要保证在弹性阶段和塑性阶段分别采用不同公式进行计算; (5)求解式(30),得到所有节点的位移增量,进而计算应变增量和应力增量,并把位移增量、应变增量和应力增量叠加到加载前的数据上; (6)若加载到全部载荷,则跳出循环; (7)输出节点的位移。 对二维和三维受集中力的悬臂梁采用弹塑性问题的改进无单元Galerkin方法进行弹塑性大变形数值分析。对悬臂梁建模,利用前处理程序模块在求解域中布置节点,并将节点信息输入到编写的C++数值算例程序,计算获取节点处的位移和应力、应变数据,并将计算结果与使用MATLAB软件得到的数值解进行比较,验证改进无单元Galerkin方法以及程序的有效性。 自由端受集中力载荷的二维悬臂梁示意见图2。梁的几何尺寸为=8 m,=1 m,载荷=1 N,泊松比=0.25,屈服极限=25 Pa。材料的弹性模量为=1.0×10Pa,按平面应力问题求解。 图2 受集中力的二维悬臂梁示意 采用前处理程序布置节点,结果见图3。 图3 二维悬臂梁节点分布 采用弹塑性问题的改进无单元Galerkin方法进行计算,将获得的位移信息输入后处理程序中,悬臂梁的变形见图4,其位移量增大30倍。 图4 二维悬臂梁变形 为验证程序的准确性,将本文程序计算得到的数值解与MATLAB结果进行对比,见图5。本文二维计算程序能够得到满意的结果。 图5 二维悬臂梁的节点位移计算结果对比 自由端受集中力载荷的三维悬臂梁示意见图6。梁的几何尺寸为=8 m,=1 m,=1 m,其他材料特性与第4.1节相同,本文案例可采用线性强化弹塑性模型和MISES屈服准则。 图6 受集中力三维悬臂梁示意 采用前处理程序布置节点,结果见图7。将计算得到的数据输入后处理程序中,模型的变形结果见图8和9,其位移量增大15倍。 图7 三维悬臂梁节点分布 图8 三维悬臂梁实体变形 图9 三维悬臂梁节点变形 将本文程序计算得到的数值解与MATLAB结果对比,见图10。本文软件的三维计算程序能够得到满意的结果。 图10 三维悬臂梁的节点位移计算结果对比 采用C++语言开发弹塑性问题的改进无单元Galerkin方法计算软件,实现快速建模和对离散点集进行前处理后的数据采集,采用改进无单元Galerkin方法的程序计算结果,将得到的节点信息和边界条件等信息以文件形式输入到后处理程序中,实现结果图形可视化。通过数值算例分析,验证本文方法的有效性和优越性。 在后续工作中,在前处理程序中将加入更多程序模块,完善模型的边界条件处理和组件功能等程序;计算程序模块将加入弹性大变形和弹塑性大变形等问题的计算程序,以支持复杂问题的数值分析,为形成完善的无网格方法计算软件奠定基础。2.2 后处理程序
3 计算程序
3.1 改进的移动最小二乘法




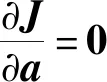


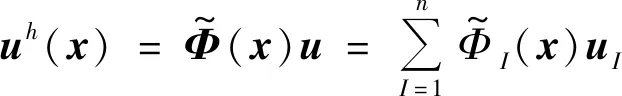
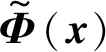


3.2 弹塑性问题的改进无单元Galerkin方法
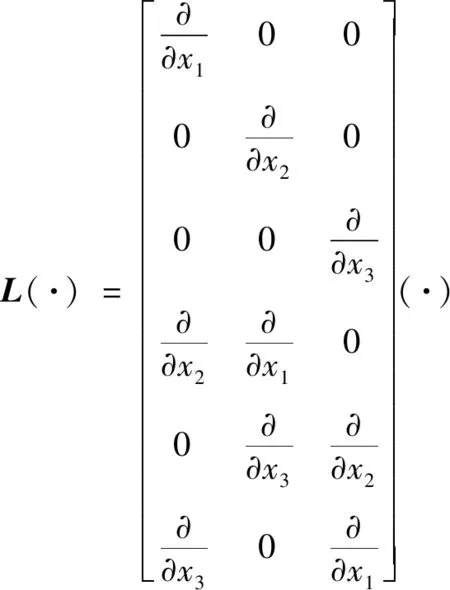

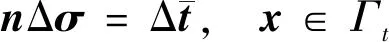







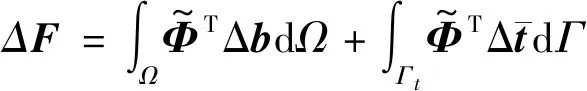






3.3 弹塑性问题的改进无单元Galerkin方法计算程序开发

4 数值算例
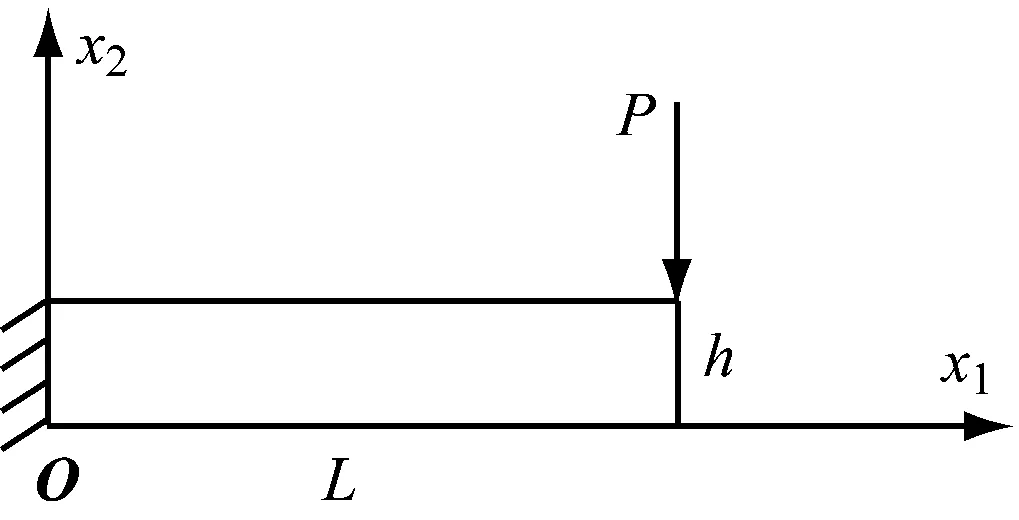
4.1 二维算例



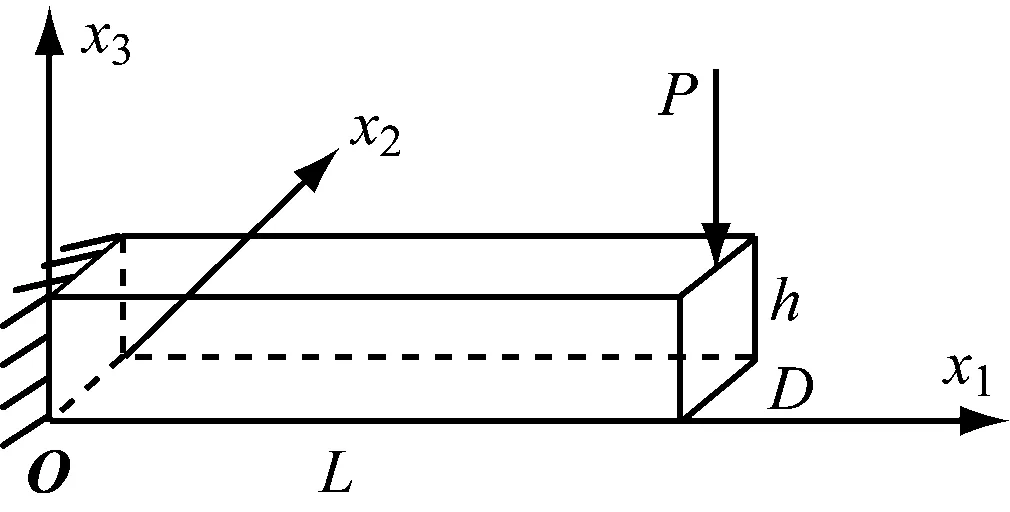
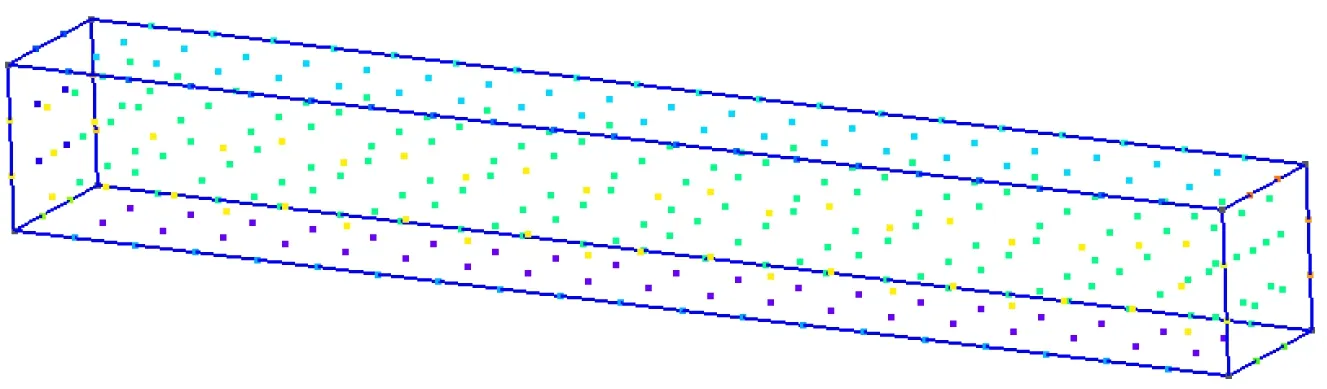
4.2 三维算例



5 结 论
