具有4个正Lyapunov指数的六维超混沌系统的复杂动力学研究

邵慧婷, 杨启贵

(华南理工大学 数学学院, 广东 广州 510640)

混沌现象广泛存在于自然现象中, 并在控制论、工程技术、密码学、经济学等领域有重要应用, 已构成非线性科学的核心研究内容。自20世纪60年代以来, 混沌理论及其应用已逐步成为非线性领域的研究热点和重点。然而如何把混沌科学发展成为一门工程技术并应用到生产生活中为人类服务，已成为21世纪非线性科学发展所面临的巨大挑战[1-2]。Lorenz系统是首个被提出的混沌系统。1963年, Lorenz[3]通过计算机数值实验发现第一个混沌吸引子，极大推动了混沌系统的发展。随着混沌研究的进一步深入, 1979年Rössler[4]提出首个四维超混沌系统, 即Rössler超混沌系统, 这是首次提出超混沌系统的概念。超混沌吸引子是指系统吸引子至少存在2个正Lyapunov指数, 其系统的动力学性质比混沌系统的混沌吸引子更加复杂, 因此超混沌系统在实际中具有更为广阔的应用前景。

众所周知，在有限维连续自治系统中, 系统的维数至少为四维且至少有1个非线性项才能产生超混沌吸引子。目前对超混沌系统的研究主要集中在四维系统和五维系统, 对六维及以上的高维超混沌系统的研究还十分少, 即使是三维混沌系统仍有许多未解决的问题。1986年, Matsumoto等[5]在研究一个结构简单的四阶电路时首次发现电路中的超混沌现象， 其他四维超混沌系统，如 Kapitaniak等[6]将2个Chua电路耦合生成超混沌系统; Li 等[7]在广义 Lorenz型系统基础上通过增加反馈控制项得到四维超混沌系统; Yang 等[8-9]在此基础上进一步研究Lorenz型超混沌系统； Hu[10]在Lorenz系统基础上通过添加线性和非线性反馈控制，得到能产生超混沌吸引子的五维系统； 张美华[11]设计了比Hu更广泛的五维超混沌系统， 这些五维超混沌系统具有比低维混沌系统更加复杂的动力学性质；Yang等[12]基于Lorenz 系统提出一类新的具有2个零特征根的高阶退化平衡点的五维超混沌系统, 并严格证明其与Yang-5D超混沌系统不等价；Yang等[13]利用耦合和控制方法首次提出一类具有4 个正Lyapunov指数的六维超混沌系统, 并研究其复杂动力学性质；Yang等[14]设计了一个新的具有5个正Lyapunov指数的新七维超混沌系统。

高维超混沌系统的研究较为复杂, 其动力学性质的证明及数值实现都十分困难, 相关研究至今仍处在起步阶段。基于经典Lorenz系统, 本文构造一类新的具有4个正Lyapunov指数的六维超混沌系统, 并研究其复杂动力学性质。运用Routh-Hurwitz准则分析该系统双曲平衡点的稳定性, 证明该系统Hopf分岔的存在性。利用计算机技术进行数值模拟, 结合相图、Lyapunov指数谱、Poincaré映射图及分岔图, 分析系统从周期、拟周期、混沌到超混沌的复杂动力学演化。

1 新六维超混沌系统

1963年, Lorenz在数值实验中发现了具有混沌吸引子的系统，即如下著名的Lorenz系统[3]。

(1)

该系统在参数(a,b,c)=(10,8/3,28)下具有混沌吸引子。基于Lorenz系统, Chen等[15]通过反馈控制技术提出一类新的混沌系统, 被称为Chen系统。

(2)

当(a,b,d)=(35,3,28)时, 可以观察到系统(2)具有与Lorenz系统不同的混沌吸引子。反馈控制技术也进一步成为研究混沌系统的重要途经之一。Lü等[16]提出一类连接Lorenz系统和Chen系统的新的3D系统, 被称为Lü系统。

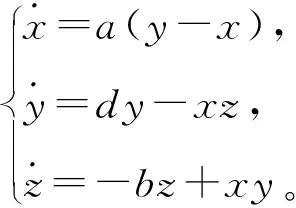
(3)

当(a,b,d)=(36,3,20),系统(3)存在混沌吸引子。

在Lorenz系统的基础上, Yang等[17]研究一类具有1个鞍点和2个稳定结焦点的三维系统, 后来被称为Yang系统。进一步, 通过在三维Yang系统上设计一个线性反馈控制器, 得到如下具有2个正Lyapunov指数的四维超混沌系统[8]。

(4)

Yang等对三维Yang系统进行进一步研究, 通过设计一个线性和非线性反馈控制, 获得如下具有3个正Lyapunov指数的五维超混沌系统系统[12]。

(5)

基于Lorenz系统和Yang-5D超混沌系统, 本文通过耦合技术和设计线性反馈控制, 提出如下一类新的六维超混沌系统。

(6)

式中{(a,b,c,e,h,k,r)∈R7|e≠0,k≠0}。

选取参数(a,b,c,e,h,k,r)=(10,8/3,28,0.1,-2,4.5,-0.9), 系统(6)存在唯一双曲不稳定平衡点O(0,0,0,0,0,0),此时系统存在1个超混沌吸引子，且具有4个正Lyapunov指数

L1=0.566 4,L2=0.297 4,L3=0.050 7,L4=0.012 2,L5=0.000 0,L6=-12.593 4。

根据系统的Lyapunov维数公式[18]

选取参数(a,b,c,e,h,k,r)=(6.1,8/3,28,40,100,10,1/28), 系统存在平衡点直线(-w/28,0,0,-61w/280,-61w/112,w),此时系统存在1个具有3个正Lyapunov指数的超混沌吸引子

L1=0.104 7,L2=0.045 0,L3=0.010 1,L4=-0.000 8,L5=-10.150 3,L6=-99.699 7。

系统的Lyapunov维数DL=4.015 7。图2分别为该组参数下系统(6)的超混沌吸引子的3维相图的投影图和Poincaré映射。

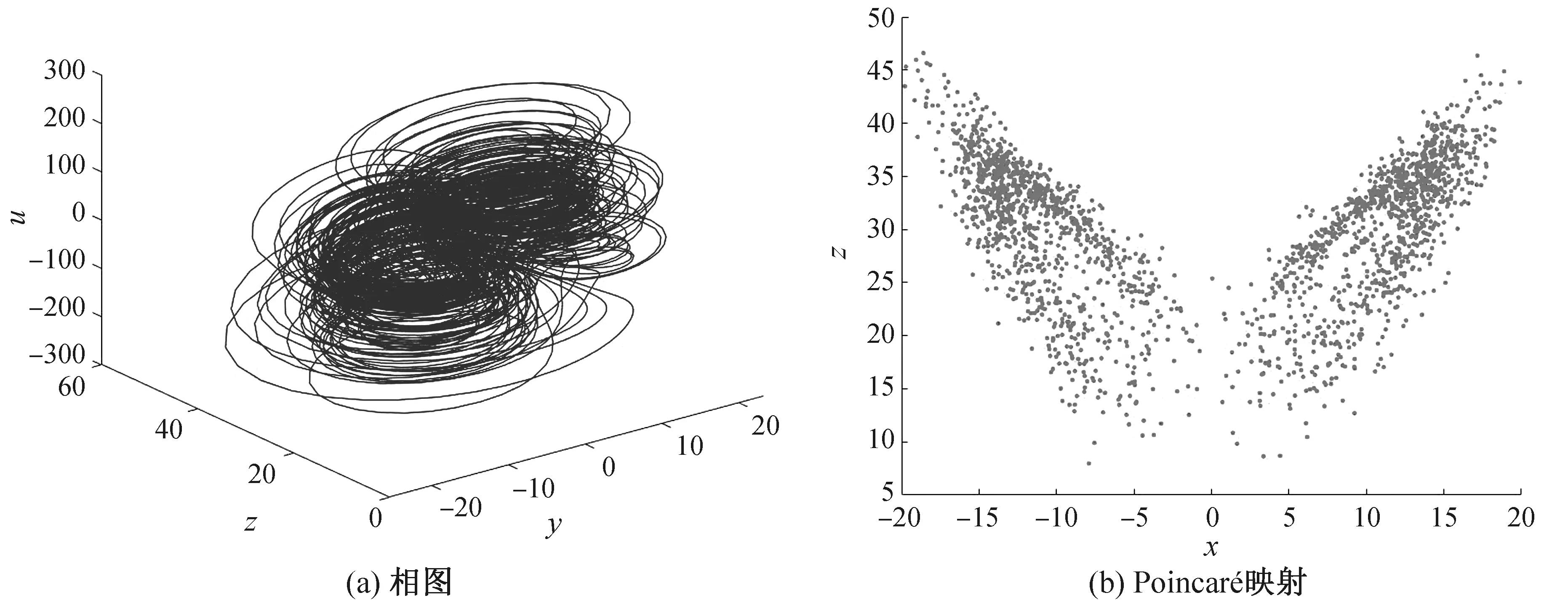
图 1 系统(6)在(a,b,c,e,h,k,r)=(10,8/3,28,0.1,-2,4.5,-0.9)下具有唯一平衡点的超混沌吸引子Fig.1 System (6) has a hyperchaotic attractor with anunique equilibrium point under (a,b,c,e,h,k,r)=(10,8/3,28,0.1,-2,4.5,-0.9)

图2 系统(6)在(a,b,c,e,h,k,r)=(6.1,8/3,28,40,100,10,1/28)下具有平衡点直线的超混沌吸引子Fig.2 System (6) has a hyperchaotic attractor with an equilibrium line under (a,b,c,e,h,k,r)=(6.1,8/3,28,40,100,10,1/28)

2 局部动力学分析

讨论系统(6)在不同参数条件下平衡点的存在情况。令

(7)

由-ky=0可得y=0, 然后将y=0代入xy-bz=0, 可得z=0。再将y=0,z=0代入cx-y-xz+w=0,-x-rw=0, 可得方程组

(8)

① 当cr≠1,ek≠0,系统(6)存在唯一平衡点O(0,0,0,0,0,0)；

下面讨论cr≠1,e≠0,k≠0时双曲平衡点O(0,0,0,0,0,0)的稳定性。

易知系统(6)的线性化系统在平衡点O处的Jacobi矩阵为

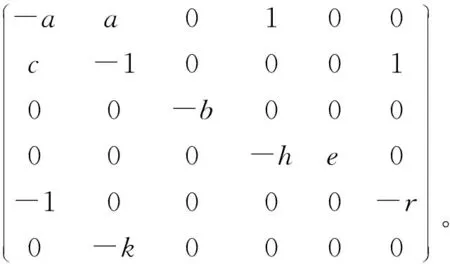
(9)

定理 1当e≠0,k≠0,cr≠1时, 系统(6)存在双曲平衡点O, 且

① 双曲平衡点O是局部渐进稳定的当且仅当(a,b,c,e,h,k,r)∈Ω,

式中：σ1=-e+h+h2+a2(1-c+h)+a(-c+(1+h)2)+k；σ2=e+ah-ach+ak+hk；σ3=1+a+h；σ4=ek-cekr；σ5=e+ahk；σ6=a-ac+h+ah+k。

② 若(a,b,c,e,h,k,r)∉Ω, 则双曲平衡点O是不稳定的。

证明系统(6)的线性化系统的Jacobi矩阵(9)在平衡点O的特征方程为

P(λ)=(λ+b)(λ5+Aλ4+Bλ3+Cλ2+Dλ+E),

(10)

式中：A=a+h+1；B=a-ac+h+ah+k；C=e+ah-ach+ak+hk；D=e+ahk；E=ek-cekr。根据定理1的条件, 其中一个特征值λ1=-b<0。令

Δ0=λ5+Aλ4+Bλ3+Cλ2+Dλ+E，

(11)

由Routh-Hurwitz定理及定理1的条件可得：

Δ1=A=a+h+1>0，

此时, 方程Δ0(λ)=0的所有根具有负实部, 从而当(a,b,c,e,h,k,r)∈Ω时, 双曲平衡点O是局部渐进稳定的; 否则O是不稳定的平衡点。证毕。

基于定理1,根据高维分岔理论,下面给出系统(6)平衡点O附近的Hopf分岔分析。

定理 2(Hopf分岔的存在性) 若系统(6)满足条件

-e-ak+(1+a)(a-ac+k)≠0,-ae+(1+a)(e-cer)+acer=0,

(1+a)(ae-2ace-2acer+2ac2er)+ce(a2+a2r-a2cr-er+cer2)=0,

(1+a)(a2ce-a2c2e+3e2+a2cer-2a2c2er+a2c3er-2ce2r)-ae2(1+c+cr-c2r)≠0,

时, 系统(6)在平衡点O处产生Hopf分岔。

证明系统(6)的线性化系统在平衡点O处的特征方程如(10)所示。设系统(6)在平衡点O处的特征方程的解有一对纯虚根λ=±iω(ω∈R+)。将λ=±iω(ω∈R+)代入式(10)可得

E-Cω2+Aω4+(Dω-Bω3+ω5)i=0。

(12)

式中：A=a+h+1；B=a-ac+h+ah+k；C=e+ah-ach+ak+hk；D=e+ahk；E=ek-cekr。因此,

E-Cω2+Aω4=0，Dω-Bω3+ω5=0。

(13)

由定理条件

(1+a)(ae-2ace-2acer+2ac2er)+ce(a2+a2r-a2cr-er+cer2)=0,

(1+a)(a2ce-a2c2e+3e2+a2cer-2a2c2er+a2c3er-2ce2r)-ae2(1+c+cr-c2r)≠0,

-ae+(1+a)(e-cer)+acer=0,

可得

从上述分析可得λ1=-b<0,λ2=iω0,λ3=-iω0,根据定理2条件,

特征方程的其余3个特征根满足

由Routh-Hurwitz定理可得，若

则系统(6)在平衡点O处的其余3个特征根均有负实部, 满足Hopf分岔的第一个条件[19-21]。

由式(11)可得

满足Hopf存在的第2个条件[19-21]。因此, 系统(6)在平衡点O处存在Hopf分岔。证毕。

3 数值复杂动力学分析

利用数值模拟方法对系统(6)在某些参数下的性质进行分析, 获得系统的复杂动力学。选取系统参数(a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9)固定不变, 改变参数h∈[-2.5,3]时,系统出现从超混沌、混沌、拟周期、周期、拟周期到超混沌的复杂动力学变化, 并且分别存在具有4个、3个、2个正Lyapunov指数的超混沌吸引子。图3为h∈[-2.5,3]时, 系统(6)的Lyapunov指数谱; 表1为h取某些特殊值时其对应的动力学现象。图4为h∈[-2.5,3]时, 系统(6)的分岔图; 图5为典型的h参数值下系统的吸引子相图。图5刻画了系统(6)从超混沌吸引子退化到周期轨又演化到超混沌吸引子的过程。

选取系统参数(b,c,e,h,k,r)=(8/3,28,40,100,10,1/28)固定不变, 根据第2章关于系统平衡点的分布的分析可知, 系统(6)存在平衡点直线。改变参数a∈[0.1,10],系统出现从周期、拟周期、混沌到超混沌的复杂动力学变化, 并且分别存在具有2个、3个正Lyapunov 指数的超混沌吸引子。图6为a∈[0.1,10]时,系统(6)的Lyapunov 指数谱; 表2为a取某些特殊值时其对应的动力学现象。图7为a∈[0.1,10]时, 系统(6)的分岔图; 图8为典型a参数值下系统的吸引子相图。从图7所示的系统分岔图可知, 当a∈[0.1,3]时, 系统发生倍周期分岔进而演化成超混沌吸引子。

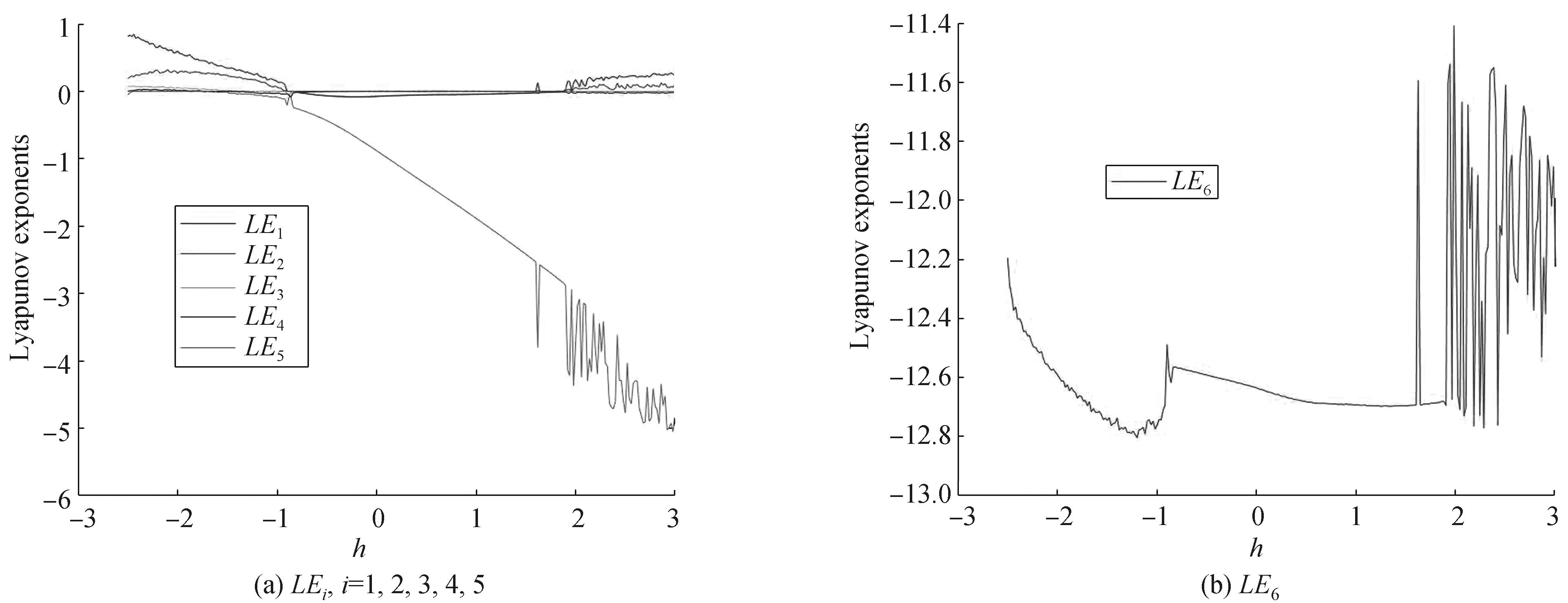
图3 系统(6)的Lyapunov指数： (a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9), h∈[-2.5,3]Fig.3 Lyapunov exponent graph of system (6): (a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9), h∈[-2.5,3]

图4 系统(6)的分岔：(a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9), h∈[-2.5,3]Fig.4 Bifurcation diagram of system (6): (a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9), h∈[-2.5,3]

表 1 系统(6)在参数(a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9)下的动力学行为

图5 系统(6)在(a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9)的相图Fig.5 Phase diagram of system (6) with parameters (a,b,c,e,k,r)=(10,8/3,28,0.1,4.5,-0.9)

图6 系统(6)的Lyapunov指数：(b,c,e,h,k,r)=(8/3,28,40,100,10,1/28), a∈[0.1,10]Fig.6 Lyapunov exponent graph of system (6): (b,c,e,h,k,r)=(8/3,28,40,100,10,1/28), a∈[0.1,10]

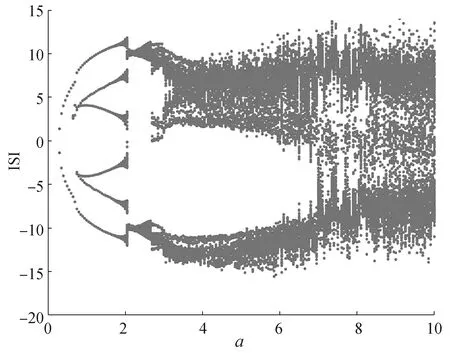
图7 系统(6)的分岔图：(b,c,e,h,k,r)=(8/3,28,40,100,10,1/28), a∈[0.1,10]Fig.7 Bifurcation diagram of system (6): (b,c,e,h,k,r)=(8/3,28,40,100,10,1/28), a∈[0.1,10]

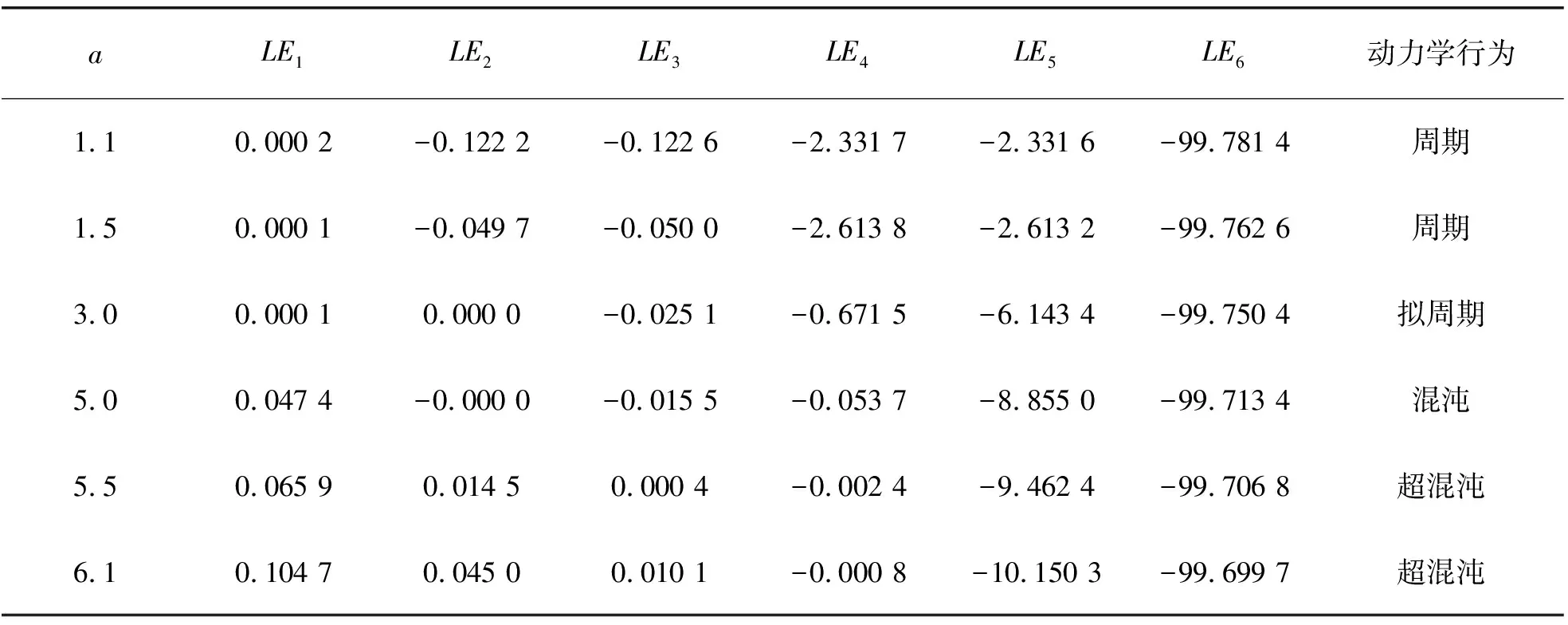
表2 系统(6)在参数(b,c,e,h,k,r)=(8/3,28,40,100,10,1/28)下的动力学行为

图8 系统(6)在(b,c,e,h,k,r)=(8/3,28,40,100,10,1/28)的相图Fig.8 Phase diagram of system (6) with parameters (b,c,e,h,k,r)=(8/3,28,40,100,10,1/28)

4 结语

本文以Lorenz系统为基础, 运用耦合方法并设计线性反馈控制, 发现1个新的在仅有1个双曲平衡点的情况下具有4个正Lyapunov指数，且在具有平衡点直线的情况下具有3个正Lyapunov指数的六维超混沌系统。运用Routh-Hurwitz准则分析该系统双曲平衡点的稳定性, 利用高维分岔理论证明该系统Hopf分岔的存在性。通过数值模拟, 分析该系统的复杂动力学性质, 有机融合相图、Lyapunov 指数谱、Poincaré映射图及分岔图, 分析系统从周期、拟周期、混沌到超混沌的复杂动力学变化, 数值验证了新六维系统通过倍周期分岔产生超混沌吸引子的途径。对该新六维超混沌系统的动力学分析表明：该系统具有复杂的超混沌、分岔等动力学性质, 可在密码学、控制论等实际应用领域提供一定的潜在应用前景。