可压缩非守恒两相流模型

张映辉, 叶 琴

(广西师范大学 数学与统计学院, 广西 桂林 541006)

众所周知, 自然界中大部分流体都是多相流。多相流包括不相容混合流, 如空气和水混合流, 油、气和水混合流。当2种流体相容时, 它们通常形成一种新的具有自身流变特性的单一流体。如稳定的水油乳状液是非牛顿流体, 但水和油本身都是牛顿流体。最简单的非平凡多相流是在空气和水之间的界面上传播的小振幅波, 空气和水的运动规律由一对具有自由界面的可压缩 Euler 方程组刻画:

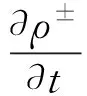
(1)

(2)

式中：ρ+、u+、P+分别表示水的密度、速度和压强；ρ-、u-、P-分别为空气的密度、速度和压强；g为重力；拖曳力FD满足

C、为给定的物理参数。

水和空气被未知的自由界面z=η(x,y,t) 分开, 该自由界面满足如下动力学方程

式中, 压力连续地穿过该自由界面, 即P+=P-=P。

当波的振幅足够大时, 可能出现波爆破。在空气和水之间界面的周围区域,气体中出现小液滴,液体中也出现气泡。由于坍塌和破碎的出现,自由界面的拓扑结构变得相当复杂,并涉及到各种不同的尺度。简化多相流的复杂性并且满足工程师需求的经典方法是体积平均法,可参看文献[1]了解其更多物理背景和应用。用α+、α-分别表示水和空气的体积分数并作用于式(1)、(2),通过体积平均方法可推导出一个没有自由界面的模型——两相流模型

(3)

两相流模型不仅用于刻画水和空气之间的分离流, 还广泛应用于电力、核能、化学工艺、油气、低温空间、生物医学、微技术等, 参看文献[2-8]和其引用文献了解更多物理背景和应用。用于模拟不同实际背景的模型具有差异, 但是平均模型与系统(3)具有相同的结构。

下面用流体+和流体-分别表示2种非混溶流体, 如上述的水可用流体 + 表示,空气可用流体-表示,引入黏性力和毛细管效应,将模型(3)推广为如下可压缩非守恒两相流模型

(4)

式中：α+、α-分别表示流体+和流体-的体积分数,α±∈[0,1]；ρ±、u±、P±分别表示流体+和流体-的密度、速度、压强；应力张量τ满足

(5)

常数μ±、λ±为2种流体的剪切黏性系数和膨胀黏性系数;毛细管效应参数σ±>0。模型(4)及其相关模型的适定性、大时间行为、渐近性等内容可参看文献[4,8-28]和其引用文献。

可压缩非守恒两相流模型(4)具有非守恒性和强耦合性, 至今研究成果还很少。下面按流体压强相等且有毛细管效应(P+=P-=P,σ±>0)、压强不相等且无毛细管效应 (P+≠P-,σ±>0)、压强相等且无毛细管效应(P+=P-,σ±=0)这3种情况分别讨论该模型的研究进展。

1 压强相等且有毛细管效应

1.1 模型

设2种流体压强相等, 并且有毛细管效应。于是式(4)可改写为

(6)

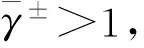
μ±(ρ±)=v±ρ±,λ±(ρ±)=0,

v±为给定的常数。文献[31]中,剪切黏性系数μ和膨胀黏性系数λ满足

μ±>0,λ±+2u±>0。

2种流体的声速s±满足

则有

(7)

令R±=α±ρ±,则

(8)

(9)

将式(9)代入式(8), 得

(10)

结合式(7), 有

(11)

于是,式(6)可改写为

(12)

式(12)的初值条件如下

(13)

其中

(14)

(15)

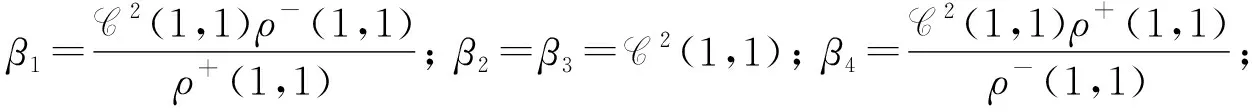
F1=-div(n+u+)；

(16)

F3=-div(n-u-)；

(17)

式(16)、(17)中,

式(15)的初值条件为

式中

(n+,u+,n-,u-)(x,t)→0,|x|→∞。

1.2 模型(6)研究成果

并且

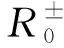
则周期域问题(12)～(14)在[0,T]上存在全局弱解(α±,ρ±,u±)。

定理2(三维柯西问题小初值光滑解的全局存在性和衰减率)[30]若对任意整数s≥3,存在常数δ>0,使得

则柯西问题(12)～(14)在[0,∞]上存在全局强解(ρ±,α±,u±),满足

R+-1,R--1∈C0([0,∞];Hs+1(R3)∩C1[0,∞];Hs(R3)),

u+,u-∈C0([0,∞];Hs(R3)∩C1[0,∞];Hs-1(R3)),

且存在与t无关的c>0,C>0使得

解满足如下衰减估计

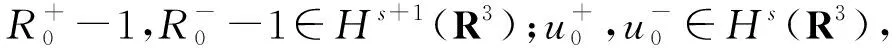
则柯西问题(12)～(14)存在全局强解 (R+,u+,R-,u-) 满足

R+-1,R--1∈C0([0,∞];Hs+1(R3)∩C1[0,∞];Hs(R3)),

u+,u-∈C0([0,∞];Hs(R3)∩C1[0,∞];Hs-2(R3)),

且

衰减率上界估计：对任意t≥0,0≤k≤s,有

其中ϑ<2,s>2为给定的常数,则存在与t无关的常数k,且0≤k≤s,对任意足够大的t,有

注1定理1考虑特殊的黏性情形为μ±(ρ±)=μ±ρ±,λ±(ρ±)=0,利用紧性建立了三维周期域问题全局弱解的存在性。然而,文献[29]中的方法很大程度上依赖于毛细管效应和特殊的黏性,不能处理无毛细管效应(σ±=0)和常黏性系数情形。定理2考虑更特殊的黏性和相等的毛细管系数为μ±(ρ±)=νρ±,λ±(ρ±)=0,σ+=σ-=σ>0,证明三维柯西问题小初值光滑解的全局存在性和衰减率。文献[30]的主要方法是基于特殊的黏性和相等的毛细管系数,将模型(6)分解为2个4×4系统,它们的线性部分与可压缩Navier-Stokes-Korteweg方程的线性部分拥有类似的耗散结构。但是文献[30]中的方法不适用于常黏性系数和不相等的毛细管系数情形。定理3考虑具有常黏性系数和不相等的毛细管系数(μ±(ρ±)=μ±>0,λ±(ρ±)=λ±,σ+≠σ->0),证明三维柯西问题小初值光滑解的全局存在性和最优衰减率。文献[31]通过引入比例密度的线性组合以及2个新的时间加权能量泛函, 利用巧妙的矩阵分解、精细的谱分析和两系能量方法证明了该结论。

2 压强不相等且无毛细管效应

2.1 模型

设2种流体压强不相等, 且无毛细管效应。 于是式(4)可改写为

(18)

其中应力张力τ满足式(5),剪切黏性系数μ±>0,膨胀黏性系数λ满足λ±+2μ±>0,f(α-ρ-) ∈C3([0,∞]),且在平衡态附近f(α-ρ-) 为严格减函数，式(9)～(11)可改写为

令

则在(R+,+∞)中

由于P+(ρ+)-P-(ρ-)=f(α-ρ-),故存在ρ+=ρ+(R+,R-),使得φ(ρ+)=0。令

则式(18)可改写为

(19)

式(19)的初值条件为

(20)

式中

(21)

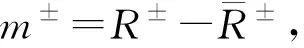
(22)

其中

(23)

(24)

式(22)右端

G1=-m+divu+,G2=-m-divu-,

(25)

(26)

1≤i,j≤3。式(25)～(26)中

式(22)的初值条件如下

式中

(n+,u+,n-,u-)(x,t)→0,|x|→∞。

2.2 模型(18)研究成果

定理 4(三维柯西问题光滑小解的全局存在性和衰减率)[18]若存在适当小的固定常数η>0,使得

(27)

且存在常数ε,使得初值满足

则柯西问题(19)～(21)存在全局强解(R+,u+,R-,u-)满足

R+-1,R--1∈C0([0,∞];H2(R3)∩C1([0,∞];H1(R3)),

u+,u-∈C0([0,∞];H2(R3)∩C1([0,∞];L2(R3)),

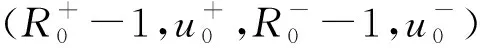
注 2证明定理4,通常需对相应线性化系统进行格林函数的谱分析和对非线性系统做能量估计。文献[18]中,只需要对格林函数的低频部分进行谱分析和能量估计,可以在频率空间中使用能量估计的方法得到低频部分的衰减率,从而避免对格林函数的复杂分析,并且可以直接通过能量估计处理高频部分。即使初值在H2框架中,解的衰减率也可以通过低频部分的衰减率和能量估计得到。

则柯西问题(19)～(21)存在全局强解(R+-1,u+,R--1,u-)满足

R+-1,R--1∈C0([0,∞];HN(R3)∩C1[0,∞];HN-1(R3)),

u+,u-∈C0([0,∞];HN(R3)∩C1[0,∞];HN-2(R3))。

衰减率下界估计：设β1、β4满足式(24)、(25),令

则存在与t无关的常数C0>0，当t足够大时，

定理 6(三维初边值问题全局小解的存在性和指数稳定性)[21]Ω是一个光滑的有界域,且Ω⊆R3，∂Ω∈C4，边界条件为

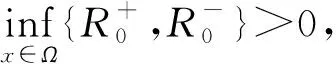
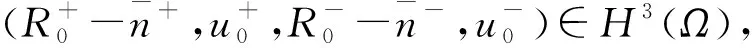
则初边值问题(19)～(20)存在全局强解(R+,u+,R-,u-),并且,若

则全局强解(R+,u+,R-,u-)满足

此外,存在与t无关的常数θ>0,使得

注 3定理4假定f在平衡态附近严格递减,得到了三维柯西问题光滑H2小解的全局存在性和衰减率。文献[18]指出这一假定在整个证明过程中起到至关重要的作用,对该模型具有本质的稳定性效应,但是文献[18]的方法不能处理压强相等(f≡0)的情形。定理5假定初始扰动的H2范数充分小但其高阶空间导数可以任意大,证明了三维柯西问题的解及其各阶空间导数的最优上界和下界衰减率。文献[32]通过Hodge分解技巧、高-低频分解和时间加权能量估计，将文献[18]的结果推广到一般的HN(N≥2)情形。定理6得到三维初边值问题全局小解的存在性和指数稳定性。

3 压强相等且无毛细管效应

3.1 模型

设2种流体压强相等,且无毛细管效应。于是式(4)可改写为

(28)

在一维域Ω=(0,1)上,模型(28)可改写为

(29)

不失一般性,设μ±=1,假设ρ>0,令R±=α±ρ±,于是式(29)可改写为

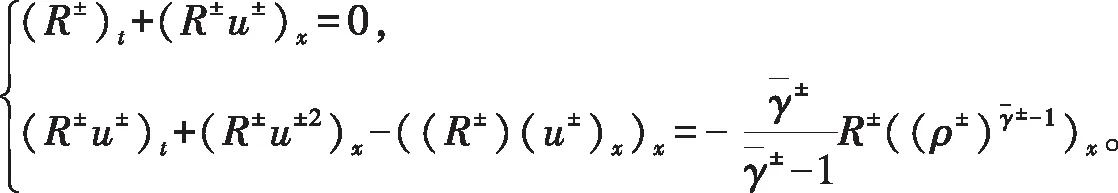
(30)

式(30)的初值条件为

(31)

式(30)的边界条件为R±u±|x=0=R±u±|x=1=0。

3.2 模型(28)研究成果

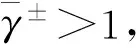
注4文献[33]得到定理7的方法强烈依赖于一维空间的优势,并不适用于高维问题。由于模型(28)相应的线性系统有零特征根,比例密度(α±ρ±)没有任何耗散,并且该模型是非守恒系统，且具有强非线性性,这些给该模型的数学分析(适定性和稳定性)带来很多本质上的困难。至今,系统(28)的高维问题没有任何数学结果,这将是今后工作的重点。

4 结语

本文分别介绍2种流体压强相等且有毛细管效应、2种流体压强不相等且无毛细管效应、2种流体压强相等且无毛细管效应3类可压缩非守恒两相流模型及其研究成果，其中,2种流体压强相等且无毛细管效应的高维可压缩非守恒两相流模型的线性系统含零特征根,这使得该问题的数学分析变得十分复杂和困难,该模型至今无任何数学成果,这将是今后研究的重点。