几何形态测量学及其在直翅目研究中的应用

陆相宜, 边 迅 *, 邓维安

(1.珍稀濒危动植物生态与环境保护教育部重点实验室(广西师范大学), 广西 桂林 541006；2.广西珍稀濒危动物生态学重点实验室(广西师范大学), 广西 桂林 541006)

不同生物有不同的形态结构，同一生物在不同生长阶段或不同性别之间的形态特点也存在一定差异，因而形态学在生物系统学中有着重要地位。形态学最初阶段是通过肉眼直接比较，对间断性形态差异进行描述，从而获得定性的结果[1]。形态测量学是基于形态学发展而来的一个分支，主要对生物形状和形状变化进行定量描述、分析和解释。传统的形态测量方法建立在一些点对点测量(距离、比率或角度)的统计分析基础之上，反映被研究生物的形态特征[2]，其最常用的数据变量为线性距离(linear distance)，主要是生物体中任意两点之间的直线距离，或能用直线距离表示的特征(例如角度、面积、体积等)。虽然传统形态测量学发展到后期将多元统计与形态性状的数值表征相结合，但线性距离作为形态学研究中的单变量难以真正捕获并保存样本的空间形态信息。20世纪80年代，学者突破传统形态测量学的局限，开始着重比较生物体的拓扑结构，通过标志点和标志点相对位置几何信息的匹配，利用标志点坐标的空间相对位置几何信息反映生物体的几何形状[3]，几何形态测量学逐渐得以发展；20世纪90年代，研究人员针对生物外形差异，基于笛卡尔坐标使用几何形态测量法(geometric morphometrics)捕获生物的形状，并通过多元统计方法储存分析这些形态特征信息，被称为“几何形态测量学的革命”[4-5]。几何形态测量学使得生物体的形态特征能通过数据体现出来，并用于生物分类和系统发育分析。

几何形态测量学在一定程度上解决了形态分类的不确定性，并可以区分隐存种，是根据表型鉴定不同类群的有力工具，已广泛应用于多个领域[6-12]。昆虫外骨骼和翅易测量，不像其他动物的软体组织会发生物理形变。Daly[13]首次将几何形态测量学应用于昆虫研究。此后，几何形态测量学在昆虫领域的应用才逐渐成熟。国内几何形态测量学起步较晚，自白明等[1]系统阐述几何形态测量学原理及应用之后才陆续有相关研究开展。在几何形态测量法的应用中，学者对其数据分析方法和应用软件多有报道，其中Baltanás等[2]的几何形态测量学常用方法和软件较为全面。随着几何形态测量学日臻成熟和完善，新的几何形态测量学方法和软件不断提出[14-18]。本文对几何形态测量学常用分析方法和软件进行整理，同时介绍几何形态测量学在直翅目研究中的应用现状，以期为直翅目昆虫研究提供新思路。

1 几何形态测量学

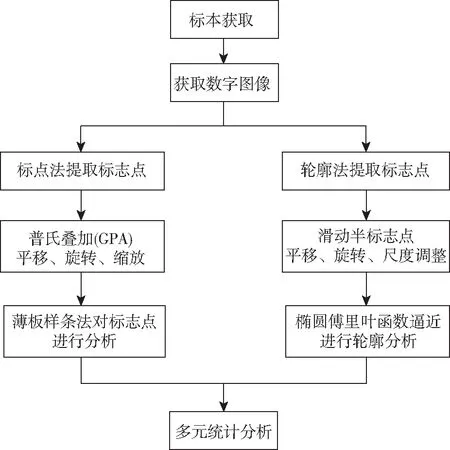
图1 几何形态测量学分析流程(改编自杨红珍等[20])Fig.1 Geometrical morphometry analysis process (Modified from Yang, et al[20])

几何形态测量学方法注重比较生物体自身形状，选取笛卡尔坐标数据(cartesian coordinates)后通过缩放、旋转、重叠等方式分离坐标中形态因素与非形态因素[19]。几何形态测量学的分析流程[20]如图1所示。

1.1 标点法与轮廓线法

标点法(landmark methods)与轮廓线法(outline methods)是几何形态测量学重要的方法，都是建立在将界标点(landmark)作为数据变量的基础上。标点法数据类型为界标点与半界标点，而轮廓线法数据类型主要为曲线函数。Bookstein[21]确定了3种界标点类型：第1类(I型)为组织或结构之间的交点；第2类(II型)为形态曲线切点，即曲线拐点；第3类(III型)为能够涵盖组织或结构最大位置信息的边缘点。第1种类型的界标点倾向于描述生物的几何形状，第2种和第3种构成了大量的线性距离，能更准确描述研究对象的形状[22]。

界标点法取点的准确性很大程度上影响着应用效果。因此在取点过程中要合理选取界标点并剔除无效界标点，在降低点与点之间联系的同时尽可能涵盖形态特征信息[23]。界标点的选取标准见表1[24]。通常根据研究对象及实验目的的不同，界标点的类型和位置选取不同，见表2。

轮廓线(outline)指生物组织或结构的轮廓曲线。与线性距离相比，选取轮廓线更能完整准确反映生物体的轮廓形态。轮廓线常转化为一系列半界标点，或界标点与半界标点组合。学者通常使用Edgewarp法[25-26]和垂直投影标准[27]使界标点沿着曲线对齐。Sheets等[27]在三叶虫个体发育轮廓形态变化研究中，列举了2种半界标点法(Edgewarp法和垂直投影标准)，并与界标点法进行比较，结果显示，半界标点能更准确表示个体的形状变化信息。因此，对于一段曲线或复杂轮廓的描述，运用半界标点表示轮廓比界标点更加准确。

标点法的优点在于数据选取清晰容易、数据量少、计算量小[28]，但也存在不足：一是，由于选取点的不连贯性，许多细微的形状变化易被忽视；二是，标点法同源点选取是否正确，也在一定程度上影响数据分析结果与性状特征的描述[29]。反之，轮廓法可以完整反映轮廓形态变化，却不能分析更复杂的内部形态结构。由于标点法与轮廓法优缺点的互补性，两者结合更能满足实验要求。例如，Dalayap等[30]将轮廓法

表1 界标点选取通用标准[24]

表2 不同类群选取界标点的位置和类型

与标点法相结合对莫氏兰科的花瓣、萼片及唇瓣进行形态定量描述和分析，2种方法相互补充，能将数据测量误差最小化，更准确地描述了4个品种花瓣、萼片及唇瓣的形状变化，促进了对生物性状分化的理解，有助于基于花瓣、萼片和唇瓣等特征的分类和辨别。

1.2 薄板样条分析和傅里叶分析

薄板样条分析(thin-plate spline)是标点法主要的分析方法之一，而傅里叶分析(fourier analysis)是轮廓线主要的分析方法。

薄板样条分析在离散的界标点之间进行插值，将原本的网络坐标轴系统转换成扭曲变化的坐标轴函数，通过扭曲能量矩阵呈现出变形网格及其变量的问题，从而直观看出形态的差异或变化。Swiderski[40]用薄板样条分析描述了树松鼠(tree squirrels)、花栗鼠(chipmunks)和地松鼠(ground squirrels)肩胛骨之间的形状差异，揭示肩胛骨的演变过程，说明了薄板样条分析在形态转换研究中的实用性。薄板样条分析法运用特征分析(eigen analysis)及主成分分析等统计方法，将主要扭曲(principal warp)、部分扭曲(partial warp)、相对扭曲(relative warp)等变量，通过一系列复杂运算，用数学方法描述研究对象的形状变化，并将差异以变形网格的方式表示出来[28]。

傅里叶分析法属于谐波分析，其因未能考虑同源性而受到批评，但当无法识别一组同源点时，此类方法非常有用[41]。傅里叶分析法有：径向傅里叶分析(radial fourier analysis)、Z-R傅里叶分析(Z-R shape function)和椭圆傅里叶分析(elliptical fourier analysis, EFA)，其中椭圆傅里叶分析法是迄今为止在动植物分类及系统发育研究方面运用最为有效和广泛的一类轮廓法[29]，其以一系列曲线来表示形状轮廓。与界标点法相比，轮廓分析法无需定量分析生物形状的总轮廓，而是将同源点或形状简化为一系列曲线[42]。因此，椭圆傅里叶分析特别适合分析没有明显变化的形态学特征的生物或形状集[43]。Emmons等[44]用椭圆傅里叶分析辨别东太平洋3种生态型的虎鲸背鳍、背上斑块和眼斑块的形状差异，表明表型分化形成与其栖息地、行为、饮食等的差异相关，并将椭圆傅里叶分析法应用到鲸类的形态计量学研究中。

1.3 主成分分析和系统发育主成分分析

主成分分析(principal components analysis，PCA)是几何形态测量学的一个重要步骤，能反映生物形态变化，可作为形态变量数字化并用于后续分析的工具[21,45]。主成分分析作为几何形态测量学常用的降维方法，它从所有变量中删除冗余或与之密切相关的变量，建立彼此不相关的新变量，同时基于原有信息将新变量数目最小化。根据主要成分的得分绘制样本散布点图，得出各种样本的分布可能是离散、重叠或交错的。姜晓东等[46]基于地标点研究不同水系野生中华绒螯蟹，根据2个主成分绘制散点图，结果显示各群体之间虽有部分重叠, 但大体形成较为集中的区域，可区分出不同水系的野生中华绒螯蟹。也可以通过计算各主成分的贡献率，并选出贡献率高的主成分作为主要分类依据，进而鉴别相似物种，例如车星锦等[47]以澜沧江水系196 尾荷马条鳅属Homatula鱼类标本为研究对象，通过主成分分析找到能够区分尾荷马条鳅不同类群的主要鉴别特征，同时发现了该属3个新种。尽管目前主成分分析的应用相当广泛，但Uyeda等[48]认为，主成分分析采用多元分析的偏置取样，专注于前几个主成分的分析，因此反映的结果会有偏差，造成统计假象。

在进行数据分析时，忽略系统发育可能会导致分析结果产生更大的误差[49]。近年来，考虑系统发育和物种间非独立性的多元数据排序的系统发育主成分分析(phylogenetic principal components analysis，pPCA)被提出[50]。与传统的主成分分析不同，系统发育主成分分析的得分是相互关联的。系统发育主成分以形状变异的非系统发育为导向，但得分在空间位置上保留系统发育协方差，使图中显示的视觉信息成为非系统发育和系统发育的杂合[50]。Baab等[51]分别使用主成分分析和系统发育主成分分析研究饮食和活动方式对马达加斯加狐猴进化的作用，发现在不考虑系统发育时，饮食和活动方式都影响了其进化；而当考虑系统发育时，只有饮食对其产生影响。但系统发育主成分分析方法可能会使得分析结果偏向某一特定进化模式，而不能反映性状多样化的过程[49]。

1.4 聚类分析

聚类分析(cluster analysis)是在欧氏距离基础上对研究对象的所有性状差异进行度量，其可根据距离判断各种群之间的亲疏关系从而进行分类。聚类分析方法综合多种因素对未知类群、相似类群进行划分，拓宽了几何形态测量学在各研究领域的应用。近年提出的加权主成分聚类分析方法集成了传统聚类分析、加权聚类分析、一般主成分聚类分析等的优点，能避免因指标之间高度相关性的影响或过度强调某一主成分的重要性而使聚类结果失真[52]。聚类分析方法的优化能有效解决科学研究过程面临的难题，为学者提供极大便利。Wang 等[53]基于地标的几何形态测量学对2种树蜂科Siricidae昆虫Sirexnoctilio和S.nitobei的翅、触角和产卵器形态进行量化和分析，结果表明，通过翅和产卵器的聚类分析能准确区分2个物种。

1.5 判别分析

判别分析(discirmiant analysis)是一种根据已知样本的观测数据确定判别函数，根据现有的判别标准比较分类未知样本的分析方法[54]。主要的判别分析方法有Fisher判别法、距离判别法、Bayes判别法和最大似然判别法等。判别分析中常用判别空间的度量是马氏距离，而马氏距离已成为区分物种、亚种甚至地理或生态种群等形态变化的最有效方法之一[55]。

Fisher判别法在Fisher准则函数最大化的情况下将样品空间维数投影到Fisher最佳判别向量，从而减小计算的维数空间，能解决差异不明显的各类数据，从而达到判别效果。刘昌景等[56]以鸮形目Strigiformes的6种鸟类飞羽羽长、阳面羽枝长、阴面羽枝长、羽毛面积、深色羽斑面积进行Fisher判别分析，结果表明5个量化指标能准确鉴定出各物种，说明Fisher判别分析可进行种属分类鉴定。

距离判别法是根据观测样本的若干数量特征对新获得的样本进行归类、识别，判别其所属类型的一种统计分析方法[57]。起初，距离判别中的距离是指马氏距离，主要进行线性判别分析，但对于复杂的球形数据判别效果不佳。黄利文[57]提出基于欧氏距离的判别分析，并通过实例表明该方法在处理球形数据判别问题时明显提高了判别效果。唐宇政[58]比较了2种判别分析方法，并基于花瓣长度和花瓣宽度利用欧氏距离判别法对鸢尾花进行分类，结果表明基于欧氏距离的区分度更高，判别效果良好。基于马氏距离和基于欧氏距离的距离判别法相互补充，扩大了距离判别分析方法的应用广度和深度。然而距离判别没有考虑个体出现机会的大小，也没有考虑错判带来的损失[59]，因此可能产生较大的误差。Bayes判别法将平均误判损失最小化，从而提高了判别准确率。肖培等[60]通过Bayes判别法鉴定9种布氏杆菌常见种，并用回代法和刀切法将样本数据回代评价模型判别效果时，发现除了牛种、羊种和猪种出现错判外，其余均判断无误，总体判断准确率高，说明Bayes判别模型具有较高的灵敏性和稳定性。

最大似然判别法根据先前建立的判别函数集来计算各分类样品的归属概率，进而分类[61]。Sumruayphol等[62]应用距离判别法、最大似然判别法、人工神经网络法对比辨别不同种类肝片吸虫，结果表明距离判别法的精度虽然较高，但是其基于的假设有时与形态学数据不符合，而最大似然判别法和人工神经网络法分析效果更好。

1.6 模块集成分析

形态模块性(modularity)是指生物体在结构或功能上划分为小的单元模块，这些模块在局部发育过程互相分离，在变异、进化中相对独立。因此模块化的发展被认为是促进了形态多样化的发生。集成(integration)是指生物体功能和发育相关性状的协调变异。研究集成的基础是探究不同自然种群之间在形态测量学上的协方差或相关性[63]。集成强度可以通过变异在表现型空间维度的分布体现出来。若变异集中在同一维度，集成强度最大，表明所有形态测量值都相关；若变异在多个维度上分布，则不存在集成。目前，基于形态学数据，模块性集成已在发育、基因、功能、进化等各种生物背景下都有研究，几何形态模块集成分析主要用于探究生物体中多个器官是以一个整体结构进化，还是分为几个不同模块分别进化。此分析在数据获取时常运用标点法，利用聚类分析判断不同器官是模块进化还是整合进化。Goswami[64]运用聚类分析将1 832个哺乳动物三维颅面分为6个不同的模块开展实验，发现所有标本中只有3个模块显著集成。MINT软件可精确判断模块可接受性[65]。Larouche等[66]用MINT软件对Daniorerio和Chrosomuseos这2个种的地标协方差矩阵进行拟合，最佳拟合模型显示头部没有整合，尾鳍、背鳍、臀鳍作为一个模块，而成对的胸鳍和腹鳍各自内部产生了不同的整合模式。理解形态整合和模块性之间的相互作用是研究复杂结构形态演化的一个重要内容[67]。Monteiro等[68]探究了叶口蝠科Phyllostomatidae下颌骨的进化整合关系，认为进化整合过程在一定程度上是生物体器官自然选择的结果，与模块发育无必然关系。

几何形态测量学作为低成本研究方法推动着各学科的发展，受到不少学者青睐。通常几何形态测量学运用多种方法(例如椭圆傅里叶分析、主成分分析和聚类分析结合[69]或主成分分析法、典型变量分析法、薄板样条及聚类分析结合[70]等)进行综合分析，以提高研究结果的可靠性。

2 几何形态测量学常用软件

随着数学与统计学不断发展，形态测量学在生物学中的研究范围也随之扩展，用于数据获取、统计分析、可视化图像生成等的软件工具衍生而出。本文统计了常见的应用软件，见表3。

表3 常用几何形态测量学应用软件

传统的形态测量学分析方法往往需要分析运算大量坐标数据，需由多个软件完成，过程耗时且繁琐。迄今为止，越来越多学者致力于将界标点数据分析与现代化大数据分析相结合，通过数据集成分析快速、方便地得出界标点数据分析结果。例如，Geomorph综合性软件可以实现在同一软件中完成多种分析[17]。白明等[18]开发的web数据工具，可对多个特征信息进行组合比较，并能从特定类群或研究对象的多个特征中得出整体相似度估值。

3 几何形态测量学在直翅目中的应用

几何形态测量学大多致力于脊椎动物研究上，在昆虫领域，国内昆虫几何形态学研究主要集中在鳞翅目、鞘翅目、膜翅目、长翅目、蜻蜓目及脉翅目[85]。直翅目中几何形态测量学的研究报道相对较少，且主要集中在分类鉴定和形态变异方面。

3.1 几何形态测量学在直翅目分类研究中的应用

直翅目主要依据前胸背板、翅型和翅脉脉序、生殖器、足等外部形态特征描述进行鉴定。这种方法虽能直观表示生物的形态结构，但是要求鉴定者具有较高的专业水平，且将定性的形态信息量化为能直接进行统计分析的数据。几何形态测量学是一个可保留细微信息且可将形态信息数字化的高效、准确方法，为生物分类提供了可靠的分析途径。例如，邓维安等[32]对20种蚱类昆虫前胸背板特征进行因子分析、主成分分析和聚类分析，主成分分析得出蚱类昆虫科级水平上常用的分类特征是可靠的，聚类分析则将20种蚱准确分为4大类群。温光华等[86]借助几何形态测量法对稻蝗属Oxya5个常见种的雄性前、后翅形态变化进行分析，揭示了5种稻蝗分类关系。Zhang等[87]利用形态测量学方法分析蚱类昆虫后翅脉序的形态特征，结果表明，不同属的后翅脉序存在较大差异，因此脉序的形态特征可作为分类鉴别依据。Rebrina等[88]研究发现，通过体长和前胸背板长不能准确区分Paramogoplistesnovaki和Mogoplistesbrunneus，但通过下生殖板的形状差异却能正确鉴别这2个种。Liu等[89]以螽斯亚科盾螽属Decticus为研究对象，结合翅、外生殖器的几何形态测量学分析和声学信息分析，鉴定出我国盾螽属至少有5种(亚种)。

3.2 几何形态测量学在直翅目生态适应与形态变异研究中的应用

几何形态测量学被用来探讨种下、种间的形态差异和变异部位，揭示特定结构之间或结构与环境因子等之间的进化相关性。Oneal等[90]研究Amphiacustasanctaecrucis7种不同生境中种群个体下颚和雄性生殖器官的差异，探讨生态选择和性别选择是否是导致种群分化的主要原因，多元方差分析和典型变量分析结果表明，物种产生分化主要是由生态环境不同引起的。Bai等[91]利用几何形态测量学方法研究中国39个地理种群疣蝗前翅、后翅翅形和大小的差异，并用回归分析探讨造成形态差异的主要环境因素，结果表明种群间前后翅大小存在显著差异，前翅可以划分地理种群，但各地理种群后翅形态差异不大，不能起到划分作用，同时蝗虫的前后翅大小变化遵循伯格曼定律。胡鑫等[92]通过主成分分析、薄板样条分析和ANOVA分析方法，分析中华稻蝗不同龄期功能器官结构的差异，研究表明：后翅、前胸背板、腹板、颜面、后足股节等功能器官存在显著差异，随着龄期的增加，各功能器官非等比例扩大，并通过形成特定形态来实现相应功能。自然选择产生的形态变异增加了物种的多态性和多样性，因此，生态适应与形态变异研究显得尤为重要，在一定程度上能揭示生物进化规律。

3.3 几何形态测量学在直翅目模块集成分析研究中的应用

模块集成研究在直翅目中主要针对昆虫的翅膀，研究结构发育的模块集成有助于理解生物器官结构进化变异进程。Klingenberg等[93]将几何形态测量学技术与进化定量遗传学方法相结合，探讨翅的集成和模块发展问题，结果表明，翅的不同功能区域是集成进化而非模块进化。Coronel等[94]对中华稻蝗Oxyachinensis后翅进行模块集成分析，发现后翅以主脉为边界的翅室是潜在的独立发育模块和形态变异的自主单位，并认为主脉不仅作为边界，也是集成的活跃中心。

3.4 几何形态测量学在直翅目系统发育研究中的应用

厘清生物系统发育关系是生物学家一直进行的工作，但基本以分子数据来研究系统发育，随着几何形态测量学的发展，学者逐渐将形态数据整合到系统发育研究中。和秋菊等[95]基于形态、染色体和解剖特征的40个特征分析竹蝗属Ceracris昆虫的系统发育关系，结果显示，西藏竹蝗最早分化，西藏竹蝗短翅亚种和川南竹蝗最晚分化。García-Navas等[96]以伊比利亚半岛70种蝗虫为研究对象，检验短角蝗不同种之间生态学和系统发育历史的形态差异；同时研究生存环境(地面和植物上)和生态特化水平在塑造形态属性中的潜在作用，结果表明生存环境是短角蝗形态进化的主要驱动力，生存环境和生态特化表现出较强的系统发育保守性，由此提出自然选择在推动物种形成过程中发挥比遗传漂变更重要的作用。Noguerales等[97]结合基因组数据和表型数据分析Chorthippusbinotatus种群进化的系统发育关系和物种界定假说，结果发现表型数据有助于评价生物系统发育关系，表明整合多方面信息检验系统发生假说和阐明物种进化的重要性。总体来说，几何形态测量学方法在直翅目系统发育研究上的应用还有欠缺，其基本是结合其他数据进行研究，甚至仅作为辅助分析的工具，这是因为生物体结构的同源性难以得出准确的系统发育树[98]。Klingenberg等[99]指出，尽管几何形态测量学数据表现出强烈的系统发育信号，但几何形态测量学数据可能不是系统发育的可靠指标。系统发育分析需要有足够多的证据支持才能准确阐明进化中的问题。无论是形态信息还是遗传信息，都不应成为评估系统发育信号的唯一标准[24]。

4 结语

几何形态测量学方法可以测量出生物之间形态结构和大小的差异，揭示种群间的形态变异或表型进化和生态因素之间的关系，其在直翅目中的应用主要集中在分类鉴定和形态变异研究方面，而模块集成分析研究在不断深入，但系统发育分析基本还是基于分子数据研究，单独的形态数据还不足以支撑系统发育分析。随着直翅目研究工作逐步深入，单一方法、简单分析逐渐难以满足研究的需要，为了使研究更具准确性，可整合不同来源的数据解决用单一方法所不及的问题，例如几何形态测量学结合分子数据等。