缺陷对双层扶手型石墨烯纳米带能隙的影响*
2022-10-19王晓丽
王晓丽,龙 文
(首都师范大学物理系,北京 100048)
0 引 言
石墨烯是由碳原子以sp2杂化轨道组成的二维六角晶格[1-2],其准粒子低能激发在狄拉克点附近的色散关系呈线性,其行为与无质量的狄拉克费米子相似[3-4].高纯度石墨烯具有独特的量子流体性质[5-10].石墨烯有许多优良的物理特性,如高强度、高熔点、高电导率、高迁移率和高热导率等,这些性质引起研究者广泛的兴趣和深入的研究[11-15].石墨烯六角晶格由2个不等价子格构成,导带和价带在动量空间的2个不等价狄拉克点以圆锥形相切,这2个狄拉克点手性相反,使得二维石墨烯具有独特的电子特性,如没有背散射,能发生Klein隧穿,具有半整数量子霍尔效应等[16-20].
双层石墨烯保留了许多单层石墨烯的优良特性,层间耦合赋予了其更丰富的能带结构.与单层石墨烯不同,双层石墨烯在费米面附近的色散关系不是线性的[21-22],这使得其具有独特的电子性质,如量子霍尔效应、边态和弱局域性等[12].此外,双层石墨烯还具有不同寻常的光学性质和高导热性.因此,双层石墨烯在下一代纳米电子和光电器件中具有潜在的应用前景,如场效应晶体管、光子器件和热电器件[23].
石墨烯通过机械裁剪可以形成一维或准一维石墨烯纳米带,使其获得非零带隙.根据石墨烯的裁剪方向,石墨烯纳米带有2种基本构型,即扶手型和锯齿型.锯齿型石墨烯纳米带是无能隙的半金属,有弱局域边态[24-28].扶手型石墨烯纳米带没有边态,或者是半金属,或者是半导体,这取决于其带宽[29-31].双层石墨烯的特殊堆叠结构,在某些应用方面甚至优于单层石墨烯.近年来,研究者越来越关注石墨烯双层体系的研究[32-36].双层石墨烯由2个单层石墨烯通过范徳华力耦合在一起,由于范徳华力远小于石墨烯层内的共价键,因此,每层石墨烯可看作多层石墨烯的一个亚单元.每层石墨烯都有2个子格,分别称为A子格和B子格,主要以伯纳尔形式堆叠在一起,简称AB堆叠,即上层的A子格刚好位于下层B’子格上面,上层B子格恰好在下层六角形中心上面,另一种AA堆叠也是一种可能的堆叠方式.AA和AB堆叠具有相同的平移对称性[37-43].但AB堆叠的双层石墨烯有4条能带,其中2条在零能量时接触[44-45],此结构更加稳定[46-49].AA 堆叠的双层石墨烯被认为是亚稳态的,最近才发现了稳定的样品[50-52],因此,AA堆叠结构也引起了研究者的广泛兴趣[53-55].
石墨烯的零带隙限制了其在微纳米电子器件中的应用,调控石墨烯带隙成了凝聚态物理的研究热点[56],双层石墨烯的一个重要特性是,层与层之间的电场可以打开和调节带隙,这与纳米电子学应用高度相关.通过化学掺杂、边无序和加外场等方法也可诱导双层石墨烯的带隙,研究者大多数是通过外加条件调控带隙,但是通过实验方法制备出来的双层石墨烯都存在一些缺陷,对缺陷的引入带来体系性质改变的研究就显得尤为重要[57].
本文拟利用非平衡格林函数方法,研究两端口有限尺寸双层石墨烯纳米带的电子输运,计算有线缺陷时体系的态密度和透射系数.
1 紧束缚模型和公式
双层扶手型石墨烯堆叠类型和含线缺陷单胞结构如图1所示.t0表示层内最近邻原子间的跃迁积分,t1表示上层A原子与下层B’原子间的层间跃迁积分,t2表示上层B原子与下层A’原子的层间跃迁积分,t3表示上层B原子与下层B’原子间的层间跃迁积分.由于t3比t1和t2小,因此,在紧束缚模型中可以将其忽略.t4表示上层A(B)原子与下层A’(B’)原子的层间跃迁积分,带宽N=7.为了避免标号时上下2层格点重叠,将上下2层晶格错开,实际上层格点1恰好在下层格点(15)上,上层格点2恰好在下层格点(16)上,依次类推.本文中均使用黑色表示上层,蓝色表示下层.带宽沿x方向分为N层,每层有2个原子,一个位于A格点,另一个位于B格点,每个单胞含4N个格点,纳米带沿y方向具有周期平移不变性.

图1 双层扶手型石墨烯纳米带堆叠类型和含线缺陷单胞结构(a)AB堆叠;(b)AA堆叠;(c)AB堆叠单胞;(d)AA堆叠单胞
本文研究一个两端口量子输运系统,耦合到左、右导线的双层扶手型石墨烯纳米带结构如图2所示.系统由含1条体线缺陷的AB堆叠双层扶手型石墨烯纳米带构成的通道区和与通道区左、右耦合的2个半无限长纯净双层扶手型石墨烯纳米带导线构成.
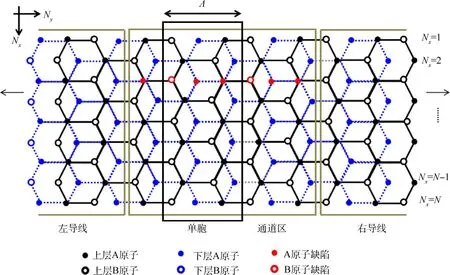
图2 耦合到左、右导线的双层扶手型石墨烯纳米带结构
左、右半无限长导线是纯净的双层扶手型石墨烯纳米带,其中格点的占位能和交叠积分都为常数.左、右导线与通道区通过耦合常数τL和τR直接耦合.中间通道区是含缺陷的双层扶手型石墨烯纳米带,在粒子数表象中其紧束缚哈密顿量可表示为
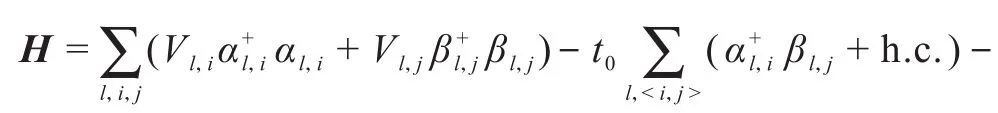
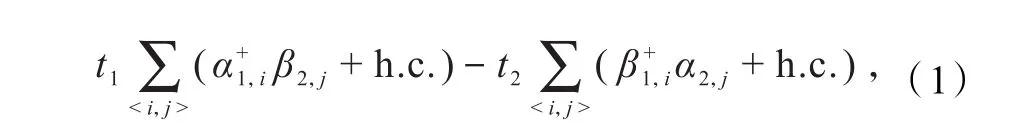
准粒子通过导线-通道区-导线三明治量子相干输运系统的透射系数(T),可以由线宽函数和格林函数通过Fisher-Lee关系表示为
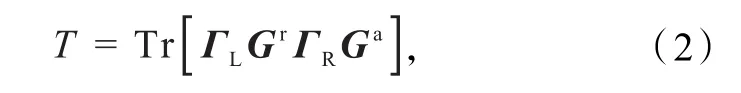
式中:ΓL和 ΓR分别表示与左、右导线耦合的线宽函数,Gr和Ga分别表示通道区的延迟格林函数和超前格林函数.线宽函数可由通道区与左、右导线耦合的延迟自能和表示为
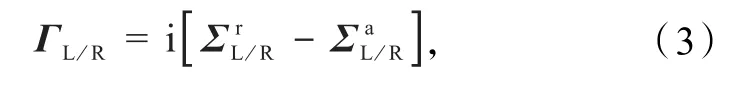
式中i是虚数单位.
将两端导线和中间通道区分解为一系列离散的有效主层,只考虑最近邻主层间的相互作用,通过迭代计算可以得到表面格林函数,进而求出自能.Gr和Ga的表达式为

式中:E表示电子能量,η是一个正的无穷小量,I为单位矩阵.体系的局域态密度(ρDOS)由总线宽函数Γ =ΓL+ΓR得到

本文计算无限长含体线缺陷双层扶手型石墨烯纳米带的能带结构.考虑AB和AA堆叠单胞结构,并让其两端向两侧沿y方向无限延伸.含体线缺陷的无限长双层扶手型石墨烯纳米带等价于一个无限长一维单胞链,满足如下等效差分方程

是双层扶手型石墨烯纳米带的单胞格点波函数,T表示对行波函数求转置.H00和H01分别为单胞占位能矩阵和最近邻交叠积分矩阵,I是单位矩阵,这3个矩阵都是(4N×4N)矩阵.因为纳米带沿y方向具有平移不变性,所以,波函数具有Bloch波形式,式(6)等价于

式中:Λ=3a0是双层扶手型石墨烯纳米带单胞的宽度,a0=0.142 nm是石墨烯碳原子σ键的键长.求解上述方程可得到双层扶手型石墨烯纳米带的能带结构和格点波函数.
2 数值计算
本文分别计算了AB和AA堆叠的无限长双层扶手型石墨烯纳米带的能带谱和波函数,及两端口中间区的透射系数和局域态密度.参数选择为:V0=0,t0=3.160 eV;AB堆叠中,t1=0.390 eV,t2=0.315 eV,由于 t3太小,在计算时将其忽略[58];AA 堆叠中,t4=0.400 eV[59].本文用 V1表示单层缺陷格点占位能,V2(V3)表示上(下)层缺陷格点占位能(缺陷原子占位能取不为0的整数值),分别将缺陷加在纳米带的第L=3(=3m)或 L=5(≠3m)处.
2.1 关闭半导体扶手型石墨烯纳米带能隙
对于单层和双层扶手型石墨烯,在带宽N=3n和N=3n+1时,能隙打开,呈半导体性.有研究表明,同时改变单层半导体扶手型石墨烯的第L=3m条原子的占位能和跃迁积分,可以使能隙关闭[60],但本文研究显示,只改变这2类能带在第L=3m处的占位能就可以使能隙关闭.利用单层的方法,改变AB堆叠双层上下L=3m处原子的占位能,可以使得半导体双层扶手型石墨烯的能带能隙关闭.
关闭单层和双层扶手型半导体石墨烯纳米带能隙的能谱结构如图3所示.当N=9时,能带谱是有能隙的(图3(a)),增大单层纳米带第3条原子的占位能到V1=25 eV,加此缺陷后打破了晶格间的对称性,能带谱的能隙几乎关闭,当占位能增大到一定数值,能隙可以完全关闭(图3(b)).由于层间相互作用使得单层的二重简并性被破坏,能带被分裂成4条,可以清晰地看到能带谱是有能隙的,并且双层纳米带能谱在狄拉克点处呈现抛物线型(图3(c)),增大双层纳米带上下层第3条原子的占位能到V2=V3=25 eV,加此缺陷后能隙几乎关闭,当占位能增大到一定数值,能隙可完全关闭(图3(d)).对于AB堆叠结构,增加带宽(N=15)不能使能隙关闭(图3(e)).N=9(N≠3n+2)的 AA堆叠双层扶手型石墨烯纳米带能带结构有能隙,如图3(f)所示.由于AA堆叠稳定性弱于AB堆叠稳定性,施加一个比AB堆叠更小的占位能,就可以使得能带谱的能隙几乎关闭.增大AA堆叠双层纳米带上下层第3条原子的占位能到V2=V3=20 eV(<25 eV)时,能隙可以完全关闭(图3(g)).由于AA堆叠不稳定,也可以通过增加带宽(N=15)关闭能隙(图3(h)).
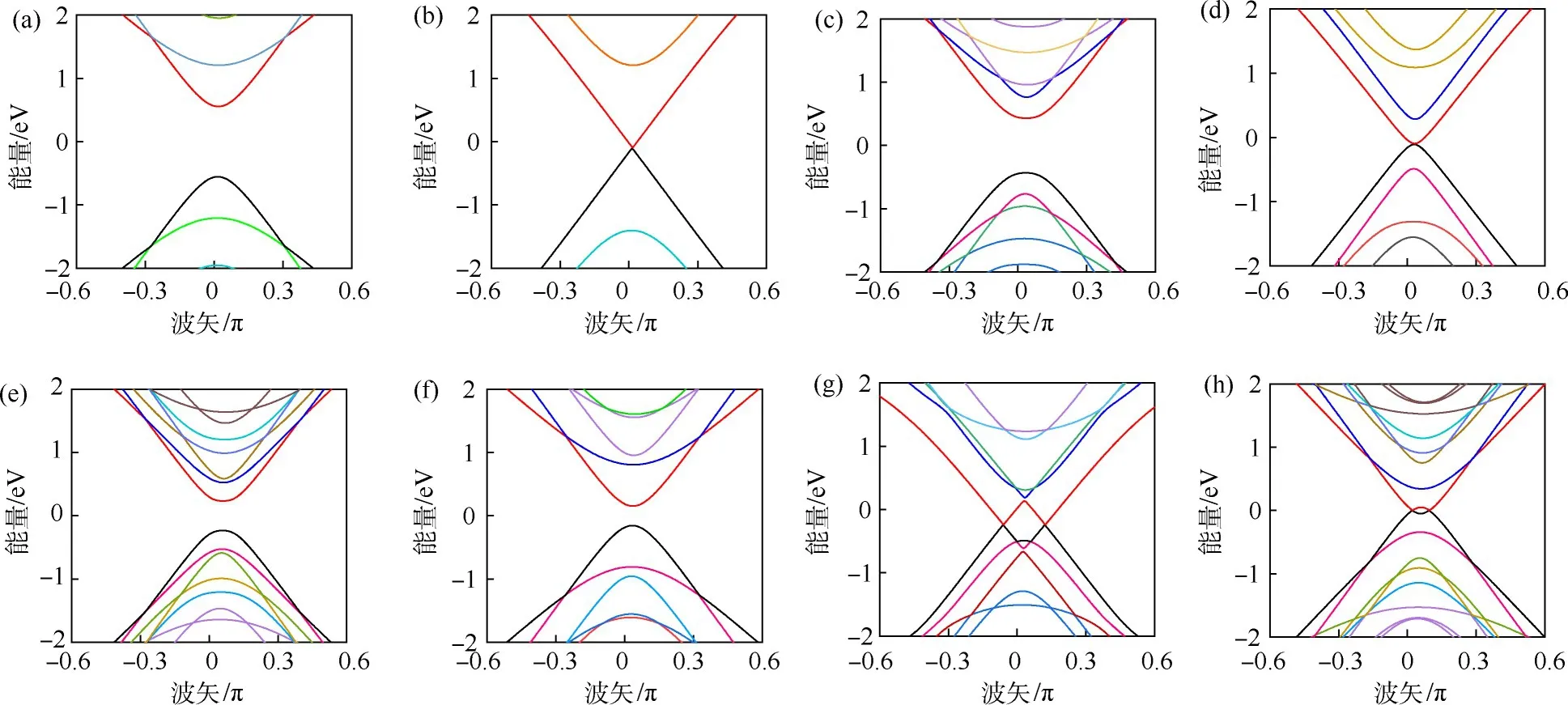
图3 关闭半导体扶手型石墨烯纳米带单层和双层的能谱结构(a)单层石墨烯纳米带,V1=0,N=9;(b)单层石墨烯纳米带,V1=25 eV,N=9;(c)AB堆叠石墨烯纳米带,V2=V3=0,NAB=9;(d)AB堆叠石墨烯纳米带,V2=V3=25 eV,NAB=9;(e)AB堆叠石墨烯纳米带,V2=V3=0,NAB=15;(f)AA堆叠石墨烯纳米带,V2=V3=0,NAA=9;(g)AA堆叠石墨烯纳米带,V2=V3=20 eV,NAA=9;(h)AA堆叠石墨烯纳米带,V2=V3=0,NAA=15
关闭单层和双层扶手型半导体石墨烯纳米带能隙的透射系数和态密度如图4所示.无缺陷带宽N≠3n+2时,单层扶手型石墨烯纳米带在E=0附近的一个有限区间内透射系数和态密度的值均为0,表明此时存在一个有限能隙(图4(a)),添加缺陷后,单层扶手型石墨烯纳米带在E=0附近的一个有限区间内,零值几乎消失,变为有限值,说明能隙几乎关闭(图 4(b)).当无缺陷带宽 N≠3n+2时,AB堆叠双层扶手型石墨烯纳米带在E=0附近的一个有限区间内值为0,说明此时存在一个有限能隙(图4(c)),添加缺陷后,AB堆叠双层扶手型石墨烯纳米带在E=0附近的一个有限区间内零值几乎消失,变为有限值,说明能隙几乎关闭(图4(d)),只增大带宽时,AB堆叠双层扶手型石墨烯纳米带在E=0附近的一个有限区间内值仍然为0,说明增大带宽后能隙未关闭(图 4(e)).无缺陷带宽N≠3n+2时,AA堆叠双层扶手型石墨烯纳米带在E=0附近的一个有限区间内值为0,说明此时存在一个有限能隙(图4(f)),添加缺陷后,AA堆叠的双层扶手型石墨烯纳米带在E=0附近的一个有限区间内零值全部消失,变为有限值,说明能隙完全关闭(图4(g)),随着带宽的增加,AA堆叠纳米带在E=0附近的一个有限区间内零值全部消失,变为有限值,说明带宽的增加可以使AA堆叠双层扶手型石墨烯纳米带能隙完全关闭(图4(h)),这与本文能带图的结论是一致的.
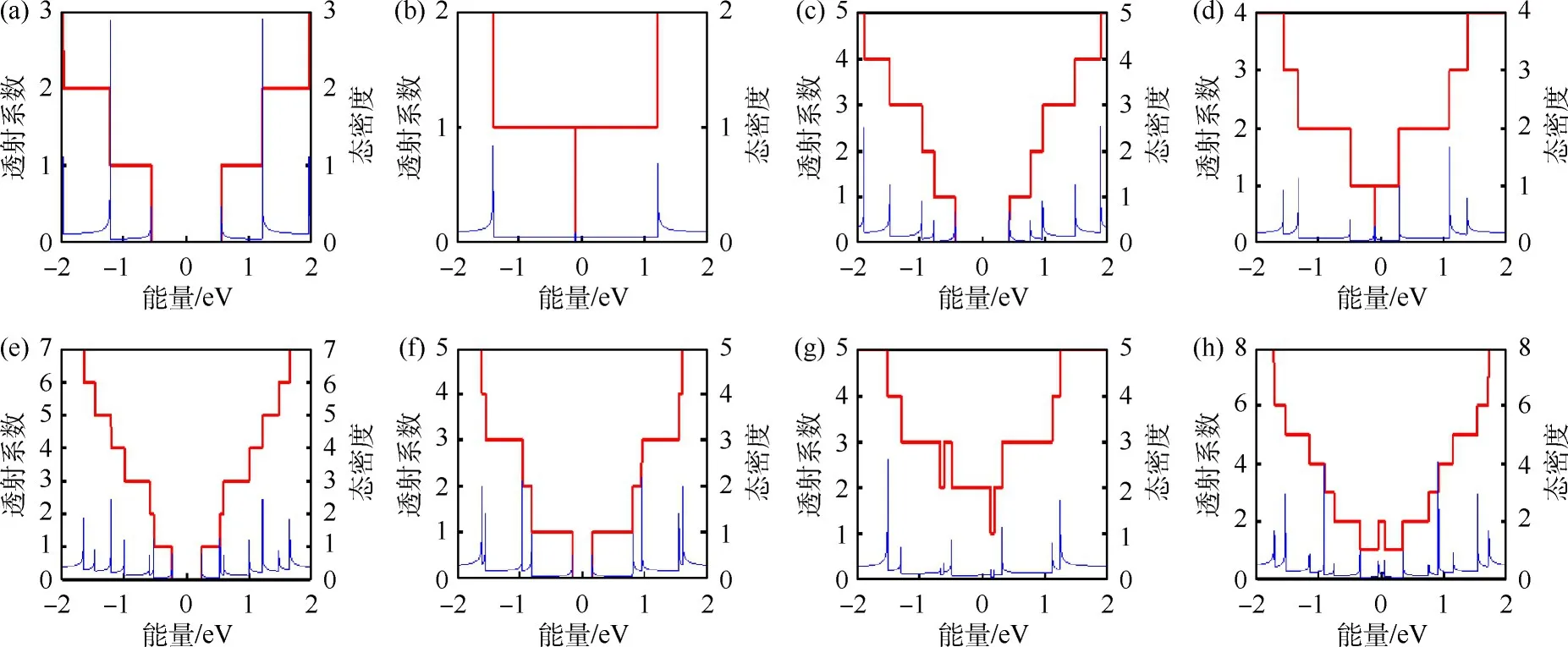
图4 关闭单层和双层扶手型半导体石墨烯纳米带能隙的透射系数和态密度(a)单层石墨烯纳米带,V1=0,N=9;(b)单层石墨烯纳米带,V1=25 eV,N=9;(c)AB堆叠石墨烯纳米带,V2=V3=0,NAB=9;(d)AB堆叠石墨烯纳米带,V2=V3=25 eV,NAB=9;(e)AB堆叠石墨烯纳米带,V2=V3=0,NAB=15;(f)AA堆叠石墨烯纳米带,V2=V3=0,NAA=9;(g)AA堆叠石墨烯纳米带,V2=V3=20 eV,NAA=9;(h)AA堆叠石墨烯纳米带,V2=V3=0,NAA=15
关闭单层和双层扶手型半导体石墨烯纳米带能隙的波函数模如图5所示.单层加入缺陷使得电子整体分布不均匀,对于价带顶的波函数模出现边缘态,电子几乎分布在纳米带缺陷处的上层部分,而对于导带底电子几乎分布在纳米带缺陷处的下层部分,并且随波矢的变化不明显(图5(a)和(b)).AB堆叠双层加入缺陷使得上下层电子整体分布不均匀,对于价带顶的波函数模在上下层都出现边缘态,电子几乎分布在纳米带缺陷处的上面条带部分,而对于导带底上下层电子几乎分布在纳米带缺陷处的下面条带部分,并且随波矢的变化不明显(图5(c)和(d)).AA堆叠双层加入缺陷使得上下层电子整体分布不均匀,并且随波矢变化,对于波矢ky=0时,价带顶的波函数模在上下层都出现边缘态,电子几乎分布在纳米带缺陷处的上面条带部分,而对于波矢ky=0.1π和0.2π时,导带底的波函数模在上下层都出现边缘态,上下层电子几乎分布在纳米带缺陷处的上面条带部分(图5(f)和(g)).增大带宽,不管是AB还是AA堆叠,波函数模的整体规律不变(图5(e)和(h)).

图5 关闭单层和双层扶手型半导体石墨烯纳米带能隙的波函数模(a)单层石墨烯纳米带,V1=0,N=9;(b)单层石墨烯纳米带,V1=25 eV,N=9;(c)AB堆叠石墨烯纳米带,V2=V3=0,NAB=9;(d)AB堆叠石墨烯纳米带,V2=V3=25 eV,NAB=9;(e)AB堆叠石墨烯纳米带,V2=V3=0,NAB=15;(f)AA堆叠石墨烯纳米带,V2=V3=0,NAA=9;(g)AA堆叠石墨烯纳米带,V2=V3=20 eV,NAA=9;(h)AA堆叠石墨烯纳米带,V2=V3=0,NAA=15
2.2 打开扶手型金属石墨烯纳米带能隙
对于单层和双层扶手型石墨烯,在带宽N=3n+2时,能隙关闭,呈金属性.有研究显示,同时改变单层扶手型金属性石墨烯第L≠3m条原子的占位能和跃迁项可以使得能带能隙打开[60],但本研究表明,只改变这类能带在第L≠3m处的占位能就可以使得能隙打开,利用单层的方法改变AB和AA堆叠上下层第L≠3m处原子的占位能,可以使得金属型双层扶手石墨烯的能带能隙打开.
打开单层和双层扶手型金属石墨烯纳米带能隙的能带结构如图6所示,带宽N=11.单层纯净(无缺陷)扶手型石墨烯能带谱是无能隙的(图6(a)),增大单层纳米带第5条A原子的占位能为V1=1.264 eV,能带谱的能隙打开(图6(b)).AB堆叠的双层纯净扶手型石墨烯能带谱是无能隙的(图6(c)),增大双层纳米带上下层第5条A原子的占位能为V2=V3=1.264 eV,加缺陷可以使得能带谱的能隙打开(图6(d)).AA堆叠的双层纯净扶手型石墨烯能带谱是无能隙的(图6(e)),增大双层纳米带上下层第5条A原子的占位能为V2=V3=3 160 eV,可以清晰地看出能带谱是无能隙的,并且出现了2条平整的平带(图6(f)).同时改变AA堆叠的上下层第5条A原子和B原子的占位能为V2=-7.900 eV,V3=7.900 eV,能带谱无能隙,并且出现了2条几乎平整的平带,如图 6(g)所示 .
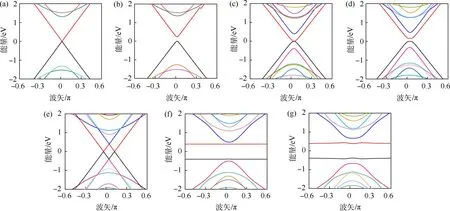
图6 打开单层和双层扶手型金属石墨烯纳米带能隙的能带结构(a)单层石墨烯纳米带,V1=0;(b)单层石墨烯纳米带,V1=1.264 eV;(c)AB堆叠石墨烯纳米带,V2=V3=0,NAB=11;(d)AB堆叠石墨烯纳米带,V2=V3=1.264 eV;(e)AA堆叠石墨烯纳米带,V2=V3=0,NAA=11;(f)AA堆叠石墨烯纳米带,V2=V3=3 160 eV;(g)AA堆叠石墨烯纳米带,V2=-7.900 eV,V3=7.900 eV
打开单层和双层扶手型金属石墨烯纳米带能隙的透射系数和态密度如图7所示,带宽N=11.对于无缺陷带宽N=3n+2,单层扶手型石墨烯纳米带在E=0附近的一个有限区间内为有限值,说明此时能隙是关闭的(图7(a)),当添加缺陷后,单层扶手型石墨烯纳米带在E=0附近的一个有限区间内值变为0,这说明能隙打开(图7(b)).AB堆叠的双层扶手型石墨烯纳米带在E=0附近的一个有限区间内为有限值,此时能隙是关闭的(图7(c)),当添加缺陷后,AB堆叠的双层扶手型石墨烯纳米带在E=0附近的一个有限区间内值变为0,这说明能隙打开(图7(d)).无缺陷时,AA堆叠双层扶手型石墨烯纳米带在E=0附近的一个有限区内透射系数和态密度的值都为有限值,此时能隙关闭(图7(e)).添加缺陷后,AA堆叠的双层扶手型石墨烯纳米带在E=0附近的一个有限区间内值变为0,这说明能隙打开,并且在费米面附近有一个尖的态密度峰,这正是2条平带贡献(图 7(f)和 7(g)).
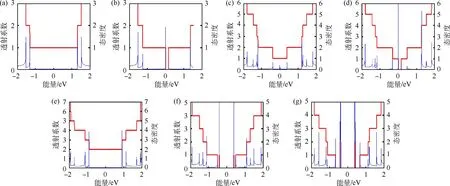
图7 打开单层和双层扶手型金属石墨烯纳米带能隙的透射系数和态密度(a)单层石墨烯纳米带,V1=0;(b)单层石墨烯纳米带,V1=1.264 eV;(c)AB堆叠石墨烯纳米带,V2=V3=0,NAB=11;(d)AB堆叠石墨烯纳米带,V2=V3=1.264 eV;(e)AA堆叠石墨烯纳米带,V2=V3=0,NAA=11;(f)AA堆叠石墨烯纳米带,V2=V3=3 160 eV;(g)AA堆叠石墨烯纳米带,V2=-7.900 eV,V3=7.900 eV
打开单层和双层扶手型金属石墨烯纳米带能隙的波函数模如图8所示,带宽N=11.单层加入缺陷电子整体仍然均匀分布(图8(a)和(b)).AB堆叠双层加入缺陷使得ky=0上下层电子分布的对称性发生改变,未加缺陷时对于导带底电子几乎分布在纳米带下层部分,而价带顶电子几乎分布在纳米带的上层部分,加缺陷后对于导带底电子几乎分布在纳米带上层部分,而价带顶电子全部分布在纳米带的下层部分,上层部分电子概率严格为0,这使得在狄拉克点处导带底与价带顶之间的量子输运通道被打破,并且随波矢的增大电子整体呈均匀分布(图8(c)和(d)).AA堆叠双层只加入A原子缺陷价带顶上下层电子整体仍然呈均匀分布,而导带底的上下层电子分布对称性被破坏,电子分布不均匀(图 8(e)和(f)).AA堆叠双层同时加入 A原子和B原子缺陷时,价带顶和导带底上下层电子整体呈不均匀分布,并且随着波矢的增大导带底的下层的电子占据概率增大,上层电子概率减小,而价带顶的上层的电子占据概率增大,下层电子概率减小(图 8(g)).

图8 打开单层和双层扶手型金属石墨烯纳米带能隙的波函数模(a)单层石墨烯纳米带,V1=0;(b)单层石墨烯纳米带,V1=1.264 eV;(c)AB堆叠石墨烯纳米带,V2=V3=0,NAB=11;(d)AB堆叠石墨烯纳米带,V2=V3=1.264 eV;(e)AA堆叠石墨烯纳米带,V2=V3=0,NAA=11;(f)AA堆叠石墨烯纳米带,V2=V3=3 160 eV;(g)AA堆叠石墨烯纳米带,V2=-7.900 eV,V3=7.900 eV
3 结 论
基于单电子紧束缚模型,研究了线缺陷对无限长AB和AA堆叠双层扶手型石墨烯纳米带能谱的影响,特别是对能隙的调控,并与体线缺陷对单层扶手型石墨烯纳米带能隙调控对比,讨论了带宽对AA和AB堆叠双层扶手型半导体带的影响.利用格林函数方法,计算了相应的透射系数和局域态密度.
数值计算表明,纳米带能隙的调控依赖于线缺陷的位置、类型和强度.对于半导体单层和双层扶手型石墨烯纳米带,其能隙的打开和关闭依赖于子格线缺陷的位置和强度.当改变单层和双层第L=3m处原子的占位能时,随着占位能的增大可以使能隙最终完全关闭;对于AA堆叠的双层扶手型石墨烯纳米带,不但加线缺陷可以关闭能隙,增加带宽也能关闭能隙,但增加带宽不能关闭AB堆叠扶手型半导体纳米带的能隙.对于金属性单层和双层扶手型石墨烯纳米带,增加第L≠3m处A原子占位能可打开能隙.对于AA堆叠金属性扶手石墨烯,增大第L≠3m处A原子占位能不仅能打开能隙,而且当占位能达到一定值时,能带中会出现很清晰的平带,当同时改变第L≠3m处的A、B原子的占位能时,很小的占位能就可在能带中形成一条几乎平整的平带.为了进一步证实本文结果,计算了相应的透射系数和局域态密度,结果与能带谱计算结果一致.本文的研究加深了对双层扶手型石墨烯纳米带的认识,为设计双层石墨烯基量子器件提供了理论支持.
