移动边缘计算分布式保护业务部署算法
2022-10-19李泳成宗红梅林玠珉孟二帅符小东房洪莲沈一春
李泳成,宗红梅,林玠珉,孟二帅,符小东,房洪莲,沈一春
(1.苏州大学 电子信息学院,江苏 苏州 215006; 2. 中天通信技术有限公司,江苏 南通 226000;3. 中天宽带技术有限公司,江苏 南通 226463; 4. 中天科技精密材料有限公司,江苏 南通 226009)
0 引 言
随着第五代移动通信技术(5th Generation Mobile Communication Technology,5G)的成熟,诸如物联网、车联网等资源密集、时延敏感型业务快速增长。移动边缘计算(Mobile Edge Computing, MEC)通过在网络边缘部署边缘数据中心,就近为用户提供计算和存储资源,被认为是承载这些新兴业务的重要技术之一[1]。同时,MEC也存在单个边缘数据中心内计算和存储资源有限,缺乏为大量并发业务提供服务的能力。因此,MEC中存在一类业务可以通过切分成多个子业务,以分布式的形式在不同数据中心中执行,称为MEC分布式业务[2]。目前,针对MEC分布式业务的研究主要集中在业务切分和计算卸载[3-5],而缺乏对该类业务保护问题的研究。本文针对MEC分布式业务保护问题展开了深入研究。通过结合专用保护技术[6],本文以最小化总业务时延为目标,构建了整数线性规划(Integer Linear Programing,ILP)模型,并提出了基于轮询的MEC分布式专用保护业务部署算法。仿真结果表明,本文所提启发式算法能有效降低业务总时延和均衡MEC服务器间的负载,且与ILP模型获得的最优结果十分接近。
1 MEC分布式专用保护业务部署
1.1 问题定义
在MEC网络中,服务器、无线接入点和光纤链路故障都可能导致MEC分布式业务无法完成。为此,需要为MEC分布式业务提供保护以提高其生存性。本文结合专用保护技术,为每一个子业务都部署专属保护子业务,即MEC分布式专用保护业务。首先,对MEC网络做如下假设:(1) 网络中每个节点上存在一个MEC服务器,其单位时间t内可用计算资源为N个单位;(2) 完成所有业务可用的总时隙为T;(3) 每个MEC分布式专用保护业务选择最近的m个MEC服务器部署;(4) 本文中采用最短路由算法选出最近的m个MEC服务器;(5) 单个业务的时延为所有子业务和保护子业务完成的最大时延。
图1所示为一个MEC分布式专用保护业务部署的实例。假设每个时隙下,每个MEC服务器可用计算资源为3个单位。业务u的子业务S1(3个单位)、S2(5个单位)、S3(4个单位)和S4(4个单位)已分别部署到4个MEC服务器上(N0、N1、N2和N3)。现给出两种方案部署业务u的保护子业务。方案1为S1在N3上部署了保护子业务P1(3个单位)、为S2在N2上部署保护子业务P2(5个单位)、为S3在N1上部署保护子业务P3(4个单位),为S4在N2上部署保护子业务P4(4个单位)。而方案2则为S1在N2上部署了保护子业务P1(3个单位)、为S2在N3上部署保护子业务P2(5个单位)、为S3在N0上部署保护子业务P3(4个单位),为S4在N1上部署保护子业务P4(4个单位)。显然,第2种部署方案所需的总业务时延为3个时隙,而方案1则为5个时隙,且方案2各个MEC服务器之间的负载更加均衡。为此,需要为MEC分布式保护业务提出高效的优化部署方案,以降低总业务时延,均衡各个MEC服务器之间的负载。
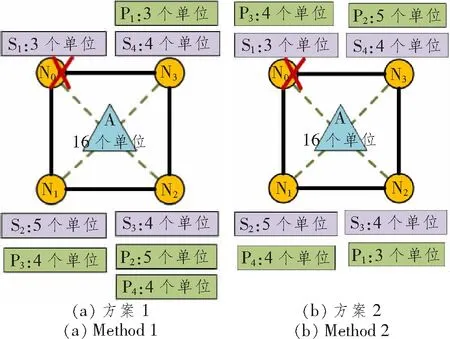
图1 MEC分布式专用保护业务实例Figure 1 Case of MEC distributed dedicated protection service
1.2 ILP模型
结合以上关于MEC分布式专用保护业务部署的问题描述,本文通过将问题进行数学抽象,以最小化业务总时延为目标,构建了一个ILP优化模型。该模型将问题涉及的限制条件和目标用数学公式表达,能够为该问题在求解域内搜寻到满足所有限制条件的理论最优解。所构建模型的具体推导过程如下:
首先,将该问题涉及到的集合,进行数学抽象,包括MEC网络中的节点集合,业务集合,每个业务所包含的子业务集合,每个业务可用的MEC节点集合,以及所有可用时隙的集合。其次,将该问题涉及到的参数进行数学抽象,包括每个MEC节点单位时间内允许提供的计算资源,每个子业务需要MEC节点提供的计算资源。最后,对该问题需要设立的变量进行整理,包括总业务时延以及为求解该目标值所依赖的其他变量。基于以上思路,定义本文ILP模型的集合、参数和变量如下:
(1) 集合
U: MEC网络中分布式业务集合。
E: MEC网络中节点集合。
Ku: MEC分布式业务u的子业务集合。
Eu: MEC分布式业务u可用的MEC节点集合。
T: 可用时隙集合。
(2) 参数
Ru: MEC分布式业务u所需的MEC计算资源,u∈U。
Ve: MEC节点e上单个时隙内提供的MEC计算资源。
Δ: 一个极大值。
(3) 变量
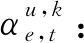



Γ: 整型变量,总业务时延。
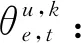
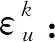
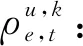
优化目标:最小化Γ。
接下来,需要进一步明确该模型所需满足的限制条件。为此,本文考虑4个主要内容:每个业务的子业务都被成功在MEC节点上部署;每个子业务的保护业务被成功在MEC节点上部署;单个时隙内,每个MEC节点提供的计算资源不能超过其最大计算资源;总业务时延的计算方法。基于以上思路,本文将限制条件表示如下:
(1) 子业务约束
(2) 保护子业务约束
(3) MEC服务容量约束
(4) 业务总时延
式(1~2)表示任意业务的一个子业务只能使用一个MEC服务器。式(3)表示任意业务的所有子业务必须部署到不同MEC服务器上,其中,e1和e2为集合Eu中任意两个MEC节点,t1和t2为集合T中任意两个时隙。式(4)确认业务的子业务在每个时隙内占用的MEC服务器的计算资源。式(5)表示MEC服务器子业务提供的计算资源。式(6)表示任意业务所有子业务占用计算资源量总和等于该业务计算资源需求。式(7)表示任意子业务与其保护子业务不能部署到同一MEC服务器上。式(8)表示任意业务的一个子业务的保护子业务只能使用一个MEC服务器。式(9~11)表示任意业务的某个子业务占用的计算资源与其保护子业务占用的计算资源相同。式(12)表示在某个时隙,MEC服务器被占用的计算资源之和不能超过其可提供最大计算资源。式(13~14)表示业务总时延不小于任意业务的子业务及其保护子业务的完成时间。

2 基于轮询的启发式算法
由于ILP模型难以有效求解大规模问题,为此,本文也提出了部署MEC分布式专用保护业务的启发式算法,包括随机部署、环部署和双轮询部署。这3种算法都采用了轮询策略进行子业务的切分和部署。具体地,为业务每一个计算需求(单位:unit)在单个时隙内轮询所有可用MEC服务器,一旦某个MEC服务器上存在空闲计算资源,则将该计算需求部署在该MEC服务器上。如果当前时隙下没有可用计算资源,则进入下一个时隙重复以上过程。当业务的所有计算需求单元都完成部署,则查看每一个MEC服务器上部署的总计算需求单元,即为切分的子业务。
不同的是,随机算法为每一个子业务随机选择MEC服务器部署专属保护子业务。环部署算法则顺序将当前子业务的专属保护子业务部署到下一个MEC服务器上。双轮询部署算法也采用了轮询的方式部署子业务的保护子业务。该算法的核心思想是通过尽可能均匀地在各个MEC服务器上部署工作和保护子业务,从而实现最小化总业务时延。接下来,详细介绍双轮询MEC分布式专用保护业务部署算法。
遍历网络中所有业务集合U,对于每一个业务u执行如下操作:
(1) 采用最短路由算法获取与业务u所在本地节点最近的n个MEC服务器加入业务u的可用MEC服务器集合Eu。
(2) 遍历业务u计算资源请求集合Su,对于每一个计算资源s(1个单元)执行如下操作:
(a) 令时隙索引t=0,计算资源索引v=0。
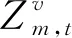
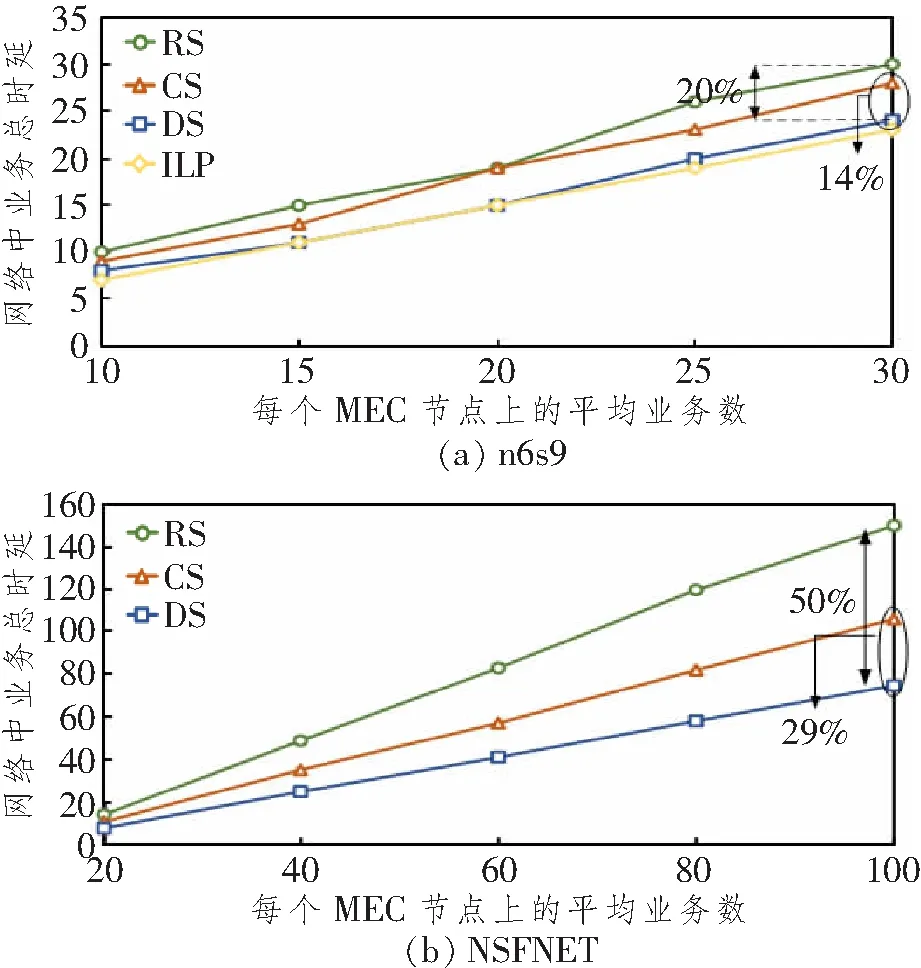
(c) 若所有MEC服务器都无法部署s,则令v=v+1,若v (d) 否则,s被成功部署到MEC服务器m*,为其部署对应的保护计算资源s'。 令时隙索引t=0,计算资源索引r=0,遍历集合Eu/m*,对于每一个m执行如下操作: 若所有MEC服务器都无法部署s',则令v=v+1,若r 对比以上3种算法,随机算法随机性较强,容易导致部分子业务集中到某一个MEC服务器上。环部署算法虽然更加侧重均衡,但因为没有考虑不同子业务的时延,仍然会导致为部分MEC服务器提供更多的计算资源,从而增加总业务时延。双轮询部署算法将子业务和保护子业务分别通过轮询的方式部署到MEC服务器上,能有效均衡各个MEC服务器承载的业务,从而降低总的业务时延。 本文评估了MEC分布式专用保护业务部署算法在业务总时延和负载均衡方面的性能。采用6个节点、9条链路的n6s9和14个节点、23条链路的NSFNET两个测试网络[7]进行了仿真。仿真条件如下:网络中每个节点上都部署一个MEC服务器,每个MEC服务器上单个时隙内最大可用计算资源为1 000;总的时隙数设为200;n6s9网络中每个MEC节点业务数在[X-5,X]范围内随机产生,NSFNET中每个MEC节点业务数在[X-20,X]范围内随机产生,X为每个MEC节点上的平均业务数。每个业务所需的计算资源为400;业务最大切分数量为4。每个业务可选择的MEC服务器通过最短路由算法(Dijkstra's)获得。本文利用AMPL/Gurobi[8]软件求解ILP优化模型,并采用Java语言实现启发式算法。 图2所示为不同部署算法的业务总时延。图中,“ILP”表示ILP优化模型的结果;“RS”、“CS”和“DS”分别对应随机部署算法、环部署算法和双轮询部署算法的结果。由图2(a)可知,随着每个MEC节点上平均业务数量的增加,ILP优化模型和3种调度策略的网络业务总时延逐渐增大。这是因为大量的业务意味着需要占用服务器更多的计算资源,从而增加了业务完成的时延。比较不同部署算法,发现双轮询算法与ILP模型结果十分接近,远远小于RS和CS算法的业务总时延。当每个节点上的平均业务数为30时,与RS和CS算法相比,双轮询算法减少了20%和14%的业务总时延。本文在NSFNET中也做了类似仿真。如图2(b)所示,双轮询算法的业务总时延总是低于随机和环部署算法。当每个节点上平均业务数为100时,双轮询算法的业务总时延比RS和CS算法分别少了50%和29%。以上结果证明了双轮询部署算法在减少业务总时延方面的高效性。 图2 网络中业务总时延Figure 2 Total service delay in the network 本文也比较了不同部署算法的MEC服务器负载均衡性能。图3所示为n6s9和NSFNET中MEC服务器负载的方差。其中n6s9节点上业务数在[10,50]范围内随机产生,NSFNET节点上的业务数在[20,100]范围内随机产生。纵轴是服务器上承载的总的计算需求(负载)。发现双轮询算法的MEC服务器负载方差最小(1.48),远低于使用RS和CS算法的MEC服务器负载方差(6.28和4.47)。类似地,如图3(b)所示,双轮询算法在NSFNET中实施后,MEC服务器负载方差仅为5.9,远低于RS和CS算法的19.4和13.2。这是因为双轮询算法在为子业务和保护子业务选择MEC服务器时,都充分考虑了每个MEC服务器的负载情况,因此能更好地均衡各个MEC服务器间的负载。 图3 网络中MEC服务器上的负载Figure 3 Load on MEC servers in the network 本文研究了MEC中分布式专用保护业务的部署问题,以最小化业务总时延为目标,构建了相应的ILP模型,并提出了高效的启发式算法,包括随机、环和双轮询部署算法。仿真结果表明,本文提出的双轮询部署算法既能有效降低总业务时延,也能均衡MEC服务器间的负载。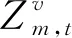
3 结果与性能分析
3.1 测试条件
3.2 结果分析
3.3 负载均衡

4 结束语
