基于定积分的放疗权重因子自动优化方法研究

郭彩萍 张俊生 张晓娟

1(太原工业学院电子工程系，太原 030008)2(中北大学信息与通信工程学院，太原 030005)

引言

保护正常组织(normal tissue， NT)和危及器官(organs at risk， OAR)的同时，给予靶区(planning target volume， PTV)尽可能高均匀剂量是调强放射治疗(intensity modulated radiation therapy， IMRT)的矛盾所在[1]。 由于逆向调强的可靠性高、实用性强和效率高，目前广泛使用这种技术获得矛盾之间的平衡。

在标准的逆向调强注量图优化(fluence map optimization， FMO)中，通常通过最小化加权和目标函数方法获得这种平衡。 其中，目标函数权重因子的确定方法有两种:人工试误的方法[2-3]和多目标优化方法(multi-objective optimization， MOO)[4-5]。由于多目标优化优化时间太长，尽管采用试误的方法获得一组合适的权重因子需要物理师漫长的试错过程，但仍然是放疗实践中最常用的方法。 而且，随着目标函数中子目标函数的数量增加，人工试误方法将变得更加复杂。 为了提高逆向调强的效率，迫切需要提出高效的权重因子自动优化方法。

一些自动优化权重因子的方法已经被研究者们提出。 Xing 等[6]提出了由预定剂量体积分布图(dose volume histogram，DVH)评分函数引导的两步权重因子自动优化方法。 采用相似的方法，一些研究者们提出了由参考计划引导的自动优化方法[7-13]。 对于不同的临床应用，参考计划的来源是不同。 对于自动再计划，参考计划来自于病人的原始计划；对于基于专家库的优化，参考计划来自于放疗数据库。 这些方法都能够自动调整权重因子，但是需要提前为每个放疗组织预选一条DVH 参考曲线。 由于患者放疗期间解剖结构的变化和患者之间解剖结构的差异性，为逆向计划提前预选理想的DVH 曲线是一件困难的事情。 另外一些研究者们采用机器学习的方法估计OAR 的DVH 曲线和权重因子，这种方法需要大量的临床病例训练模型，在少发肿瘤治疗的临床应用上受到限制[14-17]。 Dias等[18]提出了基于模糊推理理论同时调整处方剂量和权重因子的方法，该方法需要设置复杂的隶属度函数。

受定积分理论的启发，本研究提出一种简单自动优化权重因子的方法，新方法能够获得不劣于人工计划质量的自动计划，提高放疗计划效率。

1 材料和方法

1.1 材料

所采用的剂量计算方法、仿真软件CERR 平台和优化算法同文献[19]，算法在Matlab 平台上实现。

1.2 自动优化方法

自动迭代调整权重因子是方法的核心所在。图1 描绘了新自动优化方法的流程，主要包括三方面内容:(1)根据提出的权重因子调整策略自动迭代调整权重因子，如图中矩形框I 所示；(2)迭代完成后，根据评价准则评估所得计划是否临床接受；(3)如果可以接受，结束优化过程；否则通过引入额外的补偿系数，赋予未满足剂量目标相关的子目标函数更高惩罚，然后重复上述步骤直到生成满意计划，如图中矩形框II 所示。

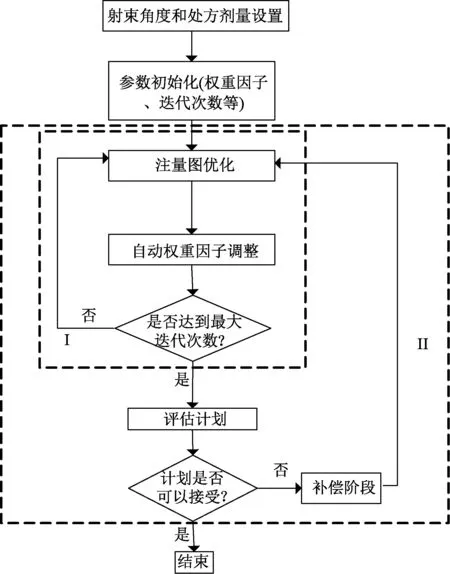
图1 自动优化方法流程Fig.1 Overview of the automatic optimization method

1.2.1 权重因子调整策略

物理放疗优化中使用的物理准则有:最小剂量、最大剂量、平均剂量、最小DVH 和最大DVH。最小剂量准则和最大剂量准则是DVH 准则的特例。用wold和wnew分别代替调整前和自动调整后的权重因子，二者的关系如式(1)所示。

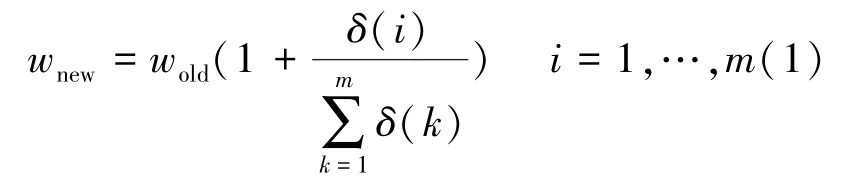
式中，m代表总目标函数中子目标函数的个数，即权重因子的个数；δ(i) 代表第i个子目标函数权重因子的纠正因子，其大小由不满足约束条件DVH 区域的面积决定。 不同的物理准则，权重纠正因子的调整策略不一样。

1)最大DVH 准则

最大DVH 约束条件为V(D ＞D1)＜V1，即组织内接受剂量大于D1的体积应该小于V1。 图2 中实线表示理想DVH 曲线，虚线表示实际DVH 曲线。图2 中所示阴影部分，表示接受的实际剂量大于D1的组织体积不小于处方体积V1， 不满足约束条件V(D ＞D1)＜V1。 不满足约束条件阴影部分面积δDVHmax的定义如式(2) 所示。 实际剂量曲线上V(D2)＝V1，V(D1)＝V2；Vcur(t)代表当前DVH 曲线在剂量t处的体积。

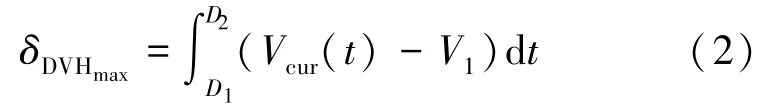
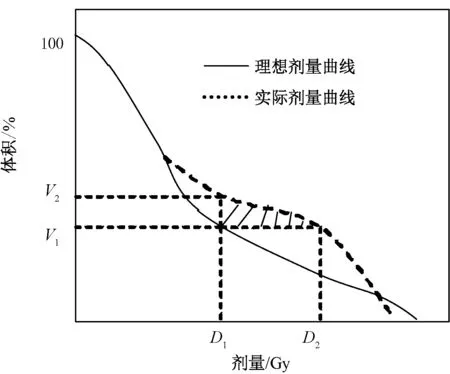
图2 最大DVH 准则Fig.2 Maximum DVH criterion

2)最小DVH 准则

最小DVH 约束为V(D ＞D1)＞V1，即组织内接受剂量大于D1的体积应该大于V1。 图3 中阴影部分，表示接受的实际剂量小于D1的组织体积小于处方体积V1，不满足约束条件V(D ＞D1)＞V1。阴影部分面积δDVHmin用式(3)求出，Vpre(t)代表处方DVH 曲线在剂量t处的体积。

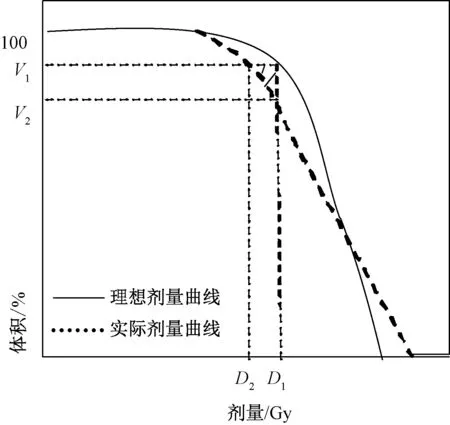
图3 最小DVH 准则Fig.3 Minimum DVH criterion

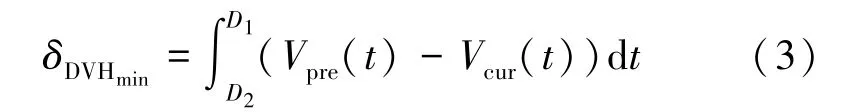
3)最小剂量Dmin

最小剂量准则相当于最小DVH 中Vpre(t ＝Dmin)＝1 和D1＝Dmin的情况。 此时不满足约束条件区域的面积δDmin用式(4)表示。

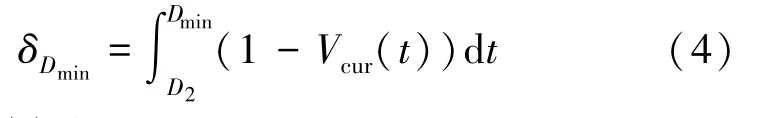
4)最大剂量Dmax

最大剂量准则相当于最大DVH 中V1(D1＞Dmax)＝0 的情况。 此时违反约束条件区域的面积δDmax用式(5)表示。

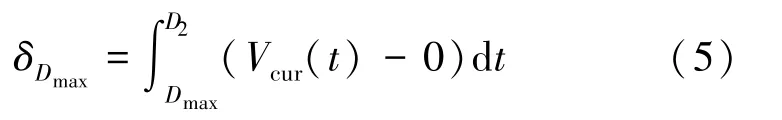
5)平均剂量Dmean

平均剂量准则常用来描述靶区剂量的均匀分布程度。 图4 中实线和虚线分别代表理想和实际的靶区DVH 曲线，不满足约束阴影区域的面积δDmean用式(6)表示。

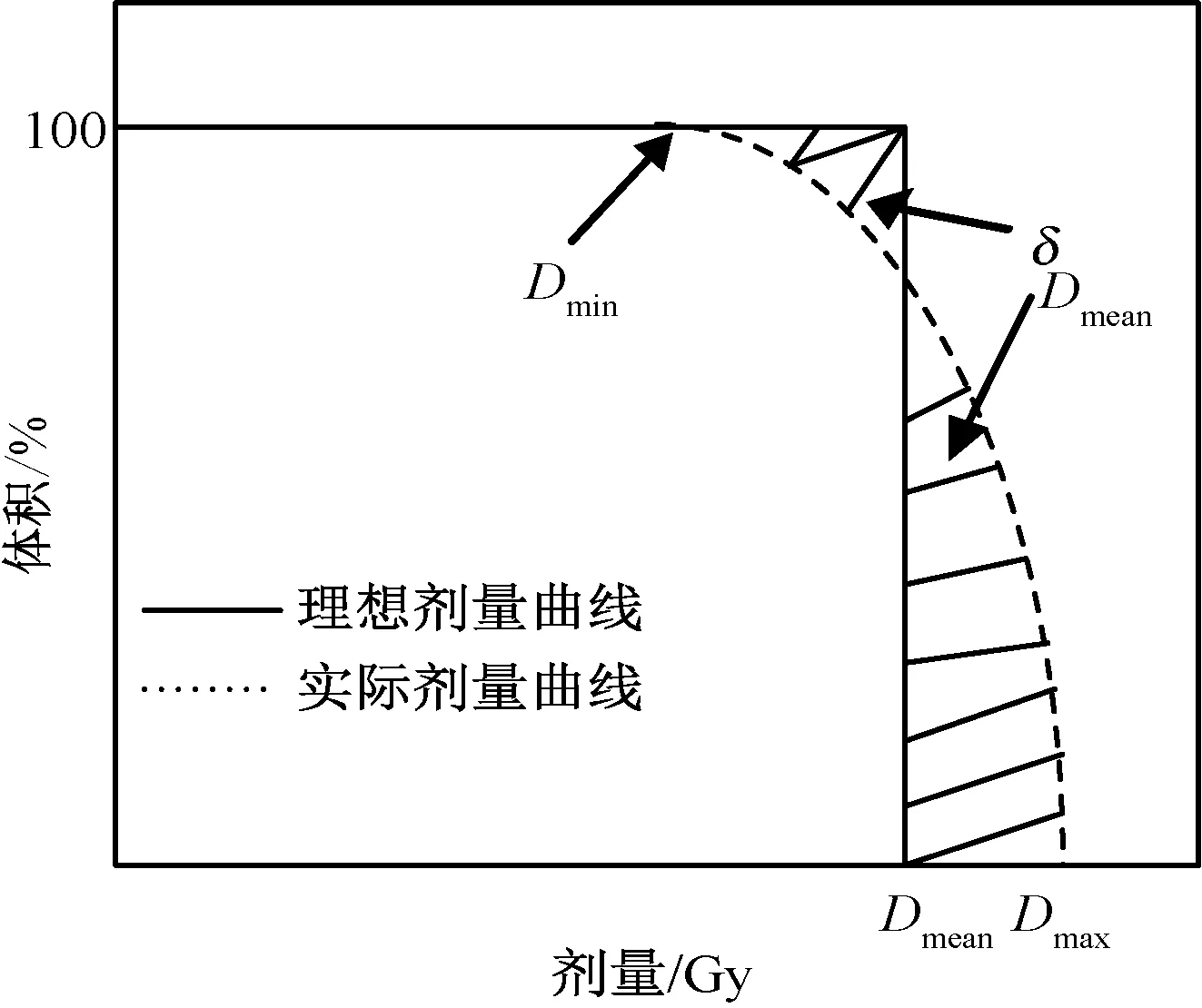
图4 平均剂量准则Fig.4 Mean dose criterion

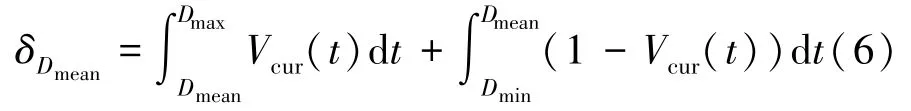
1.2.2 计划评估

图1 中矩形框区域I 步骤执行完后，开始评估当前计划。 采用式(7)和式(8)所示的评价函数分别对靶区和危及器官OAR 的剂量覆盖特性进行评估。

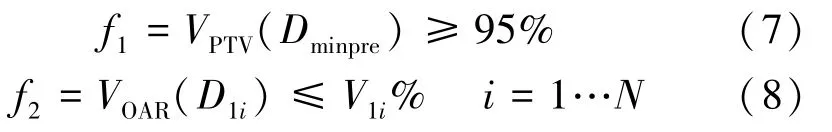
式中，N是OARs 剂量-体积(dose-volume，DV)约束的个数。 计划评估过程中执行如下准则:(1)如果靶区剂量满足条件，而有些危及器官DV 约束不满足，算法将在保证靶区处方剂量要求的前提下改善危及器官的DV 约束指标；如果在不损害PTV 剂量覆盖特性的前提下，危及器官的DV 约束不能都得到满足，则优先考虑危及器官的高剂量区域；(2)如果靶区的剂量未得到满足，则赋予控制靶区的子目标函数更大的惩罚，直到靶区的约束条件得到满足；(3)如果靶区和危及器官的剂量都得到满足，算法试图在保证危及器官DV 约束的基础上尽可能的改善靶区的剂量覆盖特性。

1.2.3 权重补偿阶段

通过引入补偿系数k，补偿阶段将赋予未满足约束的指标更高的惩罚，如式(9)所示，对于每一个病例，初始值k等于1。 然后重复执行图1 中矩形框I 中的迭代算法。k的表达式如式(10)所示，steplength 代表k值的迭代更新步长，取steplength ＝1，j表示补偿阶段的迭代次数。

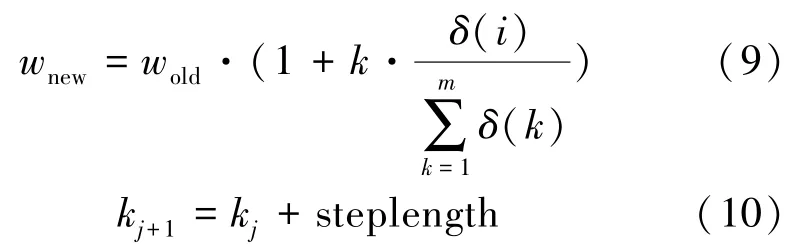
1.2.4 权重因子归一化

在自动优化过程中，为了避免数值误差，通过归一化将权重因子限定在(0，1)范围之内，如式(11)所示。 值得提出的是，从数学的角度来看，归一化不会影响最优解的质量。

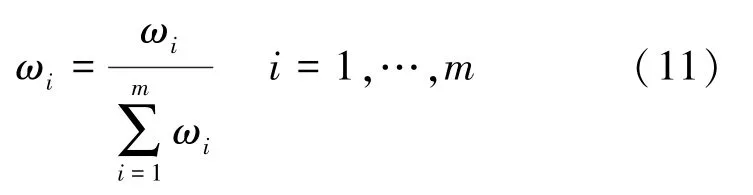
1.3 实验设定

所提出的权重因子自动优化方法在10 例前列腺癌病例上进行验证。 在本文所有实验中，患者采用仰卧位的方式模拟和治疗，器官的勾画方法、射线源类型和机架角度的设置同参考文献[3]中的方法。 在优化过程中考虑一个PTV 和两个危及器官(直肠和膀胱)，采用5 个共面6 MV 光子束射野( 36°、100°、180°、260° 和324° )照射。 物理优化总目标函数采用加权和的形式，靶区用处方最小剂量(Dmin＝74 Gy)[3]准则和处方平均剂量(Dmean＝78 Gy)[3]准则约束，各危及器官采用3 个最大DVH 约束，处方剂量如表1 所示。 值得注意的是，根据患者组织结构之间的差异，体积约束可以适当的收紧和放松。

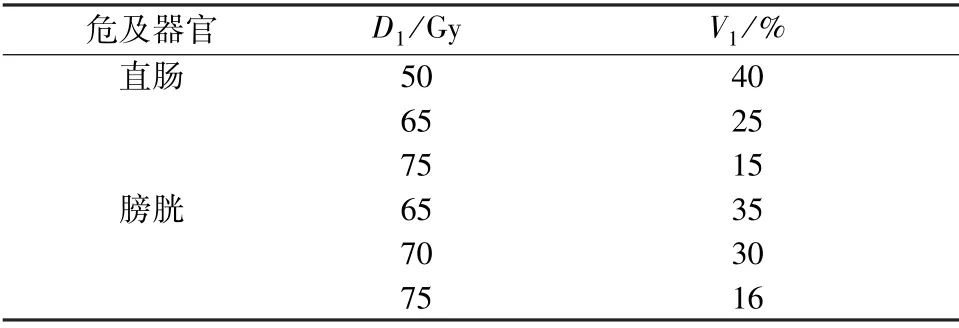
表1 DV 子目标函数的约束D1 和V1Tab.1 D1 and V1 for the DV sub-scores

靶区计划评价指标有式(12)所示的适形指数(conformity index，CI)[20]和式(13)所示的均匀性指数(homogeneity index， HI)[20]。 CI 用来描述靶区的均匀性，式中Vτ是靶区体积，Vτ，ref是靶区接受剂量大于等于参考剂量的体积，Vref是接受剂量不小于参考剂量的总体积，文中参考剂量取D95%的靶区剂量。 HI 用来衡量靶区的均匀程度，D5%和D95%分别表示靶区DVH 曲线上5%和95%体积接受到的剂量。

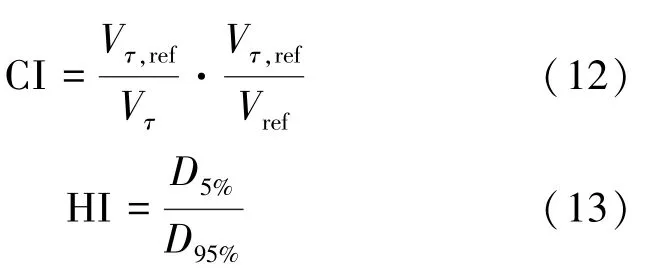
危及器官的剂量覆盖特性由Marks 等[21]提出的评价准则给出，如表2 所示。 同时，为了更好地保护危及器官，直肠和膀胱接受的最大剂量要求低于80 Gy[22]。 另外，通过与先前研究[23]所得同病例的人工计划进行比较，从剂量学(DVH 曲线、Dmin、Dmax和Dmean、Marks 评价准则)和生物学(gEUD、TCP，NTCP)两方面验证了权重因子自动优化方法的有效性。 人工计划与自动计划采用完全一样的实验平台、实验设定等，只是权重因子的调整方式不同，前者人工试误确定，后者采用本研究自动方法确定。

表2 直肠和膀胱的Marks 评价准则Tab.2 Marks criteria for bladder and rectum

10 例前列腺癌病例的实验数据采用了平均值加减标准差的统计形式，记为。 统计方法采用显著性水平等于0.05 的Wilcoxon 秩检验方法。

2 结果

2.1 补偿系数的影响

未通过计划评估的计划，为了实施进一步优化，通过引入补偿系数赋予未满足剂量目标更大力度的惩罚。 实验结果表明，在本研究的实验设置情况下，约束靶区的子目标函数权重因子需要引入额外的补偿系数。

以病例10 为例展示自动权重因子优化方法的进化过程如图5 所示。 由图可见，随着补偿系数的增加，即优化过程中赋予PTV 更大的惩罚，靶区的剂量覆盖特性变好，而对危及器官的保护性变差，这是由放疗的固有矛盾决定的。 补偿系数的引入可以增加算法的灵活性。

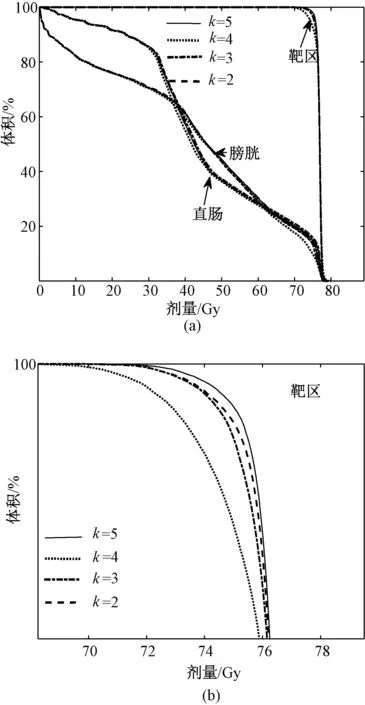
图5 自动优化进化过程(病例10)。 (a)整个DVH 曲线；(b) 靶区的高剂量覆盖特性Fig.5 Evolutionary process of the automation optimization(for patient 10).(a) Full DVH curves； (b) High dose region of PTV

2.2 计划比较

2.2.1 剂量学比较

1)DVH 曲线

10 个自动优化计划与人工优化计划的CI 和HI比较如表3 所示。 由表可见，提出的自动优化方法能产生较好或者相似的靶区剂量适形性和均匀性，但是CI 和HI 均无显著性差异(P＞0.05)。

表3 自动优化计划和人工优化计划的靶区CI 和HITab.3 Dose Conformity and Homogeneity to the PTV of the automatic plan and manual plan

图6 所示为自动计划和人工计划在病例9 上的DVH 曲线比较。 图中实线表示人工计划，虚线表示自动计划。 与人工计划相比，自动计划能够在保证靶区剂量覆盖特性的前提下，更好的保护危及器官。 与人工计划比较，自动计划中直肠和膀胱的平均剂量都有不同程度的降低，V65、V70和V75分别降低了5.05%、6.70%和7.57%。

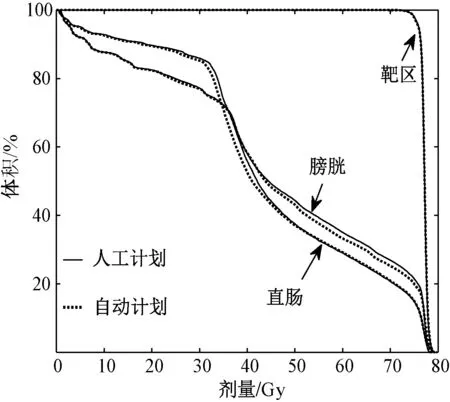
图6 病例9 上的DVH 计划比较Fig.6 Comparison of DVH plans for patient 9

为了进一步研究自动优化计划的实用性和有效性，将所提出的自动优化方法应用到另一种物理优化中。 另一种物理优化保持与第一种物理优化相同的实验设置，同样采用目标函数加权和的形式。 与第一种物理优化不同的是，危及器官采用处方最大剂量Dmax＝80 Gy 准则约束，靶区采用处方平均剂量Dmean＝78 Gy 准则约束。 图7 中的实线和虚线分别表示人工方法和自动方法为病例1 所做的计划，图中的max 表示基于最大剂量的物理优化。由图可见，自动方法能产生与人工计划相似的满足临床剂量要求的自动放疗计划。 需要指出的是，根据不同的临床要求，可以采用不同的准则约束靶区或者危及器官，比如，当对靶区内接受剂量大于D1的体积有大于V1要求时，可以对靶区采用最小DVH约束，本研究的自动优化方法同样适用。

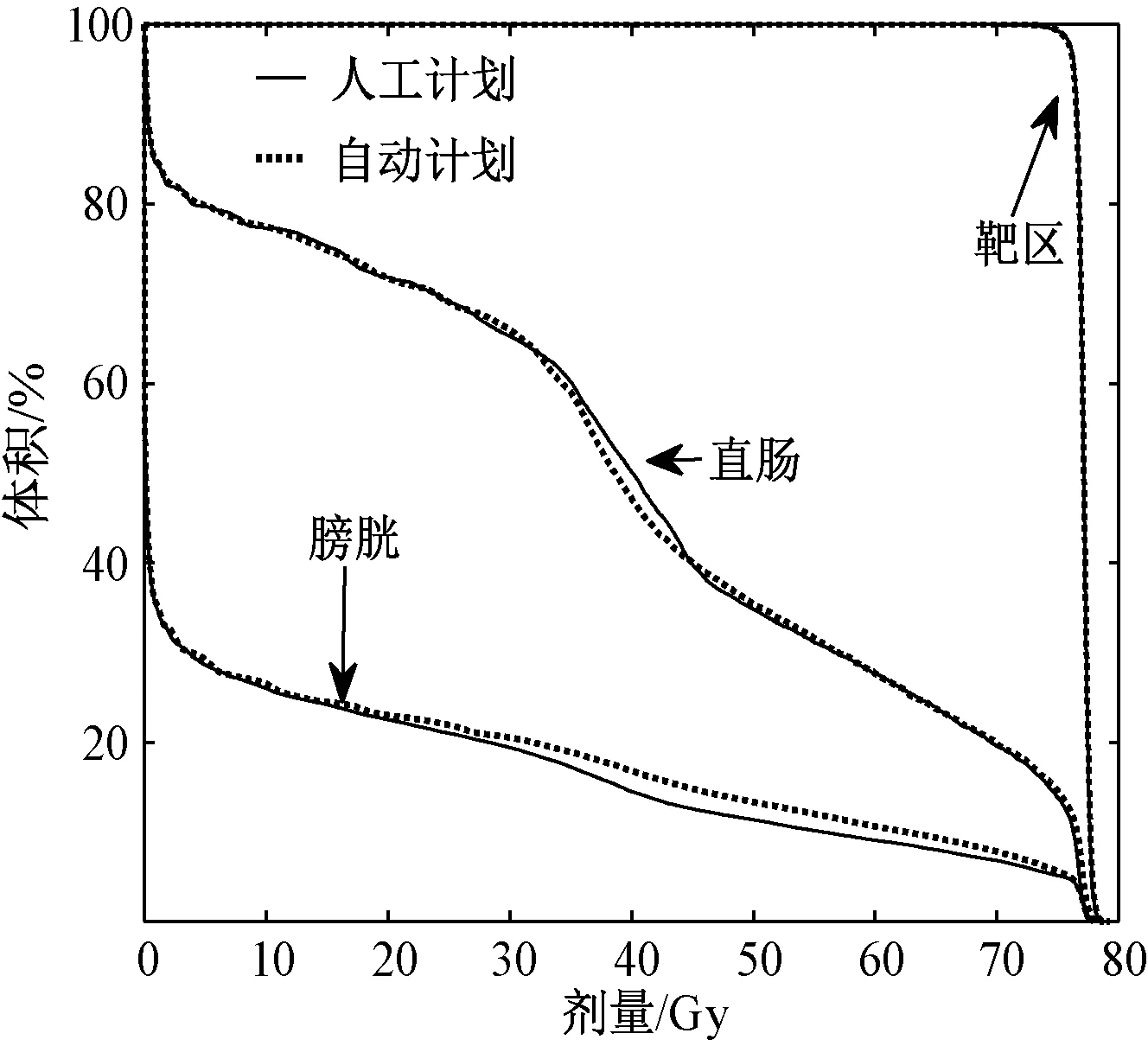
图7 病例1 上的max 计划比较Fig.7 Comparison of max plans for patient 1

2)Dmin、Dmax和Dmean

由表4 可知，采用文中提出的自动优化方法得到的自动计划与人工计划相比，靶区、膀胱和直肠的这些剂量特性均无显著性差异(P＞0.05)，能保证相似的靶区剂量覆盖特性和对危及器官的保护。

表4 自动优化与人工优化相比剂量统计评分比较( ±s)Tab.4 Comparison of the dose statistics score of automatic optimization compared with manual optimization( ±s)

表4 自动优化与人工优化相比剂量统计评分比较( ±s)Tab.4 Comparison of the dose statistics score of automatic optimization compared with manual optimization( ±s)

膀胱/Gy 靶区/Gy 直肠/Gy DminDmaxDmeanDminDmaxDmeanDminDmaxDmean自动优化73.22±1.86 79.90±0.51 77.14±0.10-78.71±0.5934.26±16.44-77.98±0.1648.24±3.01人工优化73.15±1.93 79.53±0.46 77.09±0.09-78.70±0.6634.79±17.36-78.52±0.2148.17±2.76

3)Marks 评价

Marks 临床实践指导评价准则如表2 所示，表5为2 种优化方法的对比结果。 从表5 可以看出，采用本研究提出的自动优化方法得到的计划与人工计划相比，除了膀胱V75有显著性差异(P＜0.05)外，其它指标均无显著性差异(P＞0.05)。

表5 自动优化与人工优化相比Marks 准则评价评分比较( ±s)Tab.5 Comparison of the Marks score of automatic optimization compared with manual optimization( ±s)

表5 自动优化与人工优化相比Marks 准则评价评分比较( ±s)Tab.5 Comparison of the Marks score of automatic optimization compared with manual optimization( ±s)

注 a 代表有显著性差异，即P＜0.05。Note a represents significant difference (P＜0.05).

优化方法直肠V65/%V70/%V75/%V50/%V65/%V75/%膀胱自动优化22.62±13.5618.85±11.3412.82±7.22a37.63±2.1124.55±1.0513.87±2.16人工优化23.70±13.8119.50±11.1811.96±6.0837.88±1.5624.96±0.9413.77±3.27

2.2.2 生物学比较

由表6 可知，采用文中提出的自动优化方法得到的自动计划与人工计划相比，靶区的TCP 和gEUD 危及器官膀胱的NTCP 和gEUD，直肠的NTCP 和gEUD 均无显著性差异(P＞0.05)。

表6 自动优化与人工优化相比生物指标评分比较( x- ±s)Tab.6 Comparison of the biological indices of automatic optimization compared with manual optimization ( x- ±s)

2.2.3 计划效率

在自动优化实验中，对于不同的前列腺癌病例，采用自动优化方法花费1-3 min 就可以生成满足临床要求的自动计划，而人工优化需要有经验的物理师花费1-3 h 才能生成临床可接受的人工计划，自动方法很大程度上提高了放疗计划效率。 而且，放疗优化目标函数中的子目标函数越多，算法的优势越明显。

2.3 初始权重因子的影响

上述实验中，采用了均匀的初始化权重因子，即(1/8， 1/8， 1/8， 1/8， 1/8， 1/8， 1/8， 1/8)。 还测试了多组不同的初始化权重因子对算法的影响。实验结果表明，不同的初始化权重因子不会明显地影响计划的质量。

3 讨论

本研究基于定积分理论提出了一种新颖有效的放疗权重因子自动优化方法。 自动优化方法避免了放疗物理师采用传统人工试误方法的繁琐工程，不仅减轻了物理师的工作量提高了放疗效率，而且有利于放疗的智能化实现。

首先，本研究对物理优化中的权重因子自动优化方法进行了主要研究，主要原因是物理准则应用灵活且具有明确的放射物理学意义[24]，基于物理准则的物理优化比生物优化更加直观[25]，被广泛应用与目前的商业放疗计划系统中。 同时，当前的生物准则和DVH 曲线没有直接的联系[25]，而基于定积分的放疗权重因子自动优化方法是根据当前计划劣于原始计划DVH 部分的面积差求出权重纠正因子，所以本研究方法不适用于生物优化。

其次，另一个值得探讨的问题是处方剂量对权重因子自动优化方法的影响。 一方面，优化过程中是否需要补偿阶段与处方剂量紧密相关，当处方剂量与实际能达到剂量的差异较小时，不需要补偿阶段的运行即可生成满意的计划；当处方剂量与实际能达到剂量的差异较大时，需要补偿阶段参与优化过程，并且处方剂量与实际能达到剂量的差异越大，补偿系数的作用越明显。 在本研究中采用的处方剂量只会导致不同的补偿系数k，不会导致计划质量的不同，具体表现在图1 矩形框II 中的优化步骤执行次数增加。 另一方面，当在给定处方剂量情况下，经过多次自动优化过程得不到满意计划时，需要人工修改处方剂量后，再进行权重因子的自动优化。 这主要归因于相比于权重因子，处方剂量与临床紧密相关[26]，有时调整处方剂量比调整权重因子更有效，不同的处方剂量会导致不同剂量分布结论一致[18，27]。

再次，文中采用两种物理优化测试了权重因子自动优化方法的有效性。 第一种物理优化中，靶区采用最小剂量准则和平均剂量准则约束，每个危及器官采用3 个最大DVH 准则约束；第二种物理优化中，靶区采用平均剂量准则约束，危及器官采用最大剂量准则约束。 需要指出的是，放射治疗过程中涉及多个组织结构，每个组织结构上均至少需要一个约束准则来控制该结构上的剂量分布。 然而，评价一个治疗计划的优劣程度，通常是评价优化所得的剂量分布是否满足相应的评价准则。 因此，在放射治疗优化的过程中，一般使用评价准则的约束函数构成加权和的总目标函数，以更准确地控制和评价对应组织上的剂量分布[28]。

另外，与引言中提到的其他自动优化算法相比，本算法不需要参考计划[7-13]、大量的临床数据训练模型[14-17]、和设计复杂的隶属度函数[18]。 由于本算法与其他自动权重因子优化算法的本质差异，文中未对基于定积分的权重因子自动优化算法与其他自动优化算法进行比较。

相比与其它自动优化方法，提出的自动方法虽然有文中描述的优点，然而仍然有改进的空间。 一是，补偿系数的更新方式是启发式的，需要一种调整k的高效方法；二是，只研究了权重因子的自动优化，需要将处方剂量的自动优化纳入优化过程，实现真正的全自动优化。 尽管有这些不足，该自动优化方法能生成临床可接受的计划，可作为具体计划的参考计划和计划的起点，或者提供了计划的最低质量[29]。

4 结论

基于定积分理论，本研究为IMRT 逆向物理优化提出了一种简单易行的自动迭代调整目标函数权重因子的方法。 通过与同病例的人工计划相比，在10 例前列腺癌病例上验证了新方法的有效性。根据提出的权重因子调整策略自动迭代调整权重因子，直到生成满意的放疗计划。 与人工计划相比，自动计划具有相当的或者较好的靶区覆盖特性和对危及器官的保护，并且提高了优化效率。

(致谢:在此衷心感谢张麟华等在本研究工作中给予的帮助)