开卸压槽防治岩爆的数值模拟研究
2022-10-19韩月欢刘溪鸽朱万成
韩月欢,刘溪鸽,朱万成
(东北大学资源与土木工程学院,辽宁 沈阳 110819)
在深部岩石工程中,工程岩体在高地应力下积蓄了大量的应变能,随着开挖、爆破等工程扰动,围岩应变能急剧释放,易诱发岩爆灾害[1]。岩爆具有很强的突发性、随机性和危害性,可造成开挖工作面的严重破坏、设备损坏和人员伤亡,已成为岩石地下工程和岩石力学领域的世界性难题。
开槽卸压或是主动降低围岩高地应力、防治岩爆的有效措施之一,即在巷道刚开挖后用高压水枪[2]、破碎孔爆破或聚能预裂爆破[3]的方法在壁面上切割出一个或多个卸压槽,使得应力向围岩内部转移,从而达到降低围岩应力、预防岩爆的目的。开槽卸压方法为巷道环向应变提供了空间,将围岩的径向挤压变形转化为环向变形,并消耗掉一部分的环向变形,降低巷道壁的环向应力[3],进而大大降低岩爆风险。与此同时,巷道帮壁开槽后,根部将形成塑性区,消耗了围岩中的部分弹性应变能,卸压槽口围岩破碎压密后也会消耗部分弹性应变能。
关于开槽卸压的研究,秦跃平等[2]研究了利用高压水枪开槽并指出防治效果主要取决于卸压槽的深度和宽度;罗忆等[3]采用FLAC数值模拟计算,得出开槽为环向应变提供变形空间,使得围岩环向应力减小,并指出,合理布置卸压槽的部位、间距及数量可以提高防治的效果;黄运飞等[4]以天生桥引水隧洞为工程背景,证明了开槽卸压对岩爆具有明显的防治效果;刘允芳等[5]研究了较窄的卸压槽对降低局部应力的效果。随着岩石工程逐渐向深部发展,垂直应力和水平应力趋于相等,此时开槽卸压与其他卸压方法相比效果较好,且施工难度低、工程量小[6-8]。
目前,关于开槽卸压防治岩爆方案缺乏现场应用,一方面受限于开槽卸压设备的缺乏和施工传统的制约,另一方面则在于缺乏室内实验验证和相关理论支撑。此外,由于卸压槽的宽度和深度对卸压效果的影响较大,对于卸压槽的位置和形状要求较高[3],现场施工难度较大。因此,如何根据地应力条件和围岩稳固性正确选择合适的开槽方式、开槽位置、开槽数量以及支护方式等参数仍需进一步探讨。本文利用离散元PFC2D软件数值模拟,结合室内实验结果,研究在不同地应力状态下卸压槽位置、数量等对卸压效果的影响,并分析卸压槽对岩爆的防治效果。
1 模型改进与参数标定
本文研究主要基于颗粒流程序PFC2D软件开展,其基本组成是颗粒和接触,颗粒和接触的几何和力学性能决定了模型的宏观力学性能。但是,在利用PFC2D内嵌的平行黏结模型(PBM)模拟时,由于圆形颗粒之间的互锁作用较低[9],颗粒旋转的阻力较弱,加载过程中颗粒会产生过度旋转,导致岩石的抗拉强度偏高,造成不符合真实岩石的低压拉比情况(UCS/T)[10-11]。针对上述问题,本文采用了基于矿物组成与分布的柔性簇(Cluster)模型和基于断裂损伤的岩石劣化机理对模型进行改进。
1.1 矿物组成与分布
本文以花岗岩为实验和模拟研究对象。通过矿物学分析可知,花岗岩的主要成分为长石、石英和云母,且各矿物组分占比大约为55%、40%和5%[12]。由于不同矿物成分抵御变形破坏的刚度和强度不同,在复杂应力条件下会出现变形不协调的现象,导致微裂缝往往在不同矿物的连接处最先出现。基于该假设,本文对花岗岩图像进行灰度处理,得到花岗岩的矿物构成及分布,进而在PFC2D软件中构建出与真实花岗岩矿物组成与分布相同的数值计算模型(图1),然后对不同矿物赋予不同的强度和刚度参数,相同矿物之间即形成团簇(Cluster),以此提高颗粒之间的互锁作用,实现对颗粒旋转的有效抑制。
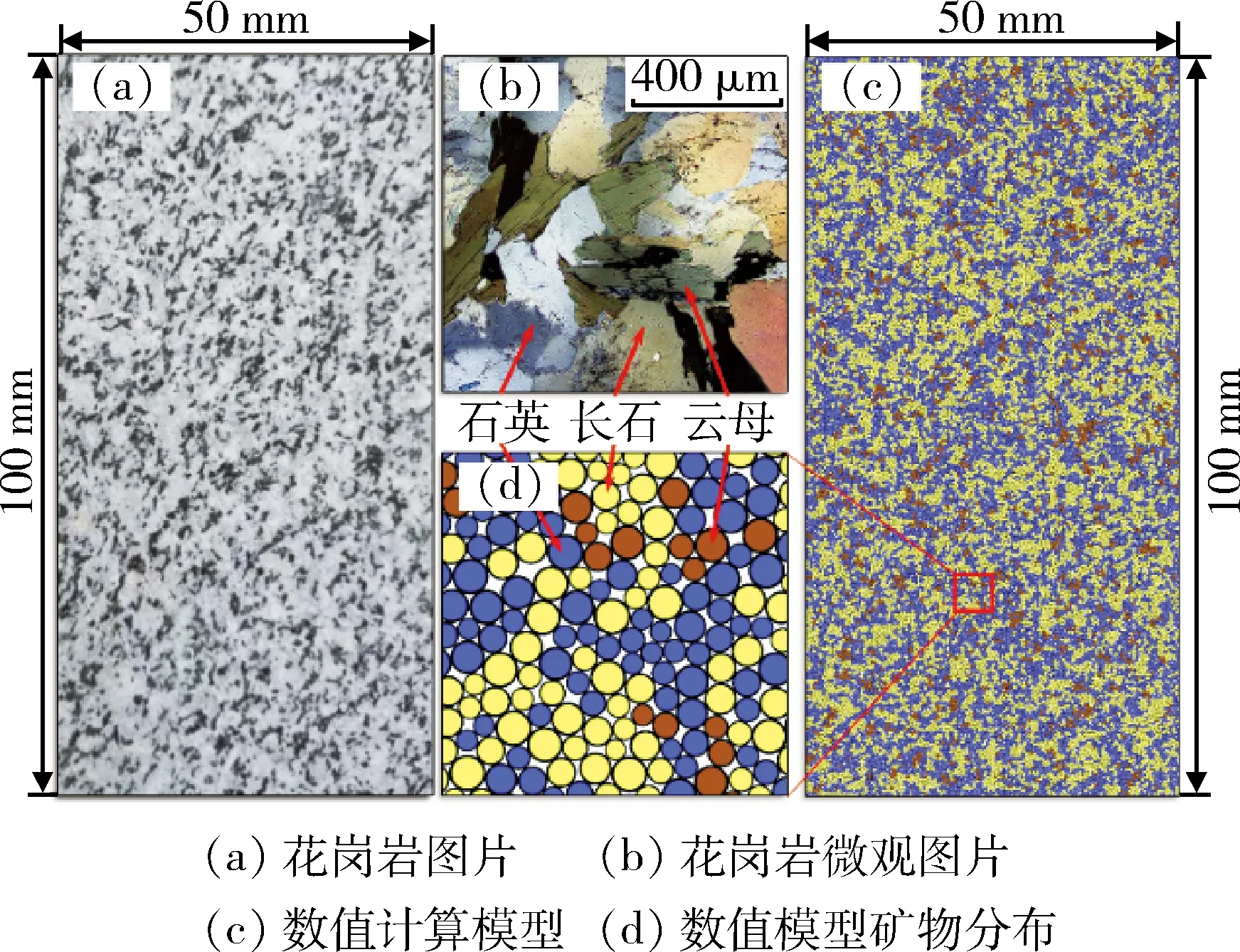
图1 真实花岗岩与数值计算模型的宏观与微观对比
1.2 岩石劣化机理
断裂力学观点认为,岩石微裂纹的损伤效应是由于局部应力集中而起裂产生微裂纹,岩石的自由表面增加,从而降低了岩石结构传递荷载的能力和比例,进而产生的强度恶化现象[13]。在利用PFC2D软件模拟时,颗粒间平行黏结接触的断裂有效模拟了微裂纹的产生,但由于颗粒流数值模拟采用圆形颗粒,颗粒间极易组成三角形结构(图2(b)),使得相邻颗粒之间接触的偏转角一般在60°左右,且随着颗粒大小的差异性增大,微裂纹偏转角的差异性也增大,而实际岩体中微裂纹一般沿直线扩展,即偏转角度要小很多,只有在极特别情况下才会出现较大的偏转角度。
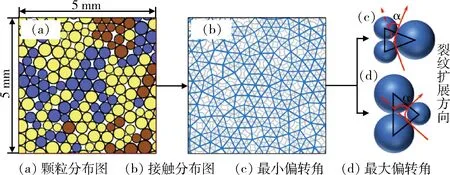
图2 PFC软件中颗粒接触结构及裂纹扩展方向
因此,在PFC模拟过程中微裂纹的偏转角度与实际岩体中的偏转角度相差较大,导致模拟过程中裂纹扩展方向紊乱,裂纹无法有效贯穿实现试样破坏,进而导致破裂接触增多以及主裂纹不显著。针对这一问题,有必要在一定偏转角范围内搜索接触并对其进行弱化,引导正确的裂纹扩展方向。具体地,基于宏观裂纹尖端往往存在一定范围的损伤区这一物理事实,本文针对PFC2D软件颗粒流程序提出了裂纹扩展劣化算法:当平行黏结接触断裂时,在接触的法向方向一定区域内(由α、r控制,图3(a))扫描所有有效黏结接触,并选取夹角最小的接触进行劣化,选取的接触距离断裂接触的距离越近,其劣化的程度越大,反之越小,劣化系数服从指数函数(式(1))。
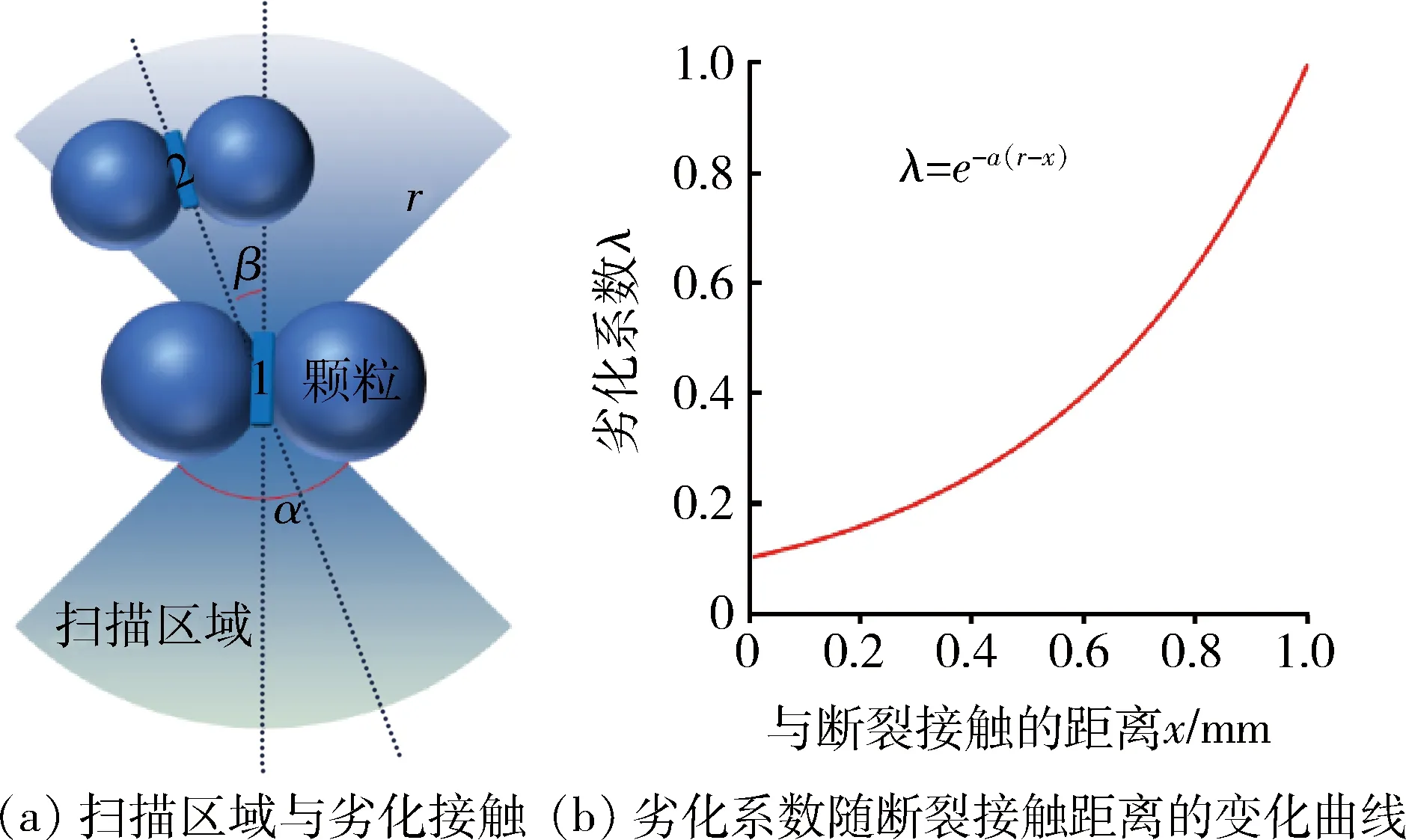
1-断裂接触;2-弱化接触;α-扫描角度;r-最大扫描半径;β-所有接触最小的偏转角度;λ-劣化系数;a-调节系数
λ=e-a(r-x)
(1)
式中:a为调节系数;r为最大扫描半径,mm;x为断裂接触与劣化接触之间的距离,mm。
在本文研究中,a取2.3×103,r取1 mm,等于2~3个颗粒直径,α取60°,其弱化曲线如图3(b)所示。
1.3 模型参数标定
在利用离散单元法模拟时,岩石模型的宏观力学性质由颗粒和接触的微观力学参数决定,需要基于物理实验进行标定,由于细观参数与宏观力学参数之间没有直接的数学关系,需要利用试错法不断调整模型的细观参数得到与现实花岗岩试样相近的宏观力学参数,以期能够很好地反映真实岩石的力学性质,本文研究最终确定的细观参数见表1。
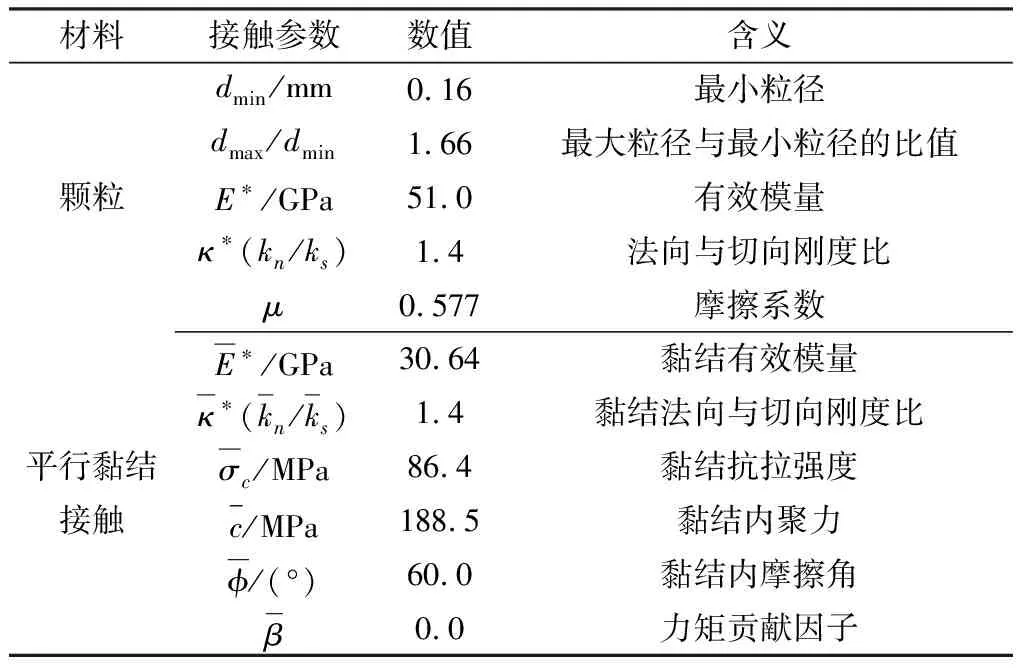
表1 标定的平行黏结模型细观参数
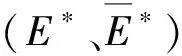
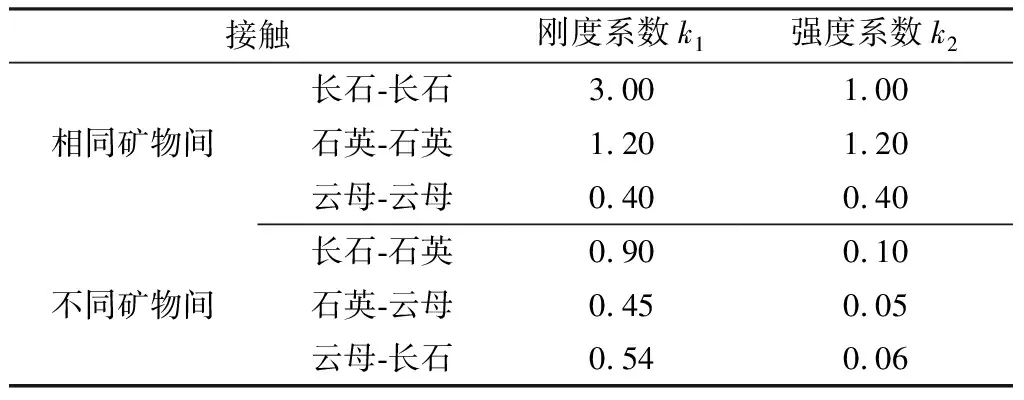
表2 不同矿物之间接触的刚度系数和强度系数
引入的柔性簇(Cluster)模型与岩石劣化机理有效地弥补了平行黏结模型的不足,使其更接近真实岩石的强度参数,在此基础上标定好的模型宏观力学参数见表3,其力学参数与真实花岗岩的力学参数趋于一致,可以较好地反映真实花岗岩的力学性质与破坏特征。

表3 花岗岩的实验和数值模拟宏观力学参数
2 预制裂缝加载试验
地下巷道两帮围岩受力情况如图4(a)所示。在不考虑塑性区的情况下,巷道的环向应力和剪应力越靠近巷道壁越高,呈现出非均布力的状态,在这种状态下的围岩极易产生岩爆灾害。如果在巷道壁开槽,卸压槽为巷道环向应变提供了空间,围岩积累的应变能得以释放,环向高应力向围岩内部转移。与此同时,卸压槽有效防止了贯通裂纹的发展[14],从而大大降低了岩爆的发生风险。为了更加有效地验证数值模型的可靠性,本文研究进行了预制裂缝室内加载试验及其数值模拟,为了更加真实地模拟巷道两帮围岩的受力状态,特设立了如图4(b)所示的实验装置,在试样右侧施加固定位移约束模拟内部围岩径向应力,左侧模拟巷道壁的临空面并布置预制裂缝。在试样的顶部与加载板之间增加一个线性梯度厚度的钢垫板,即左侧比右侧厚,以此实现花岗岩试样上部的非均布力加载,模拟真实围岩中环向应力的非均布情况(在不考虑塑性区的情况下,巷道壁附近的环向应力一般高于围岩的环向应力),且可通过改变钢垫板的梯度情况调整上部加载力的非均布程度。具体试验过程如下所述。
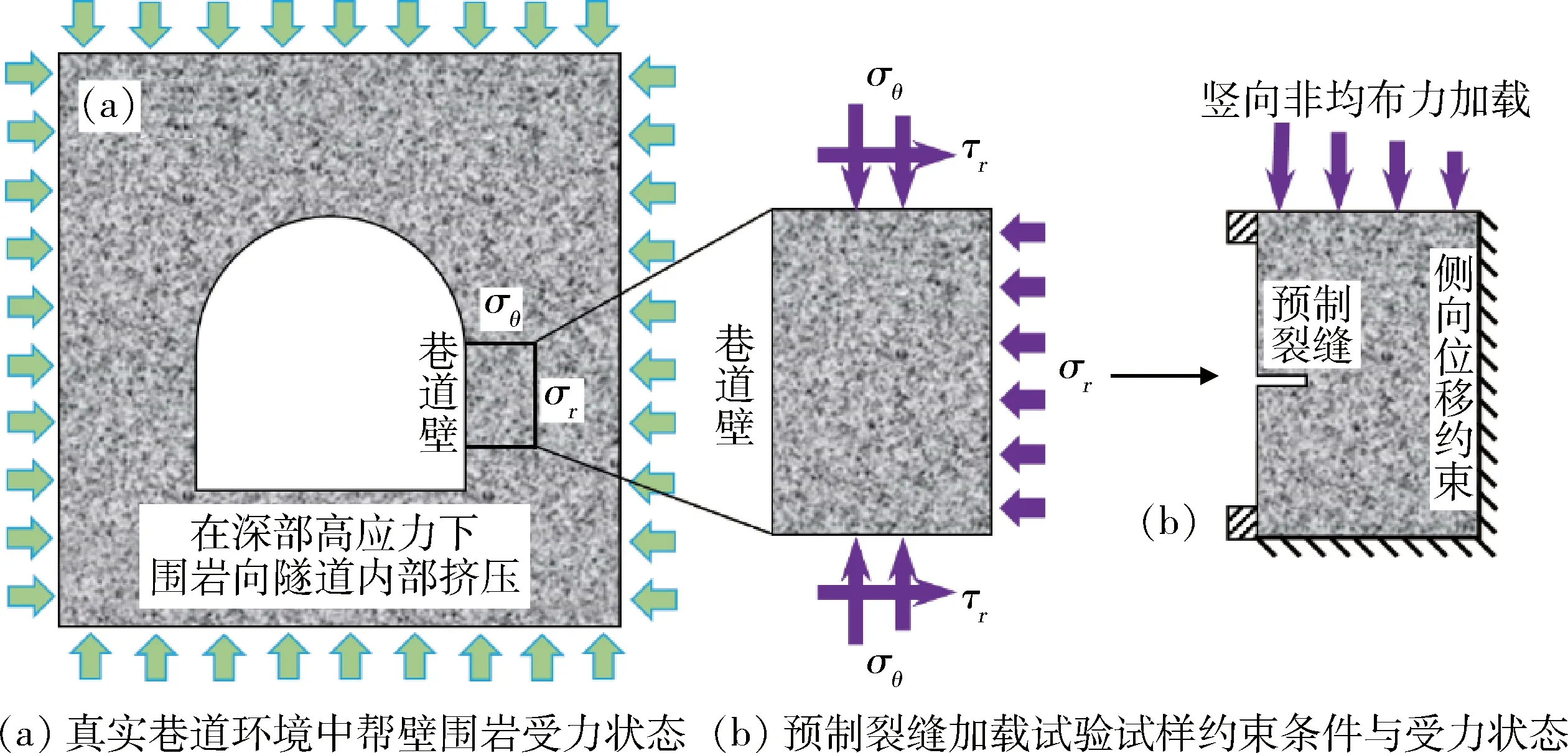
图4 深部高应力条件下巷道两帮围岩受力示意图及加载装置示意图
①采用150 mm×100 mm×50 mm(高×宽×厚)的花岗岩试样,在一定的偏载情况下,通过伺服单轴压缩试验机按照0.5 kN/s的力梯度分别对完整花岗岩试样和含有预制槽缝的花岗岩试样进行加载,卸压槽长度为3 cm,宽度为0.5 mm,监测并记录试验机的加载力和位移,同时采用常规录像和高速摄影的方法记录其在加载过程中的破坏模式。
②利用离散元数值模拟软件PFC2D建立与物理实验尺寸相同的数值模型并对其进行加载,调整加载板角度,使得加载过程中的应力应变及破坏模式与物理试验吻合,此时可认为模拟的非均布加载力与物理实验的非均布加载力相同。
③利用步骤②确定的加载板角度对含有预制槽缝的数值模型进行加载,同样,卸压槽长度为3 cm,宽度为0.5 mm,记录应力应变及破坏模式,并可同时检测加载过程中模型的位移场、速度场和能量变化。
试验及模拟结果如图5所示,数值模拟与物理试验的破坏情况匹配良好,说明该数值模型及相关参数可用于模拟卸压槽对岩爆的弱化作用。

图5 预制裂缝室内加载试验及数值模拟结果对比
3 数值模拟及结果分析
3.1 模型构建
本文研究模拟的工况是三心拱巷道,模型尺寸如图6所示。由于实际岩体中存在复杂的节理裂隙等地质弱面,实际岩体的强度远远小于室内岩石试样的强度,因此模型参数需要进行相应的折减。
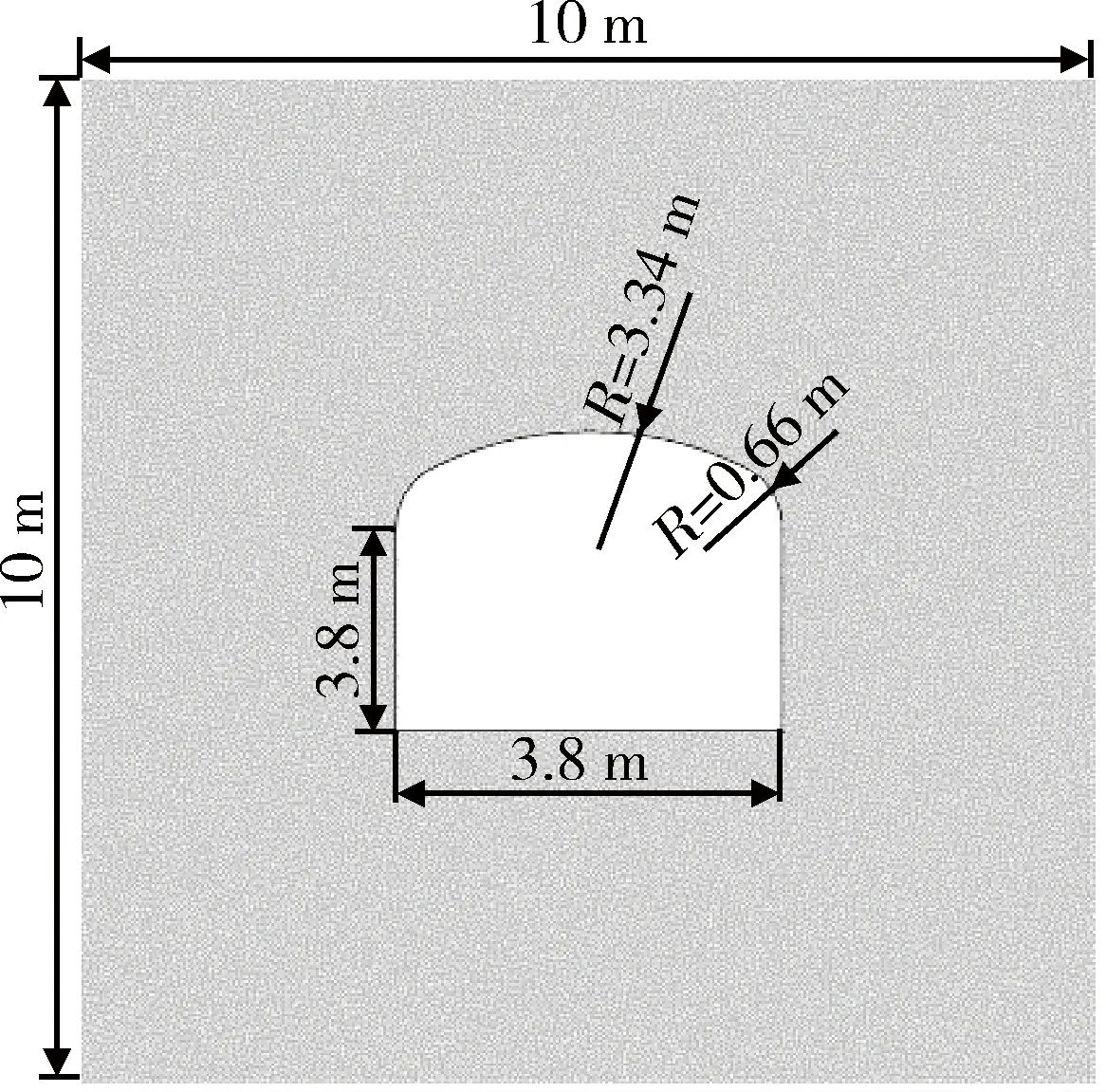
图6 巷道模型
由Hoek-Brown岩体破坏准则经验方程[15]进行计算,见式(2)。
(2)
式中:σ1为破坏时的最大主应力;σ3为作用在岩石试样上的最小主应力;σc为岩块的单轴抗压强度;m、s为与岩性及结构面情况有关的常数,可通过式(3)和式(4)估算[16]。
(3)
(4)
式中:mi为常数;RMR为受岩石强度、RQD值、节理裂隙以及地下水影响的岩体综合评价指标,由岩石力学分类表(RMR)[17]中对应的各项指标评分求和得出。
由于本文研究主要针对深部工程中的岩爆问题,岩体条件为质量较好的花岗岩岩体,故m取12.5,s取0.1。令σ3=0,可得岩体的单轴抗压强度σmc,见式(5)。
(5)
3.2 应力分析
侧压力系数λ=1.0,垂直应力分别为25 MPa、50 MPa时巷道不同开槽方式围岩应力分布如图7所示,应力以应力十字架方式展现,分别表示最大主应力方向和最小主应力方向。由图7可知,在巷道开挖后,主应力方向为环向应力,巷道围岩存在强烈的环向挤压,进而容易诱发岩爆。在侧压力系数λ=1.0时,除巷道拐角处存在应力集中外,巷道两帮应力较高,即巷道两帮对维持巷道稳定、承受围岩高应力起重要作用。
垂直应力为25 MPa,侧压力系数λ=1.5、λ=2.0时巷道不同开槽方式围岩应力分布如图8所示。对比图7和图8可知,随着侧压力系数的增大,主应力方向仍为环向应力,但巷道顶板和底板的应力增大,承载围岩压力的作用增加,尤其在侧压力系数λ=2.0时,巷道顶板和底板的应力已超过巷道两帮的应力,对维持巷道稳定、承受围岩高应力起着重要作用。
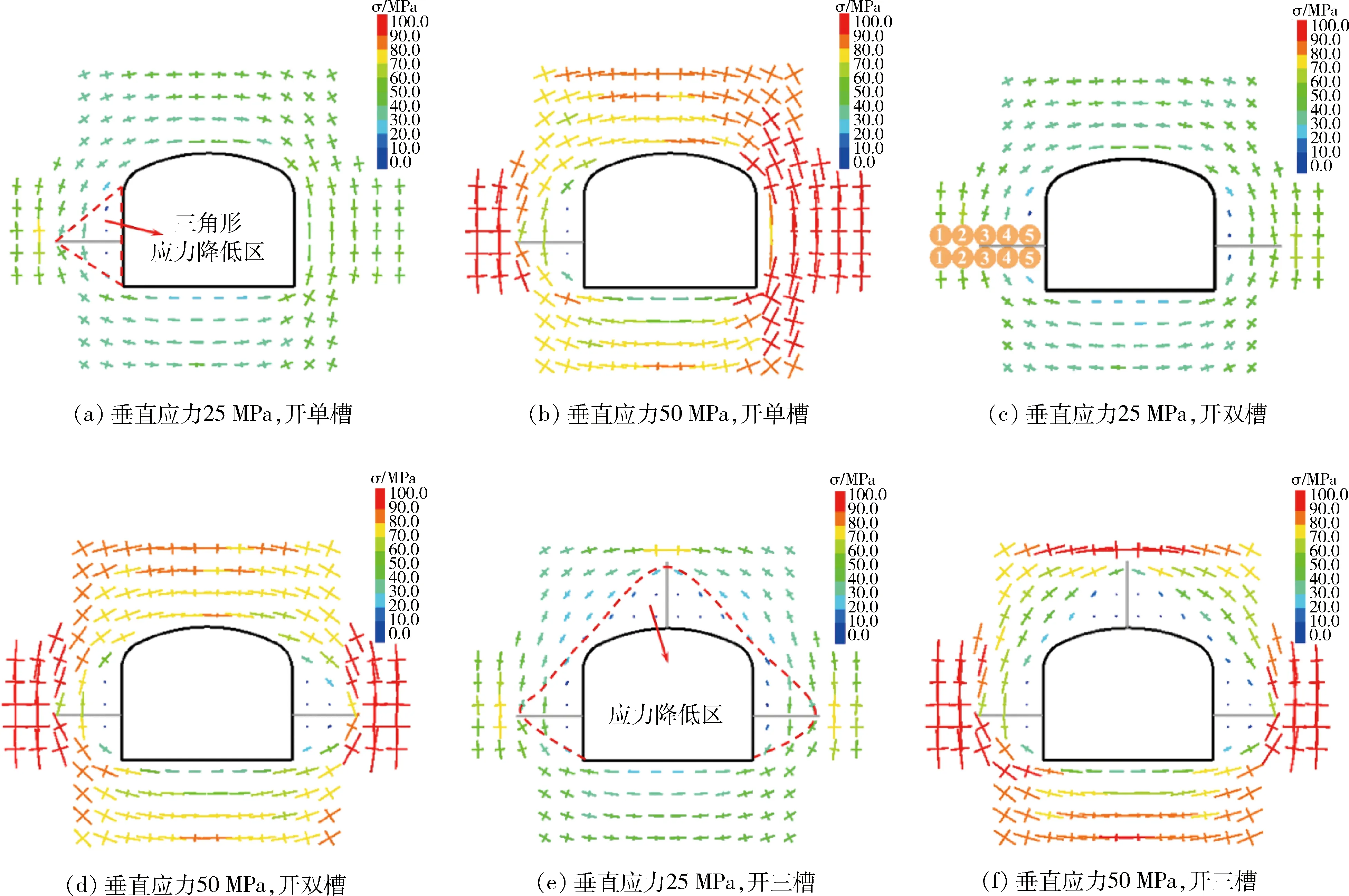
图7 侧压力系数λ=1.0时,不同垂直应力下巷道围岩不同开槽方式应力分布
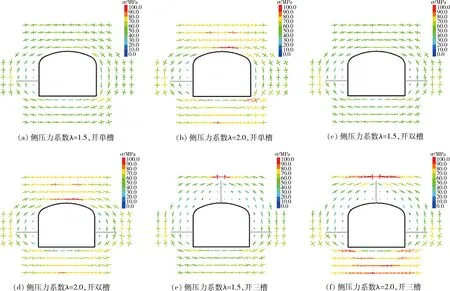
图8 垂直应力为25 MPa时,不同侧压力系数下巷道围岩不同开槽方式应力分布
综合图7和图8可以看出,卸压槽周围的应力显著降低,且距离巷道壁越近应力降低范围越大,降低程度越明显,形成大致呈三角形的应力降低区(图7(a)),使得围岩之前积累的应变能在应力降低区内快速释放,高应力向卸压槽底部转移,卸压效果明显;尤其是随着卸压槽数量的增加,巷道周围形成围绕巷道一圈的应力降低区(图7(e)),极大地改善了巷道围岩的应力状态,对于岩爆的防治有着较好的效果。
如图7(c)所示,在卸压槽上下两端各布置五个测量圆,以计算圆内的平均应力,测量圆半径为0.25 m,不同开槽方式下卸压槽周围测点的应力分布如图9所示。由图9可知,在距离巷道壁0.5 m内应力降低最为明显,且越接近临空面应力越小;在距离巷道壁0.5~1.5 m处相较于未开槽时应力有所降低但降低幅度不大,应力趋于稳定,随开槽深度的增加应力变化较弱;在距离巷道壁1.5~2.0 m处为卸压槽的底部,由于开槽的原因,应力集中转移到卸压槽底部,此处应力集中严重,应力甚至高于未开槽时的围岩应力;距离巷道壁超过2.0 m后,应力逐渐降低,趋向于围岩应力。
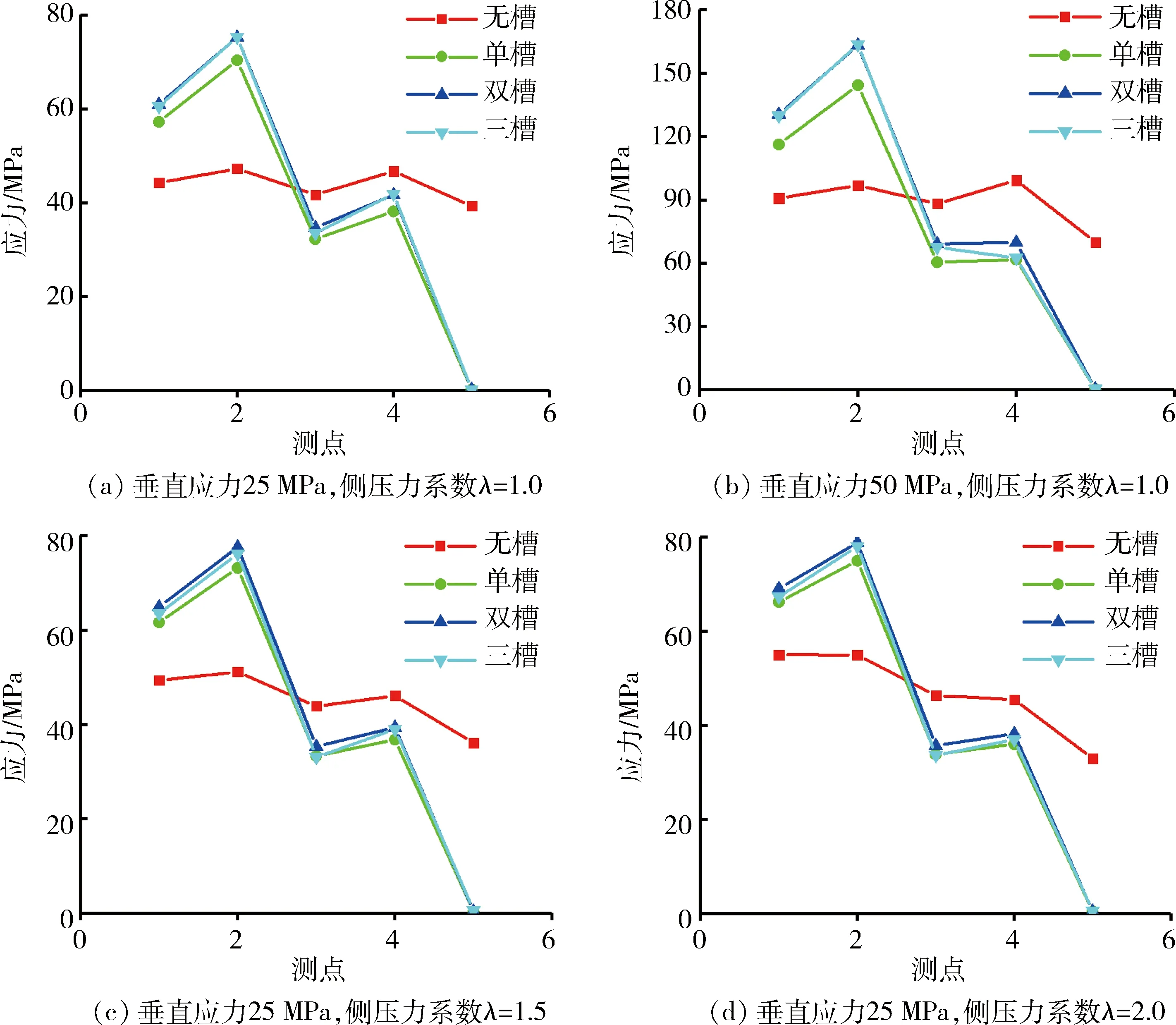
图9 不同垂直应力和侧压力系数下的应力分布
此外,对比三种开槽方式下卸压槽附近应力还可以发现,卸压槽对应力降低区内围岩的卸压效果会受到巷道中其他部位卸压槽的影响,所以在地应力不是很高的巷道中可采用局部开槽,只对应力集中区域进行开槽卸压,即可达到较好的卸压效果。
3.3 速度场分析
巷道应力集中过大时,贸然开槽可能会诱发岩爆。垂直应力25 MPa、侧压力系数λ=2.0时,水平应力较高;垂直应力50 MPa、侧压力系数λ=1.0时,水平应力、垂直应力均较高(图10)。由图10可知,在高地应力巷道中,开槽会破坏原有的微弱平衡状态、破坏围岩的稳定性,进而造成局部围岩破裂、岩块弹射,产生岩爆灾害。所以在地应力较高地区(≥50 MPa),单独采用开槽卸压并不能较好地防治岩爆灾害,需同时辅以相应的围岩支护方式以保持岩体完整、控制岩块弹射。
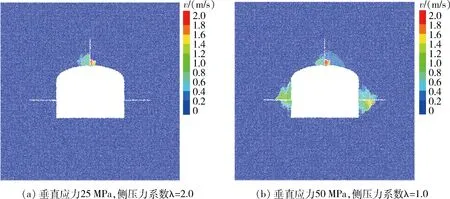
图10 不同地应力条件下开卸压槽后围岩的速度场
3.4 黏结破坏能分析
黏结破坏能(bond strain energy)[18]是平行黏结接触在发生拉伸或剪切破裂时所积累的应变能,其计算公式见式(6)。
(6)
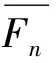
不同地应力条件下开卸压槽后的黏结破坏能如图11所示。由图11可知,随着开槽深度的增加,释放的黏结破坏能也相应增加,且增加幅度大致相同。
对比图11(a)和图11(b)可知,在侧压力系数相同(λ=1.0)的情况下,地应力越高,其开槽释放的黏结应变能就越大,且随着卸压槽数量的增加,黏结应变能也等比例增加,即每个卸压槽所释放的黏结应变能近似相等。
对比图11(a)、图11(c)和图11(d)可知,在垂直应力相同(25 MPa)的情况下,随着侧压力系数的增加,卸压槽释放的黏结应变能也会增加。但随着侧压力系数的增加,围岩的水平应力也逐渐增加,巷道顶板上开槽所释放的黏结应变能也随之增加。由图11(c)和图11(d)可知,开三个卸压槽释放的黏结应变能远远高于一个卸压槽和两个卸压槽,即巷道顶板上开槽所释放的黏结应变能远远高于巷道两帮开槽所释放的黏结应变能。故在侧压力系数较大时,在巷道顶板开槽能量的释放效果要优于巷道侧帮开槽。
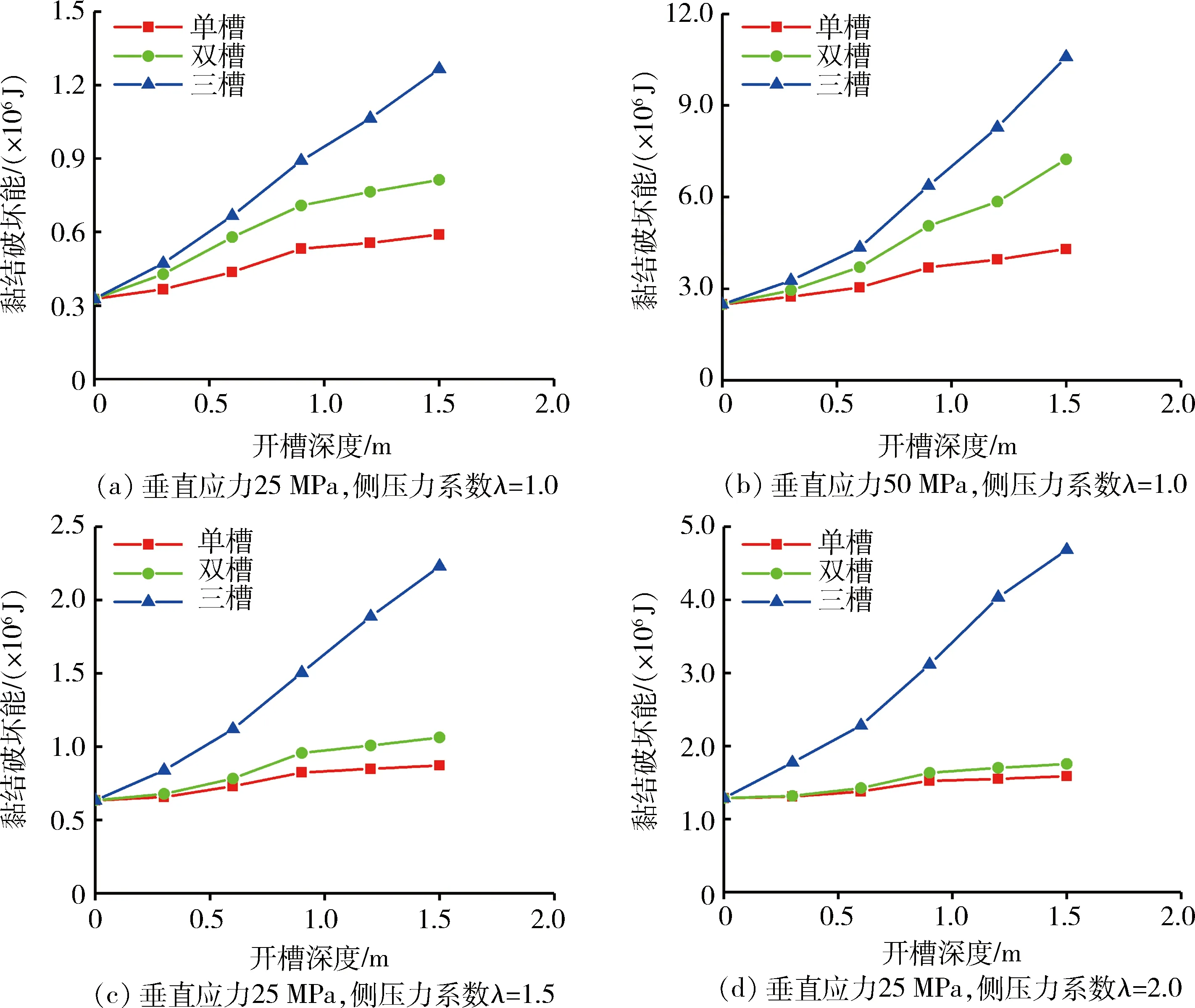
图11 不同垂直应力和侧压力系数下开槽的黏结破坏能
4 结 论
本文利用离散元数值模拟软件PFC2D,针对巷道模型开展了不同条件下的开槽卸压数值模拟研究,并分别探究了卸压槽数量、位置及不同地应力状态对卸压效果的影响,得到以下主要结论。
1)卸压槽周围会形成三角形的应力降低区,该区域内围岩积累的应变能会随着开槽的进行急剧释放,应力集中区朝卸压槽底部转移。
2)卸压槽对应力降低区内围岩的卸压效果会受到巷道中其他部位卸压槽的影响,在地应力不是很高的巷道中可只对应力集中区域进行局部开槽卸压,即可达到较好的卸压效果。
3)在地应力较高时(≥50 MPa),巷道围岩应力集中显著、能量积累过高,开槽卸压反而易造成局部围岩破碎、诱发岩爆,在这种情况下需同时辅以适当的围岩支护方案以保持围岩稳定。
4)在水平侧压力系数较小时,不同位置开槽所释放的能量十分接近;在水平侧压力系数较大时,巷道顶板开槽释放的能量要远高于在巷道侧帮开槽,即在水平侧压力系数较大时,在巷道顶板处开槽能量释放效果要优于巷道侧帮开槽。
