悬臂梁式电子秤全周倾斜称重技术研究*
2022-10-19王建乐裘国华李
王建乐裘国华李 青
(中国计量大学机电工程学院,浙江 杭州 310018)
电子秤称重作为现代质量计量的常用方法,其在金融贸易、生产制造、工业加工、科学研究等各种领域中有着广泛的应用,因此电子秤的准确性就显得尤为重要。
现阶段市场上,悬臂梁式的电子秤是使用最多、用途最广的电子秤。悬臂梁式电子秤在使用过程中安装位置的水平是保证其准确性的前提,但在实际应用当中,被安装平面常常是非水平的,例如车载的电子秤、运输带上的电子秤等等。这使得电子秤准确性降低,造成称重不准确甚至出现误差很大的现象[1-2]。
对于悬臂梁式电子秤因倾斜而产生误差的补偿,现阶段国内外研究不充分,相关文献较少,并且一般都只对单一方向上的倾斜误差进行补偿,如文献[3]。并且未有具体的补偿算法建模分析,实用价值低。同时对于电子秤的全周倾斜称重都没有说明[4-6]。
为此本文针对悬臂梁式电子秤的全周倾斜称重进行研究说明,并建立电子秤全周倾斜称重误差补偿数学模型。结合加速度传感器得到电子秤的姿态,通过测量的姿态和称重结果分析,根据实际优化模型,确定参数组,得到有效的补偿算法。经过实验检验,算法能有效地对悬臂梁式电子秤全周倾斜称重进行自动补偿,且满足国家标准《GB/T 7722-2005电子台案秤》规定对台案秤受倾斜引起的变化量指标[7-8]。
1 悬臂梁式电子秤全周倾斜称重影响
1.1 悬臂梁式称重传感器原理
悬臂梁式称重传感器核心部分为悬臂梁和应变电桥。悬臂梁一端固定,另一端受到重物由于重力而对悬臂梁产生的压力。应变片作为应变电桥的桥臂,粘贴在悬臂梁上,如图1(a)所示,图中黑色部分为应变片,灰色部分为悬臂梁。
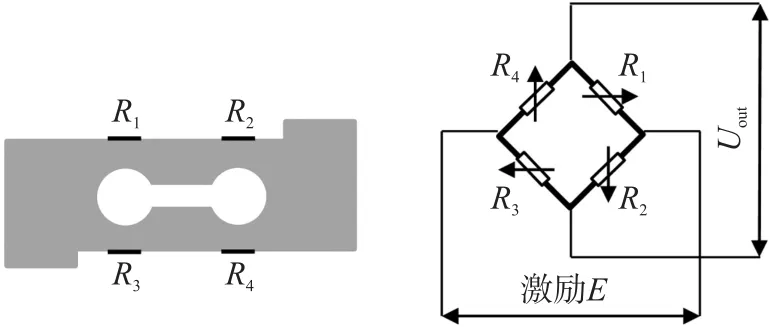
图1 悬臂梁式称重传感器核心部分简图
应变电桥如图1(b)所示,当悬臂梁一端受到压力时,产生形变,贴在其上的应变片的电阻发生改变,这使应变电桥的输出电压与悬臂梁受到的压力呈正相关[9-10]。
应变电桥的输出公式为:
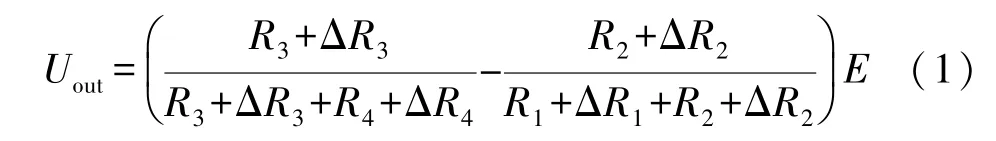
式中:Uout是电桥输出电压值、ΔR为应变片因形变而改变的电阻值、E为激励电压、R1到R4为四个应变片未形变时的电阻值[11]。并且R1=R2=R3=R4=R,ΔR1=ΔR2=ΔR3=ΔR4=ΔR,则:

据式(2)可知由于R、E为常数,所以Uout和ΔR成正比关系,得到应变电桥的输出电压即可计算得到悬臂梁所受压力的大小,从而推出重物的质量。
1.2 姿态传感器
姿态传感器采用维特智能公司的JY系列三轴加速度传感器,内置MPU6050加速度角度传感器,可输出芯片所在平面的X轴和Y轴与水平面之间的夹角φx和φy(正半轴在水平面上方时角度为正,在水平面下方时角度为负)如图2,角度精度为0.05°。
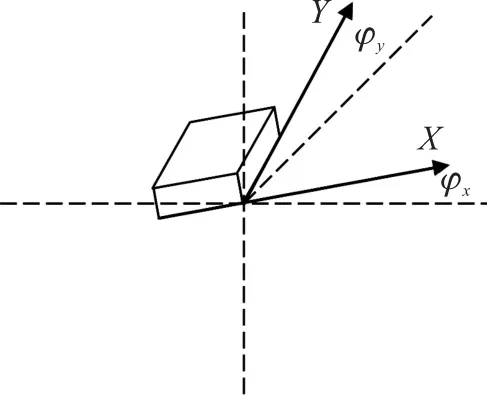
图2 姿态传感器X轴、Y轴与水平面的关系
利用姿态传感器输出的两轴角度,可以通过式(3)计算出姿态传感器所在平面与水平面之间的夹角φ(φ为锐角,在水平面上方为正,在水平面下方为负)。
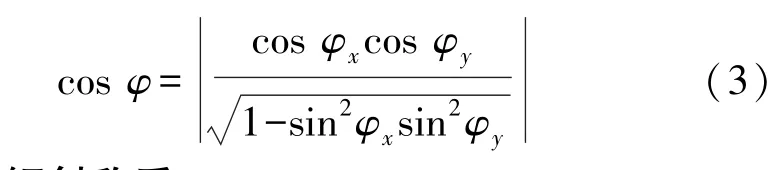
1.3 全周倾斜称重
本文研究以量程为30 000 g、分辨率为5 g的双孔悬臂梁台案秤为例。当倾斜角度超过12°时,秤面上的被称重物会自然下滑,无法称重,所以秤的倾斜角度范围设为φ∈[-12°,12°]。同时姿态传感器安装在秤上,并与其底座处于同一平面内。
1.3.1 悬臂梁式电子秤的全周倾斜
悬臂梁式电子秤的全周倾斜可以分为以下三种:如图3中(a)、(b)、(c)所示,分别为绕着孔轴线倾斜、孔轴线倾斜和前两种倾斜的叠加倾斜。
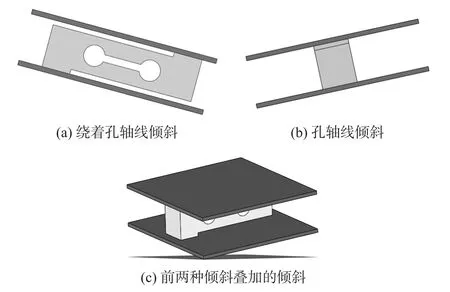
图3 悬臂梁式电子秤的全周倾斜分类
在电子秤的底座平面内建立直角坐标系如图4所示。其中X轴为双孔悬臂梁孔轴线的平行线;图中射线表示秤的倾斜方向,其与X轴的夹角设为θ;并且此直角坐标系与姿态传感器的直角坐标系重合。因为倾斜角度φ有正负,所以倾斜方向θ在第一象限和第三象限的倾斜是相同的,在第二象限和第四象限的倾斜是相同的,这样θ∈[0,180°]即可表示全周倾斜的所有倾斜方向。

图4 倾斜方向示意图
当θ=0时,为电子秤在X轴方向倾斜,如图3中(b)所示,此时设电子秤与水平的夹角为倾斜角度φ=φx,其中φx为X轴与水平面的夹角。
当θ=90°时,为电子秤在Y轴方向倾斜,如图3中(a)所示,此时设倾斜角度为φ=φy,其中φy为Y轴与水平面的夹角。
当θ∈(0,90°)∪(90°,180°)时,为电子秤在前两种倾斜方向叠加倾斜,如图3中(c)所示,此时φx,φy,θ与φ的关系如图5所示。
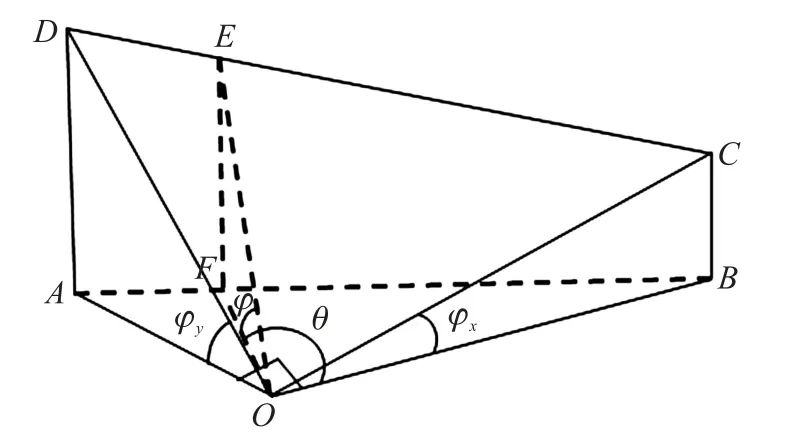
图5 倾斜角度φ与φx,φy和θ的关系
建立空间直角坐标系,并延长AB、DC交于点P,如图6所示。

图6 建立空间直角坐标系后的图
利用解析几何知识通过计算可以得到如下关系:

1.3.2 全周倾斜称重误差
质量为M的重物在倾斜角度为φ的平面上如图7所示。重物对平面的压力为重力沿垂直于平面方向的分力F1的平衡力。

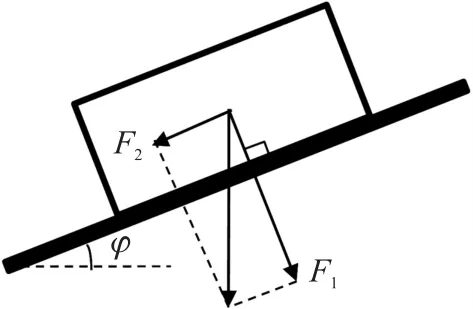
图7 重物在倾斜面平面上的受力分析
由本文1.1可知悬臂梁式称重传感器的输出与其所受到的压力相关。在重物质量M和倾斜方向θ一定的情况下,倾斜角度φ增大时,压力Fn减小,此时悬臂梁式称重传感器输出反映的重量与实际重物的重量存在误差,且φ越大误差越大;而在倾斜方向θ和倾斜角度φ一定时,重物质量越大,误差越大;同时对于悬臂梁式称重传感器,在不同的倾斜方向θ下,相同质量,相同的倾斜φ角度称重所产生的误差是不同的。
2 全周倾斜称重误差补偿算法
因为实际的全周倾斜称重输出数学模型是非常复杂的,直接分析倾斜后悬臂梁的物理特性等,难度过大[12]。所以本文依据台案秤的量程和实际称量精度,在一定的静态工作全周倾斜范围内,对模型进行简化。通过称量标准砝码和可控的倾斜平面进行实验,利用输入与输出的关系构建相对简单而准确的输出误差随全周倾斜的变化模型,以寻求快速可行的全周倾斜称重误差补偿算法。
因为在不同的倾斜方向θ下,悬臂梁式称重传感器对倾斜φ角度后所称重产生误差的灵敏度是不同的。结合本文1.3.2中重物在倾斜平面上的受力分析,设称重时传感器输出电压AD转换值为U,相同重量水平称重时传感器输出电压AD转换值为U0,则设
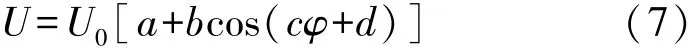
其中设补偿曲线
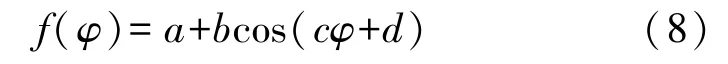
式中:a,b,c,d为待定系数通过实验数据拟合确定出最优估计值。
则有误差
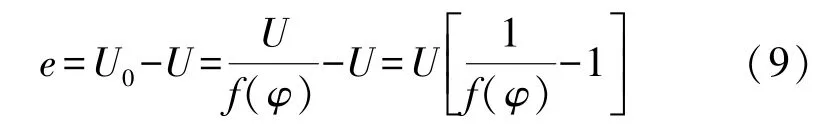
根据式(7)、式(8)和式(9)即可计算出误差的估计值,用以补偿倾斜称重所带来的误差。
在不同的θ下,待定系数a,b,c,d是不一样的,但在同一θ下,待定系数a,b,c是常数。其中由于悬臂梁自身结构的问题,在θ≠0或180°时,随着所称重物质量的增加,悬臂梁会自然向θ=90°的方向倾斜一定角度。
所以需要在θ≠0或180°时,将补偿曲线f(φ)向左平移一段距离d,此距离由重物质量的导致悬臂梁向θ=90°方向自然倾斜的角度所决定。现在分类讨论对应的误差补偿方法如下。
2.1 在X轴方向倾斜,即θ为0时
此时φy=0,φ=φx,倾斜状态如图3(b)所示,随着所称重物质量的增加,此方向上的倾斜角度φ不会增加,所以d也为常数。通过实验记录秤在5 kg、10 kg、15 kg、20 kg和25 kg的砝码下称重时不同倾斜角度φ下传感器输出的电压AD转换值U和水平状态下的U0。
结合式(7)和式(8),利用获得的大量实验数据,拟合出此时的补偿曲线:
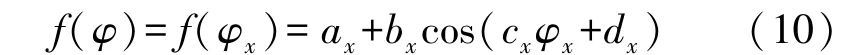
根据图8拟合的曲线可知a,b,c,d的最优估计值为:
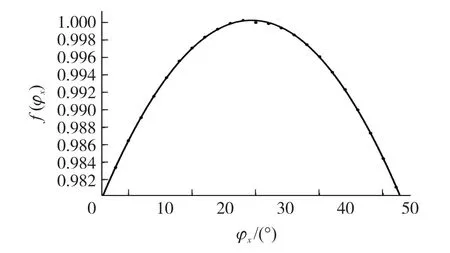
图8 θ=0时拟合的f(φ)的曲线图

把式(11)代入式(10),得到θ=0时的补偿曲线f(φx),再根据式(9),即可计算出该倾斜情况下的误差ex。
2.2 在Y轴方向倾斜,即θ为90°时
此时φx=0,φ=φy,倾斜状态如图3(a)所示,此方向上随着所称重物质量的增加,秤台面的倾斜角度会增加,所以需要找到重物质量M和秤台面的倾斜角度φd之间的关系。因为M和U是正比关系,所以只需找到U和φd之间的数学关系即可。
通过实验记录秤在水平状态下称重时,随着重量的增大,传感器输出电压AD转换值U和秤台面的倾斜角度φd。
根据图9,利用多项式来模拟这种过程,得到φd和U的关系:
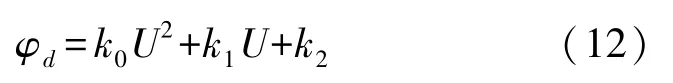
式中:k1,k2,k3通过实验数据和图9的曲线拟合能得到它们的估计值为:
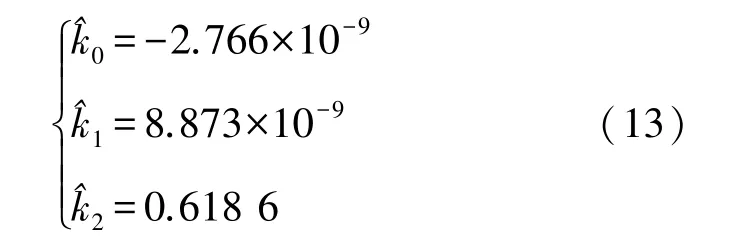

图9 φd关于U的曲线
将式(13)代入式(12),即可得到φd和U的数学关系模型。在此中倾斜情况下φd反映在补偿曲线f(φ)上,得到如下公式:
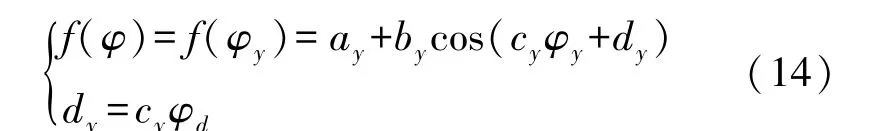
同本文2.1中的过程,通过实验记录秤在5 kg、10 kg、15 kg、20 kg和25 kg的砝码下称重时不同倾斜角度φy下传感器输出电压AD转换值U,后进行实验数据处理拟合出此种倾斜下的补偿曲线。
由式(14)和图10拟合的曲线,可得到此种倾斜下a,b,c,d的估计值:
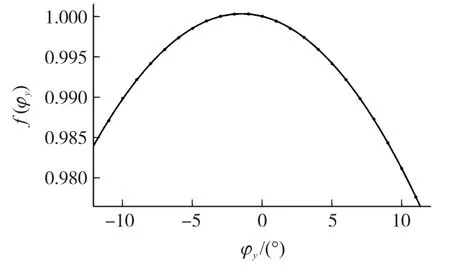
图10 θ=90°时拟合的f(φ)的曲线图
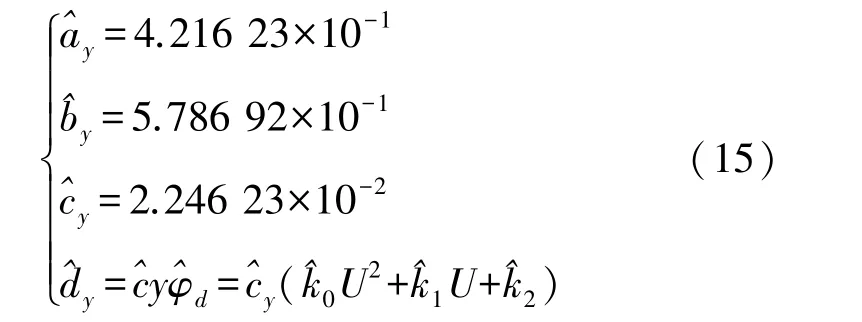
将式(13)、式(15)数据代入式(14)即可得到θ=90°时倾斜的补偿曲线,结合式(9)和U能计算出这种倾斜情况下输出的误差ey用以补偿。
2.3 在其他方向倾斜,即θ∈(0,90°)∪(90°,180°)时
此时φx,φy∈[0,12°],倾斜状态如图3(c)所示,这种倾斜情况可以看作是图3(a)和(b)这两种倾斜方式的叠加。
设此时倾斜称重的误差为exy,由式(9)可知:
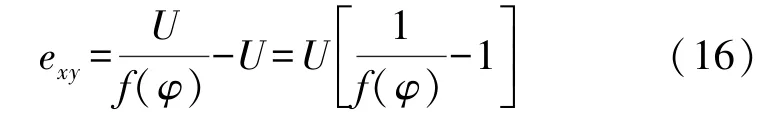
据本文2.1、2.2和式(9)可得:

据式(8)可知补偿曲线的特性由待定系数a,b,c,d决定,a,b决定补偿曲线的幅值;c决定补偿曲线的频率;d决定补偿曲线的相位。
根据本文1.1和1.3.2,在一般理想条件下:
悬臂梁电子秤倾斜称重输出的值只会小于水平称重输出的值,那么补偿曲线的幅值都为1,可将a,b忽略;随着所称重物质量的增加,悬臂梁形状几乎不变,则d=0。悬臂梁在不同倾斜方向上倾斜称重灵敏度不变,c=1,则:

将式(18)代入式(17),得:
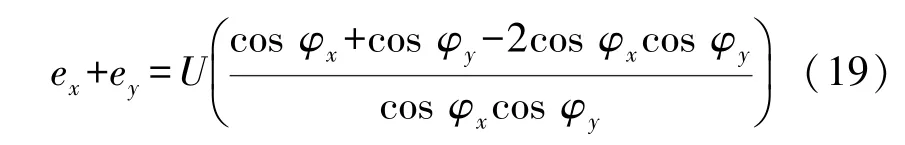
由式(3)和式(5)可知:
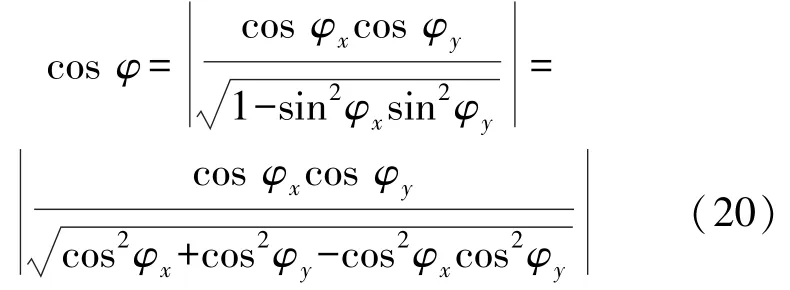
cosφx,cosφy为正,式(20)去掉绝对值并结合式(18)代入式(16)。
所谓的“三分法”是指经济后果观存在零经济后果、正经济后果、和负经济后果。零经济后果实质上就是“信息中立”,其内涵是会计信息与所反映的客观经济事实的价值运动相一致,不带有任何偏见,客观独立公正。正经济后果是指会计信息系统充分考虑利益相关者的信息需求,该信息具备相关性、可靠性,有利于利益相关者的投资及其相关决策,能够帮助他们作出科学合理的决策,维护他们的利益;而负经济后果是指会计信息扭曲了企业的财务状况、经营成果及其现金流量状况,误导利益相关者的投资决策,导致其投资失当,造成资源浪费。
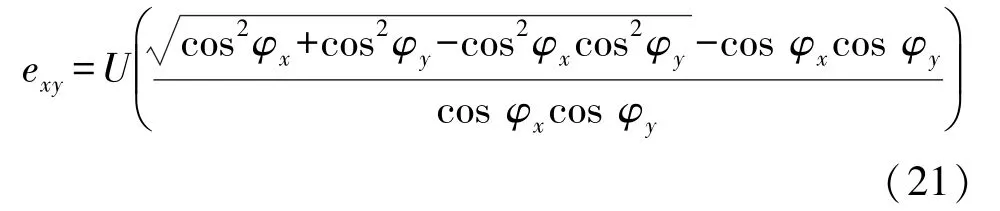
设在一般理想条件下,秤在任意倾斜方向θ上倾斜任意角度φ时,称重误差exy与本文2.1和2.2中算法得出的误差的和(ex+ey)之间的偏差量为p,则:

设n=cosφx,m=cosφy,那么n,m∈[0,1],式(22)为:
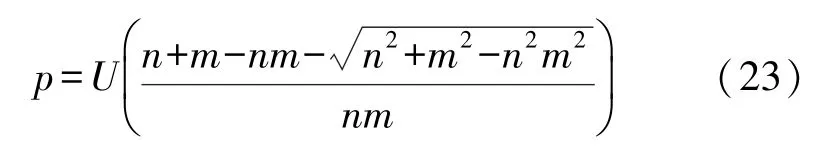
设利用MATLAB分析函数如图11所示,可知当n和m越小,g(n,m)越大,并且当n和m接近0(φx和φy接近90°)时g(n,m)为无穷大;但当n和m变大时(φx和φy变小),g(n,m)的值急剧变小靠近0,n和m越大,g(n,m)越接近0,当n或m=1(φx或φy为0)时,g(n,m)=0。

图11 g(n,m)曲面图
在应用中φx,φy∈[-12°,12°],所以n,m∈[0.9781,1],并且φ∈[-12°,12°],根据式(3)和(5)进一步限定n和m的范围,得到图12所示的g(n,m)曲面图。
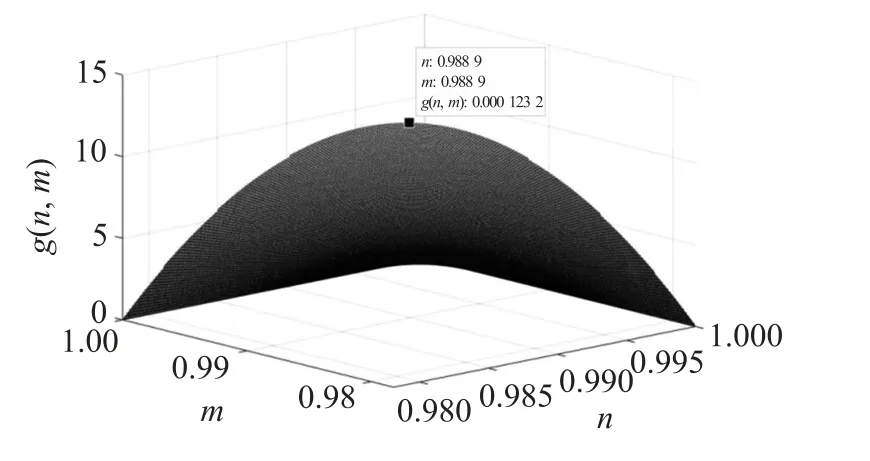
图12 进一步限定n和m的范围的g(n,m)曲面图
可知n=m=0.988 9时,g(n,m)为最大值1.232×10-4,重物质量M和双孔悬臂梁传感器输出的电压AD转换值U是正比关系,式(23)的U可以直接用M替换,此时最大偏差为:

即理论上用ex+ey来代替exy,最大偏差为1.232×10-4倍的量程,对于一般台案秤的精度要求,此偏差可忽略。所以可直接用本文2.1和2.2中的算法来计算其他倾斜方向上倾斜称重时的误差:

在实际生产过程中,因加工工艺的差异性,不同类型的悬臂梁式电子秤的各倾斜称重补偿曲线的系数必然存在差异,但悬臂梁式电子秤的称重原理是一致的,本文所述的补偿算法是从悬臂梁式称重传感器的称重原理上分析提出的,适用于绝大多数市面上已流通广泛的悬臂梁式电子秤类型。所以只需对已有类型的悬臂梁式电子秤增添姿态传感器模块,并在所要生产的悬臂梁式电子秤出厂前,对各款悬臂梁式电子秤进行上述全周倾斜称重误差补偿过程,将获取的相关参数如式(11)、式(13)、式(15)存入各自MCU的Flash中。在MUC循环运行的主程序中写入补偿算法程序,秤称量时MCU会自动根据姿态传感器采集到的倾斜角度和悬臂梁传感器输出的电压值,调用参数并代入补偿算法式(25)得到称重值,从而在显示器上显示准确的称量结果。而使用者只需给电子秤通电即可进行全周倾斜称重。
3 实验验证

图13 全周倾斜称重检验现场
台案秤分别为从0到165°每隔15°的倾斜方向上,倾斜角度从-12°到12°每隔1°加载30 kg砝码,记录加载前后的空载和满载示值,全周倾斜称重误差补偿前后的部分结果如表1和表2所示。

表1 全周倾斜称重误差补偿前的各倾斜情况下示值

表2 全周倾斜称重误差补偿后的各倾斜情况下示值
由表1和2可见,在全周倾斜称重误差补偿前空载的最大示值绝对误差达50 g,满载的最大示值绝对误差达650 g,远远不能满足称量精度要求。采用本文算法补偿后,空载的示值绝对误差为0,满载示值绝对误差≤5 g,符合国家标准《GBT7722-2005电子台案秤》规定的台案秤受倾斜引起的变化量的指标。
4 结论
本文针对现阶段悬臂梁式电子秤的倾斜称重方面的研究内容少、研究不充分(只考虑单一倾斜方向)、实际应用价值低的情况,提出了一种全周倾斜(包含三种倾斜类型)的称重误差补偿算法。经实验验证结果表明,该种算法可以有效地补偿秤全周倾斜称重带来的误差,满足国家标准的指标,并且得到的补偿算法计算简便、容易实现。
