星箭界面环形分布随机动载荷频域识别

吴邵庆 何子豪 尹 健 陈树海

(1东南大学土木工程学院， 南京211189)(2东南大学江苏省工程力学分析重点实验室， 南京211189)(3东南大学江苏省空天机械装备工程研究中心， 南京211189)(4上海卫星工程研究所， 上海201109)

航天器与运载火箭界面的载荷特征是航天器结构设计和试验考核的重要依据[1].安装力传感器直接测量界面载荷会干扰整体结构的动力学特性，增加系统负重并降低结构设计的可靠性.发展适用于星箭连接界面呈环形非均匀分布特征的随机动载荷识别方法具有重要意义.

在星箭连接界面处的动载荷识别方法主要包括2类：① 基于星箭连接环的理论模型和星箭连接环处应变响应反演星箭界面载荷[2]；② 利用星箭结构有限元模型以及结构动响应来反演界面载荷[3-4].在这些界面力识别研究中，星箭界面载荷采用集中力或均匀分布力来描述.为了识别沿连接环非均匀分布的界面动载荷，尹健等[5]利用B样条函数拟合非均匀分布力的分布函数，在时域内实现了星箭连接界面处非均匀分布动载荷的时间历程识别.

航天器发射过程中处于随机振动环境[6]，针对星箭连接界面处的随机载荷，识别其统计特征比识别其时间历程更有意义.随机动载荷识别方法主要分为适用于平稳随机载荷的频域识别方法[7]和可以更方便考虑时变的载荷统计特征的时域识别方法[8]两类.针对识别过程中的矩阵病态问题，Jia等[9]提出了一种频域随机动载荷识别方法，同时考虑测量噪声和系统频响函数误差.He等[10]考虑结构参数区间不确定性，提出了多点随机动载荷的频域识别方法.Wu等[11-12]基于结构随机有限元模型，提出了随机动力学系统上的随机动载荷识别方法，并将其应用于含不确定性参数卫星结构的随机基础激励识别中[13]；然而，该研究中基础激励假设为沿环形均匀分布的随机动载荷，忽略了其空间分布非均匀的特征.

为了识别星箭连接处沿环形非均匀分布的随机动载荷，本文引入B样条函数拟合环形分布随机动载荷的空间分布，分别结合直接求逆法和逆虚拟激励法，提出了环形分布随机动载荷识别新方法.利用数值仿真算例，验证该方法的有效性，并进一步讨论了各种影响载荷识别结果精度的因素，为星箭界面随机动载荷识别提供技术支持.

1 环形分布随机动载荷识别原理

1.1 多点随机动载荷频域识别

对于一个多自由度动力学系统，多点随机激励与随机响应间的关系式为

Syy(ω)=H*(ω)Sxx(ω)HT(ω)

(1)

式中，ω为圆频率；Syy(ω)为系统响应的功率谱密度矩阵；Sxx(ω)为系统激励的功率谱密度矩阵；H(ω)为系统的频率响应函数矩阵.

将式(1)求逆，便可由系统响应的功率谱密度识别多点随机动载荷，这种随机载荷识别方法被称为直接求逆法.计算公式为

Sxx(ω)=H*+(ω)Syy(ω)HT+(ω)

(2)

式中，上标+表示矩阵广义逆.

为了减少载荷识别中的矩阵求逆次数，提高识别效率，Lin等[14]提出了逆虚拟激励法.由于响应的功率谱密度矩阵Syy(ω)为Hermite矩阵(简记为Syy)，可对其进行如下的特征值分解：

(3)

式中，λl和φl分别为响应功率谱密度矩阵的第l个特征值与特征向量；m为矩阵Syy的秩.

动力学系统响应的功率谱密度矩阵为非负定，其所有特征值非负，即有λl>0(l=1,2,…,m).令

(4)

则响应的功率谱密度矩阵Syy可重新表示为

(5)

(6)

式中，t为时间.

(7)

由此，待识别的随机激励功率谱密度矩阵Sxx为

(8)

1.2 基于B样条函数的分布随机动载荷模型

环形连续分布动载荷相当于无数个集中动载荷的环形集合.为了识别分布动载荷，必须对载荷识别问题进行降维处理，常用方法是利用基函数拟合分布动载荷的空间分布函数，如模态振型函数、正交多项式、B样条函数等.B样条函数具有分段、高阶导数连续、首尾闭合等特性，适合用于拟合呈环形分布动载荷的空间分布函数.在区间[x0,xN)上，P次B样条基函数的Cox-de Boor递推表达式定义如下：

(9)

(10)

式中，Ni,p(x)为第i(i=0,1,…,n-1)个p(p=1,2,…,P)次B样条基函数；xi为B样条基函数的节点.

假定环形分布随机动载荷q(x,ω)在各个位置具有相同的功率谱密度函数S(ω)，且空间分布函数B(x)与功率谱密度特征不相关，其功率谱密度Sqq(x,ω)可以表示为

Sqq(x,ω)=[B(x)]2S(ω)

(11)

选取三次B样条基函数Ni,3(x)，具有二阶导数连续的特性.在环形对接面处，将环形分布随机动载荷沿环向分为N段，每段的端点定义为控制点，则总共有N个控制点.利用周期性边界条件，将随机动载荷的空间分布函数B(x)采用B样条基函数拟合，即

(12)

式中，Bi为第i个B样条基函数所对应的系数.B样条基函数对应系数的个数等于控制点个数，也等于沿环向的分段数N.将式(12)代入式(11)可得

(13)

1.3 基于直接求逆法的环形分布随机动载荷识别

(14)

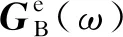
HB(ω)=H(ω)GB(ω)

(15)

式中，HB(ω)为频域动载荷B(x)I(ω)对应的频率响应函数向量.同理，将以B样条基函数Ni,3(x)为分布函数的频域动载荷Ni,3(x)I(ω)对应的频率响应函数向量记为HN(ω).

令SYY(ω)表示环形分布随机动载荷q(x,ω)作用下结构响应的功率谱密度矩阵，则

(16)

引入基于B样条函数拟合的分布动载荷模型，式(16)可以表示为

(17)

式中，A(ω)中第i行第j列元素Aij=BiBjS(ω).

根据式(17)，可由直接求逆法识别矩阵A(ω)，即

(18)

利用矩阵A(ω)中的元素和B样条基函数Ni,3(x)，根据式(11)便可重构环形分布随机动载荷的功率谱密度Sqq(x,ω).

1.4 基于逆虚拟激励法的环形分布随机动载荷识别

由式(11)中的环形分布随机动载荷功率谱密度Sqq(x,ω)构造如下的虚拟激励：

(19)

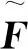
(20)

将式(12)和(19)代入式(20)，交换积分与求和次序可得

(21)

(22)

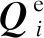
令分布载荷作用宽度内所覆盖的有限单元个数为n，式(22)可改写为如下矩阵形式：

(23)

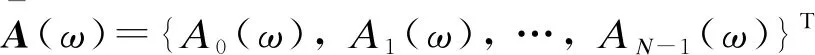
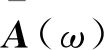
(24)

HN(ω)=H(ω)Q

在载荷识别过程中，已知各测点随机动响应的功率谱密度矩阵SYY(ω)，由式(5)可得

(25)

式中，Yl(ω)为SYY(ω)矩阵的第l个特征值开方与特征向量的乘积.

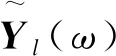
(26)

求解式(26)时要求测点数不小于控制点个数，即测点数不小于待识别的B样条基函数系数个数N.由于矩阵往往存在病态的现象，在系数向量Al(ω)的求解过程中，可以利用正则化方法提高矩阵HN(ω)的广义逆运算的求解精度.本文采用基于截断奇异值分解(TSVD)的正则化方法，设置一个阈值σλ，将矩阵HN(ω)中小于σλ的奇异值全部置零，以消除小奇异值对识别结果误差的影响.

根据Al(ω)可求得系数矩阵A(ω)为

(27)

将系数矩阵A(ω)中的元素Aij=BiBjS(ω)代入式(13)，即可重构出待识别环形分布随机动载荷的功率谱密度Sqq(x,ω).

相比直接求逆法需要在每个频率点对矩阵HN(ω)进行2次求逆操作，逆虚拟激励法仅需要求1次矩阵HN(ω)的逆，计算量大幅减少.尤其是在矩阵HN(ω)维度较大时，识别效率显著提高.

2 仿真算例

2.1 卫星结构模型与分布随机基础激励

以某卫星结构模型为研究对象，验证所提出的载荷识别方法，并讨论不同影响因素对识别结果精度的影响.根据表1中的卫星结构模型尺寸参数，建立如图1所示的卫星结构有限元模型.在底部施加约束，仅释放Z方向的平动自由度.图2给出了底座的有限元网格节点以及控制点编号.由图可知，在卫星结构有限元模型中，底座星箭连接界面处沿环向划分为24个单元，按逆时针方向设置有限单元节点编号1～24.将载荷作用环形区域分段，每段端点定义为控制点，控制点沿顺时针编号C1～C4.图中还给出了沿环形分4段时所选取的控制点方案，其他分段方式也可类似地等距选取控制点.

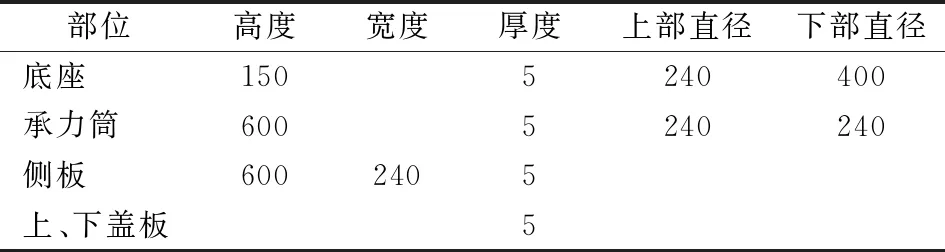
表1 卫星模型尺寸和材料参数 mm

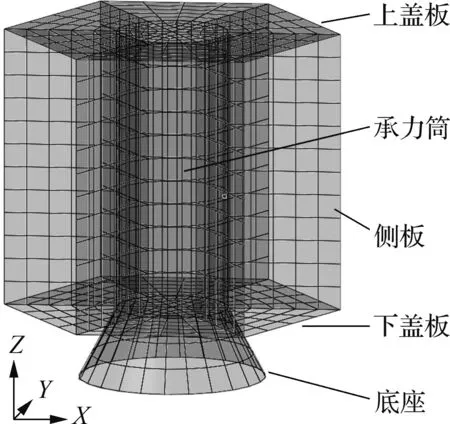
图1 卫星有限元模型

图2 星箭界面连接处有限单元节点编号与4个控制点时控制点编号

用于载荷反演的结构加速度响应测点设置在结构的主要传力路径(即承力筒)上，以保证结构响应对星箭界面动载荷具有较高的灵敏度.测点分布及编号S1～S8见图3.

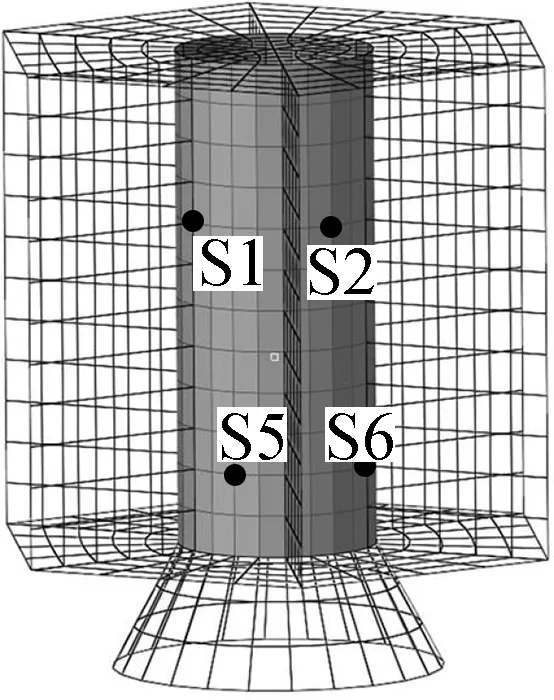
图3 测点分布图

由于火箭和卫星由星箭连接环连接，火箭在发射和飞行过程中的振动主要由纵向模态和弯曲模态控制，分别对应星箭连接环处的线振动和角振动.线振动和角振动的叠加会使界面动载荷沿连接环呈现非均匀分布.载荷分布特征主要受角振动影响，一般认为其随火箭弯曲振动沿环向呈现反对称分布.因此，假设载荷分布函数B(x)为

(28)

用B(x)表征沿环形对接面分布的载荷分布函数时，自变量x代表从图2中节点1为起始点，沿周长顺时针方向的弧坐标.函数中常数部分由纵向振动引起，三角函数部分沿环向呈现反对称分布.

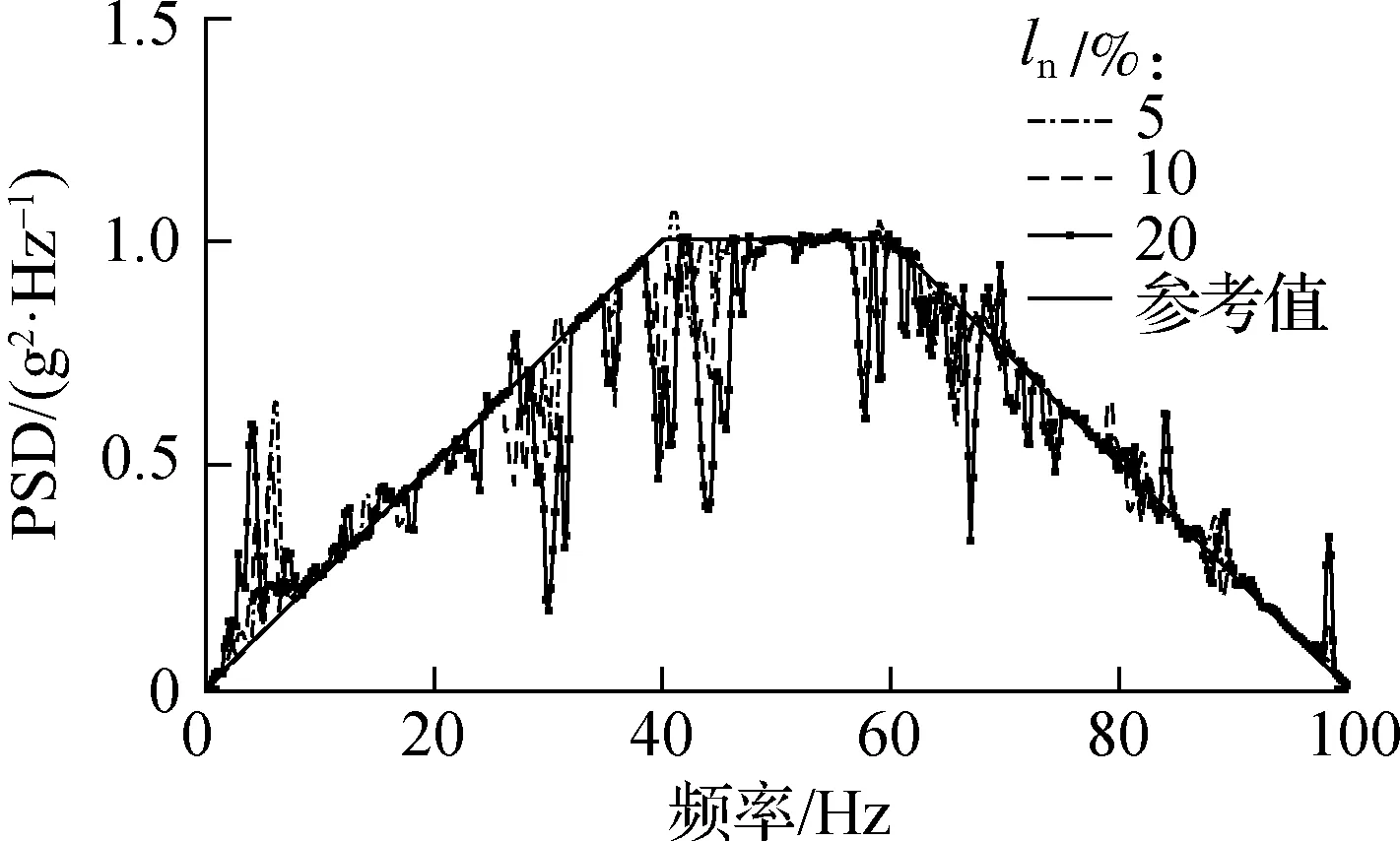
激励的功率谱密度函数S(ω)独立于其空间分布函数，根据发射主动段卫星底板处加速度响应测量数据[15]，采用图4中的1～100 Hz内简化的梯形谱作为卫星底部随机加速度激励的自功率PSD谱.

图4 随机基础加速度激励的自功率谱

本文中所用卫星结构模型的第1阶整体蒙皮呼吸、第1阶整体扭转和第1阶整体弯曲模态的频率分别为4.14、4.37、5.57 Hz.模型由于壁板较薄，存在诸多壁板局部呼吸模态.随机激励频段为1～100 Hz.因此，在仿真分析中，考虑了100 Hz以内的所有结构模态，共316阶，各阶模态的阻尼比设定为0.002.

为了量化识别激励精度的空间分布误差，利用下式表征识别值向量Rid与参考值向量Rref间的相对误差Re：

(29)

2.2 识别方法验证

将2.1节中定义的环形分布随机基础激励作为参考载荷沿Z方向施加于卫星结构模型底部，开展随机振动分析，获得测点处仿真加速度响应的功率谱密度.将仿真响应作为载荷识别过程中的输入，利用本文方法识别环形对接面上的分布随机基础激励载荷，并与参考载荷对比，验证识别方法的有效性.

为了方便对比，将识别所得各点功率谱密度Sqq(xi,ω)取平均值，作为Sqq(ω)的识别值，计算各节点处Sqq(xi,ω)的均方根(RMS)误差与Sqq(ω) 的RMS误差的比值，得到整体空间分布B(x).在实际识别过程中，数值精度、矩阵病态等可能导致所识别的功率谱密度在部分固有频率点处出现异常跳动，故舍弃这些个别的异常跳动值，利用附近识别值的插值代替.结合本文算例情况，舍弃功率谱密度识别值中大于2 g2/Hz或小于0的值.

将载荷分布函数沿对接环分为4段，则存在4个控制点，即N=4.选取三次B样条基函数，通过在结构上顺时针定义编号为C1～C4的4个控制点，根据选取测点处的加速度响应信息，分别使用直接求逆法(DI)、逆虚拟激励法(IPE)和带正则化方法的逆虚拟激励法(IPER)，反演得到卫星底座所受的随机基础加速度激励载荷的功率谱密度和空间分布.图5(a)给出了基础加速度激励功率谱密度识别值Sqq(ω)与参考值的对比.结果显示，基于3种方法的随机动载荷功率谱密度识别值在总体趋势上与参考值都吻合良好，但不同方法的识别结果在个别频率点附近存在差异.无噪声情况下，采用DI方法、IPE方法、IPER方法识别得到各节点处随机激励功率谱密度Sqq(ω)的相对误差分别为0.00%、0.00%和1.37%，最大相对误差分别为0.17%、0.17%和1.67%，最大相对误差分别出现在节点19、节点19和节点5.计算各节点处功率谱密度识别结果的RMS值，按Sqq(ω) 的RMS值归一化，可得到随机基础加速度激励的空间分布函数识别值.随机基础激励空间分布函数B(x)的识别值与参考值对比见图5(b).由图可知，基于3种方法的随机动载荷空间分布识别值同样都吻合良好.根据式(29)，DI方法、IPE方法、IPER方法的相对误差最大值分别为0.09%、0.09%和0.22%.

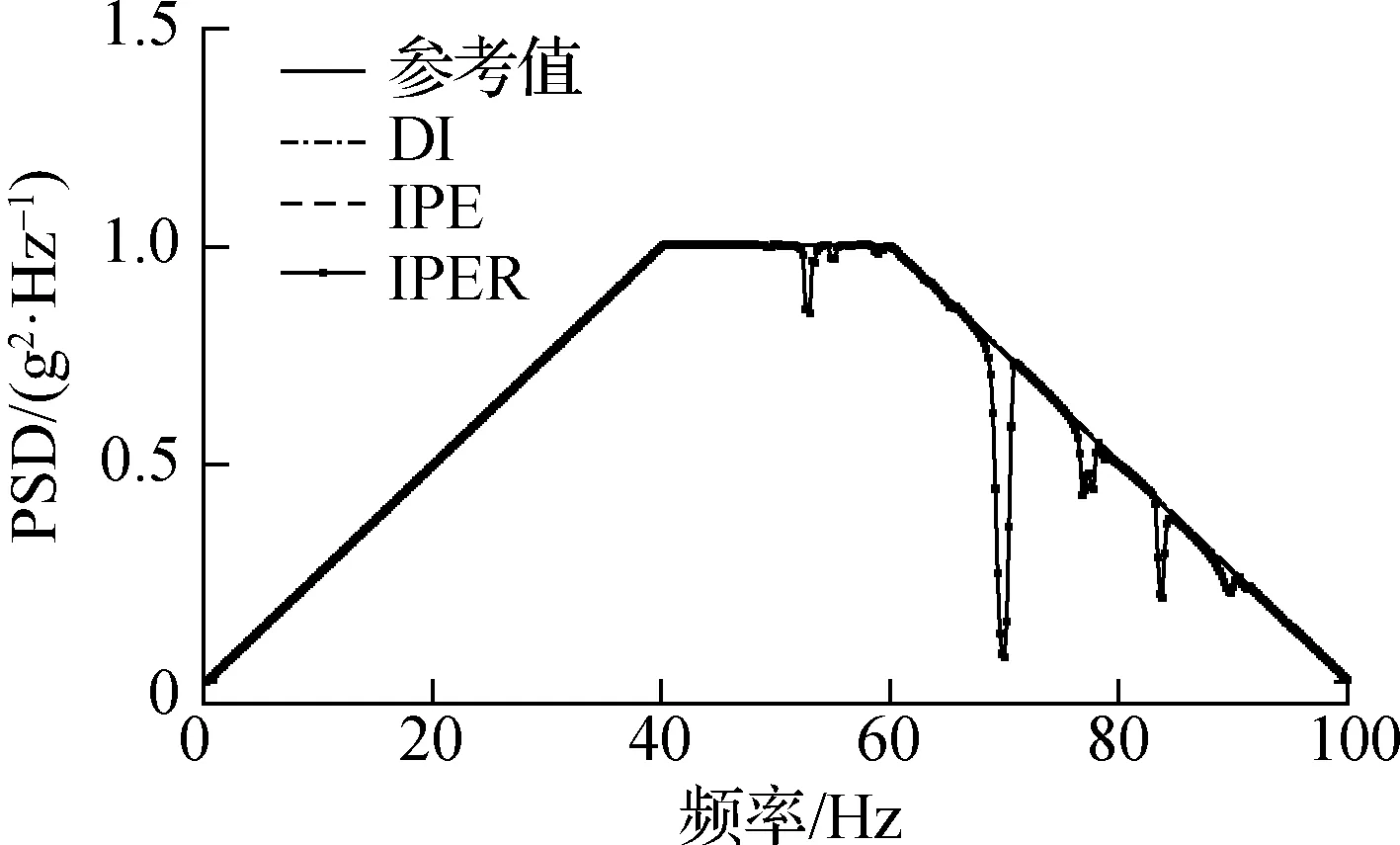
(a) 功率谱密度

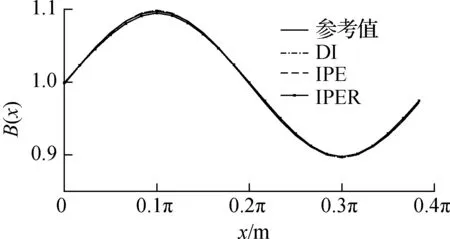
(b) 空间分布函数

由此可见，本文方法能够基于卫星结构少量测点处的随机响应功率谱密度，识别卫星底部非均匀分布的随机基础加速度激励.在无噪声工况下，3种方法均能较好地识别随机激励功率谱密度和空间分布，其中DI方法效果最佳.究其原因在于，对于DI方法，其识别公式(18)是对响应计算公式(17)直接求逆，在无噪声情况下精度较高；对于IPE方法，尽管需要分解矩阵SYY并舍弃数值误差引起的特征值为负值的特征对，可能会对识别结果造成偏差，但在无噪声工况下影响较小；而IPER方法则需要在此基础上进一步分解矩阵G并舍弃部分奇异值以进行正则化处理，从而导致个别固有频率点附近载荷功率谱密度识别出现偏差.观察各节点功率谱密度识别值的相对误差可知，最大相对误差都位于控制点处，且该控制点处于载荷区域内载荷最大值或最小值位置.这是因为在控制点对应的节点处，受本控制点的影响最大.相比控制点处节点，其他节点处的识别结果受到误差较小控制点的影响，识别精度更高.

2.3 测量噪声对识别精度的影响

实际工程中，测点处采集的加速度响应信号会受到噪声污染，需讨论测量噪声水平对各识别方法识别精度的影响.利用下式在卫星结构加速度响应功率谱密度中添加噪声：

Yn=Yc+lnstd{Yc}rand(-1,1)

(30)

式中，Yc和Yn分别为未添加和已添加噪声的各测点加速度响应功率谱密度矩阵；std()为标准差；ln为噪声水平；rand(-1,1)表示在区间[-1,1]上的随机数.

当噪声水平ln分别取5%、10%、20%时，基础加速度激励均方根RMS识别误差见表2.由表可知，识别误差总体随着噪声水平的增大而增大，但各工况下均能得到较准确的识别结果.DI方法和IPE方法在低噪声水平时具有较好的识别效果，但识别的RMS值和空间分布误差随着噪声水平增大而明显增大.IPER方法则由于引入了正则化方法，较好地抑制了测量噪声对识别结果的影响，在3种方法中对测量噪声的鲁棒性最好.因此，在后续讨论中，仅针对含测量噪声工况下表现最好的IPER方法开展讨论.

IPER方法识别所得的功率谱密度见图6(a).由图可知，除了少数几处存在较大偏差外，其余各频率段都具有较好的识别效果.图6(b)为不同噪声水平下采用IPER方法所识别的载荷空间分布函数B(x)与参考值对比.由图可知，噪声水平的增加仅使B(x)的识别误差略微增加，说明IPER方法对噪声具有较好的鲁棒性.

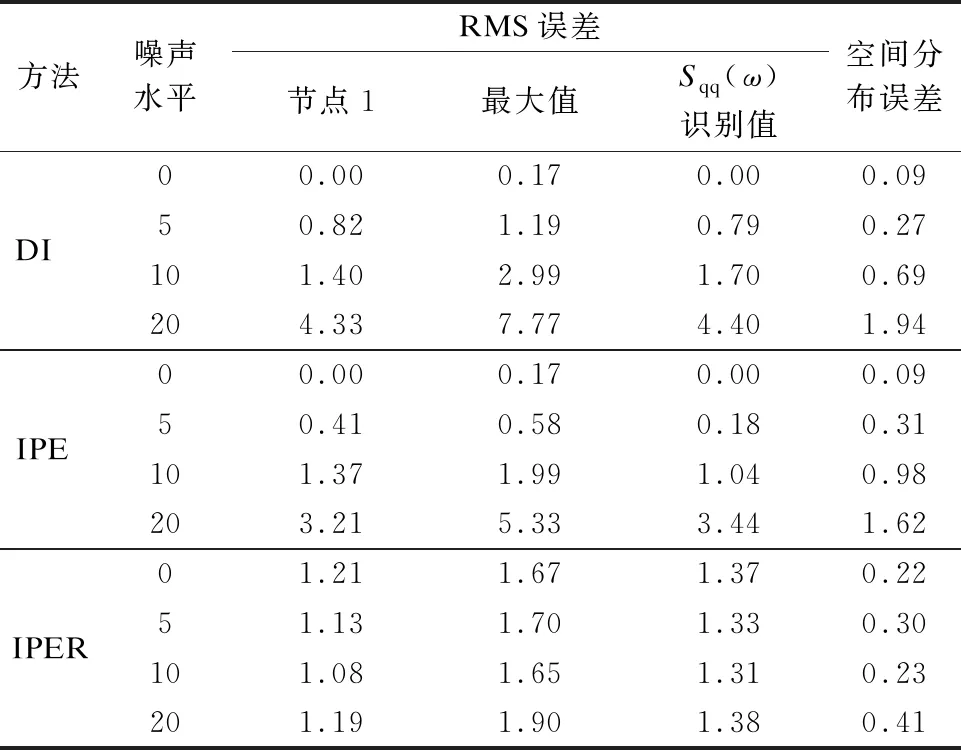
表2 不同噪声水平下基础加速度激励识别误差 %

(a) 功率谱密度

(b) 空间分布函数

2.4 测点数量对识别精度的影响

基于2.2节中的仿真算例，在控制点数为4、噪声水平为5%的情况下，选取不同测点数量(4、8、12)开展基础加速度激励反演，讨论测点数量对激励功率谱密度和载荷空间分布识别结果的影响.测点选择方案见表3.

表3 三种工况下的测点选择方案

表4给出了不同测点数量工况下基础加速度激励功率谱密度RMS识别误差以及载荷空间分布的误差.由表可知，在控制点数量不变的情况下，满足测点个数大于或等于待识别B样条基函数系数个数的条件时，3种工况下动载荷功率谱密度识别的RMS误差均小于2%，动载荷空间分布识别的误差小于2%，均能较为准确地重构出环形分布动载荷的功率谱密度与空间分布.随着测点数量的增加，IPER方法的动载荷功率谱密度识别精度小幅提升，但空间分布误差却有可能增大.这是因为随着测点数量的增加，动载荷功率谱密度的识别结果中较大偏差的值减少，如70 Hz处的异常识别值在测点数量增加后得到了良好抑制，但各节点处可能出现更多小偏差，影响RMS值的分布，进而影响空间分布的识别结果.

表4 不同工况下激励识别误差 %

此外，随着测点数量的增加，用于识别的矩阵HN(ω)维度增大.由于不同测点的频响函数曲线具有相似特征，矩阵HN(ω)的行(列)向量相关性将随着矩阵维度的增加而增加，从而增大矩阵的条件数，导致求解过程中的误差增大.DI方法和IPE方法的识别精度低于IPER方法，测点数量为4、8、12时，DI方法的功率谱密度Sqq(ω)识别值的相对误差分别为0.79%、5.29%、3.99%，IPE方法的相对误差分别为0.18%、6.21%、2.39%.这表明在分布随机基础激励特征较为简单的工况下，使用少量测点即可保证动载荷识别的精度，增加测点数量反而可能会引起识别效果下降.因此，在后续的控制点数目讨论中，令测点数量等于控制点数量.同样，在3种方法中，IPER方法具有最好的识别精度.

2.5 控制点数量对识别精度的影响

基于2.2节中的仿真算例，噪声水平为5%的情况下，选取不同控制点数量开展基础加速度激励反演，讨论控制点数量对激励功率谱密度和空间分布识别误差的影响规律.由式(13)可知，控制点数量与环形分布载荷模型中待识别的B样条基函数系数个数相等.当控制点数量增加时，令测点数量对应增加且等于控制点数量，以满足测点数量不小于待识别B样条基函数系数个数的要求.

表5给出了不同控制点数量下基础加速度激励功率谱密度和载荷空间分布的识别误差.由表可知，增加控制点数量会降低载荷的识别精度.文献[9]指出，增加控制点数量能够提高对载荷分布函数的拟合精度和识别精度.相较于载荷功率谱识别结果，载荷空间分布识别结果对控制点数量更为敏感，其误差在此工况下反而随着控制点数量的增加而增大.这是因为本文假设的激励分布函数形式简单，设置4个控制点已满足识别精度的要求，能够较好地拟合载荷的空间分布，使空间分布的识别误差较小.增加控制点数量将导致待识别的系数个数增加，影响识别过程中求逆矩阵的性态，导致识别误差增大.

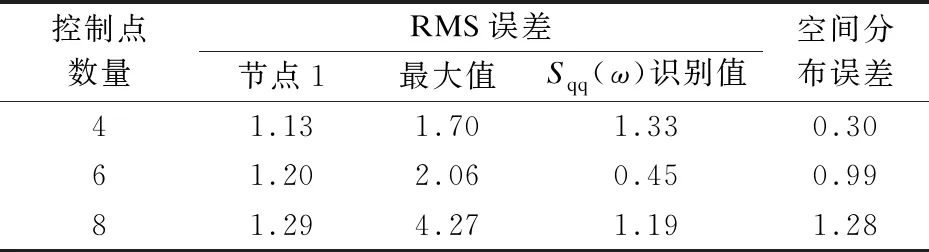
表5 不同控制点数量下基础加速度激励识别误差 %

进一步研究空间分布函数更复杂工况下的载荷识别.假设采用相同的功率谱密度函数，载荷空间分布函数为

(31)

该工况下，基于不同控制点数量的空间识别误差见表6.由表可知，空间分布较复杂时，适当增加控制点能够减小载荷空间分布的识别误差.

表6 基于不同控制点数量的空间识别误差 %

3 结论

1) 本文基于B样条函数对载荷空间分布的拟合，结合直接求逆法和逆虚拟激励法，提出了环形分布随机动载荷识别方法，并将其应用于星箭连接环处的分布随机动载荷识别.通过仿真算例研究，证明所提方法能够基于少量结构加速度响应数据识别星箭连接界面处的环形分布随机动载荷，保证了识别载荷的空间分布连续性，且相比传统方法考虑了载荷沿环形的非均匀分布.

2) 在响应数据受噪声干扰时，对比3种识别算法可知，DI算法对仿真加速度响应中噪声的敏感程度最高，较高噪声水平下误差较大；IPE算法通过对矩阵的分解改善了求解效率，且对噪声的敏感程度有所下降；IPER算法在IPE算法的基础上引入了正则化方法，具有更好的噪声鲁棒性.

3) IPER算法利用少量测点和控制点，获得了较高的激励功率谱密度和空间分布识别结果.在不同噪声、测点数量、控制点数工况下，激励的功率谱密度和空间识别误差均小于2%.控制点数量的增加理论上能提升B样条函数拟合载荷模型表征更复杂的载荷分布特征的能力，但是也会增加待识别参数个数，可能增大识别结果误差.因此，应谨慎增加控制点数量，仅在空间分布较复杂时适当增加控制点数量即可.