一般垄断下厂商最优和社会最优的动态优化比较

宋建朋 钟根元 陈志洪

(上海交通大学 安泰经济与管理学院，上海 200030)

0 引言

随着社会生产力的发展和人民生活水平的提高，消费者对商品的购买力也在不断提高。这为制造业厂商带来了更大的市场，同时也对商品质量和性价比提出了更高的要求。厂商如何进行生产决策，来获得更高的收益、耗费更小的成本是一个值得研究的问题。一方面，一种商品的竞争力越来越多地依赖消费者对其质量、功能、商誉、售后服务等诸多因素的评价，而这些因素的提高，需要企业持续进行技术创新投入；另一方面，通过改进生产技术、科学地进行生产管理，即过程创新，企业可以显著降低商品的生产成本。这两种方式都可以增加企业的生产者剩余，是市场经济中提高企业利润的重要手段。每个创新型企业都会兼顾这两方面的投资，而协调这两方面的投入，使得企业利润或社会福利达到最大化，本质上是一个动态优化的问题。

由于研究方法和模型的差异，长时间以来，研究人员对于两种创新方式的关系有比较大的争论。早期，Utterback和Abernathy(1975)研究了一个企业在特定生产过程的发展状态和其选择的竞争模式下产品创新和过程创新之间的关系。Martinez(1999)、Mantovani(2006)等人的研究表明产品创新和过程创新之间存在互补的关系。但并不是所有的研究都支持这一观点，Lanbertini和Orsini(2015)认为企业是独立进行产品创新和过程创新投入决策的。Rosenkranz(2003)的研究表明，在竞争强度较低时，企业只会采取产品创新，而Weiss(2003)却提出了相反的看法，他认为在竞争强度较高时，企业会有逃离竞争的激励，去投入产品创新。Adner和Levinthal(2001)指出企业会根据市场特征决定如何投入产品创新和过程创新。

随着动态模型研究的不断深入，越来越多的决策因素和市场模型正在被广泛研究。Becker和Egger(2013)研究了技术创新和过程创新对企业出口倾向的影响；Lanbertini和Mantovani(2009)研究了多产品垄断厂商的产品、过程创新的互补关系；Hasnas、Lambertini和Palestini(2014)研究了开放式创新环境中寡头企业的决策；Zhong和Zhang(2017)研究了企业对产品创新、过程创新投入与知识积累和折旧的关系。

虽然目前研究人员关于产品创新和过程创新已经有了很多的发现，但是很少有文章会涉及企业最优决策的定量研究，而最优决策的定量研究无疑可以给合理决策提供很有说服力的参考。所以，本文在保留传统研究内容的基础上，希望通过求解最优决策表达式，给决策方提供更加精确的参考和帮助，并且结合决策路径的表达式，直观地分析一些因素对于决策的影响。总结来说，本文的主要贡献在于：(1)求解出一般垄断市场下企业最优和社会最优时的厂商决策最优路径；(2)证明了一般垄断市场在动态条件下和静态条件下具有相同的结论，更接近一般实际；(3)考察了利率、企业初始值等因素对企业决策的影响。

本文的第一部分，对厂商最优的生产决策进行了求解，并考察了利率、厂商初始值等一些外生变量对结果的影响；第二部分求解了社会最优时的生产决策，并对两者进行了对比，得到了与静态模型相同的结论，证明了动态过程是静态模型更接近实际的推广；第三部分讨论了利率和变量的初始值对企业决策的影响。

1 一般垄断厂商最优决策

根据Pan和li(2016)关于商品需求的理论，商品的销量随着质量的提高而增加。商品的质量越高，消费者对它的评价就越高，需求就会越高。据此可以假设反需求函数具有如下形式：

p=a1+a2q-a3x

(1)

在这里，本文只引入了一个质量变量来影响价格，而在实际市场中，可能存在很多影响价格的因素，如商誉或是售后服务等。零售商可以通过广告等营销手段提高它的商誉，或是通过具有吸引力的售后服务来吸引消费者。这些措施都可以提高产品的市场需求，并且它们之间可能存在互补或是替代关系。但这些策略的研究方法和结论是类似的，为了简化模型，本文只引入一个质量变量，并且设它和需求的关系为线性。

根据Lanbertini和Orsini(2015)的理论，对于企业来说，可以通过投入产品创新，以提高产品的科技含量、功能或是感官体验来提高消费者对产品的评价。但随着时间的推移，新技术的产生使得这些因素变得不那么流行，类似于一种质量“折旧”。所以，企业的产品创新变化由下式决定：

q=k1-δq

(2)

其中，k1是厂商的产品创新投入。另一方面，企业通过过程创新来降低平均成本，带来更多的生产者剩余。但企业的生产成本也会随着设备的老化等问题随时间逐渐上升，所以生产成本的变化函数为：

c=-k2-ηc

(3)

式中，k2是厂商的过程创新投入。企业投入技术创新和过程创新所带来的成本是：

(4)

成本正比于技术投入水平的二次方，是因为这两项投入带来的边际收益是递减的。对于一个特定的厂商，给定决策变量产品创新投入k1、过程创新投入k2、状态变量质量q、生产成本c的初始值k10、k20、q0和c0，模型的最决策优路径就固定下来。接下来对变量的路径进行求解。

企业每个时期的利润为销售额减去生产成本和创新的投入成本：

(5)

设利率为r(t),为了简化模型，可以假设利率在较长时间内保持稳定，即r(t)=r,由Chenavaz(2012)关于企业利润流最大化要求的研究可知：

(6)

所以，当期汉密尔顿函数为：

(7)

根据最优化的一阶条件，以及乘子方程可以列出：

(8)

联立此微分方程组和式(2)、(3)，得到一个七元的一阶线性非齐次微分方程组。其中，未知数为控制变量k1、k2、x，状态变量q、c和共态变量m1、m2。而a1、a2、a3、α、β、δ、η是常数，其数值可以根据行业的统计信息求得。

利用常数变异法进行推导，可以得到控制变量和状态变量的最终解为

其中，k10、k20、q0、c0是对应变量的初始值，λ、f、g分别由式(10)～(13)决定：

μ1λ4+μ2λ3+μ3λ2+μ4λ+μ5=0

(9)

参数部分的含义如下：

(10)

(11)

(12)

将q和x代入式(1)得到价格的表达式为：

(13)

为了简化过于复杂的表达式及结果，可以将解析式里的常数取一些典型的数值。如前文所述，数值的选取取决于具体行业的统计数据，参考Lambertini和Mantovani(2009)、Hatch和Mowery(1998)、严海宁和朱劲松(2008)的研究成果得到表1的数据:

表1 数值计算的参数取值

取变量的初始值均为0.01，得到：f=0.2724，g=1.1642

结论1：厂商最优的条件下，模型的解存在一个具有稳定性的鞍点均衡。

由式(9)，代入数据后，利用matlab求解得的四个值为：

λ1=0.1000+0.5907i

λ2=0.1000+0.5907i

λ3=0.2630+0.0000i

λ4=-0.0630+0.0000i

因为只存在一个具有负实部的解，说明在此情况下，企业存在一个鞍点均衡。但是解的情况依赖于参数的选取，当参数变化时，需要代入此式求解进行稳定性的验证。

根据上文所述的过程，得到了控制变量、决策变量关于时间的完整表达式，据此画出变量路径的图像(见图1～6)：

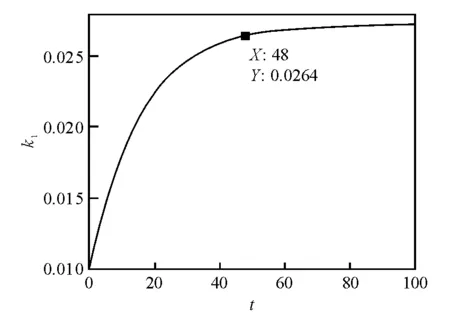
图1 产品创新最优路径

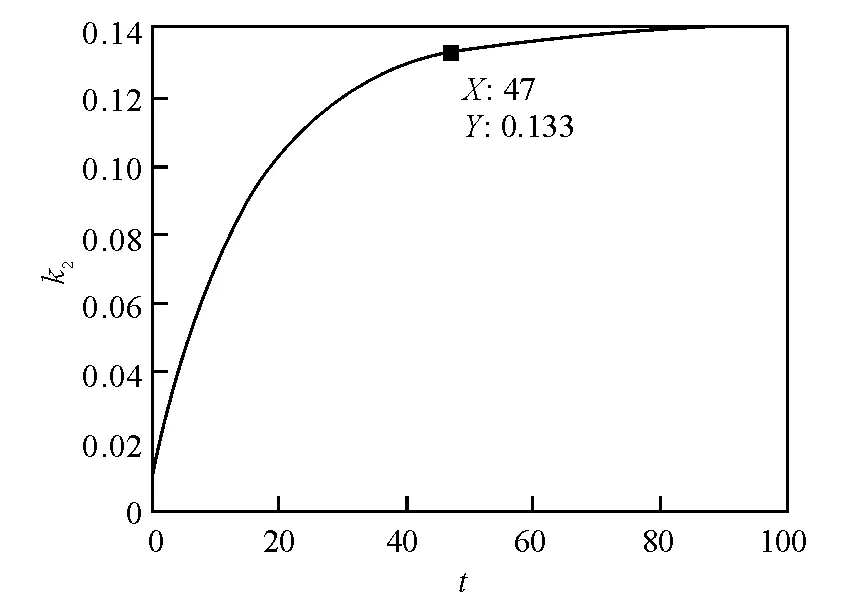
图2 过程创新最优路径

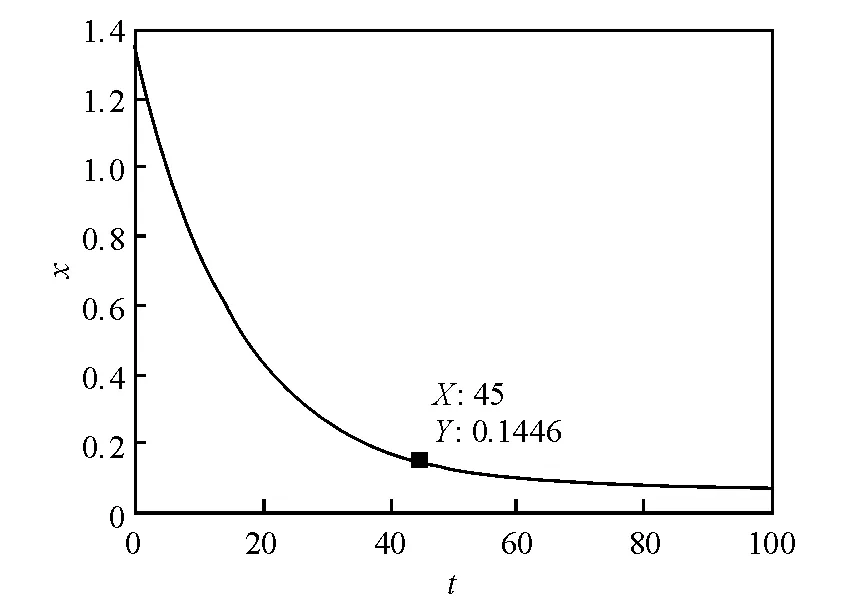
图3 产量最优路径

图4 产品价格最优路径

可以定义变量在完成95%的改变量时基本达到稳态，也就是图5中所对应的第48单位时间。

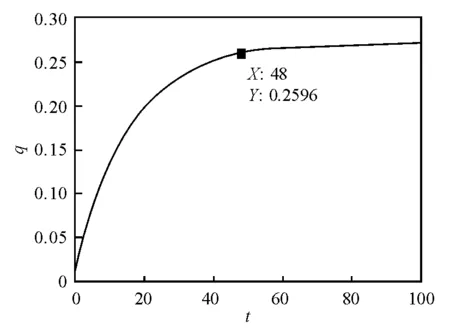
图5 产品质量最优路径

结论2：在垄断厂商最优条件下，厂商对产品创新和过程创新的投入之间存在互补关系。

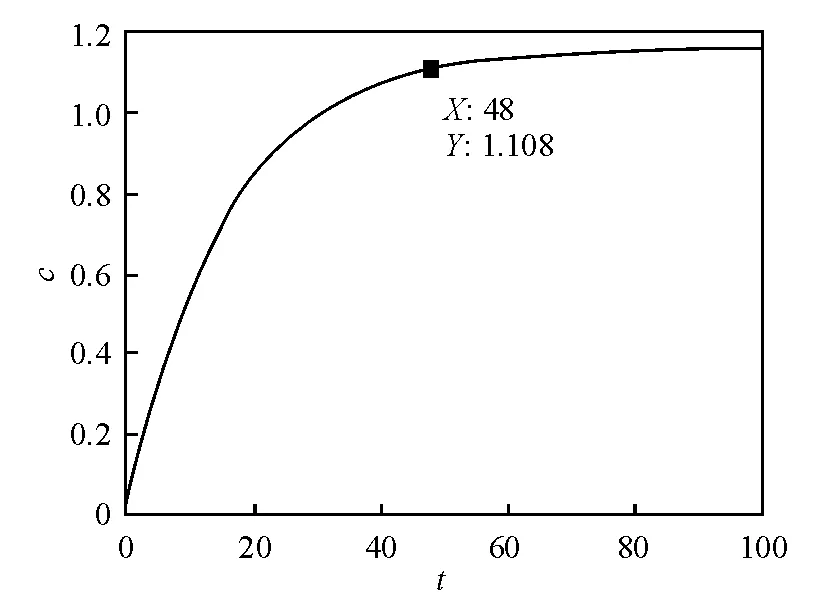
图6 产品成本最优路径

证明：将决策变量对时间求导，得

代入数据得

可以看到，产品创新和过程创新的投入均随时间而增加，即在最优决策时，随着产品创新投入的增加，需要搭配更多的过程创新，反之亦然。所以两种创新方式具有互补效应，与Mantovani(2006)的研究结果相符。进一步地，由

可知在本文的模型条件下，k1、k2的技术替代率为定值，企业对两种技术创新追加的投资是成比例的。

2 社会最优决策

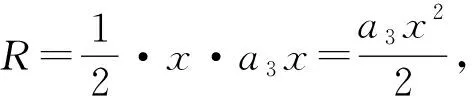
(14)

列出当期汉密尔顿函数：

(15)

沿用上节的解法，解出变量的最优路径为

(16)

λ2、f2、g2分别由式(17)～(19)决定:

ρ1λ4+ρ2λ3+ρ3λ2+ρ4λ+ρ5=0

(17)

其中：

(18)

(19)

(20)

代入数据得λ2=-0.064，f2=0.2363，g2=1.1372。

结论3：在动态的一般垄断市场情况下，社会最优和企业利益最大化具有和静态模型相同的结论，即社会最优时产品的供给量较高，价格较低，且等于生产成本。证明如下：

将式(16)中x的表达式代入需求函数，得到

p=(c0-g2)eλ2t+g2=c

(21)

即在社会最优条件下，厂商对产品的定价等于成本。代入数据，可以得到价格和产量的路径，并和厂商利润最大化做比较(见图7、8)：

图7 厂商最优和社会最优的产品数量对比

图8 厂商最优和社会最优的产品价格对比

可以看出，在社会最优条件下，产品的价格更低，产量更高，此时消费者具有更高的福利水平。这和静态一般垄断模型的结论是相同的。

3 利率和初始值对决策的影响

决策变量的表达式中折旧和比例常数等参数一般是经济的外生变量，是企业难以控制并且相对稳定的。利率不仅在很大程度上被政府作为工具来使用，而且对企业的投资决策具有重大影响，所以比较具有研究意义。在本文的模型中，利率不仅影响了企业的利润水平，同时通过影响λ的值，影响了企业达到稳态的时间：

由式(23)、(24)可求出，为保证稳态时决策变量值为正，即

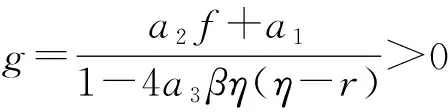
前文研究了r=0.2水平下的模型，下文通过研究r变化时企业利润最大化决策中产量和价格的变化，来说明利率对企业决策的影响。利率对企业其他决策、状态变量也有类似的影响，限于篇幅暂不做讨论。

根据式(22)作出r-λ图像：

由图9可知，在r从0.12增加的过程中，λ也单调增加，且恒为负，所以产量x和价格p的表达式为

图9 r-λ关系

结论4：随着利率绝对值的减少，到达稳态所需时间将会增加，即利率越高，企业决策调整的周期越长。

从经济学角度直观地解释，利率的增加使得投入技术创新资金的机会成本升高，企业将会降低创新力度，缓慢地革新技术。初始值对企业决策的影响，可以从变量的表达式来分析，限于篇幅，本文只讨论产品创新和过程创新的初始值对相应企业决策的影响。

由k1的表达式k1=(k10-δf)eλt+δf，可知：

结论5：当k10<δf时，k1会逐渐增加，即企业应逐步增加产品创新的投入。

这是因为产品质量“折旧效应”造成了消费者保留价格下降，它带来的利润损失大于企业“节省”的技术投入费用。此时，企业增加过程创新的投入是有利的，因为投入过程创新所带来的利润将比技术投入的费用更加可观。

同理，由k2的表达式k2=(k20-ηg)eλt+ηg，可知：

结论6：当K20<ηg时，企业应该增加过程创新的投入。

与产品创新的原理相同，这是因为过程创新的成本项(资金的机会成本)小于利润项(成本下降带来的利润上升)，所以此时企业需要增加过程创新的投资。

4 总结

本文对具有产品创新和过程创新的一般垄断市场的动态最优决策进行了求解。与已有的动态模型相比，本文的主要贡献在于研究方法上的创新。通过求解完整的动态决策路径，不仅验证了两种创新方式的互补关系，得到了和Mantovani等人相同的结论，也比较了社会福利最大化和企业利润最大化的不同决策，取得了与静态模型相同的结论，说明动态模型是静态模型更实际的推广。同时，作为应用，本文讨论了一些参数如利率和变量的初始值对企业决策的影响，这也是目前的动态研究中很少涉及的部分。本文的局限性在于所研究的一般垄断市场只是一个简化了的模型，在现实社会中并不常见。在今后的研究将着力对更符合现实的复杂市场模型进行描述和分析求解，以期得到更有价值的发现。