设施选址决策关键风险因素识别研究——以H设施为例

李鸣宇 陆云峰 马驰 高金垚

(1.航天工程大学，北京 102200；2.31697部队，辽宁 大连 116104)

0 引言

选址问题来源于不同功能设施的勘察定点和工程施工建造等具体工程项目实际背景，是合理规划空间、配置资源、发挥效能和规避风险的关键。设施选址具有很高的风险性，不合理的选址决策会限制设施效能发挥、影响空间布局，且一旦选址位置确定，短时间内很难变更，一系列不利影响会持续很长时间。因此，设施选址的风险管理尤为重要。科学、全面地判定设施选址过程中的风险因素，可通过量化、科学的方法筛选确定关键风险因素，解决原始风险因素过多、风险因素权重不明确的问题，以期用少数关键风险因素最大限度反映风险信息，为后续开展风险评估提供科学、客观的数据支撑，尽可能地降低风险的破坏性，提升风险的机会性，评估出最小消极风险的备选地址，完成设施选址决策。

1 因子分析法确定关键风险因素

1.1 因子分析法概述

因子分析法是由英国心理学家C.E.斯皮尔曼提出的一种减少变量数目、检验变量之间关系的方法，其基本思想是将原始的显性变量按照彼此的相关性分类，将相关性强的原始变量归为一类，不同类变量之间的相关性很低[1]，便于将原始的、大量的数据进行简化处理，旨在以最小的信息缺失，将大量原始数据凝聚为少数几个新概念变量，以及使新概念变量具有较强的解释性[2]。原始的各变量属于显性变量，少数几个新概念变量属于潜在变量，因此称其为因子，用于描述原始变量中具有相关性的多个变量。

1.2 确定关键风险因素步骤

根据待选位置的实际情况对其进行风险因素的全面识别，而后运用因子分析法对原始风险因素进行处理，筛选出关键风险因素，为后续风险评估提供参考。具体步骤如下。

1.2.1 统一原始风险因素表达形式

对原始风险因素进行标准化处理，并求其相关矩阵。设原始风险因素由两部分组成：公共因子和特定因子。公共因子是所有原始变量共同拥有的因子，能够解释原始风险因素之间的关系；特定因子是该风险因素本身特有的因子，不能被公共因子所阐释。

假设待选位置中有q个原始风险因素r=(r1，r2，…，rq)′，均值是μ=(μ1，μ2，…，μq)，协差阵是∑=(σij)，原始风险因素的因子模型为

r1=μ1+a11f1+a12f2+…+a1mfm+ε1

r2=μ2+a21f1+a22f2+…+a2mfm+ε2

…

rq=μq+aq1f1+aq2f2+…+aqmfm+εq

其中，f1，f2，…，fm是公共因子，是原始风险因素都包含的因子。ε1，ε2，…，εm是特定因子，是各原始风险因素各自特有的因子。公共因子和特定因子皆为不可观测的变量，上式可以通过矩阵表示

r=μ+Af+ε

式中，f=(f1，f2，…，fm)′是公共因子向量，ε=(ε1，ε2，…，εq)′是特定因子向量;A=(aij):q×m为因子载荷矩阵。

假定

E(f)=0

E(ε)=0

V(f)=I

V(ε)=D=diag(σ12，σ22，…，σq2)

Cov(f，ε)=E(fε′)=0

各公共因子之间不相关，同时具有单位方差，各特定因子之间不相关且和公共因子也不相关。

1.2.2 分析原始风险因素之间的相关性，验证运用因子分析法适合与否

当原始风险因素满足两个条件时，说明适合进行因子分析：

(1)巴特利特球体检验，显著性值<0.01。

(2)KMO检验，KMO值>0.5。

KMO检验用于计算原始风险因素之间的简单相关系数和偏相关系数，其数学表达式为

KMO的值越大，越适合采用因子分析的方法，其标准为：>0.9,非常适合；0.8～0.9适合,0.7～0.8,一般适合；0.5～0.7，不太适合，比较勉强；<0.5，不适合。两种检验方法均可运用SPSS软件进行验证。

1.2.3 提取公共因子，选择合适的公共因子的数量表达原始风险因素信息

1.2.4 进行因子旋转，使公共因子对原始风险因素具有较强的解释能力

因子解释起来带有主观性，可通过因子旋转促成原始风险因素的分类，减少主观性使公共因子易于解释，这一过程能否适用关键在于因子载荷矩阵A的元素结构。假设A是从R出发求得的，则有|aij|≤1，如果矩阵A中所有的元素都接近0或±1，那么模型因子就易于解释。此时将r1，r2，…，rq分为m个部分，分别对应f1，f2，…，fm，称其为简单结构。

正交旋转：f*=T′f，相应地有A*=AT，记

A′=(a1，a2，…，aq)，A*′=(a1*，a2*，a3*，…，aq*)

因A*′=T′A′，即

(a1*，a2*，…，aq*)=T′(a1，a2，…，aq)ai1*

故ai*=T′a(i=1，2，…，q)

对m=2时的一般情况，假设按照逆时针旋转的角度为θ(如果是负数，则为顺时针)，则旋转前后的因子载荷有如下关系式

当因子数m>2时，运用最大方差旋转法，令

若A*=(a*ij)，则A*的第j列元素平方的相对方差可以定义为

选择正交矩阵T，使得m个列元素平方的相对方差之和V=V1+V2+…+Vm达到最大。

1.2.5 对公共因子进行定义

根据原始风险因素的分类情况，对公共因子所表示的类别进行重新定义和命名。

1.2.6 计算各因子得分，对结果进行解释

公共因子能够反映出原始风险因素之间的相关关系，采用公共因子作为原始风险因素的代表时，更加有利于对研究对象的特征进行描述。因此，可以将公共因子用原始风险因素的线性组合形式表示

fj=bj1r1+bj2r2+… +bjqrq(j=1，2，…，m)

称f为因子得分函数，用来计算因子得分，进而进行后续统计分析。

rj的因子得分可用回归法计算，如下

2 实例分析

2.1 项目概况

H设施是为了实现天然气钻探的地质目标所建设的钻前工程，是为油气勘探开发提供设备基础、进场道路、钻井场地、池类以及供电、供水等的临时工程，是钻井工程顺利实施的保障。由于地理、水文和人文方面选址的制约因素多，选址决策比较困难。

2.2 确定原始风险因素

H设施现有3个待选位置，通过查阅相关资料和整理专家的意见建议[3-7]，初步识别出4类共9个原始风险因素，见表1。

表1 H设施待选位置原始风险因素清单

2.3 因子分析法筛选确定关键风险因素

采用专家评分法对地质、水文和油气勘探领域150名经验丰富的专家进行问卷调查，给上述原始风险因素对待选地址决策的影响程度进行打分。打分规则：“风险巨大”计9分；“风险较大”计7分；“风险一般”计5分；“风险较小”计3分；“风险可忽略不计”计1分。发放问卷150份，回收问卷116份，有效问卷108份，有效问卷率为93.1%。运用SPSS软件对原始风险因素问卷进行分析：

KMO值为0.816，适合；Bartlett检验的显著性0.000<0.01，说明原始风险因素之间存在相关性，可以运用因子分析法进行问题研究。表2为KMO和Bartlett检验值。

表2 KMO和Bartlett检验值

通过公因子方差的值体现对公共因子的解释能力，除了滑坡R1和洪水灾害R7的公因子方差较小，其余风险因素的公因子方差值均在0.75以上，说明公因子整体上对原始风险因素的解释能力较强，滑坡R1和洪水灾害R7公因子方差<0.4，予以剔除。公因子方差值见表3。

表3 公因子方差值

在主成分分析法的基础上，选取特征根>1的因子，通过主成分因子的特征值和方差贡献度可以看出，因子1～3的特征值>1，原始风险因素可以提取为3个公共因子，这3个公共因子可以解释86.747%的信息，且公共因子负荷系数绝对值高，说明原始风险因素相关性显著。总方差解释见表4。

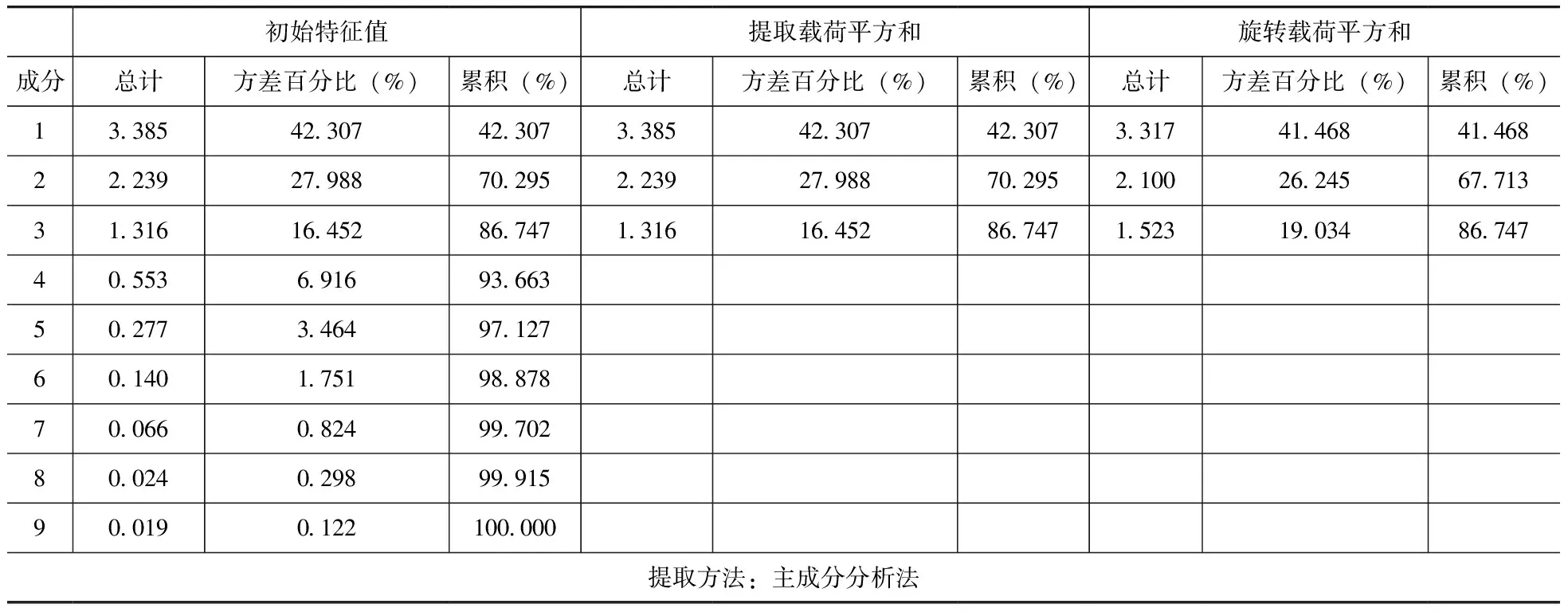
表4 总方差解释

通过表5确定公因子中的关键风险因子及公因子所代表的风险。第一个公因子贡献率为36.463%，负荷系数在钻前工程活动、钻井(试油)作业、后期油气开发生产三个风险因素上分别是0.902、0.881、0.713，负荷系数较高，且与环境危害风险相对应，表明了环境风险对该项目选址决策的影响；第二个公因子贡献率为24.807%，负荷系数在矿井(坑道)风险和溶洞风险上为0.835和0.828，这两个风险因素对应矿井(坑道)、溶洞危害风险；第三个公因子贡献率为16.493%，负荷系数在泥石流和岩石崩塌上分别为0.894、0.791，这两个风险因素与地质灾害风险相对应。表6进一步总结了H设施待选地址风险因素的公因子及其贡献率和构成公因子的主要风险因子指标。

表5 旋转后的成分矩阵

表6 公共因子及其贡献率

确定公因子在H设施选址风险中的所占因子权重。因子权重为因子贡献率和因子累计贡献率的比值。从表7可以看出，该设施选址决策项目受环境危害风险的影响最大，其因子权重达到46.890%；其次是矿井(坑道)、溶洞危害风险，因子权重为31.901%；再次是地质灾害风险，因子权重为21.209%。

表7 因子权重

通过因子分析法，剔除H设施待选地址中滑坡和洪水灾害两个非关键风险因素，确定H设施待选地址风险因素按照重要程度从高到低为：环境危害风险>矿井(坑道)和溶洞危害风险>地质灾害风险，可为后续风险评估提供科学依据和参考。

3 结语

对待选位置的风险因素进行科学识别和评价，是有效风险评估和后期设施建设运营的前提。本文提出运用因子分析法对设施选址决策进行风险识别，并以H设施选址项目为例，采用问卷调查的方法咨询专家，结合文献资料查阅结果，运用因子分析法对原始风险因素进行分析处理，筛选并确定关键风险因素及其排序，旨在提高设施选址风险识别能力，具有一定的实践价值。需要注意的是，在运用因子分析法时，需要有足够的样本量作为数据支撑，样本数要大于100份，样本数应为原始变量数的5倍以上，否则将出现因子分析结果不稳定、缺乏说服力等情况。