基于多传感器信息融合的车辆高精度定位技术

师小波 赵丁选 孔志飞 倪 涛 赵小龙 郭庆贺

1.燕山大学电气工程学院，秦皇岛，0660042.燕山大学机械工程学院，秦皇岛，0660043.燕山大学车辆与能源学院，秦皇岛，0660044.河北建材职业技术学院，秦皇岛，0660045.吉林大学机械与航空航天工程学院，长春，130022

0 引言

我国幅员辽阔、人口众多，自然灾害时有发生，高机动应急救援车辆作为救援装备，需要在复杂的道路环境下保持良好的驾驶平顺性和操纵稳定行，以确保车辆快速安全地到达灾害现场。基于车前地形的主动悬挂控制方法通过车辆地形建构系统和组合导航系统来调节主动悬架作动力，以保证车辆在复杂的道路冲击下仍能具有较高的平顺性和稳定性。实现上述悬架控制方法需要车辆在复杂地形环境中的高精度定位技术。

近年来，全球定位系统(global positional system，GPS)以其定位精度高、速度快等优势得到了广泛应用，但其信号不稳定、频率低，当处于有楼房遮挡或者信号反射严重的环境时很难精确定位。

目前，室外定位技术[1-4]已有诸多研究成果，依据获取数据的传感器的不同主要分为如下三类：基于航迹推算(dead reckoning，DR)的室外定位技术，基于卫星定位的室外定位技术，基于环境感知的室外定位技术。但在复杂的室外环境下，单一的定位方法难以满足实际需求，随着多传感器信息融合技术的日益成熟和完善，人们考虑通过融合多个传感器采集的数据，以实现一个更为精确和稳定的室外定位系统[5-8]。文献[9]提出了一种基于全球导航卫星系统(glabal navigation satellite system，GNSS)、惯性测量单元(inertial measurement unit，IMU)、视觉多传感器融合的组合定位系统，可同时克服单一传感器的定位缺陷；文献[10]提出的长距离GPS、北斗卫星导航系统(BeiDou navigation satellite system，BDS)网络实时动态(real-time kinematic，RTK)定位方法可实现GPS/BDS单系统、双系统的厘米级定位；文献[11]提出的激光雷达测程和测图(lidar odometry and mapping，LOAM)算法实现了IMU、视觉、激光三种传感器数据的融合，是目前公认的精度最高的定位算法，但在缺少特征点的环境中难以实现车辆的准确定位。上述方法试图通过融合多个传感器构成组合定位系统来消除单一定位方法的局限性，虽然定位精度和稳定性有了很大提高，但也同时存在着某些缺点。

现有的高精度定位技术主要面向无人驾驶领域，使用场景大多在城市和高速公路等二维平面内，无法满足应急救援车辆的高精度定位需求。此外，相比于城市场景下的无人驾驶乘用车辆，多轴应急救援车辆需要在复杂的道路环境下行驶，面临着GPS信号频繁丢失、受阻等问题，无法保证行驶过程中的稳定性。

基于上述分析，本文在研究现有室外定位技术的基础上，通过融合GPS、IMU、激光雷达信号，实现实时、稳定、准确的信号输出，满足多轴应急救援车辆在复杂道路环境下高精度、高稳定性的定位需求。

1 总体方案设计

本文以三轴越野车辆为载体，GPS、IMU、VLP-16为硬件设备，实现车辆定位和环境感知功能。系统总体方案如图1所示，选用GPS、IMU作为前端里程计[12]模型所使用的传感器，通过卡尔曼(Kalman)滤波器[13-16]实现两者的数据融合。融合后计算的车体位姿信息既能够克服GPS信号不稳定、获取数据效率低的问题，又能够同时解决IMU定位带来的累积误差问题。后端优化模型[17]首先使用VLP-16激光雷达获取车体周围点云信息[18]，然后构建全局地图以及局部高程地图，通过局部和全局地图特征点云匹配，实现对前端里程计模型的误差修正。

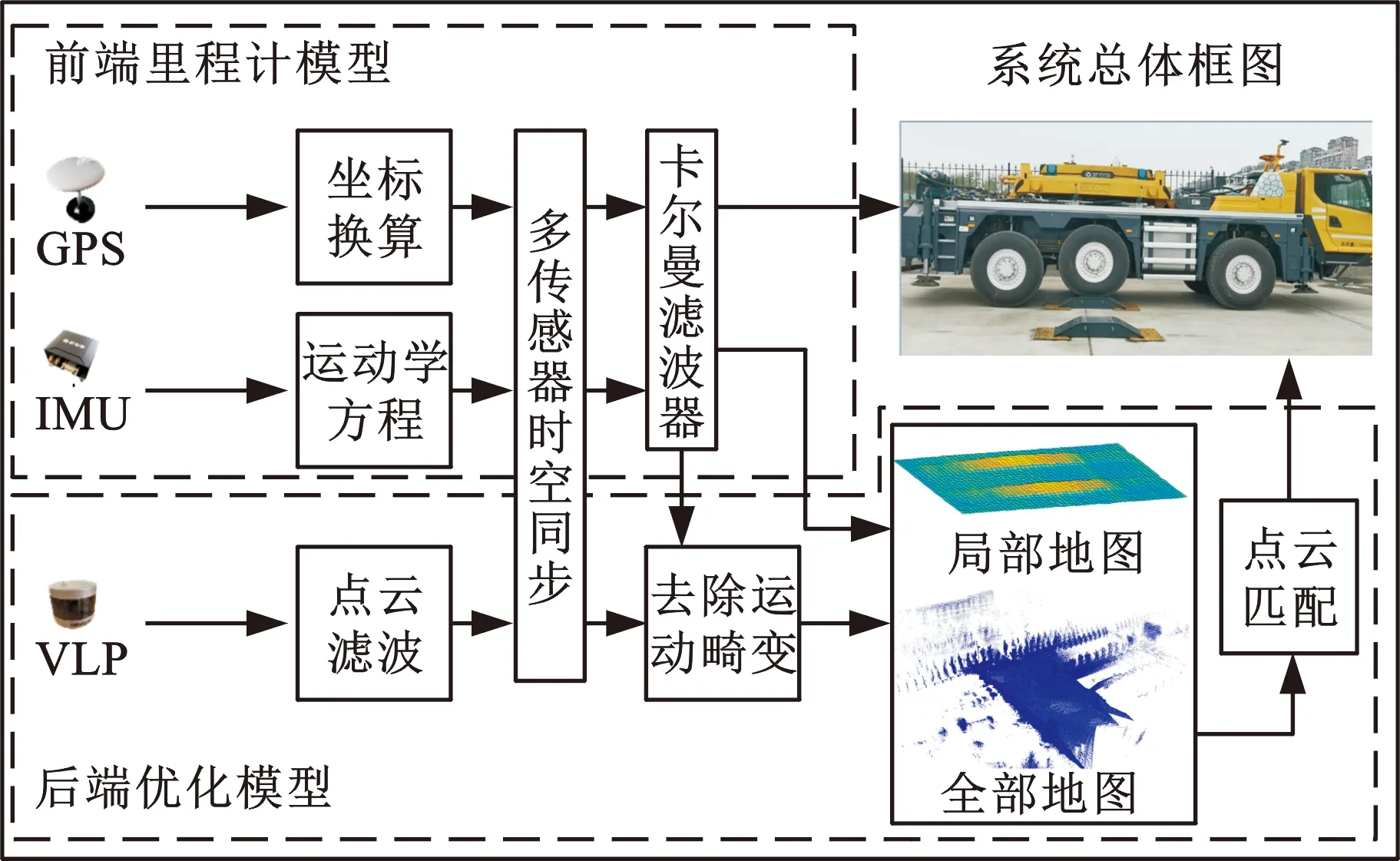
图1 总体方案示意图Fig.1 Schematic diagram of the overall plan

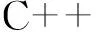
2 前端里程计模型的构建

2.1 基于IMU的运动学预测模型

考虑到三轴车复杂的结构特点和动力学特性，本文首先建立了三轴车辆运动学模型[19]，如图2所示。L1，2为第一、二轴轴距，L2，3为第二、三轴轴距，P为转向中心，R为车辆转向半径，δf、δr分别为车辆前轮和后轮的转向角，(Xf，Yf)、(X，Y)、(Xr，Yr)分别为车辆第一、二、三轴的轴心坐标，θ为车辆纵轴线与环境坐标系横轴的夹角(即车辆的航向角)。

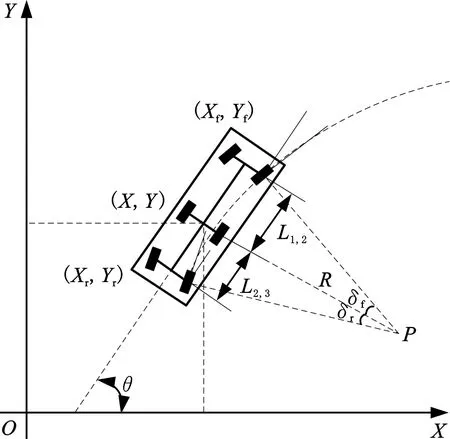
图2 三轴车运动学模型Fig.2 Three-axis vehicle kinematics model

车辆的运动学微分方程如下：

(1)

式中，st为车体的位置向量；vt为车体的速度向量；at为车体的加速度向量；qt为四元数；ωt为车体角速度向量；abt为加速度畸变；ωbt为角速度畸变；gt为重力加速度；aw、ωw分别为从感器获取的加速度向量、角速度向量；下标t表示t时刻。

通过IMU获取的数据存在误差，所以需要将式(1)推导为包含IMU测量噪声的运动学微分方程：

(2)

式中，s为IMU获取的位置向量；v为IMU获取的速度向量；q为通过IMU数据转化的四元数；ωb为IMU获取的角速度向量；ab为IMU获取的加速度向量；g为重力加速度；δ为对应量的测量误差。

车体运动速度与IMU取得的加速度存在如下约束关系：

(3)

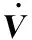
式(1)构建的运动学微分方程难以求解，本文将时间离散化，在Δt时间内，根据车体由k-1到k时刻的状态转移构建系统的误差状态预测方程。

通过IMU数据构建的运动学差分方程如下：

(4)

式中，vk-1、sk-1、ab，k-1、ωb，k-1、qk-1分别为k-1时刻通过IMU获取的速度、位置、加速度、角速度和四元数值；vk、sk、ab，k、ωb，k、qk分别为k时刻通过IMU获取的速度、位置、加速度、角速度和四元数值。

IMU测量误差构建的运动学差分方程如下：

(5)

式中，vi、θi分别为速度、姿态角的测量误差；ab，i、ωb，i分别为加速度、角速度的测量畸变。

2.2 基于GPS的运动学预测模型

通过IMU获取的车辆位姿信息存在累积误差，本文选取GPS定位系统，通过GPS与IMU的信息融合算法去消除累计误差，提高定位系统精度。

通过GPS获取的全局坐标与IMU积分获取的定位坐标换算关系如下：

gm=hx(xm)+λ

(6)

式中，gm为GPS观测到的定位坐标；xm为IMU获取的定位坐标；hx(·)为IMU与GPS数据之间的转化函数；λ为GPS的位置测量误差。

由式(6)可得到位置误差状态观测方程和位置误差状态协方差矩阵：

δgm=HPδxm

(7)

(8)

式中，Hp为位置雅可比矩阵，通过hx(·)对δxm求导获取；U为GPS测量误差的协方差矩阵。

通过GPS获取的偏航角与IMU积分获取的偏航角存在如下的换算关系：

θm=hθ(xm)+θz

(9)

式中，θm为GPS获取的偏航角；hθ(·)为IMU和GPS航偏角信息之间的换算函数；θz为GPS的测量误差。

由式(9)可得到偏航角误差状态观测方程和偏航角误差状态的协方差矩阵：

δθm=Hθδxm

(10)

(11)

式中，Hθ为偏航角雅可比矩阵，通过hθ(·)对δxm求导得到；Θz为协方差矩阵。

通过GPS获取的车体速度与IMU积分获取的速度关系如下：

vm=hv(xm)+vz

(12)

式中，vm为GPS获取的速度；hv(·)为IMU与GPS速度信息的换算方程；vz为GPS的速度测量误差。

由式(12)可得到速度误差状态观测方程和速度误差状态的协方差矩阵：

δvm=Hvδxm

(13)

(14)

式中，Hv为速度雅可比矩阵，是hv(·)对δxm的导数；Vz为速度协方差矩阵。

2.3 状态更新

本文以卡尔曼滤波器为模型框架，通过卡尔曼增益矩阵修正误差状态，实现IMU和GPS数据融合，更新系统状态和系统协方差矩阵。

卡尔曼增益矩阵如下：

(15)

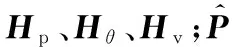
通过卡尔曼增益取修正误差状态，修正后的误差状态方程为

(16)

更新后的系统协方差矩阵为

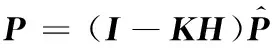
(17)

式中，I为单位矩阵。

3 后端模型优化

3.1 方案设计

前端里程计可以输出车体的位置信息，但其定位精度仍无法满足实际场景下所需的要求，为解决这一问题，本文采用点云匹配算法对前端里程计获得的车辆位姿信息进行优化，并构建后端优化模型，其算法流程如图3所示。

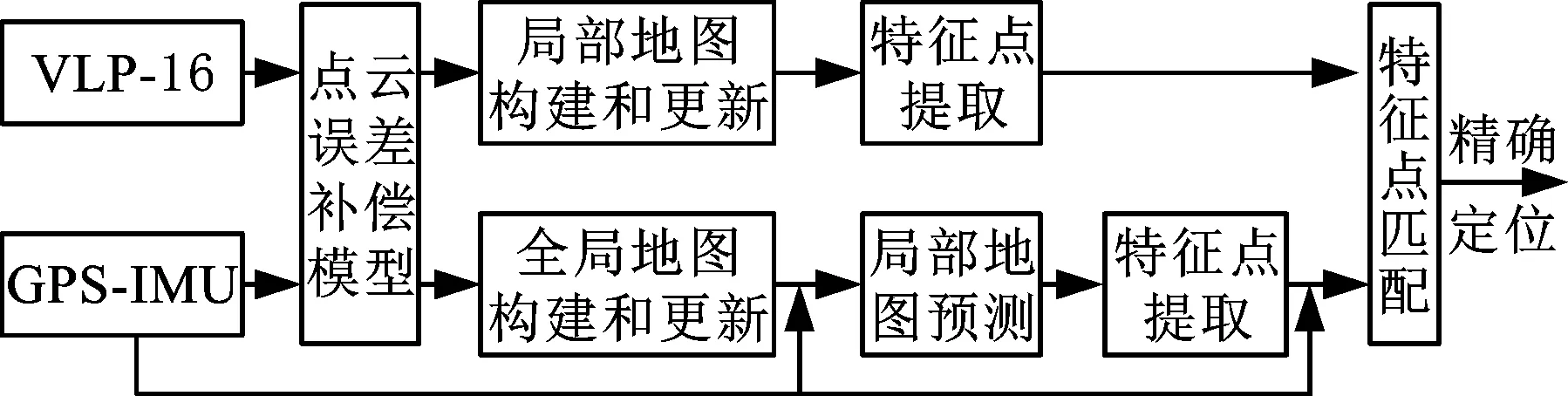
图3 基于特征点云匹配的后端优化模型算法流程图Fig.3 Algorithm flow chart of back-end optimization model based on feature point cloud matching

3.2 点云误差补偿

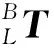
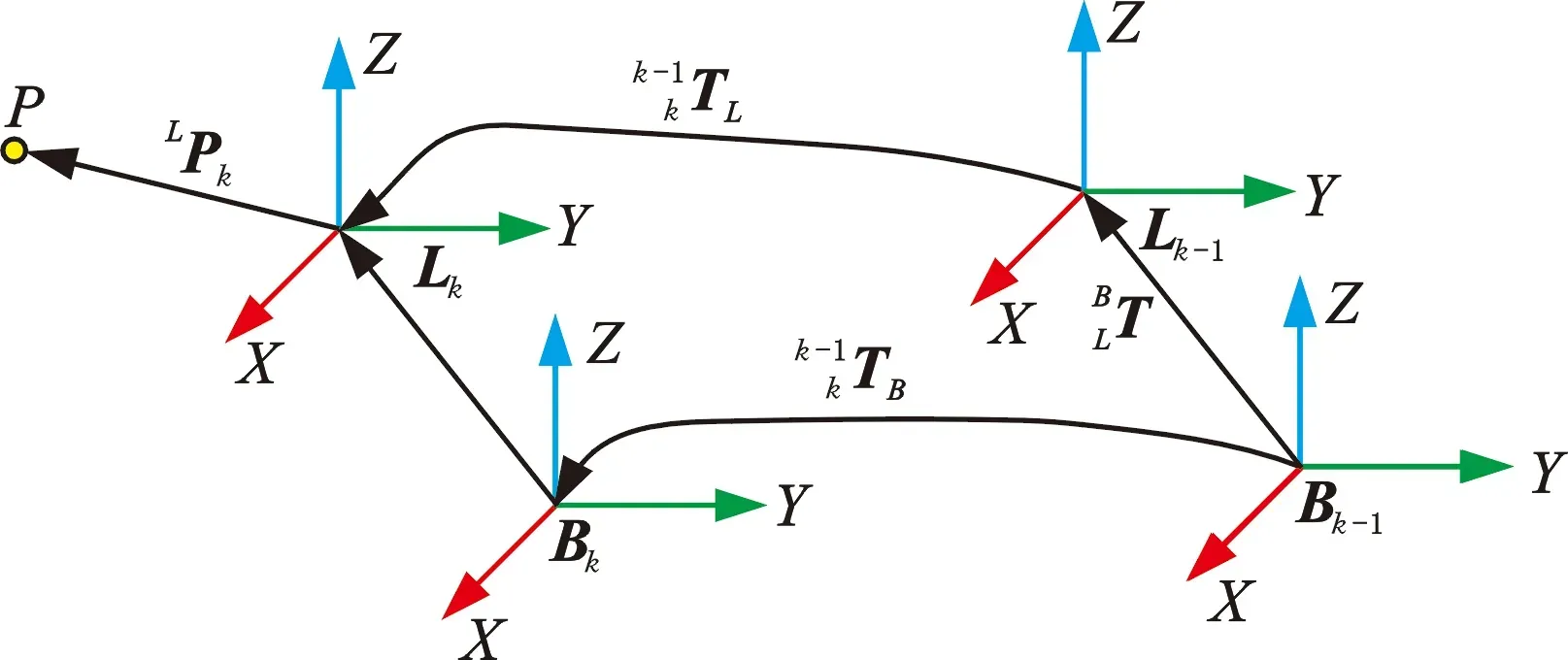
图4 外参标定求解示意图Fig.4 Schematic diagram of external parameter calibration solution

点P在世界坐标系下的坐标可以通过两种方法求解：

一是通过前端里程计模型计算点P在k时刻的坐标WPk：

(18)

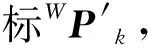
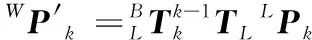
(19)

结合式(18)、式(19)构建优化方程：

(20)

3.3 构建特征点云匹配模型

为了提高车体定位过程中点云匹配算法的效率以及精确度，对点云数据集中的点进行了分类，如图5所示。

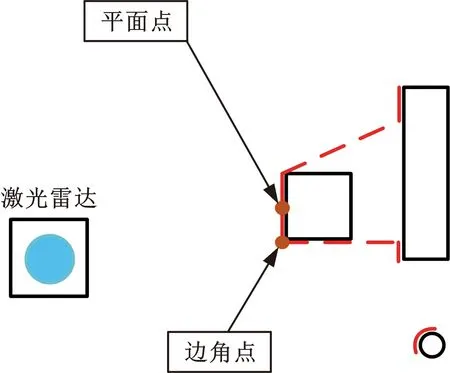
图5 特征点分类示意图Fig.5 Feature point classification diagram

本文将点云分为平面点和边线点两类，并对采集到的每一个点求其特征值c，其计算公式如下：

(21)

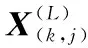
按照曲率对特征点进行分类时会存在两类无效特征点：一是由于相邻点与激光雷达之间的夹角过小而形成的无效特征点；二是由于某些障碍物的遮挡而形成的无效特征点。为了保证选取特征点的有效性，本文将每根扫描线平均划分为6个区间，在每个区间内，按照点云曲率的大小进行排列，选取曲率较小的4个点作为平面特征点，选取曲率较大的2个点作为边角特征点。

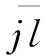
(22)

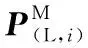
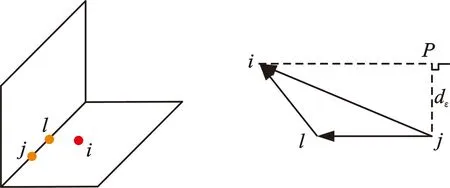
(a)边线特征点 (b)几何关系图6 边线特征点求解示意图Fig.6 Schematic diagram of solving edge feature points

平面特征点的求解如图7所示，点i为局部地图上的平面特征点，点j、l、m分别为全局地图上距离点i最近的三个点，则点i到平面jlm的距离为

(23)

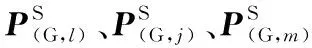
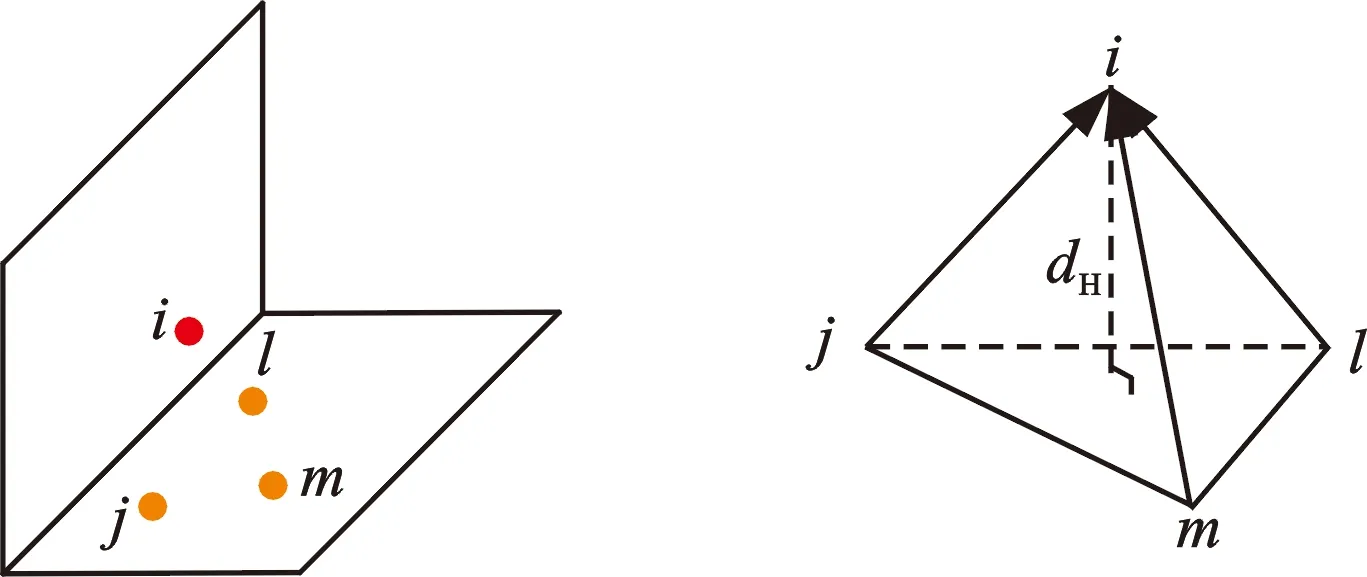
(a)平面特征点 (b)几何关系图7 平面特征点求解示意图Fig.7 Schematic diagram of solving plane feature points

全局地图与局部地图坐标系下的平面特征点存在以下关系：

(24)

全局地图与局部地图坐标系下的直线特征点存在以下关系：

(25)

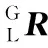
联立式(21)～式(23)得

(26)

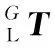
4 实验及数据分析

本文在真实环境中对定位系统进行了精度和稳定性实验，通过对比算法处理的数据和真实测量的数据来验证系统定位的准确性和稳定性。实验车辆参数如表1所示。

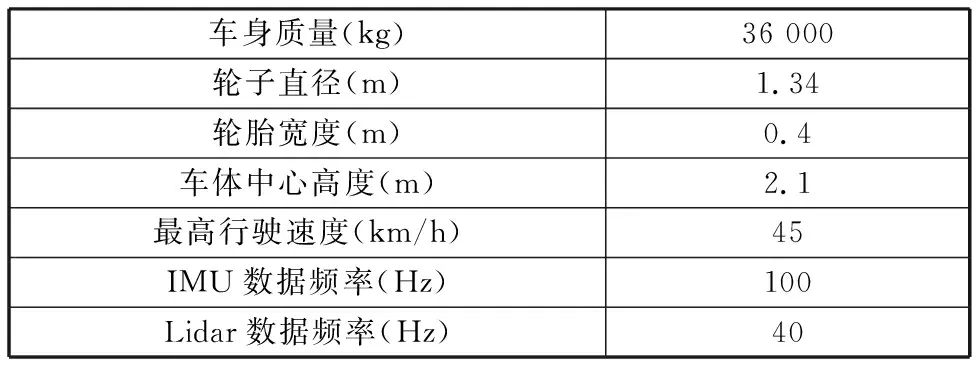
表1 车辆参数

实验过程如下：车体在室外沿直线运行，在其运行轨迹上设置双边桥路障，如图8所示。车体行进过程中选取12个点进行测量。车体在通过双边桥的过程中通过车载传感器实时收集数据并绘制出高度(z)变化曲线和俯仰角的变化曲线(图9)，通过对比真实测量的垂向高度数值和俯仰数值来验证定位系统的精度。

图8 双边桥路障Fig.8 Bilateral bridge obstecles

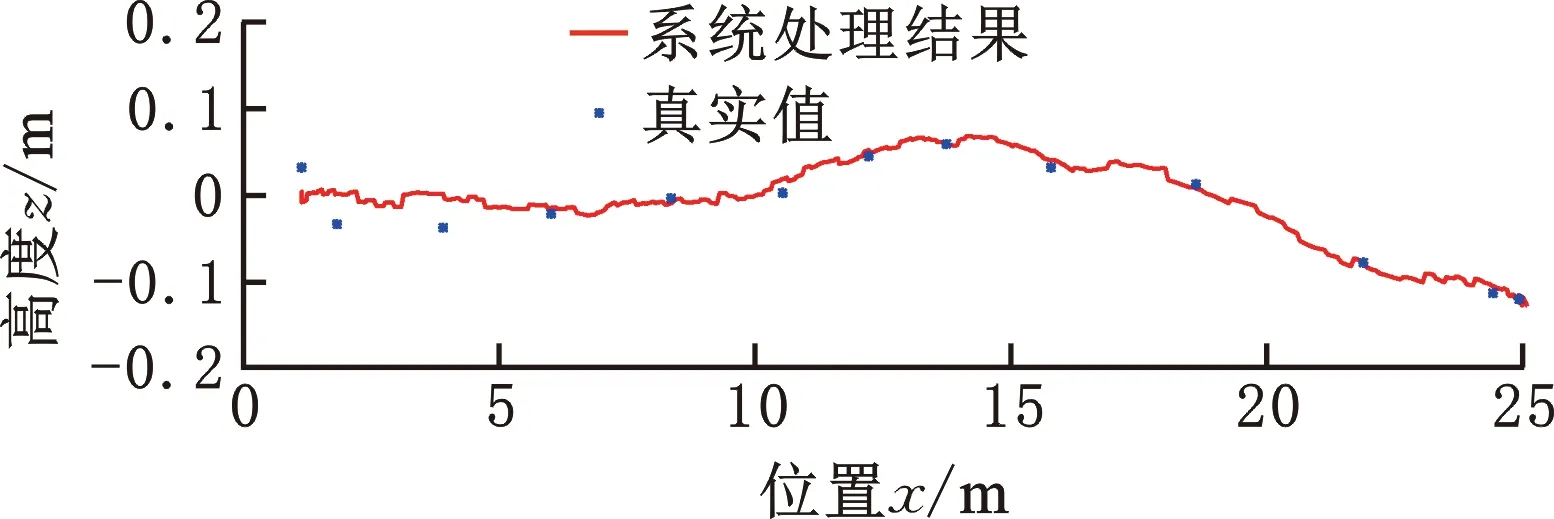
(a)高度变化曲线

系统输出结果与真实测量值之间的均方根误差即为系统的定位精度，通过图9的数据计算可得系统的定位误差为3.45 cm，角度误差为0.10°。

通过屏蔽部分时间段的GPS信号来获得GPS不稳定时段的定位数据，对比GPS信号稳定和GPS信号不稳定的实验数据，以验证定位系统的稳定性。同时，将本文提出的算法与LOAM算法进行对比，以验证系统在缺少特征点环境中的稳定性，绘制数据对比曲线如图10所示。

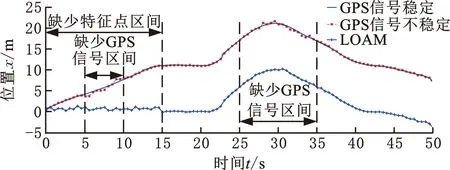
(a)x方向上轨迹对比

通过图10曲线可以看出，当GPS信号不稳定时，车辆的定位精度会降低，GPS信号恢复后，车辆定位系统会迅速回到稳定状态；通过对比LOAM算法可知，LOAM算法在缺少特征点的环境中难以进行精准的定位，而本文提出的算法可以有效地优化此类问题。

为了进一步验证算法的实时性，使车辆以恒定速度多次通过障碍物，并实时记录本文提出的算法与LOAM算法的程序运行周期，相关程序在2.5 GHz四核处理器和6 GB内存的Win10操作系统上运行，数据对比如表2所示。

通过表2可知，LOAM算法的平均运行周期为120.6 ms，而本文提出的算法平均运行周期为85.6 ms，所以在实时性方面可以满足高机动救援车辆的需求。

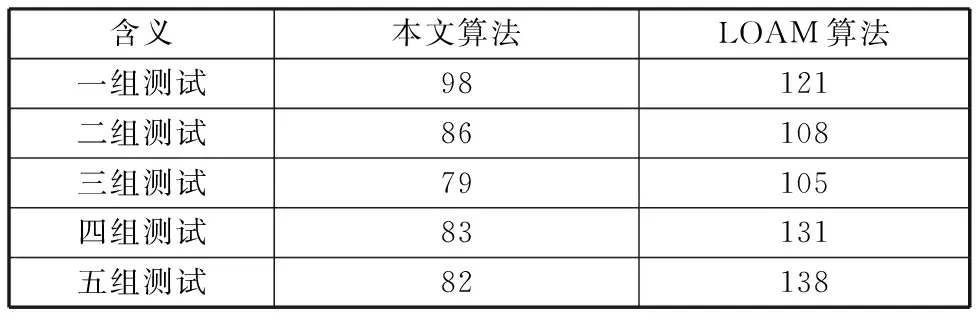
表2 算法数据

5 结语

本文提出了一种基于多信息融合的车辆高精度定位方法，综合利用了多种传感器的优点，不仅消除了IMU的累计误差，也解决了GPS在实际环境中信号不稳定、信号丢失等问题。实车测试结果表明，在GPS信号不稳定时，提出的车辆定位方法所得到的定位误差为±3.45 cm,角度误差为±0.10°。实验结果表明该定位系统的准确性、稳定性均得到了有效改善。