基于增材制造各向异性的强度约束拓扑优化

何智成 杨丁丁 姜 潮 伍 毅 江和昕

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

目前，随着航空航天、汽车等高端装备领域的发展，设计中应用优化手段特别是拓扑优化技术的需求越来越强烈[1]。与此同时，增材制造技术的发展与其所具有的超高制造自由度特点，极大程度上推动了拓扑优化在复杂关键零部件设计中的应用[2-4]。然而，增材制造工艺因其沿路径逐层堆叠材料的物理特性，不可避免地会使制造结构具有各方向不同的力学特性[5-7]，传统基于各向同性假设的设计方法将不再适用。特别是当面对实际的复杂应用工况环境时，如果设计中缺乏对增材制造关键零部件失效强度的有效考量，其结构服役的安全性与可靠性将受到极大挑战。因此，研究考虑增材制造工艺影响的强度优化设计方法具有重要的实际价值与指导意义。

结构的断裂、疲劳、塑性变形等失效问题大多由局部应力集中引起，所以为了将优化方法推广到强度设计中，已经发展了许多以结构应力为约束或目标的拓扑优化方法。YANG等[8]与DUYSINX等[9]在早期的连续体结构应力拓扑优化研究中阐明了其面临的三个主要难点：一是应力的“奇异”现象；二是应力的局部性导致的约束数量庞大；三是计算非线性程度高。为解决这些问题，ε松弛与qp松弛方法[10-11]、全局应力聚合法(如P聚合、KS聚合函数)[8，12]、分区应力聚合[13]和改进的过滤与平均策略被相继提出，并取得了显著的效果。

目前，大多数应力拓扑优化研究都基于固体各向同性材料惩罚法(solid isotropic material with penalization，SIMP)[11-13]与水平集方法(level set method，LSM)[14-15]展开，并且它们的有效性已经在各种应用场景中得以证明。近几年，双向渐进结构优化方法(bi-directional evolutionary structural optimization，BESO)也逐渐被应用于解决应力拓扑优化问题。XIA等[16]、FAN等[17]基于BESO方法提出了一系列有效求解应力拓扑优化问题的新框架；王选等[18]改进了BESO方法以有效降低其处理应力约束问题时产生的震荡现象。值得注意的是，与SIMP法相比，BESO法与LSM法由于没有中间密度单元的概念，本身就具备避免应力“奇异”现象的潜力，但LSM法由于对初始设计较为依赖，容易受到一定限制[19]。因此基于BESO方法展开应力相关的拓扑优化研究具有很大的潜力。

尽管现有的应力拓扑优化工作能有效处理大部分涉及强度的优化问题，但这些研究几乎均基于各向同性的材料假设。近年来，针对增材制造工艺下的各向异性拓扑优化问题，已经有部分学者从不同角度开展了一些研究工作。CHIU等[20]研究了刚度各向异性与角度对优化结构最小化体积的影响。YANG等[5]基于光固化(Stereolithography，SLA)增材制造工艺下的材料试验实现了各向异性的刚度优化设计。YU等[21]在材料各向异性和沉积角度的基础上，实现了打印沉积路径规划与结构优化的并行设计。MIRZENDEHDEL等[22]提出了一种基于LSM的增材制造各向异性强度优化设计方法，并通过实验验证了方法的有效性。LI等[23]、WU等[24]针对增材制造结构的各向异性断裂行为，开发了一种增强结构抗弹塑性断裂的拓扑优化方法。除此之外，诸如多材料多打印方向优化、各向异性点阵结构优化等[25]也得到了广泛关注。

然而这些针对增材制造各向异性的研究大部分只考虑了结构的整体刚度性能，而对强度相关问题的必要关注非常有限。因此，本文在BESO方法基础上提出了一种考虑各向异性强度约束的拓扑优化方法。基于Tsai-Hill失效准则详细推导了描述各向异性结构偏轴(考虑材料堆叠角度改变)强度性能的Tsai-Hill失效系数，并通过权重因子α将失效系数约束引入拓扑优化模型。详细推导了其优化灵敏度公式，引入归一化、敏度与密度过滤等一系列数值方法稳定优化历程。最后基于两个典型算例验证算法的有效性，探讨各向异性的影响规律。

1 各向异性失效分析

1.1 Tsai-Hill失效准则

为使优化结果更贴近设计目标，使用各向异性Tsai-Hill失效准则以更准确地评估结构的失效风险。该准则已被证明在描述增材制造结构的各向异性力学性能方面是非常有效的[26-27]，本文只讨论平面应力问题，表达式如下：

(1)

其中，F.I.=1表示失效临界状态，Fij为材料强度系数，σ1、σ2分别为材料坐标系下1方向与2方向的主应力分量，τ12为切应力。材料坐标系O′12与自然坐标系Oxy如图1所示。F11、F22、F12、F66可通过下式计算：

(2)

图1 正交各向异性材料坐标系Fig.1 Orthotropic material coordinate systems

图2展示了平面应力问题下Tsai-Hill准则的失效空间(图2a)与失效面(图2b)。失效空间是由满足准则的强度极限所围成的封闭区域，为保证优化结构不失效，需使所有单元应力被约束其中。失效面为图2b所示的椭圆，是失效空间在τ12=0平面(即主应力平面)的投影，面内包络单元主应力。失效面与σ1轴交点为强度极限X1，与σ2轴交点为X2。通过失效面与单元应力的分布可简单直观地描述结构的应力状态和失效风险。

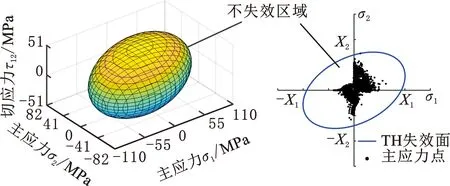
(a)Tsai-Hill失效空间 (b)Tsai-Hill失效面图2 Tsai-Hill失效空间与失效面Fig.2 Tsai-Hill failure space and failure surface

1.2 Tsai-Hill准则的坐标变换

在增材制造工艺下，材料堆叠方向会随着结构的不同而做出相应调整，使得材料坐标系与自然坐标系之间产生一定的偏转角θ，如图1所示。因此增材制造结构沿xOy坐标轴方向的强度极限(即偏轴强度极限)会随着堆叠角θ的偏转而发生改变，此时式(1)将不再适用，因此需进行坐标变换以获取考虑堆叠角的Tsai-Hill准则表达式。令

m=cosθ，n=sinθ

(3)

则σx、σy、τxy与σ1、σ2、τ12之间的关系为

(4)

式中，σx、σy、τxy为自然坐标系Oxy下的应力分量。

将式(4)代入式(1)求得Tsai-Hill准则在Oxy坐标系下的表达式：

2Fxsσxτxy+2Fysσyτxy=1

(5)

其中，Fxx、Fyy、Fxy、Fss、Fxs、Fys(下标s表示剪切方向)为自然坐标系下的强度系数，可由下式计算：

(6)

式(5)可重写为

(7)

(8)

式中，ITH为Oxy坐标系下的强度系数矩阵；σe为单元应力状态向量。

1.3 失效系数计算

将式(7)改写为如下方程：

(9)

其中，sTH定义为Tsai-Hill准则的安全系数[28]，sTH≥1表示结构不失效。为了更好地评估结构的失效风险，定义失效系数ϖTH满足

(10)

分析式(10)可知，ϖTH≤1代表结构不失效。

2 各向异性强度约束拓扑优化模型

2.1 优化模型

针对考虑各向异性的强度拓扑优化问题，需保证结构中最大Tsai-Hill失效系数满足约束，从而得到比传统柔度最小化(刚度最大化)更加安全的设计结果。其拓扑优化数学模型可表示为

(11)

当优化问题涉及除体积约束以外的其他约束时，一般通过构造一个包含原目标函数与其他约束的新目标函数，将有约束问题转化为无约束问题。本文构建的新优化目标函数如下：

(12)

式中，α为权重因子，α的大小控制着柔度C和失效系数约束在目标函数η中所占的比例。

2.2 材料插值方案

在传统BESO框架中，设计域被离散成N个设计变量，设计变量的存在与否由1和xmin表示，且不存在中间状态。为了避免低密度单元可能引起的应力奇异问题，采用以下插值策略：

De=xeD0

(13)

式中，D0为材料弹性矩阵；De为单元弹性矩阵。

因此，由式(13)可知，只需考虑实体单元的应力状态计算，删除的空单元应力直接置零，表达式为

(14)

式中，Be为单元应变矩阵；ue为单元位移向量。

2.3 全局失效系数度量

(15)

需要注意的是，P值趋近无限大时会使优化发生强烈震荡，因此P值需要适当选取[13]。替换后目标函数式(12)可改进为

(16)

3 灵敏度计算方法

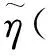
(17)

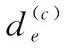
3.1 柔度灵敏度

(18)

式中，Re为变换矩阵，满足关系式ue=ReU；ke为单元位移向量；k0为实体单元刚度矩阵。

3.2 失效系数约束灵敏度

(19)

(20)

(21)

式(19)中的偏导∂σe/∂xe项满足式(14)插值模型，因此可以按照链式法则展开推导，得

(22)

将式(20)～式(22)代入式(19)中得

(23)

(24)

(25)

式中，R为伴随载荷。

4 优化求解策略

4.1 权重因子的更新

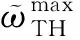
(26)

式中，q为区间控制参数，取值范围推荐为[0.9，1]。

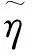
(27)

4.2 数值处理方法

与式(13)插值策略类似，对其单元灵敏度进行以下处理：

(28)

当xe=xmin时，低密度单元的灵敏度将趋于0，有效杜绝了应力奇异问题。另外有研究表明，BESO方法在处理非线性问题时，结构的进化方向容易受到前步中值较大的“主导灵敏度”影响而产生震荡[29]，因此需对灵敏度进行归一化处理，即

(29)

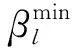
为了保证相邻单元间灵敏度的连续性以避免棋盘格现象，并确保被删除单元有机会被再次增添，需对单元灵敏度进行过滤，实现敏度再分配：

(30)

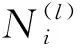
为了优化的稳定性，当前灵敏度的最终值也需考虑历史平均技术：

(31)

(32)

最后对设计变量进行密度过滤。在应力等非线性优化中，密度过滤可以获得更好的结构[13]：

(33)

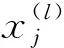
4.3 优化算法流程

所提各向异性强度约束的拓扑优化算法求解流程可归纳为如下步骤：

(1)定义有限元网格，初始化设计域和边界条件。

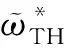
(3)通过V(l)=max(V(l-1)(1-γ)，χ)更新当前迭代步体积分数，使结构体积逐渐达到目标体积分数χ并保持稳定。

a.依据式(28)计算单元初始灵敏度；

b.依据式(29)～式(31)计算修正后的单元灵敏度值；

c.根据式(32)与式(33)更新设计变量；

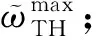
(6)重复执行步骤(3)～(5)，直至满足下式的收敛条件：

(34)

或达到目标体积后迭代一定步数并经验性停止，输出最优解。

5 数值算例

本节采用两个经典数值算例来验证所提方法的有效性。数值算例中材料的弹性模量为210 MPa，泊松比为0.3；材料1方向的屈服强度为X1，材料2方向的屈服强度为X2=ψX1，其中ψ为两正交方向的强度比。灵敏度过滤半径rs=2，密度过滤半径rd=3.5，目标体积分数为0.5，体积进化率为0.02，最大体积增添率[16-17]为0.005，P范数随优化过程从6逐渐增加到7。

为保证探究各向异性强度比ψ改变对结果影响时的公平性，定义以失效空间体积不变为调整不同强度比ψ下材料方向强度X1、X2的依据。图3a所示为X1=X2=100 MPa即ψ=1时所对应失效空间，图3b所示为X1≠X2即ψ≠1时的失效空间，已知ψ值，可通过联立空间体积相等方程计算确定相应的X1、X2值。

(a)ψ=1 (b)ψ=0.65图3 不同ψ值下的Tsai-Hill失效空间Fig.3 Tsai-Hill failure space for different values of ψ

5.1 算例1

本算例选取经典算例L形梁进行算法的验证研究，其边界条件设置如图4所示，结构划分为10 000个四节点平面应力单元，上端施加固定约束。为避免施力点的应力集中，载荷F=30 N均布在右侧5个节点上，自然坐标系标注在左下角。图5中绿色坐标系为材料坐标系，坐标轴的方向和长度分别代表材料1、2两主方向与对应方向上材料的强度极限X1、X2，右上角绘制相应优化结果的主应力失效面与约束状态，云图中红色代表高失效系数，蓝色代表低失效系数。

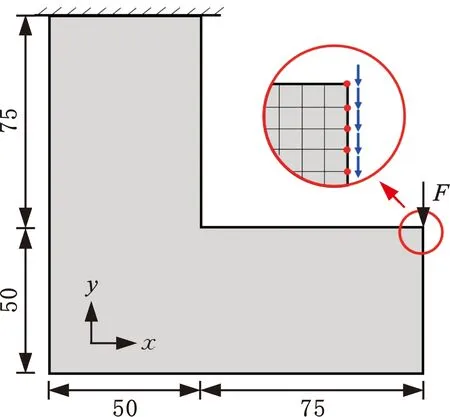
图4 L形梁问题的边界条件Fig.4 Boundary conditions for the L-beam problem

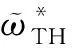
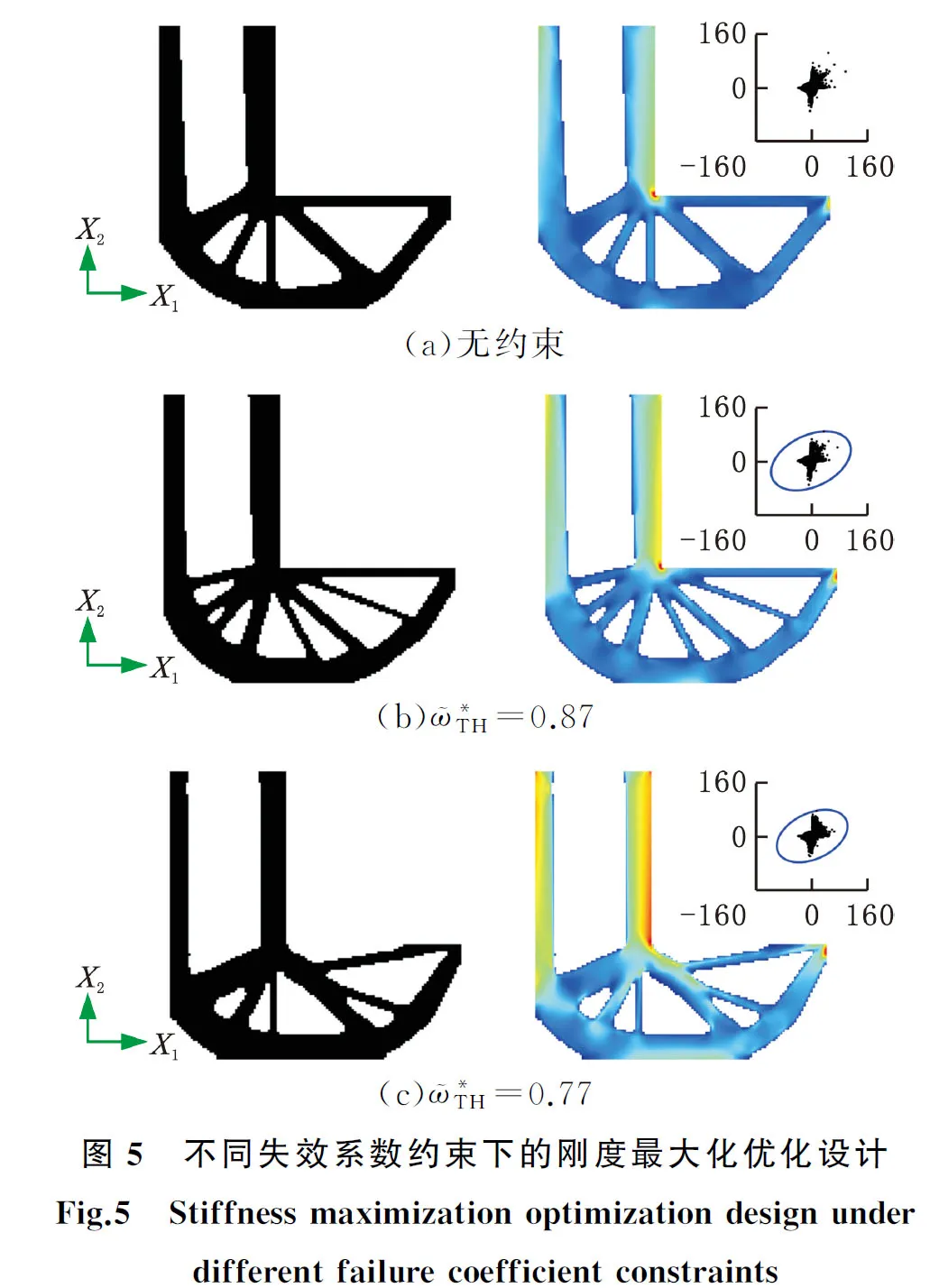
表1 不同失效系数约束下的设计性能对比

图时的优化迭代历程Fig.6 Optimization iteration process of

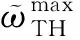
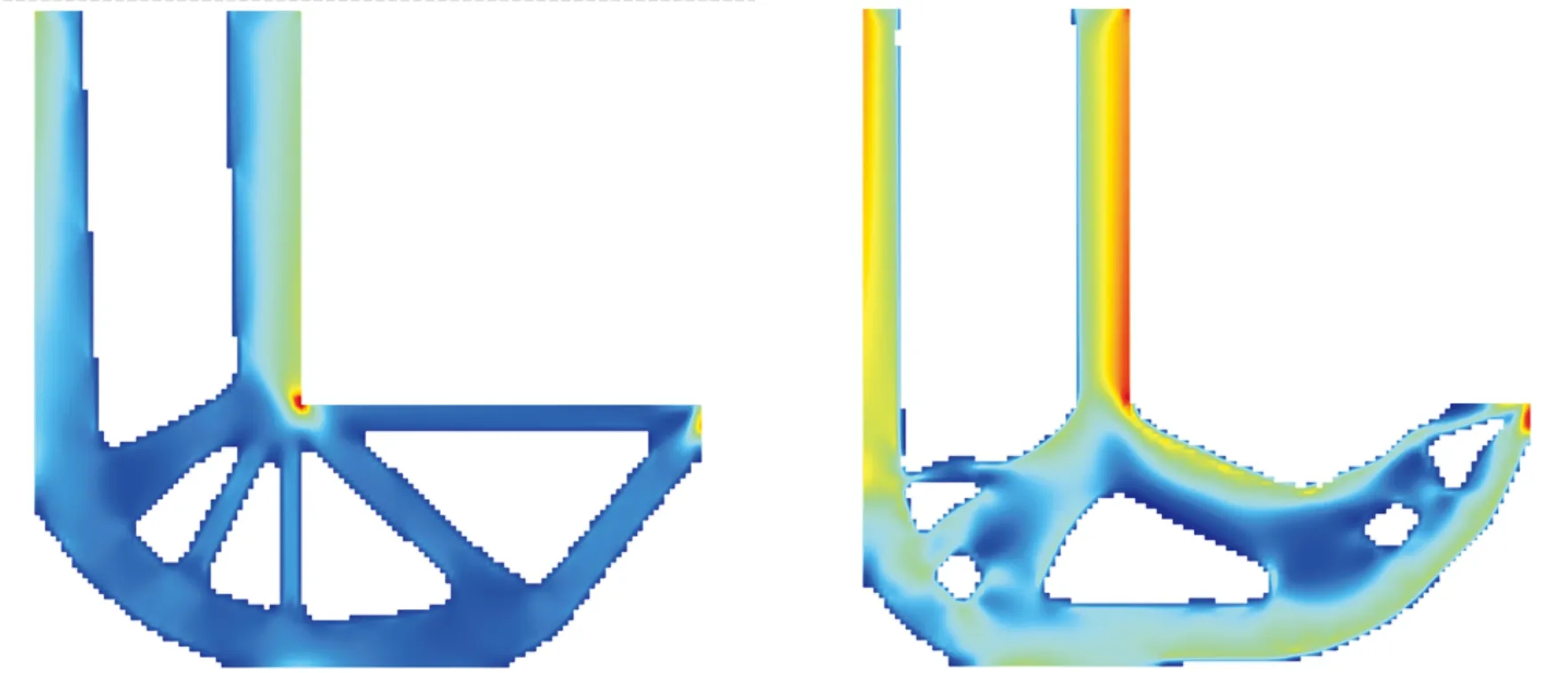
(a)无约束刚度设计 (b)von-Mesis应力设计

表2 不同优化方法设计结果性能对比

为了研究不同强度比ψ对优化结果的影响，表3左三列分别展示了ψ为0.65、1、1.5的优化结果。表3所示的失效系数分布云图中主应力的单位均为MPa。当ψ=1即材料展现各向同性强度特性时，其失效面椭圆(云图右上角)的长轴与主应力平面45°夹角方向重合，面内可包络更多刚度最大化设计的主应力点(图5a右上角)，因此较易满足约束且优化结构刚度最好。随着各向异性程度即ψ值的减小(ψ=0.65)或增大(ψ=1.5)，失效面椭圆长轴会向主应力平面横轴或纵轴靠拢，导致包络区域偏离刚度最大化设计的主应力点，约束较难满足且结构刚度均有所下降，较大的失效系数逐渐向着设计结果的纵向或横向分布。

(a)von-Mesis应力约束刚度设计 (b)Tsai-Hill失效系数约束刚度设计图8 von-Mesis应力约束与Tsai-Hill失效系数约束的主应力失效面对比Fig.8 Comparison of von-Mesis stress constraint and Tsai-Hill failure coefficient constraint failure surface

为验证增材制造材料堆叠角度变化对优化结果的影响，表3右三列分别展示了材料坐标系偏转角θ为0°、45°、90°时的优化结果。可以看出，堆叠角的改变会使结构发生明显变化，在满足相同失效系数约束的条件下，不同堆叠角下的结构刚度也会发生改变。由此可见，考虑材料堆叠角的影响对寻找增材制造结构在特定工艺下的最优解非常重要。

5.2 算例2

本算例采用T形梁进行优化验证，其边界条件设置如图9所示，结构划分为13 750个四节点平面应力单元。左右两端施加固定约束，载荷F=30 N均布在顶部中间的7个节点上，以避免施力处的应力集中，自然坐标系为图9中黑色坐标系。图10中绿色为材料坐标系。

图9 T形梁问题的边界条件Fig.9 Boundary conditions for the T-beam problem

表4 不同失效系数约束下的设计性能对比

(a)无约束

表5中右三列展示了不同材料堆叠角对T形梁优化结果的影响。可以看出，不同角度下的优化设计刚度相差较大，且相较于θ=0°与θ=90°时的对称优化结果，θ=45°时出现了明显的非对称结构，这是由于材料低强度方向随着堆叠角θ的改变而发生偏转，为满足设计性能需求，优化结果将生长出更多斜向枝干以弥补结构性能的不足。

6 结论

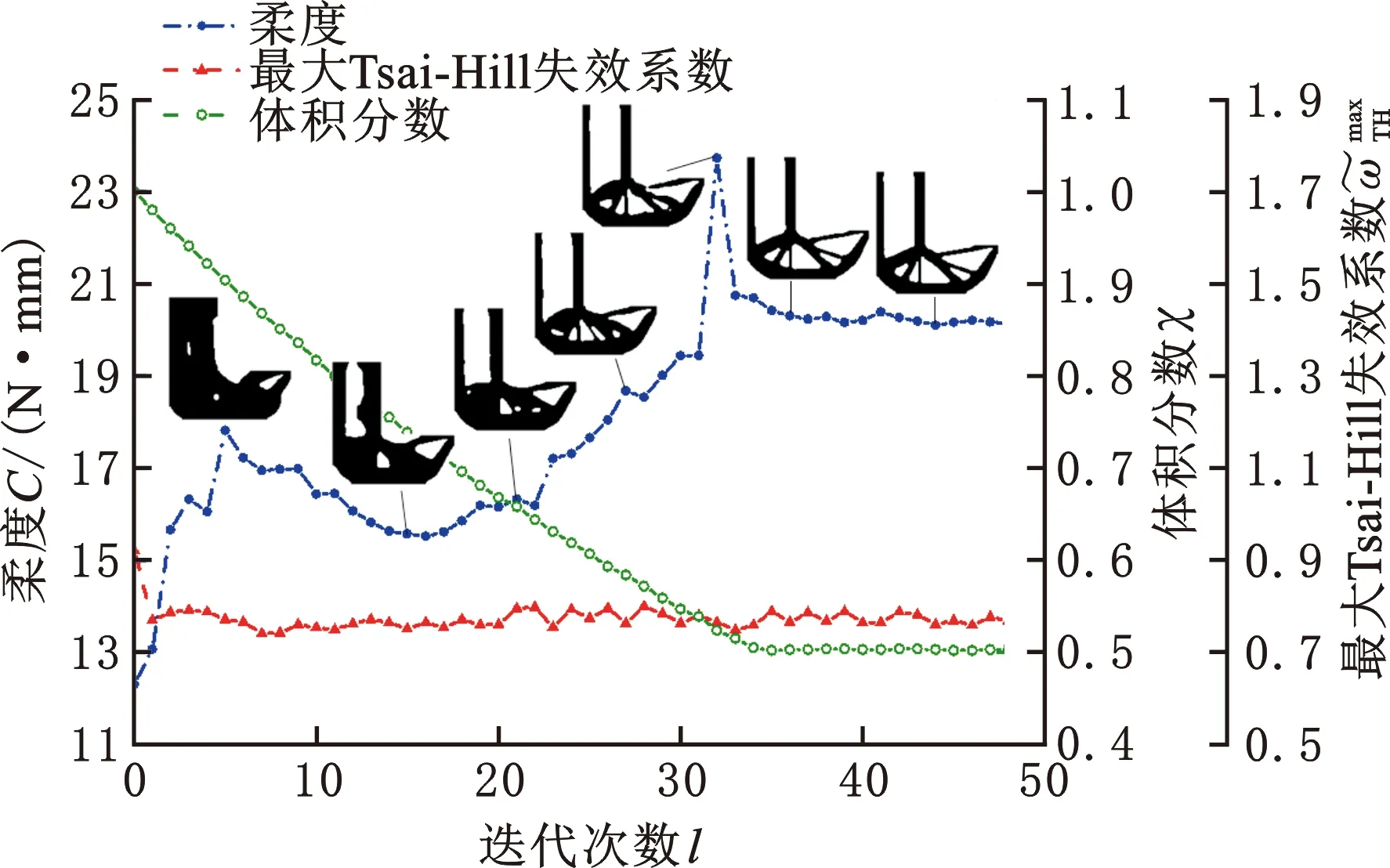
(1)本文面向增材制造工艺所引起的结构各向异性强度特性，基于BESO方法提出了一种考虑各向异性强度约束的拓扑优化策略。结果表明，传统刚度优化设计难以避免高失效风险区域，本文方法可以在优化结构刚度的同时有效抑制失效集中以保证结构强度，且优化结果边界清晰、优化过程迭代平稳。通过比较发现，在增材制造的各向异性强度假设下，本文方法可以获得比传统von-Mesis应力相关设计性能更好的结构。

(2)材料的各向异性程度与堆叠角度参数均会对优化产生很大影响。随着各向异性程度的加剧，优化结构的性能也会随之恶化，材料会趋于向强度较低的方向分布。与此同时，改变堆叠角度也会影响结构性能，即优化结果很大程度依赖于参数的调整。因此，考虑各向异性的影响有其实际必要性。