基于最大重加权峭度盲解卷积的风电故障诊断

2022-10-18王家序刘治汶

中国机械工程 2022年19期

吴磊王家序张新刘治汶

1.西南交通大学机械工程学院，成都，6100312.电子科技大学自动化工程学院，成都，611731

0 引言

风电机组长期在阵风等复杂交变载荷作用下工作，恶劣工况以及复杂机械结构严重影响机组运行安全与维护保障[1-2]。风电机组关键部件——齿轮和轴承容易出现各种形式的故障，一旦出现故障可能造成巨大损失，因此研究风电机组的运行状态监测与故障诊断具有重要意义[3-6]。

得益于振动信号中含有丰富的机械运行状态信息，振动监测成为旋转机械状态监测与故障诊断的有效技术[7-9]。然而，测量信号中由齿轮或轴承局部缺陷所引起的故障冲击序列经常被环境噪声以及其他干扰成分所掩盖，加上传递路径的传播效应，导致齿轮和轴承的故障诊断存在较大困难[10-12]。盲解卷积方法通过设计一个有限长脉冲响应(finite impulse response，FIR)滤波器，能实现在未知振动源、传输通道特性以及噪声强度的情况下从测量信号中恢复故障冲击特征，在旋转机械故障诊断领域引起了广泛的关注[13]。在设计FIR滤波器时，通常是基于信号的某种数字特征，且待恢复的信号成分与干扰成分在此特征上表现出可区分性[14-15]。如经典的MED(minimum entropy deconvolution)方法利用地震波与环境噪声在峭度方面的不同，成功获取地震相关信息[16]。MED具有调参少、收敛快等优势，但用于旋转机械振动信号分析时却倾向于恢复单个主导冲击而非故障冲击序列，原因在于相同信号长度下单个冲击的峭度远大于冲击序列的峭度。在机械故障诊断领域，MED仍得到了部分应用。ENDO等[17]结合MED与自回归(auto-regressive，AR)，提出AR-MED滤波方法并用于齿轮剥落和齿角裂纹检测；YANG等[18]利用MED对原始信号进行预处理，提取被强噪声干扰的轴承特征信息；LIU等[19]利用MED凸显故障冲击特征，使得包络分析更准确有效。然而，值得注意的是，在上述应用中，MED倾向于恢复单个冲击的缺陷并未得到有效解决。

为克服MED这一缺陷，多种盲解卷积方法被提出并应用到机械故障诊断中，其中最常见的方法包括MCKD(maximum correlated kurtosis deconvolution)[20]、MOMEDA(multipoint optimal minimum entropy deconvolution adjusted)[21]以及CYCBD(maximum second-order cyclostationarity blind deconvolution)[22]。在恢复故障冲击序列方面，这三种方法表现出优异的性能，但它们却依赖于待恢复冲击序列频率这一先验知识，即方法并非全“盲”。实际应用中，受速度波动等因素的影响，难以预先获知准确的故障特征频率，严重影响了三种方法的有效性，从而也限制了方法的适用性[23-25]。近年来，涌现出不少解卷积方法并被用于机械故障诊断中。DUAN等[26]提出利用形态滤波来提高MED的滤波效果；MA等[27]基于稀疏子空间重编码提出了一种有效的齿轮箱故障诊断方法；ZHANG等[28]利用连续振动分离这一方法克服调制效应并结合MED提出了一种齿轮故障诊断方法；MIAO等[29]采用基尼系数作为盲解卷积指标，在旋转机械故障诊断中表现出较好性能；LIANG等[30]提出的最大平均峭度解卷积方法对典型干扰具有较好的鲁棒性，但不足之处在于所提方法的有效性仍依赖先验故障特征频率。

为有效恢复故障冲击序列、准确诊断齿轮故障，本文提出了一种新的盲解卷积方法——最大重加权峭度盲解卷积方法。该方法利用重加权峭度对故障信号中单个或少量强冲击干扰具有较好鲁棒性，以及不依赖待恢复故障冲击序列先验知识的特性，能有效地解决基于峭度最大化方法倾向于恢复单个主导冲击的问题。同时，相较于常见依赖故障特征频率先验知识的非全“盲”方法，所提方法在齿轮故障诊断方面具有更强的适用性。通过仿真信号分析以及风电机组故障诊断应用研究来验证所提方法的有效性。

1 常见解卷积指标及其主要缺陷

1.1 问题描述

在旋转机械故障诊断中，受多振动源以及复杂传递路径和噪声干扰等多因素的影响，振动信号中由齿轮局部缺陷所引起的故障冲击成分往往被其他干扰所掩盖。由传感器测量得到的振动信号x一般可表示为

x=s0*gs+n*gn

(1)

式中，s0为局部缺陷产生的故障冲击成分；n为干扰成分(如高斯噪声、电流产生的强冲击干扰等)；*表示卷积运算；gs、gn分别为故障冲击成分与干扰成分的脉冲响应函数。

盲解卷积旨在设计一FIR滤波器h，从振动信号中恢复得到故障冲击成分s0，其过程如图1所示，可表述为

s=x*h=(s0*gs+n*gn)*h≈s0

(2)

其中，滤波信号s为s0的估计值。在此过程中，利用衡量指标(如峭度、相关峭度、D-范数等)来评估滤波信号以及作为目标函数求解滤波器是必要的，而不同的指标表现出不同的性能，甚至直接决定方法的有效性。

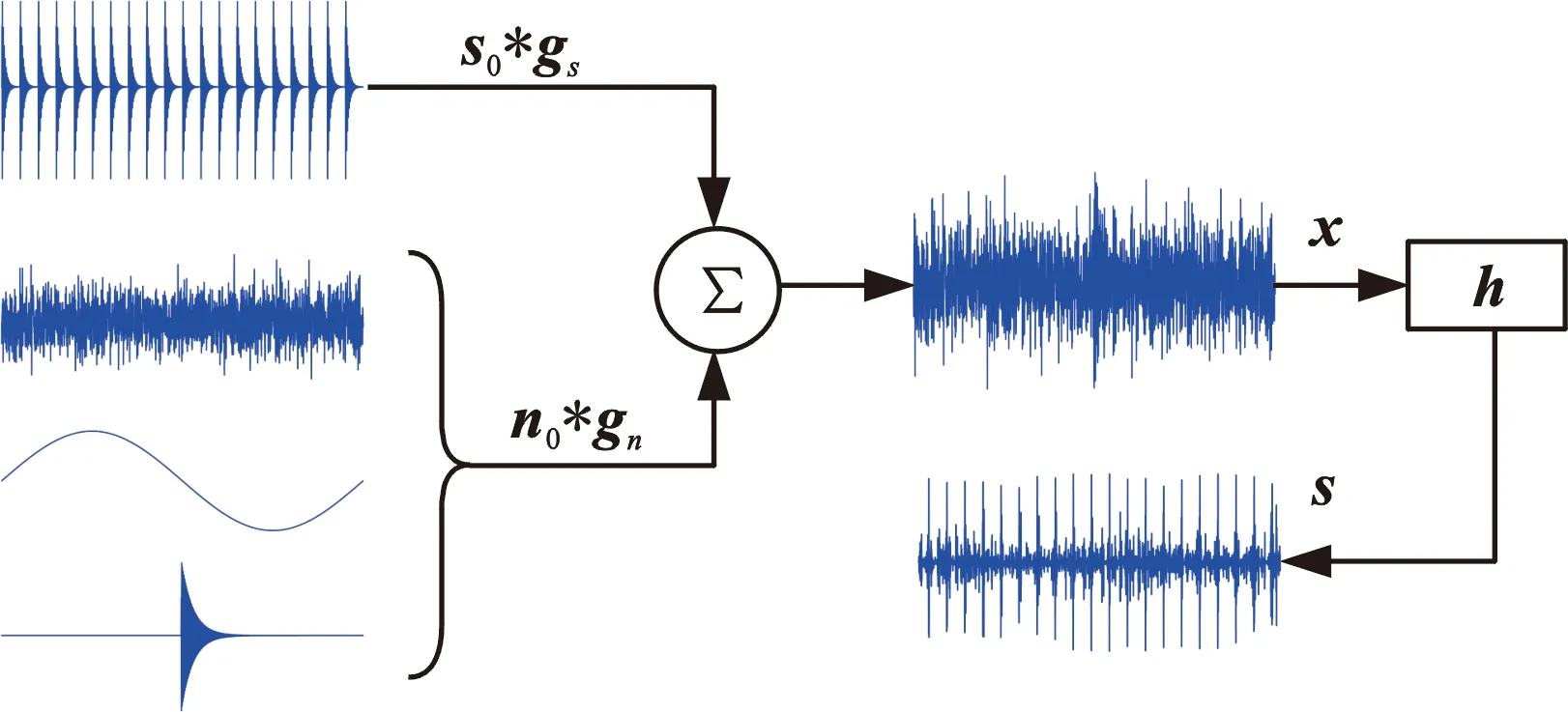
图1 盲解卷积技术基本原理Fig.1 The basic principle of blind deconvolution techniques

1.2 峭度

在MED方法中，峭度被用作盲解卷积指标。尽管此方法名为“最小熵解卷积”，但它并非使滤波信号的熵最小，而是通过最大化滤波信号的峭度来求解滤波器h，即

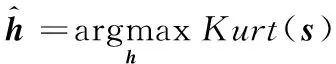
(3)

(4)

式中，Kurt(s)为零均值滤波信号s的峭度；N为信号长度；s[i]为s的第i个分量。

BUZZONI等[22]证明了在一定条件下，峭度与微分熵成相反关系。齿轮、轴承在正常运行状态下，其振动信号近似于高斯白噪声，信号峭度接近3，而当振动信号中包含由局部缺陷产生的非高斯成分时，信号的峭度会超过3，可见峭度能在一定程度上反映设备的健康状态。但正如引言中所述，使用峭度作为解卷积指标的缺陷在于，方法倾向于恢复得到单个主导冲击而非由局部故障引起的冲击序列，尤其是当测量信号中含有因电流等导致的强冲击干扰时，这一缺陷会更加明显。

1.3 其他常见解卷积指标

为解决上述问题，多种解卷积指标被提出并形成新的方法，最常见的包括相关峭度[20]、多点D-范数[21]以及二阶循环平稳指标[22]等。

基于故障冲击的周期性，相关峭度定义为

(5)

其中，Ms为位移数，Ts为故障信号周期，当Ms=1且Ts=0时，相关峭度退化为峭度。MCKD通过最大化滤波信号的CK来求解滤波器，即

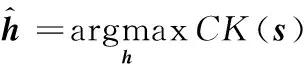
(6)

相比峭度，CK能够更好地表征冲击序列，因此MCKD在故障诊断中被广泛提及。

通过引入目标向量t，设定目标冲击的位置以及权重，MOMEDA定义了多点D-范数：

(7)

该指标充分考虑了故障冲击特征的周期性，此外，作为非迭代的求解方法，MOMEDA效率更高。

考虑到旋转机械局部故障产生的冲击序列会表现出循环平稳特性，CYCBD采用二阶循环平稳指标，定义如下：

(8)

(9)

(10)

其中，k为样本指数，L为滤波器长度。CYCBD在恢复故障冲击序列方面表现出非常优异的性能。

由上述指标计算公式可见，这三种常见方法都极大程度上依赖于先验故障特征频率，而实际应用中难以预先获知准确的故障特征频率，致使方法的适用性受到极大限制。因此，探究不依赖先验知识的全“盲”方法意义重大。

2 最大重加权峭度盲解卷积方法

为有效恢复故障冲击序列、准确诊断齿轮故障，本节介绍一种全“盲”方法——最大重加权峭度盲解卷积。信号的重加权峭度计算过程如下：

(1)对滤波信号s进行M等分，得到各子段信号sm(m=1，2，…，M)。

(2)计算各子段信号的峭度Kurtm。

(3)对Kurtm进行升序排列，并将其表示为一行向量的形式，即Kurtasc。

(4)计算Kurtm对其和的权重，即

(11)

(5)对Wm进行降序排列，同样将其表示为一行向量的形式，即Wdesc。

(6)利用重排后的权重向量Wdesc对重排后的峭度向量Kurtasc进行加权，得到信号的重加权峭度RK：

(12)

根据上述计算过程可见，当M=1时，RK退化为峭度。为直观呈现RK在表征故障冲击序列方面的优势，计算了图2所示的单个冲击与周期性冲击序列(信号长度相同)的RK值。如表1所示，单个冲击的峭度远大于冲击序列的峭度，而单个冲击的RK远小于冲击序列的RK(M>1)，同时冲击序列的峭度几乎等于其RK。因此，以重加权峭度作为盲解卷积指标，可有效地解决基于峭度最大化方法倾向于恢复单个主导冲击的问题。

(a)单个冲击

表1 不同M值下单个冲击与周期性冲击序列的RK值

M的取值不依赖具体的公式，理论上不超过信号长度的任意正整数都能使算法正常运行，但每一个子段信号长度不能太小，否则子段信号的峭度Kurtm将失去物理意义。对多组仿真信号和实际齿轮振动信号分析后发现，当M=4时，大部分数据分析均能取得理想结果，因此在使用所提方法时推荐M取值为4。

基于上述分析，最大重加权峭度盲解卷积求解FIR滤波器可表示为如下所示的最大化问题：

(13)

为求得RK最大值，令RK对滤波器系数的偏导数等于0，即

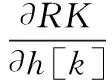
(14)

首先，

(15)

其中，Kurtθ为第θ段滤波信号的峭度，可见，式(14)是高度非线性的，难以直接求解。因此，采用迭代求解法，通过不断更新滤波器系数的方式求得方程的有效近似解。为简化运算，令∂Kurtθ/∂h[k]=0得到M个滤波器，然后对这M个滤波器加权求和即可得到更新后的滤波器，过程如下：

(16)

根据式(2)，有

(17)

(18)

则可得到下式：

(19)

进而，得到其中一个滤波器，则

(20)

(21)

其中，xθ、sθ分别对应第θ段子段信号及其滤波信号，Xθ为xθ对应的Toeplitz矩阵。从而，得到滤波器更新公式：

(22)

综上，所提方法整体流程如下：

(1)输入测量信号x，指定参数M=4，随机初始化滤波器h系数，如h=[0 0 … 1 … 0 0]T。

(2)根据式(2)计算滤波信号s，根据式(12)计算RK(s)。

(3)根据式(22)更新滤波器h系数。

(4)重复步骤(2)和步骤(3)使RK(s)达到最大。

(5)步骤(4)中最大RK(s)对应的滤波信号即为目标滤波信号。

3 仿真信号分析

本节进行仿真信号分析以验证所提方法对恢复故障冲击序列的有效性，同时将本领域常见方法(MED、MCKD、MOMEDA以及CYCBD)作为对比研究来探讨所提方法的优势。

考虑到实际测量信号中包含的环境噪声，以及可能含有强冲击干扰(如电流干扰)和谐波分量成分，仿真信号x(t)的组成如下：

(23)

式中，s0(t)为故障冲击序列(频率为取100 Hz)；b(t)为强冲击干扰；c(t)为谐波分量；w(t)为信噪比-10 dB的高斯白噪声；ρ为阻尼系数。

(a)故障冲击s0(t)

各方法的滤波信号如图4所示，可见，本文方法与MCKD、MOMEDA以及CYCBD均准确恢复了故障冲击序列，而MED只得到单个主导冲击。然而，正如1.2节所述，MCKD、MOMEDA和CYCBD作为非全“盲”方法，需要提前指定待恢复冲击序列的频率，而图4中的分析结果正是建立在指定频率完全等于待恢复冲击序列频率基础之上的。为进一步探究这三种方法对故障频率这一先验的依赖特性，图5给出了它们在指定频率为103 Hz时的滤波信号。可见，即便是指定频率与故障冲击序列实际频率存在较小偏差时，这三种方法均无法有效恢复故障冲击序列。

(a)本文方法

由上述分析可见，与同为全“盲”的经典MED相比，所提方法解决了MED倾向于恢复单个主导冲击的问题，在恢复故障冲击序列中表现出更好的潜力。而相较于常见非全“盲”的MCKD、MOMEDA以及CYCBD，本文方法在保证分析结果准确的基础上，不需要有关故障冲击的先验条件，在实际应用中具有更强的适用性。

(a)MCKD

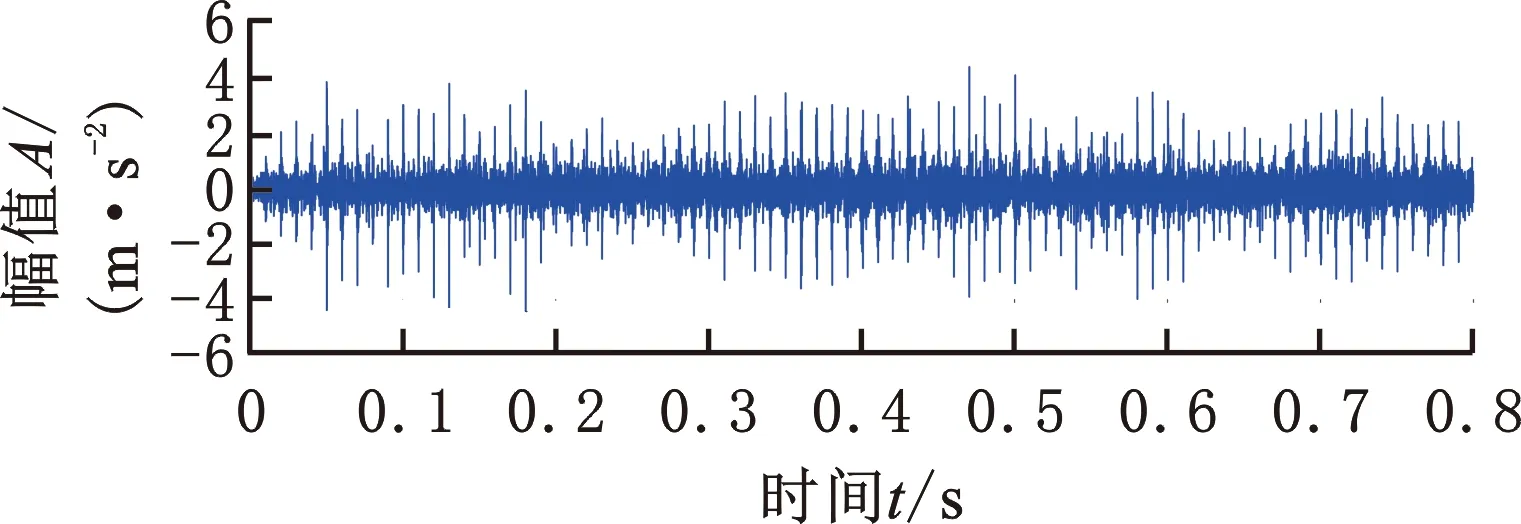
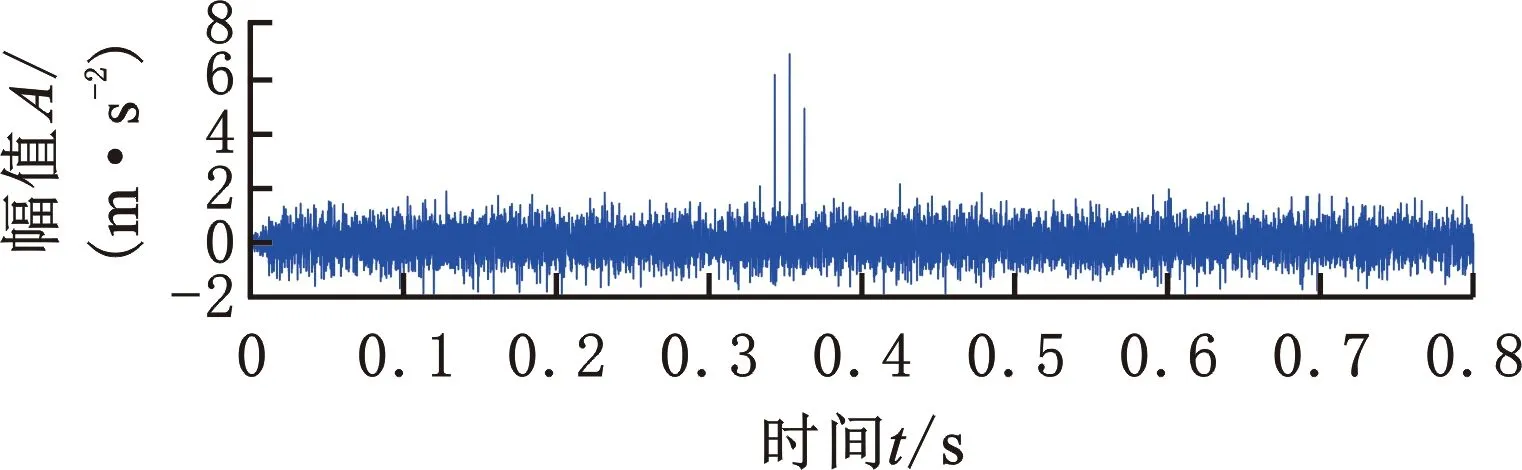
由于实际场景中测量信号还可能同时包含多个冲击干扰，因此在上述仿真信号x(t)的基础上再添加多个冲击干扰b′(t)(具体参数如表2所示)，得到新的仿真信号x′(t)。b′(t)的表达式为

(24)

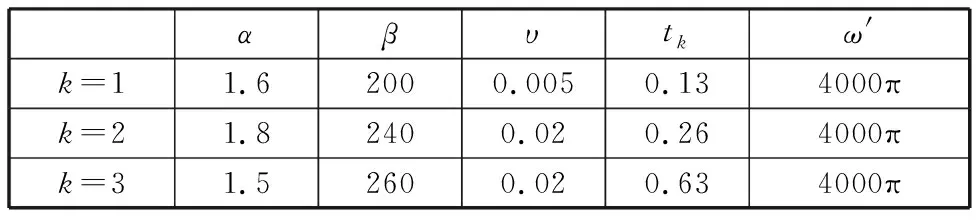
表2 b′(t)的具体参数

b′(t)和x′(t)波形分别如图6a、图6b所示，可见，仿真信号中的冲击干扰较为明显。如图6c所示，所提方法仍准确恢复了故障冲击序列，验证了本文方法对分析存在多个冲击干扰的信号的有效性。

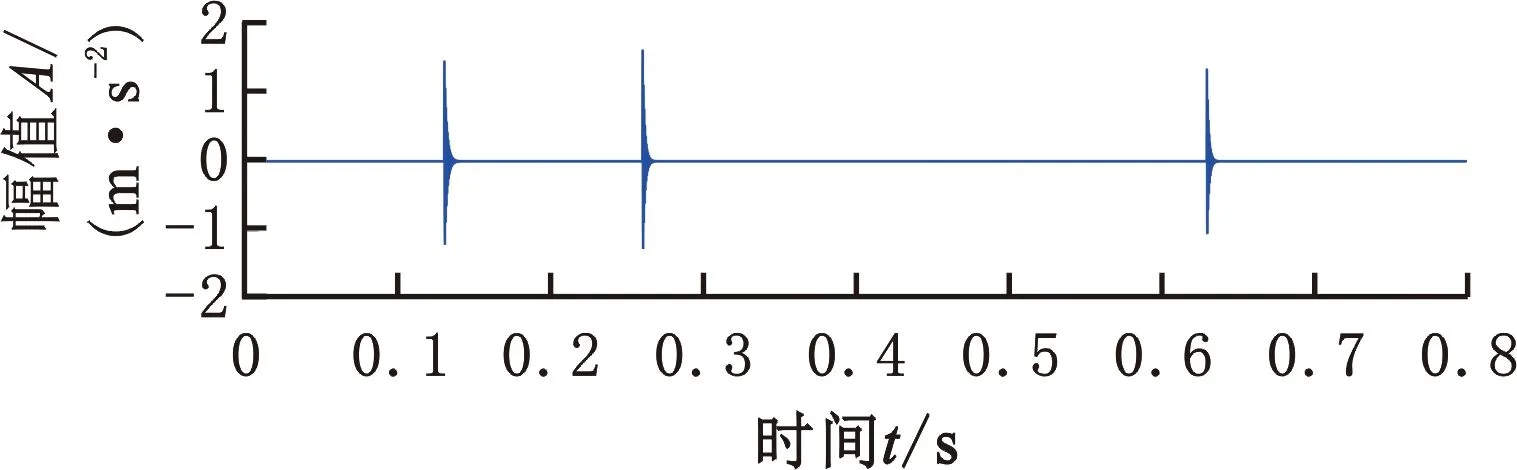
(a)多个冲击干扰b′(t)

4 风电机组故障诊断应用研究

工程应用中，由于环境噪声以及其他干扰的影响，测量信号组成十分复杂，使得故障诊断具有一定难度。本节采用风电机组故障诊断实际案例分析，来验证本文方法在实际复杂工程应用中的有效性，同时与MED进行对比研究。因上述其他方法均依赖故障频率这一先验条件，而实际信号的故障频率难以准确获知，因此本案例中不再将它们作为对比方法。

本工程数据来自于某风电机组振动监测，振动监测中，安装在齿轮箱输出小齿轮轴上方壳体表面的加速度传感器(图7)监测到了异常振动。信号采样频率为97 656 Hz，转速计测得齿轮箱输出小齿轮轴转速为1800 r/min。截取信号51 200点以分析异常振动出现的原因，如图8a所示，由于测量信号波形中观察不到任何故障特征信息，故无法对异常振动做出有效诊断。

图7 风电机组传动系统及齿轮箱输出轴小齿轮的加速度计测点位置示意图Fig.7 Schematic diagram of wind turbine transmission system and accelerator location of the output pinion gear

本文方法与MED的滤波信号分别如图8b、图8c所示，同时滤波信号对应的包络谱分别如图9a、图9b所示。根据滤波信号，本文方法恢复得到的周期性冲击序列的频率为29.6 Hz(1/0.0338 Hz)，十分接近输出小齿轮理论故障特征频率(30 Hz)。此外，在其滤波信号的包络谱中，可以清楚地观察到小齿轮故障特征频率及其多组倍频。因此，可初步认为小齿轮存在故障。在之后的停机开箱检测中发现输出小齿轮某一轮齿确已出现损伤(图10)，验证了本文方法的有效性。相比之下，MED的滤波信号却得到的是单个主导冲击，如图8c所示。并且，在其滤波信号的包络谱中只有故障频率处的谱线比较明显，无法观察到其他倍频成分，如图9b所示，因此仍难以对异常振动做出准确可靠的诊断。