核动力系统蒸汽发生器U 形管流致振动数值模拟

王莹杰，王明军,*，王树强，田文喜，秋穗正，苏光辉

（1.西安交通大学核科学与技术学院，陕西 西安 710049；2.大亚湾核电运营管理有限责任公司运行部，广东 深圳 518124）

蒸汽发生器是压水堆连接一、二回路的核心设备，其有效性关乎核反应堆的安全稳定运行，是核动力系统的重点研究设备[1]。传热管作为蒸汽发生器中的关键部件，是核动力系统的一回路压力边界和传热边界。压水堆核电站的运行经验表明，蒸汽发生器传热管断裂事故在核电厂事故中居首要地位[2]。在高温高压的环境中，二次侧流体冲刷传热管束，会引起传热管振动，即流致振动现象，这一现象可能进一步导致换热管的破裂损伤[3]，造成冷却剂泄漏，破坏蒸汽发生器的安全性和完整性。因此，对蒸汽发生器传热管的流致振动现象进行研究具有重要的意义。随着计算机技术的发展，流固耦合方法也被广泛应用于核电厂结构完整性及流致振动等现象研究中[4,5]，关于蒸汽发生器的双向流固耦合研究[6,7]基于WORKBENCH 平台，计算过程数据交换缓慢，且只分析了传热管的稳态热应力。冯志鹏[8]利用CFD 计算软件用户自定义函数,通过Newmark-β 方法计算圆管结构动力学方程求得涡激振动圆管的振动特性。传热管潜在的激励源包括存在于管子内侧的一次侧流体、机械诱发振动，以及存在于管子外侧的二次侧流体作用，分析表明：引起传热管恶化的主要振动原因来自于二次侧流体的激励作用[9]。本文将基于Newmark-β 方法，开发基于FLUENT 的先进压水堆蒸汽发生器U 形管流致振动模型，开展蒸汽发生器传热管在二次侧流体冲刷作用下流致振动现象的数值模拟。

1 数值计算方法

1.1 控制方程及求解流程

流体域控制方程为二维不可压缩粘性流体的连续性方程和Navier-Stokes 方程，在惯性坐标系下，二者表达式如下：

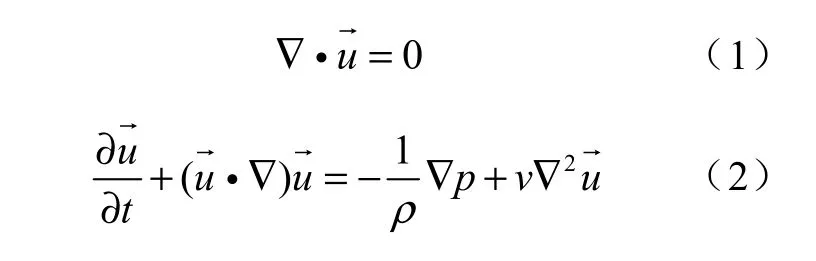
式中：ρ——流体密度；

v——运动粘度系数；

——速度矢量；

p——流场压力。

传热管在流场中的振动可简化为质量 -弹簧 -阻尼系统，其两自由度模型结构振动方程为：

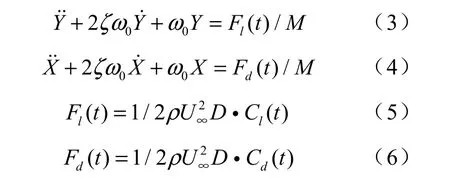
其中：U∞——均匀来流速度；

ζ、ω0——系统的阻尼比和圆频率；

M——单位长度管的质量；

Fl和Fd——单位长度管体受到的升力和阻力；

Cl和Cd——升力系数和阻力系数；

Y、、——管横向位移、速度和加速度；

X、、——管流向位移、速度和加速度。

本文基于松耦合分区方法求解传热管的流固耦合振动，流体域计算采用基于有限体积法的CFD 通用求解程序FLUENT 完成；结构域的求解通过在C 语言环境下自编Newmark-β 算法完成[10]，通过Fluent 用户自定义函数（UDF）与主程序链接求解管的振动响应；网格域根据振动响应，采用动网格模型不断更新，本文数值方法实现流程图如图1 所示[11]。

图1 流固耦合计算流程Fig.1 Fluid-structure coupling calculation process

1.2 计算模型及边界条件

本文以典型压水堆蒸汽发生器单根U 形管半圆形弯头为研究对象[12]，计算模型如图2 所示，U 形管的材料为Inconel690，其结构和物理参数如表1 所示，当流体从下至上流动时，流体掠过管外壁，则从侧方看，计算几何模型可简化为圆形截面的管外绕流，如图3 所示。矩形计算区域均为35D×20D，模型上游来流区域为10D，下游尾流区域为25D，离上下边界各为10D，D为与来流方向垂直的特征长度，即管外径。流场采用结构化网格进行离散，对管壁附近和尾流区域等参数梯度变化较大计算敏感区进行局部网格加密，网格划分示意图如图4 所示。蒸汽发生器U 形管弯头区域二次侧流体为空泡份额0.9 左右的高温高压水蒸气，计算所得流体计算域的平均物性参数如表2 所示。流体从左至右流动（相当于二次侧流体从下至上流动），左侧边界为速度入口，来流为均匀速度，右侧边界为压力出口，上下边界为自由滑移边界，振动管外形所形成的边界为运动边界，该边界为数据传递的耦合面，设定为无滑移壁面。

表1 U 形传热管几何及物理参数Table 1 Geometric and physical parameters of U-tube

续表

表2 流体物性参数Table 2 Physical parameters of fluid

图2 单根U 形管半圆形弯头模型Fig.2 Semicircular elbow model of single U-tube

图3 计算模型Fig.3 Computational model

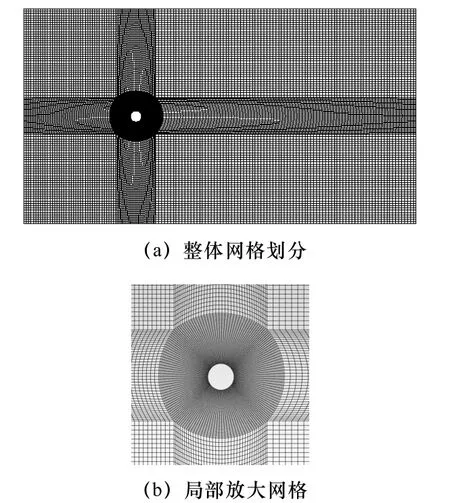
图4 网格划分结果Fig.4 Meshing results

2 数值方法验证

根据蒸汽发生器二次侧流体速度范围，求得雷诺数大小在3×104到3×105范围内，这一范围属于圆管绕流雷诺数的亚临界区，管壁上分离的剪切层开始向不规则的湍流状态转变，一部分动能由湍流所携带，出现周期性的漩涡脱落。CFD 中的DES 湍流模型可以有效的描述亚临界区圆管绕流的特性，并且较于大涡模拟和雷诺时均方法在计算效率和准确性上有一定优势[12]。本文采取DES 湍流模型开展计算，计算可得截面的升力及阻力系数，对升力及阻力系数进行快速傅里叶变换（FFT）即可得到升力、阻力系数无量纲主频，反应漩涡脱落频率的Strouhal 数St 可由式（7）求得：

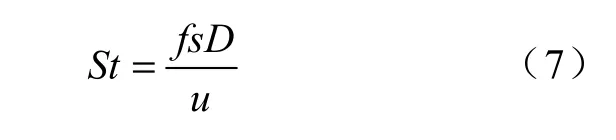
式中：fs——升力系数无量纲主频，即漩涡脱落频率；

D——特征长度，即管外径；

u——入口平均速度。

在计算前首先对网格无关性进行验证，图5所示为计算得到的阻力系数均值以及Strouhal 数随网格数量的变化情况。由图可知，当网格数量达到56 742 时（第5 套网格），阻力系数Cd和St数几乎不再随着网格数量的增加而变化。表3为56 742 网格数量下的计算结果和文献中（相同雷诺数下）的结果对比。由图5 和表2 可知，第五套网格可以认为是本模型的网格独立性解，且验证了文中数值模拟的正确性。图6 给出了阻力系数和升力系数的时间历程曲线，可以看到阻力系数和升力系数均呈现规则的周期性震荡，由于是二维模拟，没有体现出绕流的三维特性，所以和文献[13]的三维模拟的震荡效果稍有差异，但图中阻力系数和升力系数的波动趋势和文献[13]是一样的，同样没有相位差异。图8为流体域的速度云图，可以看到流体流过传热管后，在尾流区域形成周期性脱落的对称漩涡。

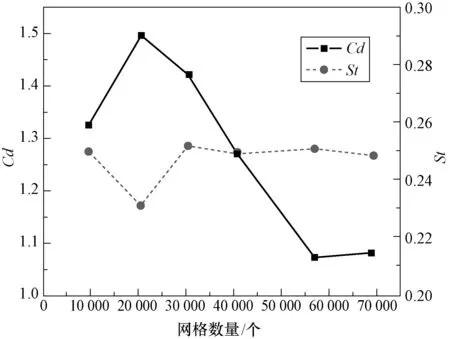
图5 网格无关性验证Fig.5 Grid independence analysis

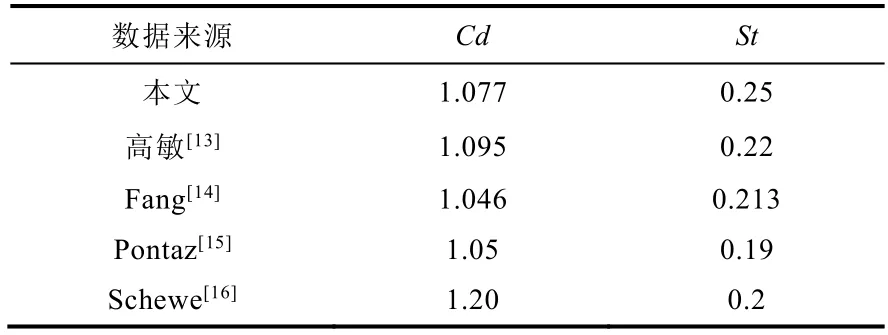
表3 计算结果和文献结果比较Table 3 Comparison of calculation results and literature results

图6 验证模型升力系数和阻力系数时程图Fig.6 Time history diagram of lift coefficient and drag coefficient for verification model

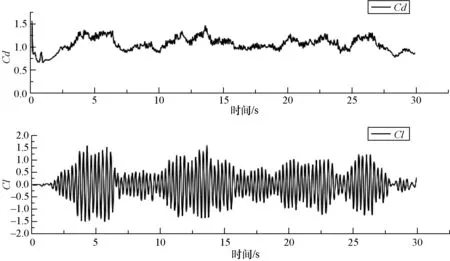
图7 文献[13]升力系数和阻力系数时程图Fig.7 Time history diagram of lift coefficient and drag coefficient for reference [13］.

图8 流体域速度云图Fig.8 Velocity contour of fluid domain

3 模态分析

模态分析是研究结构动力学动力特性的一种方法，一般应用在工程振动领域。模态是指机械结构的固有振动特性，每一个模态都有特定的固有频率、阻尼比和模态振型[17]。为求解两自由度结构振动方程，首先需要对U 形管弯管段进行模态分析，以获得系统的阻尼比和圆频率。系统的模态分析只与系统的质量、转动惯量、刚度、边界条件有关，而与外加载荷没有关系，由于系统的低阶模态对振动响应影响较大，而高阶模态可以忽略不记[18]，一般只进行较低阶次的模态分析。图9 给出了A、B、C、D 四种不同约束方式的U 形管模型，弯管两底端采用固支约束，圆弧上约束为简支约束，分别模拟具有不同数目防振条的U 形管约束。表4 给出了四种模型模态分析得到的U 形管前四阶振动频率。由表可知，随着防振条数目增加，U 形管一阶振动频率增大，当U 形管没有防振条时（A 模型），一阶振动频率和二阶振动频率差别较大；当U 形管增加防振条固定时，一阶振动频率和二阶振动频率差别较小，且均出现两两相邻阶数频率相近的现象。

图9 不同约束方式的U 形管模型Fig.9 Model of U-tube with different constraints

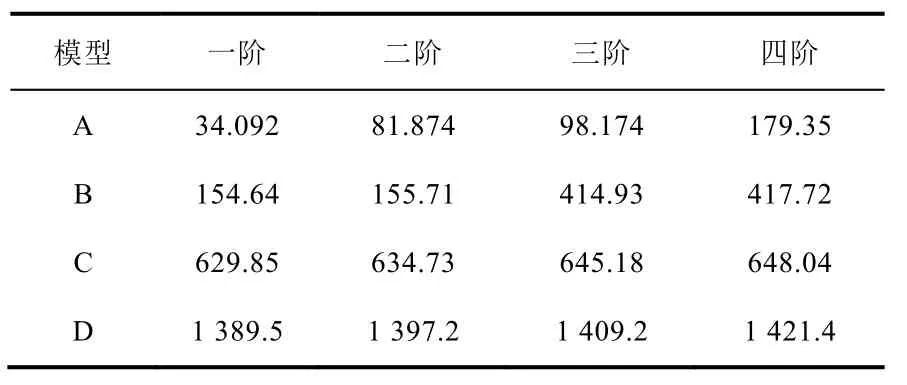
表4 模态分析结果Table 4 Results of modal analysis Hz

4 结果分析

一般情况下，模型一阶振动模态对结构影响最大，因此本文取U 形管一阶振动模态分析结果求解两自由度振动方程。根据第三部分模态分析结果以及传热管物性及结构参数确定公式（3）、式（4）中的系数，再通过Newmark-β数值方法，求解两自由度的振动方程，实现传热管涡激振动现象的模拟。图10 所示为A 模型在雷诺数等于1×105时，传热管涡激振动的升力系数时程图，图11（a）、图11（b）分别为涡激振动阻力系数、升力系数经过傅里叶变换得到的频谱图，由图可知，阻力系数和升力系数都存在振动的主频率和一个附加频率，这说明涡激振动传热管漩涡脱落频率同时受到传热管自身固有频率和激振力频率的影响，阻力系数振动变化主频率为升力系数振动变化主频率的2 倍。图12 为传热管流向、横向的无量纲位移时程曲线，由图可知，在涡激振荡作用下，传热管在流向方向上产生位移，且在一定位移范围内来回振动，而在横向方向上下振动，位移均值为零。图13 为传热管横向位移频谱图，其主要频率大小约为 20 Hz，这与涡激振动传热管的涡脱频率、固定传热管的涡脱频率接近；横向振动幅值较小，说明传热管涡激振动对流动扰动不大。图14 为不同约束条件下，传热管的横向振动无量纲位移时程曲线图，由图可知，是否安装防振条对传热管的横向位移影响较大，B 型约束传热管横向振动位移为A 型约束传热管横向振动位移的1/100，而防振条的数目对横向振动位移的影响不大，这是由于本文只研究了U 形管半弯头的最顶部圆截面，以及只考虑了一阶振动模态。图15 展示了不同雷诺数条件对A 型约束传热管涡激振动的阻力系数、升力系数、传热管横向位移、流向位移影响时程图。由图15（a）、图15（b）可知，流动的升力系数和阻力系数都呈现周期性变化现象，随着雷诺数的增加，阻力系数和升力系数的周期都逐渐变小，同时阻力系数振动的幅值越来越小，升力系数振动幅值基本不变。由图15（c）、图（d）可知，随着雷诺数的增加，传热管的流向位移逐渐增大，横向位移也逐渐增大，说明传热管的振动现象受流体湍流激振力的影响较大。

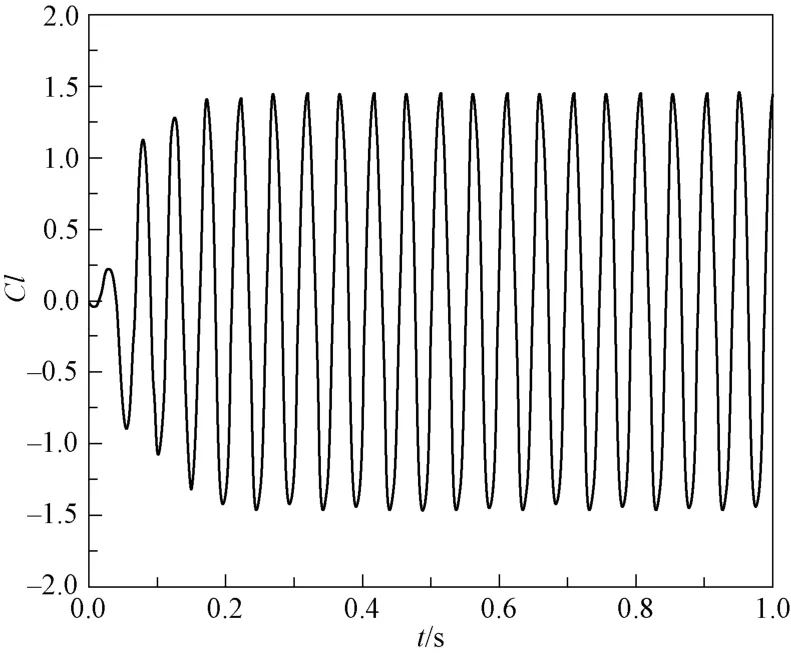
图10 A 模型传热管升力系数时程图Fig.10 T ime history diagram of lift coefficient for model A tube

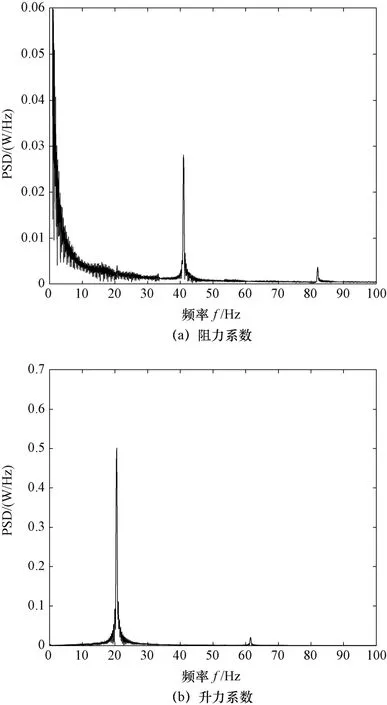
图11 频谱图Fig.11 Spectrum of lift and drag coefficients

图12 U 形管无量纲位移时程Fig.12 Time history of dimensionless displacement of U-tube

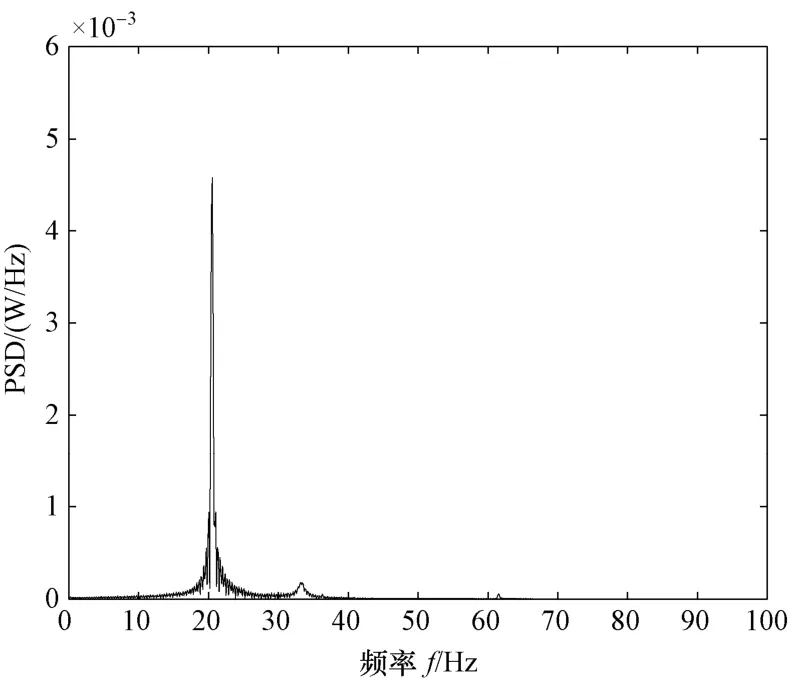
图13 U 形管横向位移频谱图Fig.13 Transverse displacement spectrum of U-tube

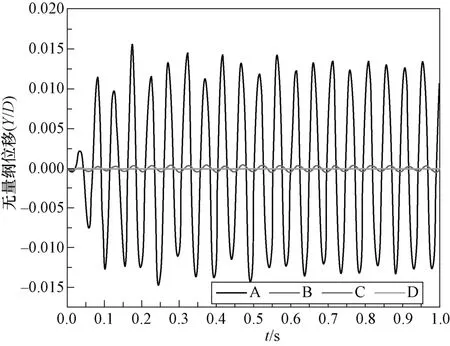
图14 不同约束条件下U 形管无量纲位移时程图Fig.14 Time-history diagram of dimensionless displacement of U-pipe under different constraints

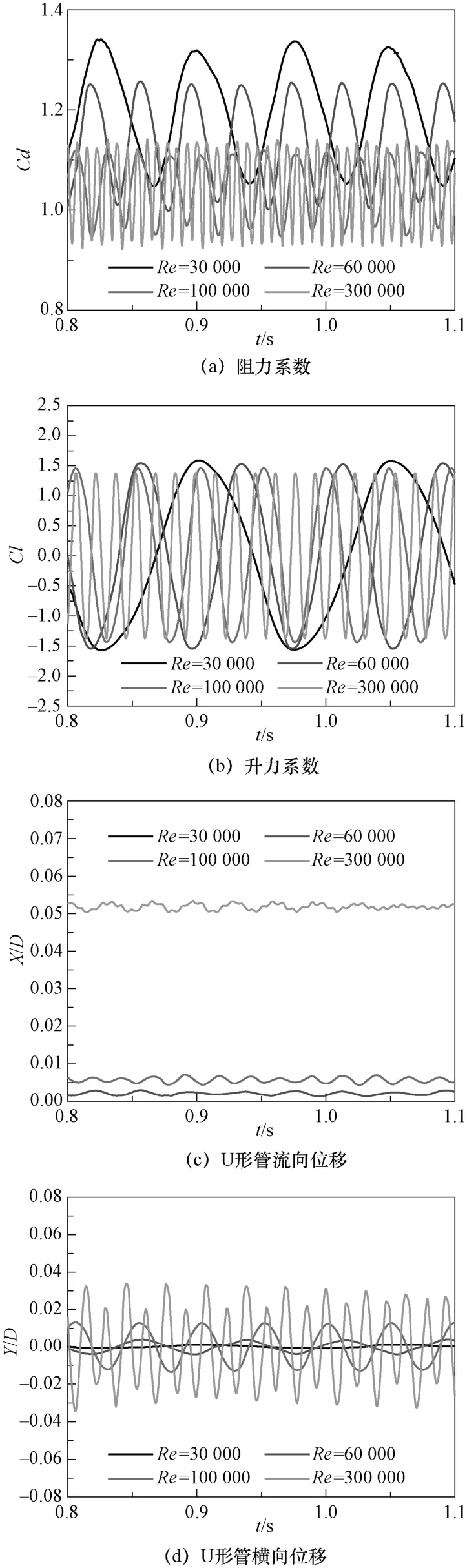
图15 不同雷诺数下涡激振动计算结果时程图Fig.15 Time history diagram of vortex-induced vibration of U-tueb at different Reynolds numbers

5 结论

本文通过在FLUENT 程序中求解结构振动Newmark-β 方程，基于动网格模型开发了适用于压水堆蒸汽发生器传热管流致振动数值模的双向流固耦合方法，开展了典型压水堆蒸汽发生器U 形传热管弯管的流致振动数值模拟。结论主要如下：

（1）随着U 形管防振条数目的增加，U 形管的固有频率增大，当U 形管没有防振条时，一阶振动频率和二阶振动频率差别较大；当U形管增加防振条固定时，一阶振动频率和二阶振动频率差别较小，且均出现两两相邻阶数频率相近的现象；传热管的流向振动会对横向振动产生影响，因此在计算过程中应该求解双自由度振动方程。

（2）在传热管涡激振动中，传热管在流向方向上产生位移，且在一定位移处来回振动，而在横向方向上围绕中心点上下振动，位移均值为零；传热管涡激振动对流体的扰动不大，单传热管漩涡脱落频率同时受到自身固有频率和激振力频率频率的影响，阻力系数傅里叶变化得到的主频率是升力系数傅里叶变换得到的主频率的2 倍。

（3）传热管在涡激振动影响下，是否安装防振条对传热管的横向位移影响较大，B 型约束传热管横向振动位移为A 型约束传热管横向振动位移的1/100；随着雷诺数的增加，阻力系数和升力系数的周期都逐渐变小，但阻力系数振动的幅值越来越小，升力系数振动幅值基本不变。随着雷诺数的增加，管的流向位移、横向振动幅值都逐渐增大，传热管的振动现象受流体湍流激振力的影响较大。