极小样本下钠冷快堆主泵上部轴承可靠性评估方法对比分析

郭晓娴，叶尚尚，谷继品，张健鑫，翟晓

（中国原子能科学研究院，北京 102413）

主泵是钠冷快堆中最关键的设备之一，主要功能是为一回路液钠的循环提供动力。主要由电机及电机支架、联轴器、电控系统、上部组合轴承、气体轴密封、检修密封、泵盖、主轴、泵体、隔热板、静压轴承、叶轮、蜗室、流量计、截止阀驱动装置等组成。为确保主泵能在规定的工况下、规定的时间内完成规定的功能，需要对主泵提出可靠性指标要求。可靠性指标验证工作所面临的最大问题是工期和经费，因此如何用最小的试验样本量得到相应的可靠性评价指标是目前面临的重要难题。故针对钠泵部件上部轴承的高可靠性要求、可试验数量少的情况展开可靠性评价方法研究的工作迫在眉睫。

1 极小样本评估方法

1.1 半经验法

半经验评估方法的思想是充分利用这些大量工程试验的经验信息，结合现场试验数据，根据数理统计和可靠性评估理论来对数据进行分析处理，得到一个在一定的误差范围内满足工程需要的评估结果。

半经验评估法的数学描述如下[1]：

设随机子样T=(T1,T2,…,Tn)来自服从对数正态分布的寿命总体T，令Y=lgT，则得到服从正态分布的总体Y～N(μY,)，同时得到对应的随机子样Y=(Y1,Y2,…,Yn)。

由数理统计理论可知

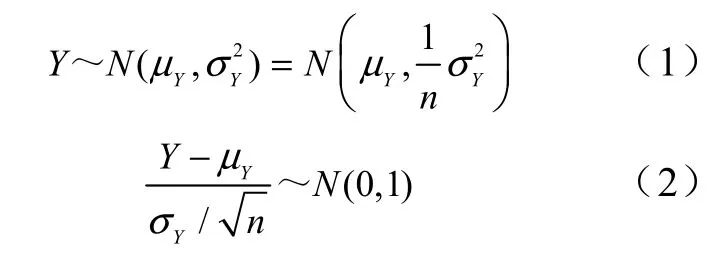
式中，σY可以由工程经验给出，一般取为0.13～0.17。而μY随着具体的结构疲劳寿命总体不同而不同。由数理统计理论可知，样本均值是总体均值的最小方差无偏估计，所以μY的值可以用样本均值的估计值代替，即。

经定置信度1-α时，Y的 100(1 -α) %置信下限表示为

从而得到试验寿命的 100(1 -α) %置信下限为

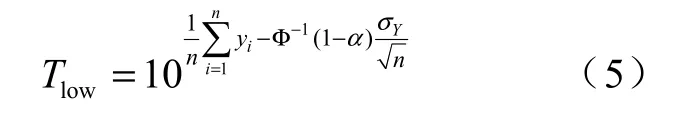
1.2 综合概率分布评估法

现有的极小子样可靠性试验评估方法的精度都相当低[2-5]。当产品为高可靠性产品时，评估方法的精度就更低。因此，如何由极小样本容量数据得到寿命的分布特性以及寻找精度更高的可靠性数据处理方法是重难点。本文综合利用历史信息和当前试验数据对样本量为1 时进行可靠性评估。大量文献及统计数据表明，与机械部件疲劳、磨损、腐蚀等耗损型失效相关的寿命分布大多可用对数正态分布或威布尔分布来表征[6,7]。根据文献［8］中的先验信息，推力滑动轴承启停阶段的累积磨损量服从对数正态分布。根据文献相关信息及计算，主泵滑动轴承的对数标准差取0.129 7[9]，滑动轴承磨损耐久寿命试验结果为582 次。

综合概率分布评估法可用于单样本试验评估，基本思想是根据一次试验结果对经验概率密度函数进行修正得到当前概率密度函数，然后与经验概率密度函数综合得出验后概率密度函数，从而对未知参数进行推断估计。综合概率方法的主要执行步骤为[10,11]：

（1）据类似件试验确定待试件的验前概分布特性；

（2）确定一个试验件时的单件值当前密度分布特性。

以单次试验值的对数为均值估计，即

在当前概率密度函数的整个定义域内，经验概率密度函数都减去fT,ex，le（或fT,ex,rl），并乘以一个大于1 的修正系数k，即可得到当前概率密度函数fT,cu

根据概率密度函数的性质，则

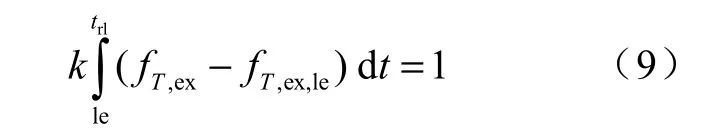
求解上式，即可确定修正系数k。

确定综合概率密度函数的步骤是提出下述加权综合法，加权系数可有正负值，在采用下述公式时≤0 .5，γ值越大代表越强调当前分布，则

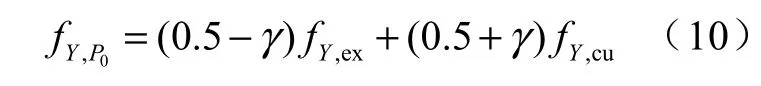
式中：下标p0代表验后概率密度分布；γ的取值在分级较粗时，建议可按下述3种情况取值，即γ1=-0 .2,γ2= 0,γ3= 0.2。

1.3 虚拟增广样本评估法+Bootstrap 方法

虚拟增广样本评估法是针对极小子样试验评估而提出的，其基本思想是把原始试验样本虚拟增广至小样本，然后应用Bootstrap 方法对小样本进行评估，Bootstrap 方法能很好地解决试验样本量n＞10 的子样可靠性评估问题。在工程允许范围之内，虚拟增广的过程需要满足以下两个基本条件[12]即：

（1）虚拟增广后的子样均值应与原来的子样均值相等；

（2）虚拟增广后的子样标准差应与类似件的标准差相等。

根据原始试验样本均值T以及以往类似件试验估计得到的分布型形式和标准差，即可虚拟增广试验样本。为使虚拟增广得到的样本更合理，建议用以下近似公式增广原始试验样本。

把增广样本T1～T13代入方程组（12）中，即可求解得到ξ的表达式为

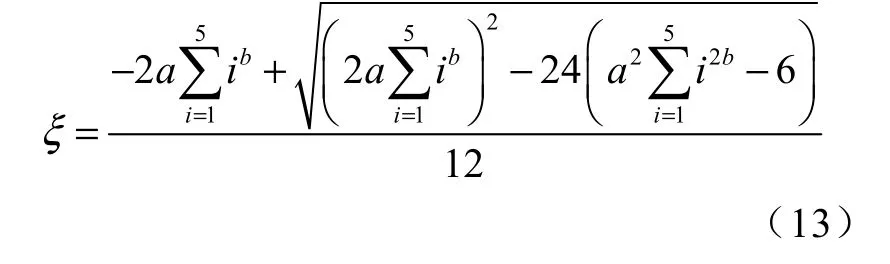
原始试验样本被增广后，即可应用Bootstrap方法对增广样本进行评估，得到未知参数的估计。

Bootstrap 方法是用现有的样本去模仿未知的分布，充分利用了样本本身的信息，对于分布不需要做出假设，运用模拟再抽样技术代替理论分析，用试验观测数据的统计特性代替真实母体的特性。Bootstrap 方法的数学描述是：设随机样本X=[x1,x2,…,xn]来自未知的总体分布F，R(X,F)为某个预先选定的随机变量，是X和F的函数。根据观测样本X=[x1,x2,…,xn]计算R(X,F)分布特征[13]，其步骤流程归纳如图1所示。

图1 Bootstrap 基本计算步骤流程Fig.1 Bootstrap basic calculation steps

应用Bootstrap 方法估计μ和σ2的具体步骤如下：

根据式（14）、（15）计算得到样本X的均值和方差S2；

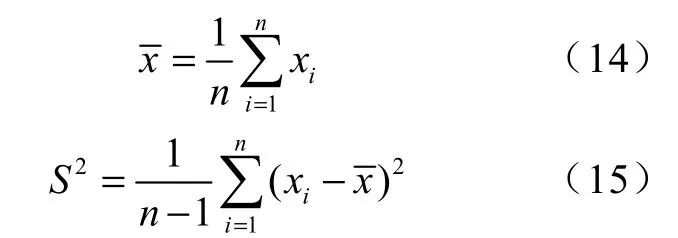
将x1,x2,…,xn按由小到大排列，利用式（16）确定样本X的经验分布Fn，并从中随机抽样产生N组自助样本（N足够大）：X*(1)，X*(2)，…，X*(N)。其中，

2 钠冷快堆主泵上轴承磨损可靠性评估

钠泵上部轴承的可靠性指标要求为：125次载荷循环（5 年）寿命可靠度P≥0.999 9，置信度γ≥0.9。滑动轴承的主要失效模式是磨损，在主泵实际工况中，磨损的发生主要在启停阶段。基于钠泵实际运行工况下的载荷剖面、转速、环境温度、冷却水温度及流量等参数，模拟相关参数环境，搭建试验台架，让轴瓦处于相应的状态进行启停磨损寿命试验，启停582次后进行性能试验验证，发现相关参数无异常。将582 次启停磨损试验保守的作为一次完全数据分别采用三种计算方法进行可靠性评估，详细情况如下。

2.1 半经验法

试验得出滑动轴承的寿命（循环次数）N0=582 次，根据经验知寿命N服从对数正态分布的随机变量，令T=lgN，则T是一个服从正态分布的随机变量，来自于正态总体T的样本对数均值也是一个随机变量。根据文献相关信息及计算，总体T的对数标准差σT= 0.129 7，基于半经验评估法的步骤如下。

（1）把正态分布变量T转换为标准正态分布Z。

（2）90%置信度的下限值计算

由γ=0.9，根 据 Φ (Zlow) =γ，得Tlow=2.5516，寿命试验对数均值的下限：

（3）任务可靠度计算

任务寿命的可靠度计算式为

式中：P′ ——任务寿命的可靠度评估值；

T′ ——任务寿命的对数值，即T′=lg125= 2.096 9。

代入寿命下限和对数标准差后可计算得到P′=0.999 772。

2.2 综合概率分布评估法

轴承轴瓦试验寿命为582 次，则样本的对数均值= lgN0= lg 582= 2.764 9，对数标准差σT=0 .129 7，对应的经验概率密度函数的形式为

可求得系数k=2.092 8，当前概率密度函数为

定义域为［2.570 4，2.959 5］。

根据单次试验值扩展而得到当前概率密度函数后，为了进一步综合考虑验前经验概率密度函数，概率密度函数需考虑加权系数。

取加权系数ω=0[10]，即得到综合概率密度函数。

经验概率密度函数、当前概率密度函数以及综合概率密度函数的对比见图2。

图2 不同概率密度函数对比图Fig.2 Comparison of different probability density functions

在置信度γ=0.9 下，可由式（28）得到试验寿命对数均值置信下限，Tlow=2.593 5，Nlow=392.259 1。从定性角度出发，在任务125次时，处于曲线图的最左侧，这时，综合概率密度函数为经验概率密度函数的0.5 倍，故可知，其任务可靠度高于经验概率密度函数对应的任务可靠度。经验概率密度函数的任务可靠度为求出结果为0.999 869。

2.3 虚拟增广样本+Bootstrap 方法

根据虚拟增广方法的原理将原始试验样本量从n=1 虚拟增扩至n*=13，取定控制系数a和b后，应用式（11），得到增广样本T1～T13，然后采用Bootstrap 方法进行抽样和评估。在增广样本的过程中对a，b取不同值得到的样本分布如图3 所示。

图3 不同控制系数下的增广样本分布函数对比图Fig.3 Contrast of the expanding sample distribution function under different control coefficients

根据图3 可初步确定a=0.065，b=2 时增广得到的样本更加符合实际情况，因此将其作为评估的样本。Bootstrap 抽样样本量N=10 000时的对数均值和对数标准差的分布图分别如图 4 和图5 所示。由图中可看出，当样本量足够多时，对数均值和对数标准差的估计均接近正态分布。增广样本为：2.525 6，2.601 5，2.660 5，2.702 6，2.727 9，2.736 4，2.764 9，2.793 4，2.8019，2.827 2，2.869 3，2.928 3，3.004 2。

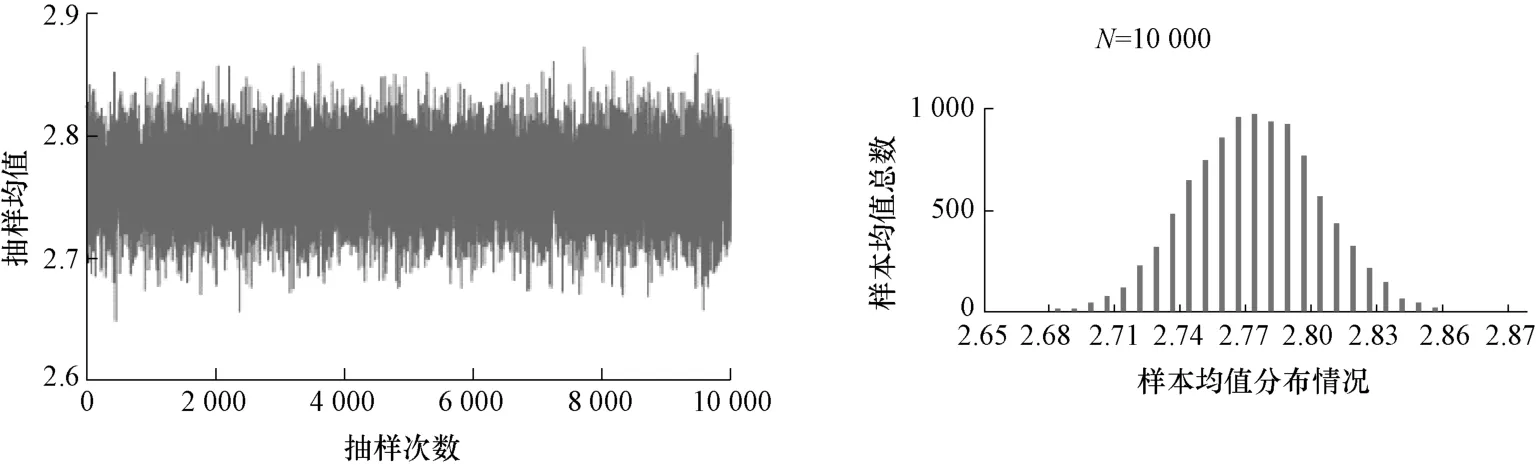
图4 Bootstrap 抽样时对数均值的频率分布图和直方图Fig.4 Frequency distribution and histogram of bootstrap sampling logarithmic mean

图5 Bootstrap 抽样时对数标准差的频率分布图和直方图Fig.5 Frequency distribution and histogram of bootstrap sampling logarithmic variance

综上所述，在确定对数均值和对数标准差的估计值后，根据任务寿命的可靠度计算式，带入Tlow= 2.530 7和T′=lg125= 2.096 9后，计算得到P′= 0.999 588。

2.4 极小样本方法对于钠泵部件的适用性对比分析

将三种计算方法进行对比如表1 所示。

表1 不同方法计算结果对比Table 1 Comparison of calculation results of different methods

从表1 中我们可看到虚拟增广+Bootstrap、综合概率法的分布密度函数中的可靠度函数和失效率函数的变化趋势基本一致，在一定范围内处于同一量级水平，故两种都具有一定的合理性。对于虚拟增广+Bootstrap 方法进行抽样和评估，其分析统计结果更加符合数据统计规律。从以上数据分析及概念来看，当以往类似件的试验估计信息与钠泵部件的相似度大时，采用半经验方法、综合概率方法评价两种方法进行分析更合理；当以往类似件的试验估计信息与钠泵部件的相似度不大时，采用虚拟增广+Bootstrap 方法进行评价更加合理。

3 结论

针对钠泵轴承的试验数据，验证了综合概率评价法和虚拟增广样本+Bootstrap 方法的适应性。综合概率分布评估法得到的部件综合概率密度函数更接近于真实的概率密度函数，精度相对较高；虚拟增广样本+Bootstrap 方法通过大量的抽样使数据更加贴合数据统计的原理，两种方法的分析结果为钠泵部件在极小样本情况下的可靠性评估提供了理论依据。同时，对钠泵部件极小样本的后续可靠性研究工作还需要做到以下两点。

（1）极小样本可靠性的评估重点是对类似部件的可靠性相关信息的收集，应注重相似部件的售后及维修情况的跟踪；

（2）对极小样本可靠性评估方法的确定，必须充分利用验前信息和本次试验的样本信息，才能给出精度相对高的可靠度评估结果。