正余弦函数不定积分计算方法探究

张海燕

（赤峰学院 数学与计算机科学学院，内蒙古 赤峰 024000）

不定积分计算是数学分析中的重要内容，通过不定积分熟练求出被积函数的原函数，可以为后面学习定积分打下基础。本文以数学分析中几类正余弦函数的不定积分计算为例，总结出不同类型积分的相关算法。

1 形如∫sinmxcosnxdx（m,n∈N）的不定积分

此类型的不定积分主要是利用“凑微分”即第一换元法计算，具体根据m,n奇偶性如下：

解(a)当m,n分别是一偶数和奇数时，不妨设n=2k+1,k∈N是奇数，则

当m,n分别是一奇数和偶数时，不妨设m=2k+1，则有

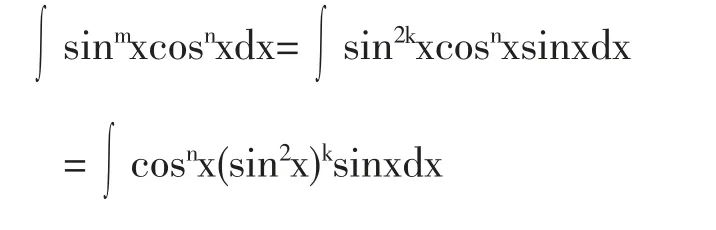
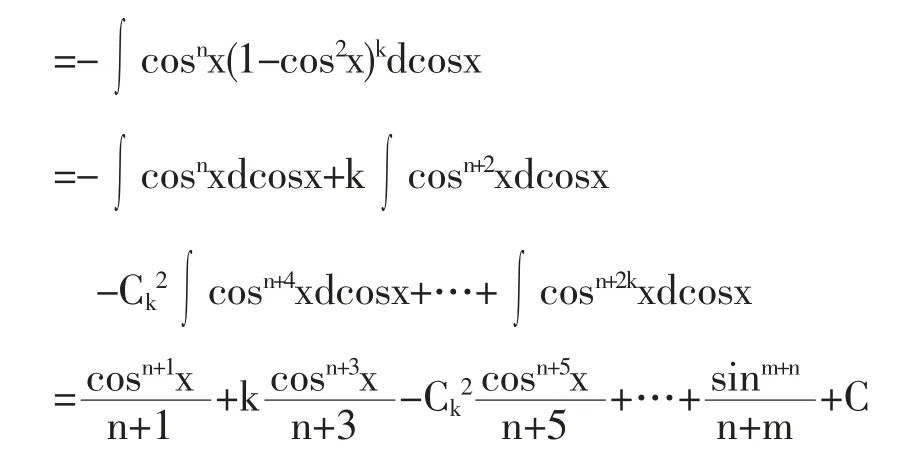
2 形如∫sinmxcosnxdx(m,n∈N)的不定积分

此类型的不定积分当m≠n时主要用积化和差公式，将乘积型的不定积分化成正余弦函数和或差的不定积分，m=n是利用凑微分计算。

3 利用万能公式计算的不定积分

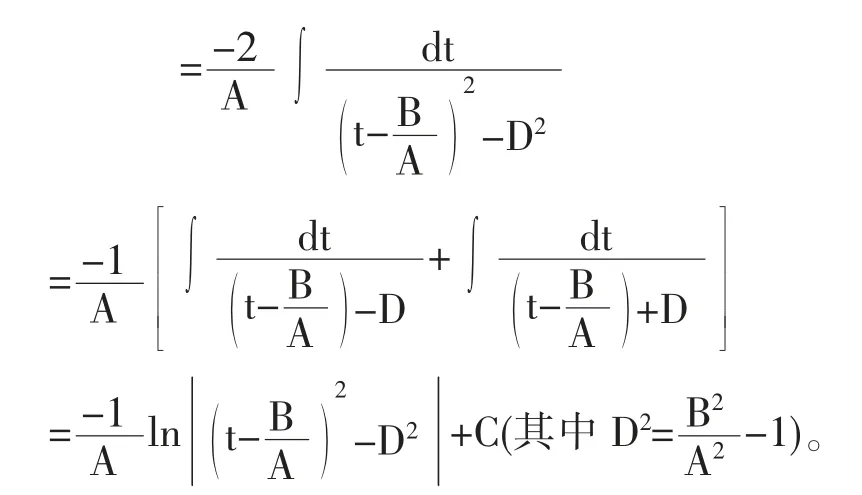
4 利用sin2x+cos2x=1计算的不定积分

5 结束语

通过以上几类正余弦函数不定积分的计算，我们得到了相关公式，关于正余弦函数不定积分的计算有些题目需要将不同方法融合起来。初学者一定要多加练习，总结解题规律，做到举一反三，融会贯通。