基于延时陷波算法的车内主动噪声控制

杨忠礼，卢炽华，刘志恩，陈 弯

(1.武汉理工大学现代汽车零部件技术湖北省重点实验室，湖北武汉 430070；2.汽车零部件技术湖北省协同创新中心，湖北武汉 430070)

0 引言

现代汽车发动机功率不断上升，汽车平均车速不断增加，车内噪声问题日渐突出，成为评价汽车乘坐舒适性的重要指标[1]。车内中、高频噪声可通过吸声、隔声、隔振等传统被动降噪措施得到有效抑制，而低频噪声具有穿透力强且衰减缓慢的特点，仍然采用被动噪声控制意味着车身质量、尺寸与制造成本大幅增加，是不可取的[2]。主动噪声控制(Active Noise Control,ANC)技术基于声波相消干涉原理，控制次级声源产生与初级噪声幅值相同、相位相反的抵消声波，在目标区域实现噪声消除，该技术弥补了被动噪声控制技术在低频噪声控制中的不足[3-4]。

特别是汽车发动机的阶次噪声主要集中在低频范围，且具有确定的频率信息，ANC作为车内噪声控制的一项有效措施已被成功应用[5-8]。

本文在FxLMS(Filtered-x Least Mean Square)算法自适应陷波窄带ANC系统的基础上，提出一种改进的自适应陷波方案。方案采用参考信号与滤波参考信号数字合成，克服了原有延时陷波算法采用次级通路延时简化模型所引入的相位误差。仿真与试验结果均表明，所提方案对稳态与非稳态工况下的车内窄带噪声均具有较好的控制效果。

1 自适应陷波窄带ANC系统

1.1 FxLMS算法自适应陷波窄带ANC系统

自适应陷波器自适应调整两个权系数来对正弦、余弦参考信号进行加权求和，从而得到抵消信号，用于窄带ANC系统时表现出了良好的降噪性能，同时可以将多个自适应陷波器并联以消除初级噪声中的多个窄带分量[9-11]。图1为并联自适应陷波窄带ANC系统的原理框图，其中xm，0(n)和xm，1(n)分别表示余弦、正弦参考信号，d(n)表示初级噪声信号，e(n)表示残余误差信号，S(z)为次级通路传递路径，包括：数模转换器、功率放大器、次级扬声器、误差传声器、模数转换器等电子器件的电通路以及次级扬声器至误差传声器之间的声通路，表示对S(z)的估计。

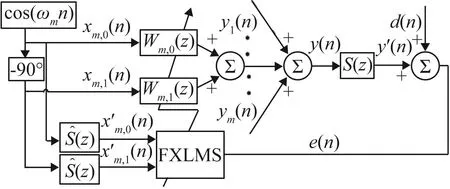
图1 自适应陷波窄带ANC系统Fig.1 Principle diagram of the narrowband ANC system with active notch filter

在该系统中，自适应陷波器的权系数迭代过程如下：

(4)基于FxLMS算法利用最小均方准则更新自适应陷波器权系数，于是有：

式中：μm为步长因子。经过多次迭代后，系统收敛，残余误差信号e(n)达到最小值，完成对频率分量ωm的消除。

1.2 次级通路离线建模

次级通路离线建模在ANC系统工作之前完成对次级通路的识别。当认为次级通路满足线性时不变假设时，使用离线建模既能获得较高的建模精度又能大大减小后续的计算复杂度[12]。图2为使用附加随机噪声法，利用FIR滤波器完成次级通路离线建模。

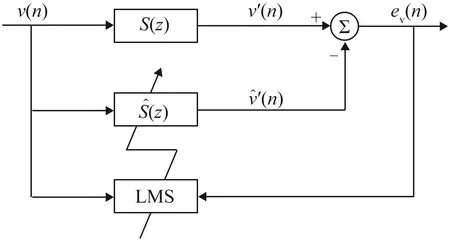
图2 次级通路离线建模Fig.2 Off-line modeling of the secondary path

(1)白噪声v(n)作为次级声源激励信号和建模参考信号，v(n)经实际次级通路滤波后的信号v'(n)作为期望信号由误差传声器获取，于是有：

式中：V(n)=[v(n)v(n-1)...v(n-L+1)]T为白噪声信号向量，是长度为L的脉冲响应向量。

(2)基于LMS算法，得到Ŝ(n)的迭代公式为

式中：μs为次级通路建模滤波器的步长因子。

自适应陷波器虽然较传统自适应滤波器结构更简单，但为了获得滤波参考信号以补偿次级通路的影响，参考信号同样需要与次级通路的脉冲响应估计进行卷积运算，而为了反映次级通路在整个待消声频率范围内的频率特性，通常具有较大的阶数L，且当待抵消频率的个数M增加时，由长向量卷积运算所引入的计算量将更加巨大，因此算法需要更多的改进。

2 次级通路简化模型分析与改进

考虑线性时不变系统的频率不变性，次级通路对正弦输入信号的响应仅仅与次级通路在其频率ωm处的幅频特性及相频特性有关。因此在窄带ANC系统中，离线建立的次级通路模型只需准确反映次级通路在待抵消频率处的幅值和相位即可[13-15]。延时陷波算法将次级通路简化为在各个频点上的纯延时模型，即=z-Dm，Dm表示在频率ωm处对应的延迟点数。从而，在1.1节中由式(4)获得滤波参考信号时，次级通路与参考信号之间的卷积运算可简化为单纯的样本延迟，相应地，式(5)中的权系数迭代公式可简化为

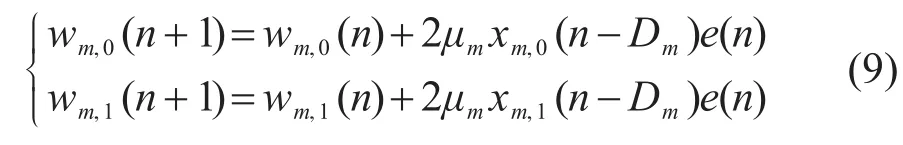
具体应用时，建模得到次级通路脉冲响应的离线估计后，对进行傅里叶变换得到次级通路的相频特性。实际情况下，输出信号的相位总是滞后于输入信号的相位，相频特性全为负值，但变换后相频特性的值域为[-π，π]，又因参考信号具有周期性，可将相频特性中所有大于0的部分减去2π，得到值域为[-2π，0]的新相频特性φ(ω)。进而，次级通路对参考信号的延迟点数Dm可以描述为

式中：round(·)表示就近取整函数，即可得到次级通路延时在采样周期上的估计。由于次级通路的幅频特性对ANC系统的影响可以通过调整步长进行补偿，而相频特性对系统的降噪效果有主要影响，因此下面对次级通路延时简化模型中的相位关系进行分析。

2.1 次级通路延时简化模型相位分析

在传统的延时陷波算法中，对次级通路进行延时估计，由次级通路引入的延时被估计为采样周期的整数倍，而当待抵消频率增大，参考信号在单个周期波形内的采样点数减少，导致由延时估计所带来的相位误差增大，由此产生的相位误差被认为是延时陷波算法的主要缺陷之一[16]。表1给出了采样率为2 000 Hz时，各频率时域波形相邻两采样点之间的相移与采用次级通路延时估计将引入的相位误差。

表1 采样率为2 000 Hz时的相移与相位误差Table 1 Phase shift and error at the sampling rate of 2 000 Hz

在基于系统识别方法的次级通路离线建模过程中，一定量的相位误差已不可避免，而延时估计所带来的额外相位误差进一步恶化了ANC系统的性能。次级通路建模时的相位误差会导致最大步长因子的减小和降噪性能的下降，为系统设置较大的步长、较小的相位误差即可导致系统发散[17-18]，设置较小的步长可以使系统承受一定的相位误差，达到收敛，而这又与期望系统具有较快的收敛速度相矛盾。

因此，本文针对延时陷波窄带ANC系统的现有缺陷，提出同时进行参考信号与滤波参考信号数字合成的解决方案，用于改善延时陷波窄带ANC系统在相位精度方面的性能。

2.2 参考信号与滤波参考信号数字合成

自适应陷波器跟踪的是参考信号频率，参考信号与滤波参考信号的特征对于窄带ANC系统的降噪性能有着直接影响。查表法是一种简单易行的正弦波数字合成方法，该方法需读取一系列事先存储的数据样本。图3给出了利用查找表同时生成自适应陷波器所需正弦、余弦参考信号及两者对应滤波参考信号的方法。

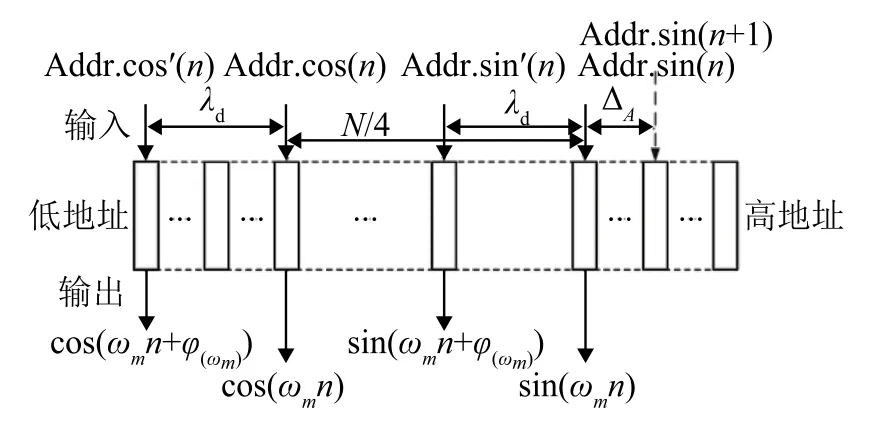
图3 利用查找表生成参考信号与对应的滤波参考信号Fig.3 Reference signals and the corresponding filtered reference signals generated by look-up table

(1)查找表中存有一个完整正弦波形的N个样本值，相邻样本值之间的角度以弧度记为ω0=2πN，样本值的计算方法为

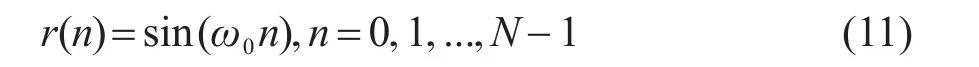
(2)当前时刻同一频率的正弦、余弦参考信号及滤波参考信号在查找表中的地址分别表示为Addr.sin(n)、Addr.cos(n)、Addr.sin'(n)、Addr.cos'(n)，并且两相邻采样时刻的查找表地址递增量记为ΔA，如图3所示，则产生信号的频率ωm仅与ΔA有关，对于确定的ωm，ΔA的表达式为

(3)同一时刻参考与滤波参考信号地址之间存在一个差值λd，并且随着参考信号的频率变化而变化。这个差值作为次级通路的替代模型同样存储在一个查找表中，不同的是λd只体现了次级通路在相位上的特征。λd与第2节中的相频特性φ(ω)有以下关系：

通过多组具有不同ΔA的地址循环索引查找表可以产生多个频率的正弦波，同时随时间变化的ΔA可以产生时变频率的正弦波，适用于窄带ANC系统中的非稳态工况。

由上述分析可知，所提方案独立地生成参考信号与滤波参考信号，参考信号与滤波参考信号之间的相位估计误差不再随参考信号频率增大而增大，而是保持定值。例如，N取8 192，此时相位估计误差在全频段保持为0.02°，较表1中各频点下的相位估计误差有很大的改进，同时，仅带来额外的少量存储器资源消耗。

2.3 改进的延时陷波窄带ANC系统方案

图4为使用所述方法的延时陷波窄带ANC系统，系统使用声学或非声学传感器获取与初级噪声具有强相关性的参考信息。这些参考信息不直接包含频率信息，因此增设一个传感器信号预处理模块来获取初级噪声频率信息。

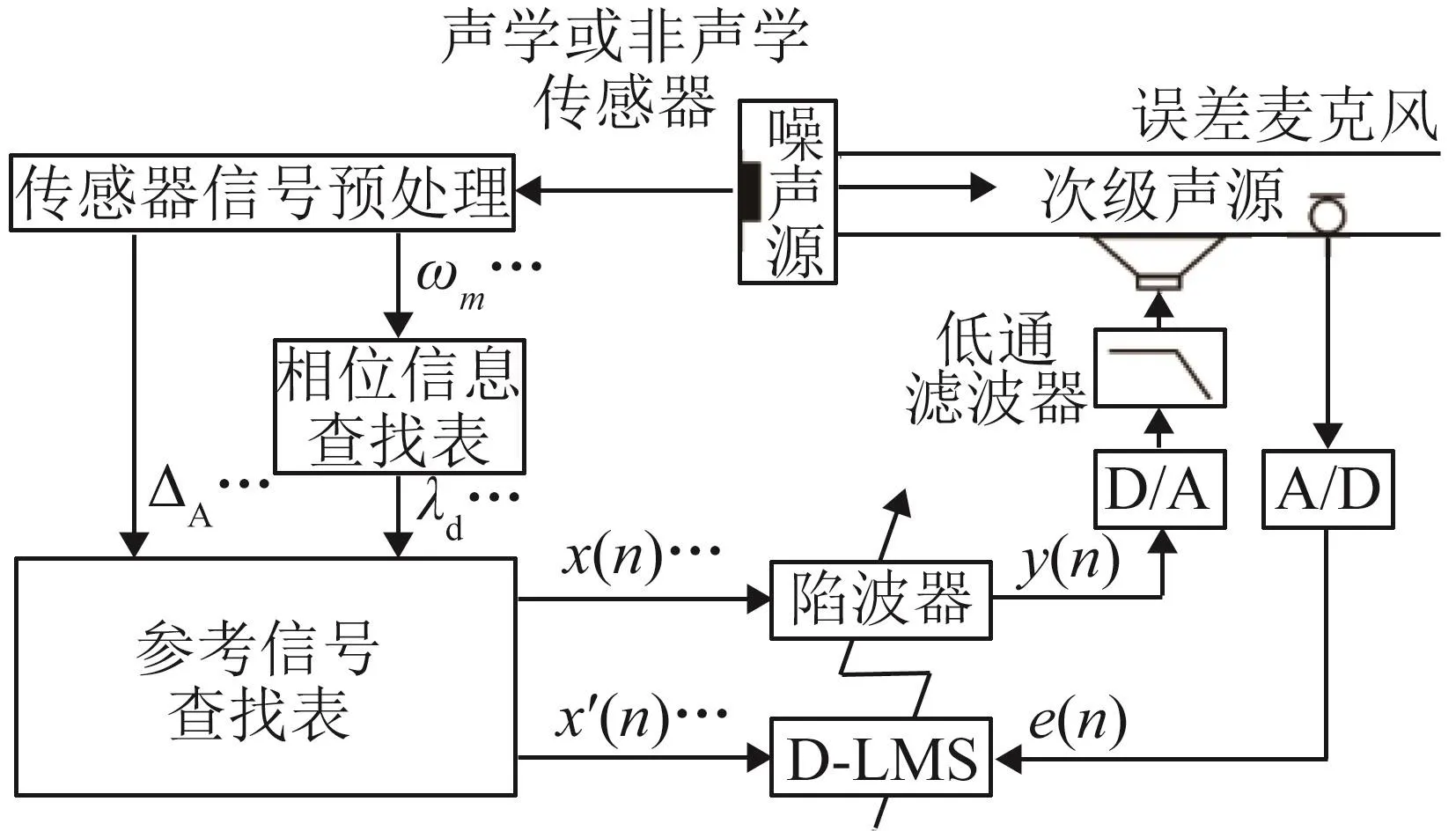
图4 延时陷波窄带ANC系统Fig.4 Principle diagram of the delayed notch algorithm based narrowband ANC system

在获得初级噪声频率信息后，计算对应的ΔA，同时索引相位信息查找表得到λd，最后索引正弦波查找表生成参考信号、滤波参考信号，输入自适应陷波器中完成迭代计算。由内部生成参考信号的延时陷波窄带ANC系统，较使用参考传声器的前馈ANC系统避免了次级声源的声反馈与参考传声器老化带来的非线性，独立地控制每一个谐波分量，具有广泛的适用性。

3 仿真与对比分析

3.1 系统仿真

在LabVIEW软件中，使用上述方案建立了单通道的延时陷波窄带ANC系统模型，针对多谐波目标噪声进行降噪性能仿真分析。仿真参数设置如下：初级噪声为三个不同频率的正弦波叠加，频率为f1，f2，f3分别为 80，160，240 Hz，幅值 A1，A2，A3分别为0.3，0.05，0.025 Pa，对应的声压级分别为80，65，59 dB，同时加入信噪比为20 dB的白噪声模拟额外加性随机噪声；正弦波查找表长度N取为8 192；仿真时间为10 s；采样率为4 096 Hz；步长因子取0.005。由于真实的次级通路是未知的，仿真过程中使用离线建模得到的次级通路脉冲响应作为真实次级通路。

仿真结果如图5、6所示。从图5可以看出，ANC系统在0.1 s开启后，残余噪声迅速减小，初级噪声中的正弦成分被明显削弱，残余噪声保持在较小值。图6为控制前后噪声信号的功率谱对比，可以看到此时ANC系统等效于一个陷波器，初级噪声在80，160，240 Hz处的峰值被完全消除，主动噪声控制效果明显。图5和图6的结果充分证明了延时陷波算法对窄带周期性噪声具有优异的降噪性能。

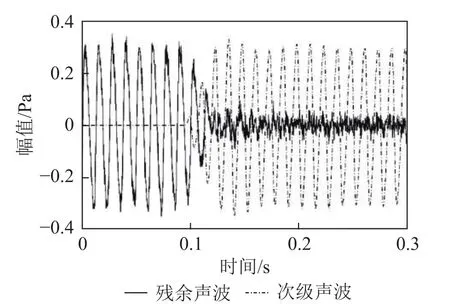
图5 残余噪声瞬时声压Fig.5 Instantaneous sound presure of residual noise

图6 残余噪声功率谱Fig.6 Residual noise power spectrum

3.2 运算量对比分析

运算量是ANC系统的一项重要评价指标，ANC系统中运算量主要来源于三部分：次级通路对参考信号的滤波运算，滤波器的输出运算，自适应算法的迭代运算。当以上三部分的总运算时间超过系统的采样周期时，系统失效。表2给出了三种不同类型的ANC系统在工作期间计算每个输出样本所需的运算量。

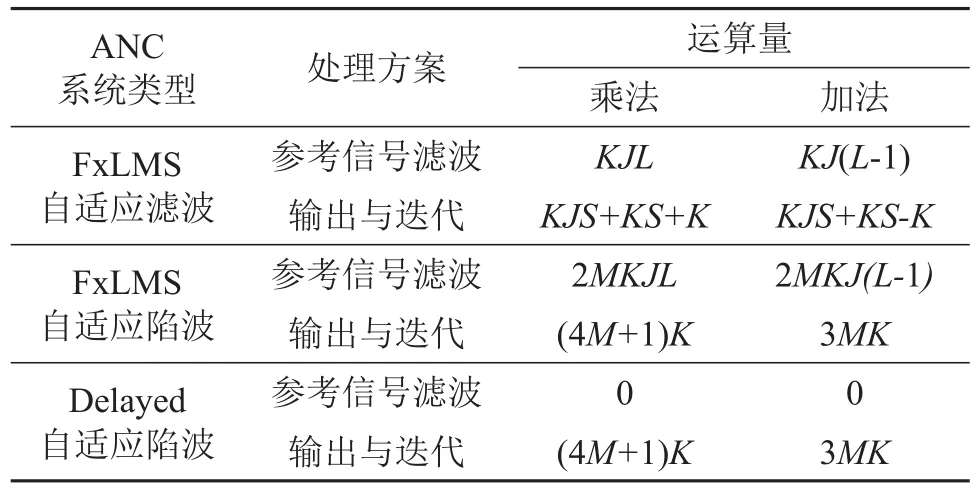
表2 三类不同ANC系统运算量比较Table 2 Comparison of computational complexity between three different ANC systems

从表2中可以看到，使用FxLMS算法自适应滤波器的ANC系统除了参考信号滤波运算量大以外，由于使用高阶的自适应滤波器，在输出与迭代计算过程中又引入了极大的运算量；FxLMS算法自适应陷波器在输出与迭代过程中的运算量已有较大改善，但随着待控制频率数目的增加，正弦、余弦参考信号过多又引起次级通路对参考信号的滤波运算量增加，这部分运算量同样不可忽视；延时自适应陷波器通过次级通路的延时信息生成滤波参考信号，完成次级通路对参考信号在相位上的等效滤波，大幅减小次级通路带来的运算量，同时继承了自适应陷波器在输出与迭代运算过程中运算量小的优势，大幅降低了对微控制器的算力要求。

4 试验设计

CompactRIO是美国NI公司开发的一套基于现场可编程门阵列(Field Programmable Gate Array,FPGA)的便携式数据采集系统，配合多种类的I/O模块，提供快速灵活的测控解决方案。因此本文选用CompactRIO 9040编程控制器、8通道模拟输入NI 9231板卡、4通道模拟输出NI 9269板卡、GRAS 46AE传声器等硬件设备完成了试验台架的搭建，同时在LabVIEW开发环境下，利用Lab-VIEW Real-Time Module与LabVIEW FPGAModule工具包完成了次级通路辨识与主动降噪程序的编写工作，建立了改进的车内双通道延时陷波窄带ANC系统，用于改善主副驾驶的声学环境。

所建系统将2个额外的低音音响置于车门处，模拟车门扬声器来作为次级声源。主、副驾驶头枕部位分别记为测点一、测点二，两测点各布置两个传声器，其中误差传声器用于获取残余噪声进行控制算法的迭代更新，监测传声器用于记录残余噪声水平，同时通过发动机点火脉冲信号测量发动机转速，由此获取初级噪声频率信息，系统布置如图7所示。

图7 实车延时陷波窄带ANC系统Fig.7 Photo of the delayed notch algorithm based narrowband ANC system in vehicle

试验准备阶段，在车窗全封闭的条件下完成次级通路的辨识工作，辨识过程使用均值为0、方差为0.034的平稳高斯白噪声作为激励信号，得到4组长度512阶的次级通路脉冲响应估计，如图8所示，其中L表示主驾驶侧，R表示副驾驶侧，“LR次级通路”表示主驾驶侧扬声器至副驾驶侧误差传声器的次级通路估计，其余次级通路估计同理。对次级通路的估计滤波器进行2.2节中的离线处理，并将获得的差值信息λd上传至相位信息查找表中，同时建立一个长度为8 192的正弦波查找表，用以生成参考信号与滤波参考信号。

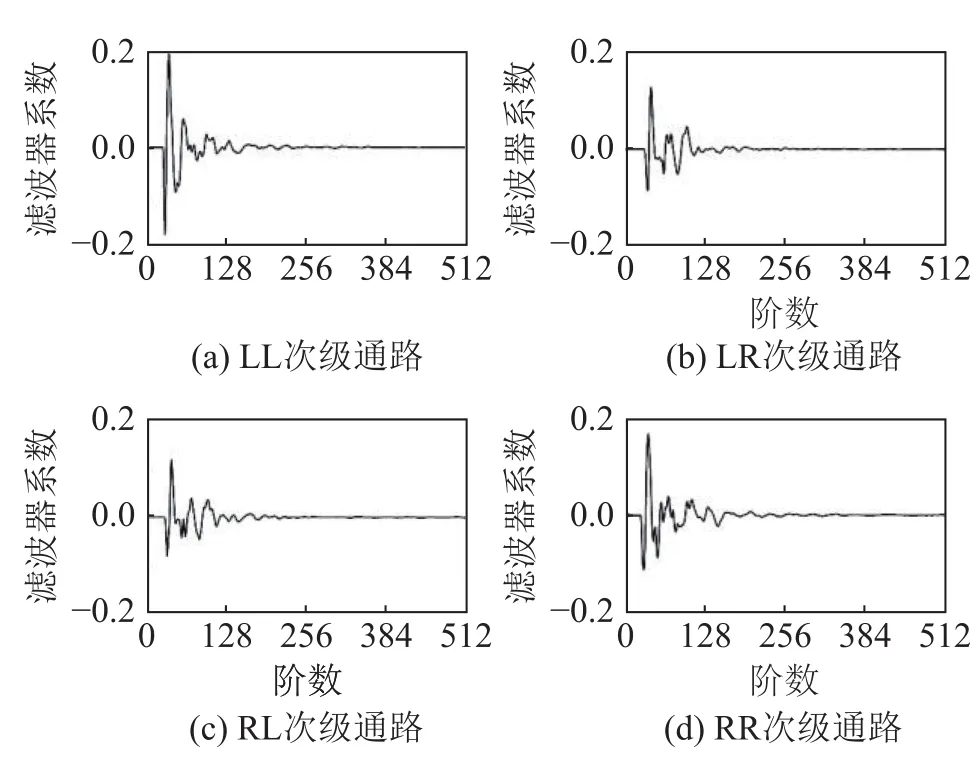
图8 次级通路单位脉冲响应估计Fig.8 Estimation of unit impulse response in secondary path

由于所选试验车辆内发动机的2阶、4阶噪声较明显，因此在试验过程中以发动机2阶、4阶噪声为控制对象，进行了车辆定置发动机定转速与行驶过程急加速两种工况下的主动噪声控制试验。

4.1 定转速工况

定转速工况下发动机转速为3 500 r·min-1，测试时长为10 s，采样率为4 096 Hz，步长因子取0.004。图9为窄带ANC系统开启前(ANC-ON)、后(ANC-OFF)车内噪声时域信号的部分波形。如图9所示，在5.3 s附近ANC系统开启后，两测点的声压幅值均大幅下降，残余噪声迅速收敛至较小值，并保持稳定。

图9 两个测点的车内噪声信号Fig.9 Vehicle interior noise signals at two measuring points

为探究ANC系统对发动机2阶与4阶噪声的实际降噪效果，对两测点的噪声信号进行频谱分析，所得功率谱如图10所示。

图10 两个测点的车内噪声功率谱Fig.10 Vehicle interior noise power spectrums at two measuring points

定转速工况下，实际的2阶与4阶噪声峰值分别出现在117 Hz与234 Hz处，此时对应的发动机转速为3510r·min-1。ANC系统开启后，主驾驶测点处2阶、4阶噪声峰值分别下降23.74、10.50 dB(A)，副驾驶测点分别下降22.55、12.71 dB(A)，且系统对车内原初级噪声在2阶、4阶以外的其他峰值频率点的影响较小。

根据发动机定转速工况下的试验结果，延时陷波算法对发动机定转速下的车内阶次噪声具有良好的降噪性能，与3.1节中的仿真结论相符。但对发动机的2阶、4阶噪声降噪效果存在明显差异。发动机2阶噪声的原峰值较大，所以对2阶噪声的控制效果明显优于原峰值较小的4阶噪声。此时车内噪声仅包含发动机噪声，测试结果可看作此ANC系统在车内环境下的理想降噪性能。

4.2 急加速工况

急加速工况时，车内噪声随发动机转速变化快速变化。急加速工况是典型的非稳态工况，可用于考察此ANC系统对时变噪声的跟踪性能。选用汽车3档下的全油门加速工况作为测试工况，发动机转速由1 600 r·min-1升至4 800 r·min-1，加速时间约为12 s。此时车内除了发动机噪声还包括路噪、风噪等行驶噪声，能够真实反映实际使用条件下此ANC系统的降噪性能。

自适应陷波器在初级噪声时变的情况下通常无法完全收敛到当前频率的最佳值即开始进入下一频点的迭代，因此非稳态过程中的降噪效果更多地取决于系统的收敛速度，而步长因子是影响收敛速度的主要因素。试验过程中采用试错法对步长进行了简单的标定，为系统设置较大的步长，系统稳定性下降；设置较小的步长，稳定性增强但加速过程中的降噪效果有所下降，最终设置的步长在0.002～0.004之间，既能保证系统的稳定性又对时变噪声具有较好的跟踪能力。

从图11、12中可以看出，ANC系统开启前，车内发动机2阶、4阶噪声明显，且2阶噪声对车内噪声的贡献量较大；ANC系统开启后，阶次噪声明显减弱，但仍能在色彩图上看到阶次线，说明ANC系统的降噪性能未充分发挥。同时，不同转速下ANC系统对同一阶次噪声的降噪效果存在差异，在阶次噪声明显的转速范围内系统的降噪效果更明显；不同测点的降噪效果也存在细微差别，副驾驶测点的降噪效果略优于主驾驶测点。对降噪前后的乘员耳旁噪声进行阶次分析，结果如图13所示。从图13(a)可以看出，原车内总声压级在发动机3 000 r·min-1以上时出现大幅上升，总声压级与发动机转速的线性度较差，ANC系统开启后，两测点的总声压级在“隆起”的转速范围内均明显下降，主驾驶测点最大降噪量出现在3 850 r·min-1处，下降8.45 dB(A)，副驾驶测点最大降噪量出现在3 600 r·min-1处，下降8.46 dB(A)，同时车内声压级对发动机转速的线性度明显改善，符合人们对车内声品质的基本要求。

图11 ANC控制前后测点一的噪声频谱Fig.11 Frequency spectrums before and after noise control at the measuring point 1

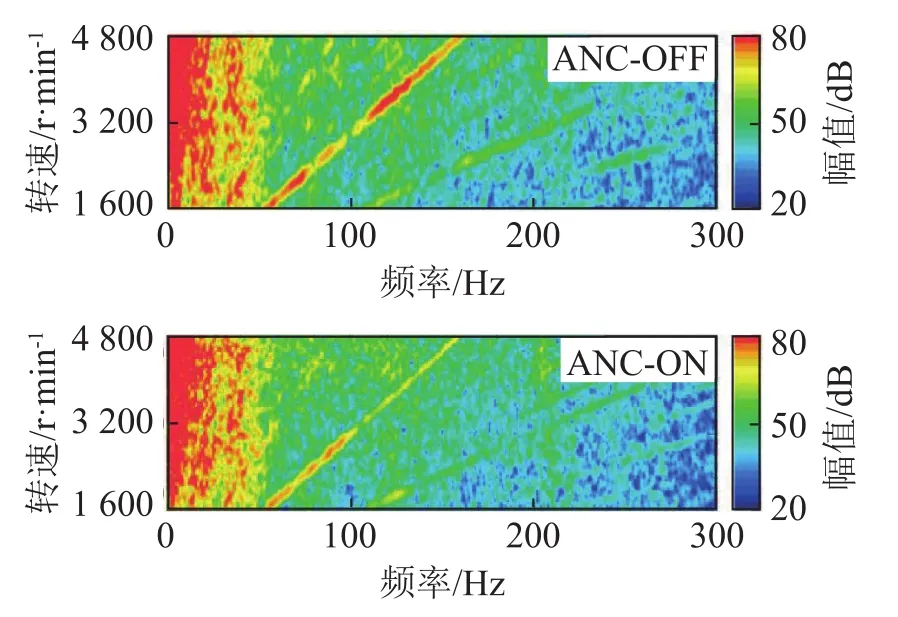
图12 ANC控制前后测点二的噪声频谱Fig.12 Frequency spectrums before and after noise control at the measuring point 2

耳旁噪声的各阶次成分如图13(b)所示。发动机2阶噪声对车内原初级噪声的贡献量较大,在绝大多数转速范围内，系统对2阶噪声的降噪量明显，主、副驾驶测点的2阶最大降噪量都出现在3 700 r·min-1附近，均在 16 dB(A)以上，与图 11、12分析结果相符。但在2 400～3 000 r·min-1时，车内原2阶噪声在幅值上出现了大幅“凹陷”，此时系统控制后的2阶噪声反而增加，引起总声压级略微增加。这是受当前步长条件下系统跟踪性能的限制，后续应选择更加合适的步长或采用变步长规则进行改善。图13(c)中，发动机4阶噪声对车内原初级噪声的贡献量较小，仅在部分转速下存在峰值，同时4阶噪声频率随转速的变化较2阶噪声更为迅速，控制难度上升，在ANC系统开启后4阶噪声的峰值同样得到有效控制。试验结果表明，本文所建窄带ANC系统实现了对车内发动机阶次噪声的有效控制。

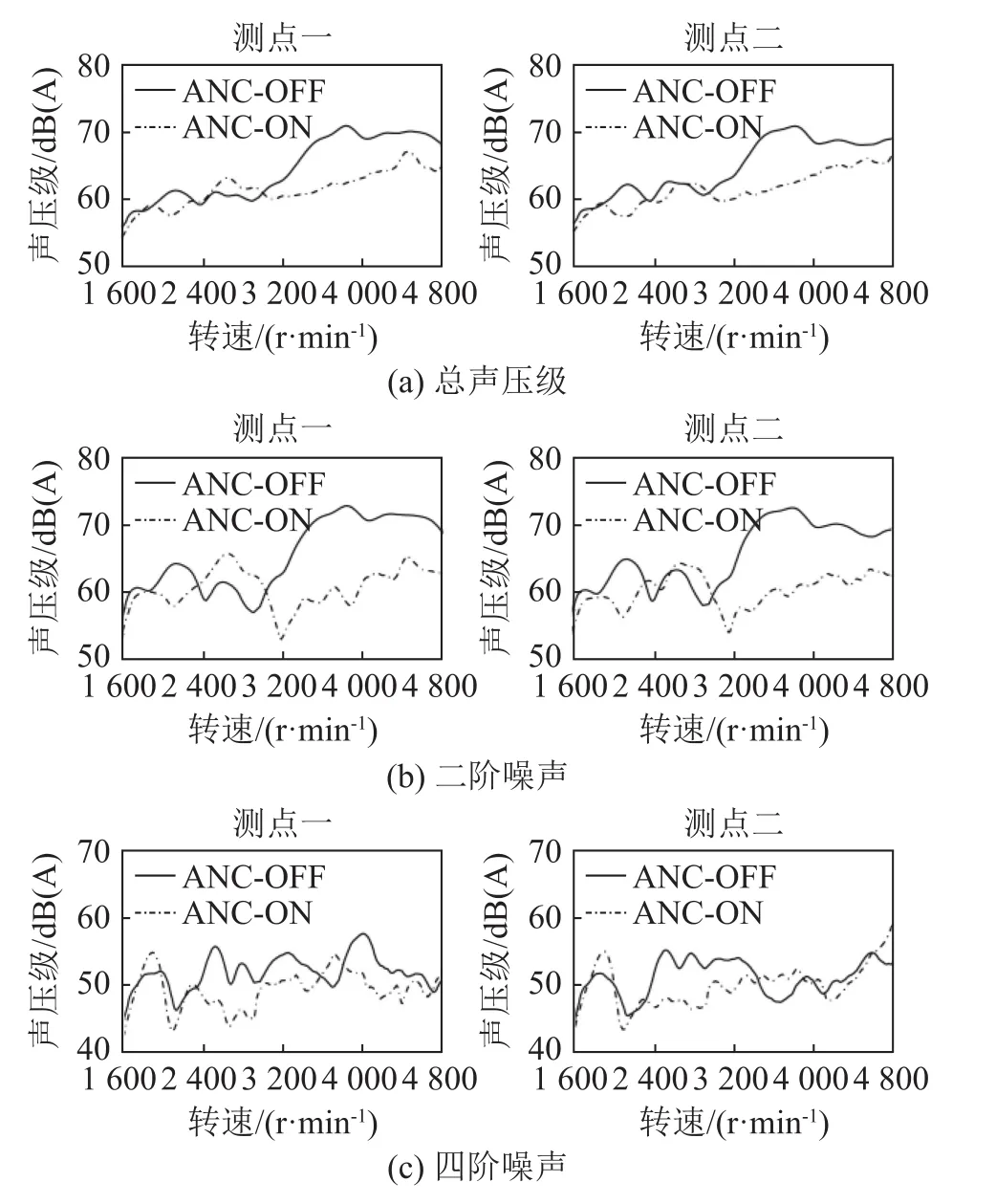
图13 两个测点的车内噪声总声级及2阶和4阶声级的分析结果Fig.13 Analysis results of total sound level and the Order 2 and Order 4 sound levels of the vehicle interior noise at two measuring points

5 结论

本文研究了自适应陷波算法在车内噪声主动控制中的应用，建立了使用延时陷波算法的车内主动噪声控制系统，从理论分析与试验研究论证了系统的有效性。理论分析表明延时陷波算法在很好抑制窄带噪声的同时，较传统的FxLMS自适应滤波算法，显著降低了计算量，适用于简单和低成本的微控制器，具有广泛的应用前景；试验研究发现在发动机定转速工况下，系统对发动机2阶、4阶噪声的最大降噪量达到23.74、12.71 dB(A)，在非稳态工况下，系统仍具有优异的降噪性能，两测点总声压级的最大降噪量分别达到8.45、8.46 dB(A)。在后续工作中，为进一步提升系统性能，一方面有必要对初级噪声频率与幅值变化以及步长因子对系统在非稳态工况下的降噪性能影响进行探讨；另一方面应对车内源噪声的阶次构成进行分析，关注阶次噪声突出的转速范围，有选择性地进行控制，进一步改善车内声品质。