基于NSGA-Ⅱ的光导注塑成型工艺参数多目标优化
2022-10-17刘安林
刘安林,王 钊
(1. 西安航空职业技术学院航空材料工程学院,陕西 西安 710089;2. 江苏大学机械工程学院,江苏 镇江 212013)
0 引 言
光导是一种把光源按照预设轨迹导向将要发光位置的结构件[1],因其具有寿命长、造型美观、安全性高、绿色健康等特点,而被广泛应用于汽车、建筑、景观等行业。然而,光导作为透明光学元件,对成型质量要求较高,给制造技术带来了挑战。目前成型透明光学元件的主要方法包括3D打印技术和注塑成型技术。3D打印技术成本较高,不适合批量生产,因此多以注塑成型技术为主。目前,人们对透明光学元件的成型技术也有了一定的研究。沈洪雷等[2]利用高频压电陶瓷致动技术,在模具内部形成弹簧与电场共同震荡的效果,用于调节熔体的填充、保压过程,以获得致密的塑件。贺圣彦等[3]以产品收缩和翘曲为目标,利用正交实验寻求最佳工艺参数组合,最终获得质量良好的产品。许俊豪等[4]将塑件进行分层处理,通过两次注塑成型得到厚壁塑件。
本文以一种光导为例,基于Moldflow进行仿真分析,利用最优拉丁超立方抽样方法,构造Kriging模型,最后探究了各个工艺参数对产品成型质量的影响。
1 塑件成型工艺性分析
1.1 结构分析
光导主要是利用光的反射、折射和全反射规律进行设计的。当光从光密介质射入到光疏介质,且入射角大于等于某一临界角度时,只发生反射光线,不发生折射的现象称为全反射,其原理如图1所示[5]。当光沿AO1或AO2传播时,既可以接收到反射光线也可以接收到折射光线;当光沿AO3入射或大于该临界角时,将只接收到反射光线,这样光将沿着光导管传播下去[6]。为了使得光从光导管侧面射出,就需要设计新结构,打破全反射光路,其结构如图2所示。当光在AB面上发生第一次全反射以后,分别在O4、O5处再发生一次全反射,最终在O6、O7处发生折射,在光导管侧面接收到光信号。因此在光导管底部设计成锯齿形状,如图3(b)所示,用于破坏全反射光路,达到侧面出光的效果。
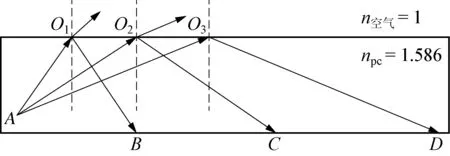
图1 全反射光路
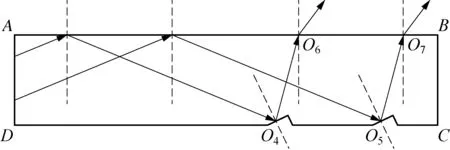
图2 光导原理图
图3为某光导产品数模结构,其轮廓形尺寸为:40.38 mm×351.97 mm×100.02 mm,最大壁厚10.25 mm。外观呈长条形,顶部出光部分光滑过渡,为G4连续,底端呈锯齿状,主要起到反射光路的作用。采用注塑成型方法成型该产品,材料为SABIC公司生产的牌号为Lexan 141R的PC塑料,密度为1.19/cm3,收缩率为0.50%。光导作为光学元件,要求外观透明,表面质量良好,不允许有气泡、缩痕、飞边等缺陷,尺寸波动较小,否则影响出光效果。
1.2 数值模拟
将3D数模导入Moldflow并进行网格划分,设置成3D网格,以便更好地模拟厚壁塑件成型过程。选择材料牌号为Lexan 141R,成型工艺为“充填+保压+翘曲”。为了保证分子取向一致,减少熔接痕和翘曲变形,浇口位于塑件末端,如图4所示。根据Moldflow推荐的参数进行分析:注射时间为1.6 s,熔体温度320℃,保压压力为10 MPa(后续以压力百分比表示),模具温度100℃,保压时间为20 s。得到塑件的翘曲量为2.324 mm,收缩率为12.04%,如图4所示。
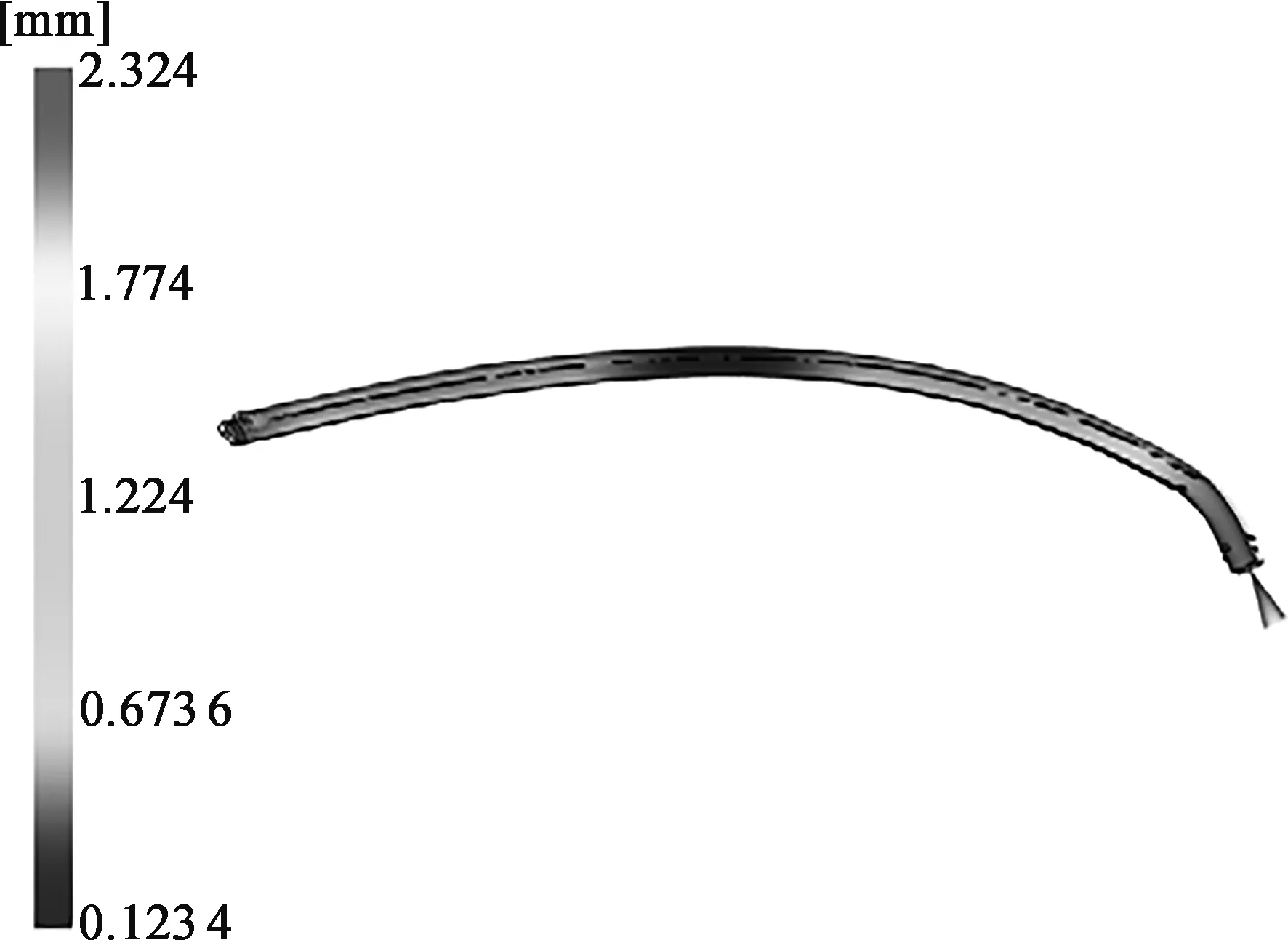
(a) 翘曲变形量
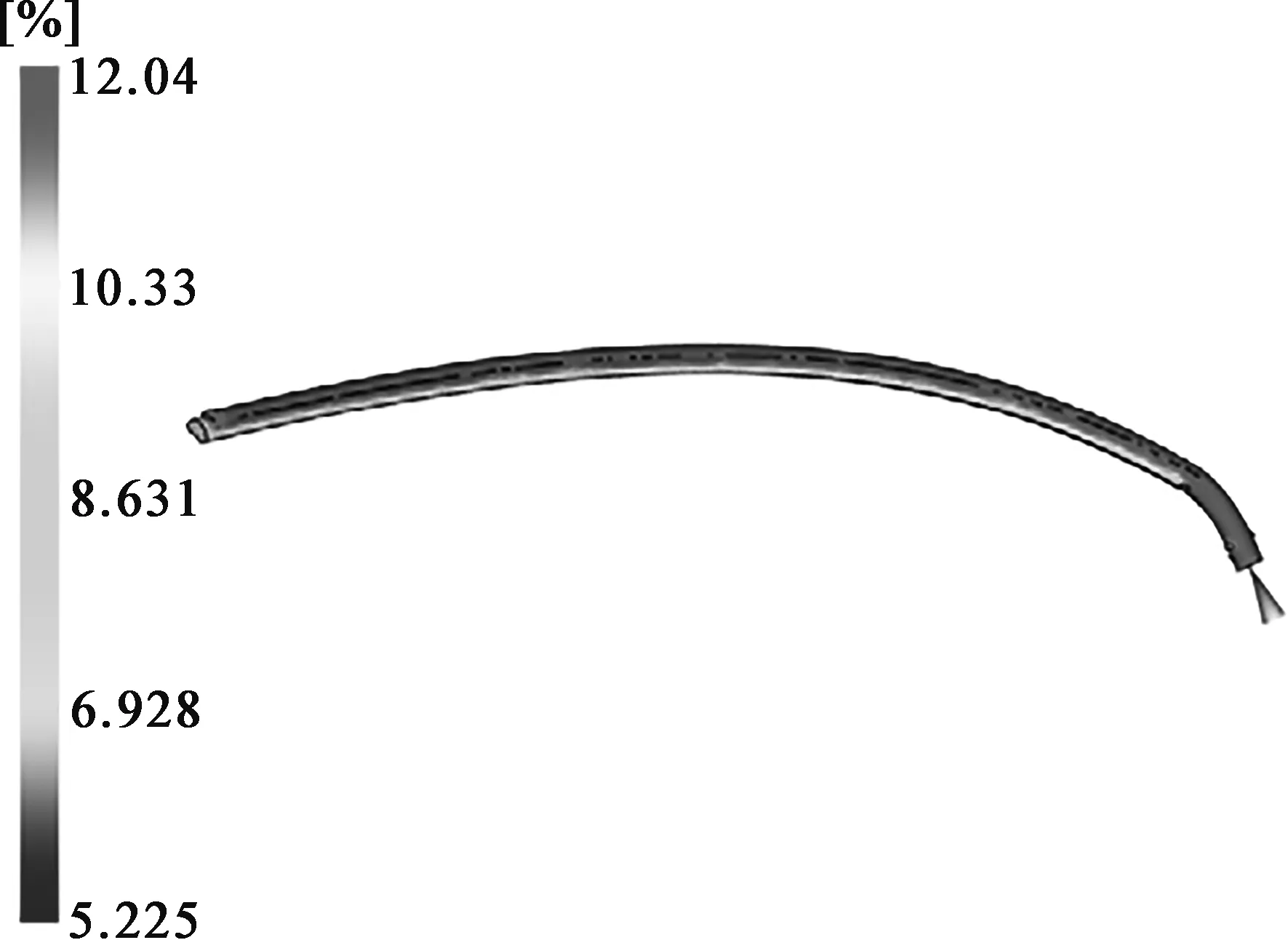
(b) 体积收缩率
2 试验结果与讨论
2.1 试验设计
试验设计属于数理统计领域的内容,是解决工程优化问题的有效途径之一。本文选择最优拉丁超立方设计试验,相比其他方法,可以使抽取的样本更加均匀,保证因子与响应值的拟合更加趋于实际情况。其原理是将m维空间均分成n个区域,再从每个区域中抽取1个样本点,构成m维n个样本的设计[7]。
成型光导时,工艺参数对成型质量起着决定性作用,因此需要合理设置成型参数值。以注射时间(A)、模具温度(B)、熔体温度(C)、保压压力(D)和保压时间(E)为设计因子,各因子取值范围如表1所示。以翘曲变形量(X)和体积收缩率(Y)为响应值,利用最优拉丁超立方设计40组实验,试验方案及结果见表2。根据表2信息,建立Kriging模型,研究各因子对响应值的影响规律。
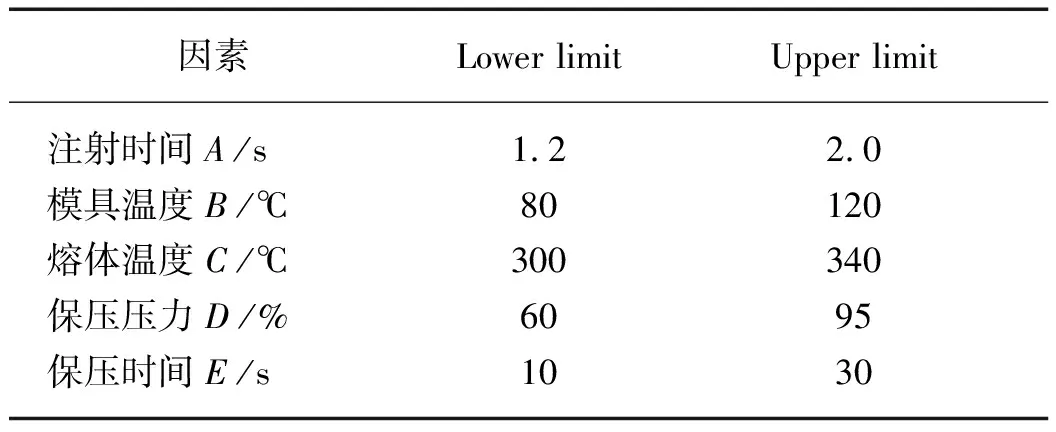
表1 试验因素及取值范围
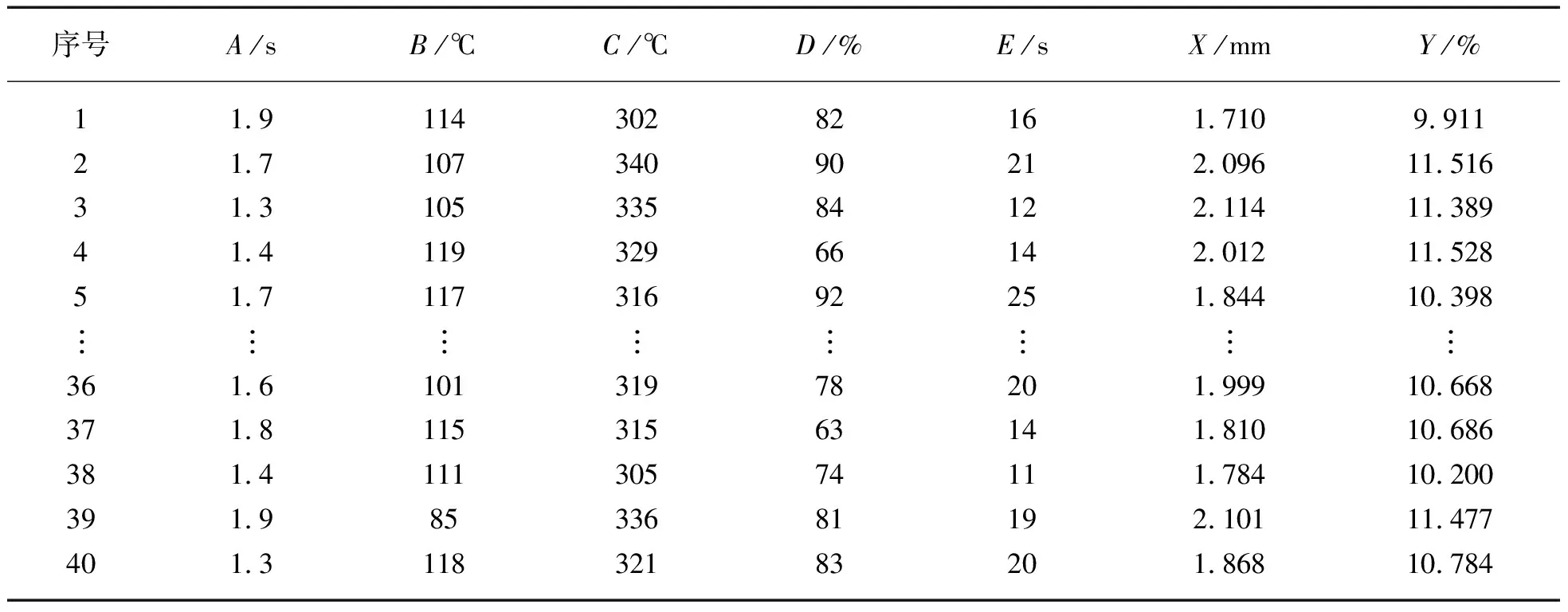
表2 试验方案及结果
2.2 Kriging代理模型的建立及精度检验
各因子具有不同量纲,建立模型时选用向异性,以Gaussian函数拟合模型,所得评价指标见表3。其中,fAMAE、fRMES和fMAE均小于0.2,R2均大于0.9。这表明,此代理模型具有显著性。图5是样本点真实值和预测值关系图,图中小圆点均匀地分布于理想直线的两侧,证明该模型具有较高的精度,可以用来拟合不同因子组合下的响应值。
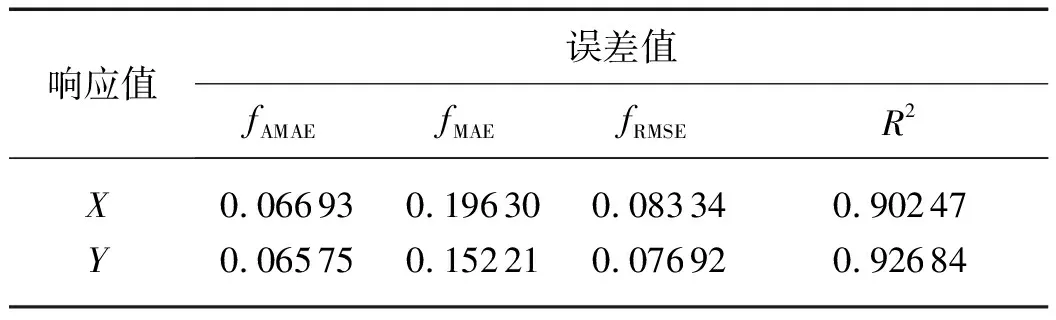
表3 评价指标
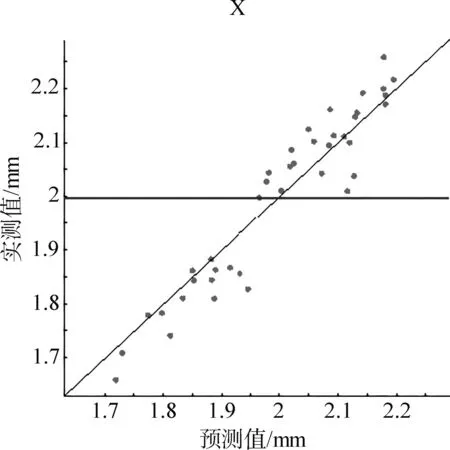
(a) 翘曲变形量
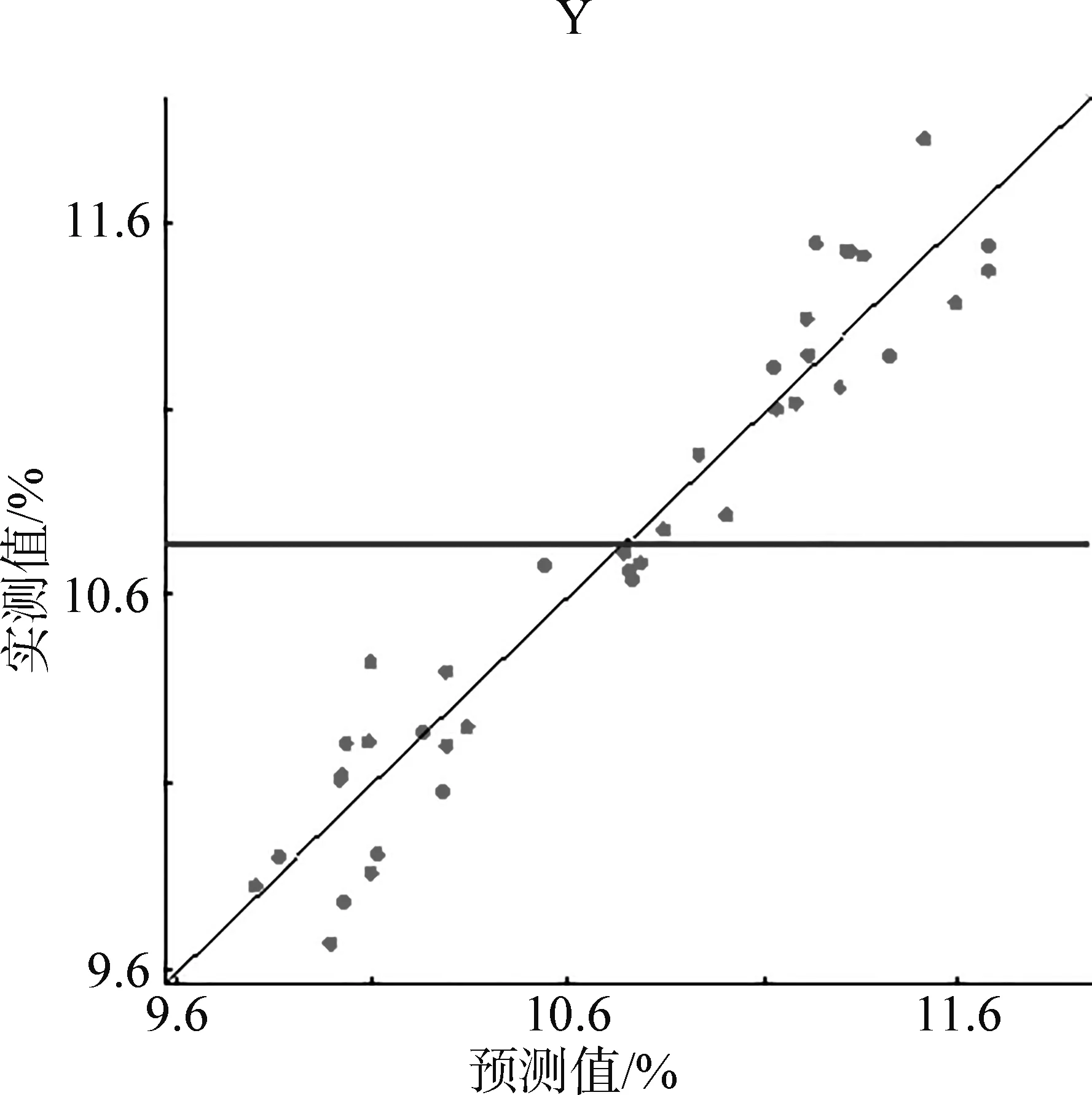
(b) 体积收缩率
2.3 基于NSGA-Ⅱ的工艺参数优化
遗传算法是仿照生物进化机制提出的一种用于优化工程问题的理论算法,采用迭代方法可以从新种群里寻求最优解或解集。为了快速寻求最佳注塑成型工艺参数及其对应的最佳响应值,减小人工调试成本。基于上节建立的Kriging模型,引入NSGA-Ⅱ算法寻求最优权衡解[8-9]。
使用Isight软件对响应值Y和Z进行优化,寻求与之对应的A,B,C,D,E工艺参数组合值,建立的目标函数及约束条件如式(1)。设置种群数量为12,进化代数为20,交叉概率为0.9,交叉分布指数为10,变异分配指数为20。
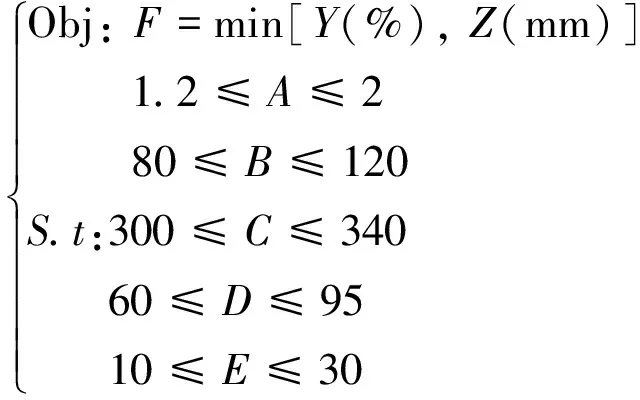
(1)
经过241次算法迭代,得到厚壁光导收缩和翘曲的Pareto前沿,迭代进化过程如图6所示。由图6可知,经过144次迭代,可得到最优解。翘曲变形量由之前的2.259 mm变为1.672 mm,比优化前降低了30%。体积收缩率由之前的11.827%变为9.653%,比优化前降低了18.4%。对应的工艺参数组合值分别为:熔体温度302℃、注射时间1.6 s、模具温度108℃、保压压力78%、保压时间为22 s。
3 试验验证
为了检验该多目标优化策略的可靠性,将得到的工艺参数输入到Moldflow中进行验证,结果如图7所示,其中翘曲变形量为1.665 mm,比多目标优化结果小0.42%。体积收缩率为9.641%,比多目标优化结果相小0.12%。经过优化后,产品翘曲变形量和体积收缩率得到了有效的控制,且模拟结果与多目标优化结果相比误差较小,均小于1%。将以上工艺参数组合用于实际生产,得到图8所示产品。分析产品外观,发现塑件表面光滑,色着均匀,未发现较大的收缩痕迹,无白点、气穴、流痕等注塑成型缺陷。证明基于Kriging和NSGA-Ⅱ的算法可以对厚壁光导产品的注塑成型工艺参数进行优化,该模型能有效节约试模和检验等生产过程的成本,提高生产效率。
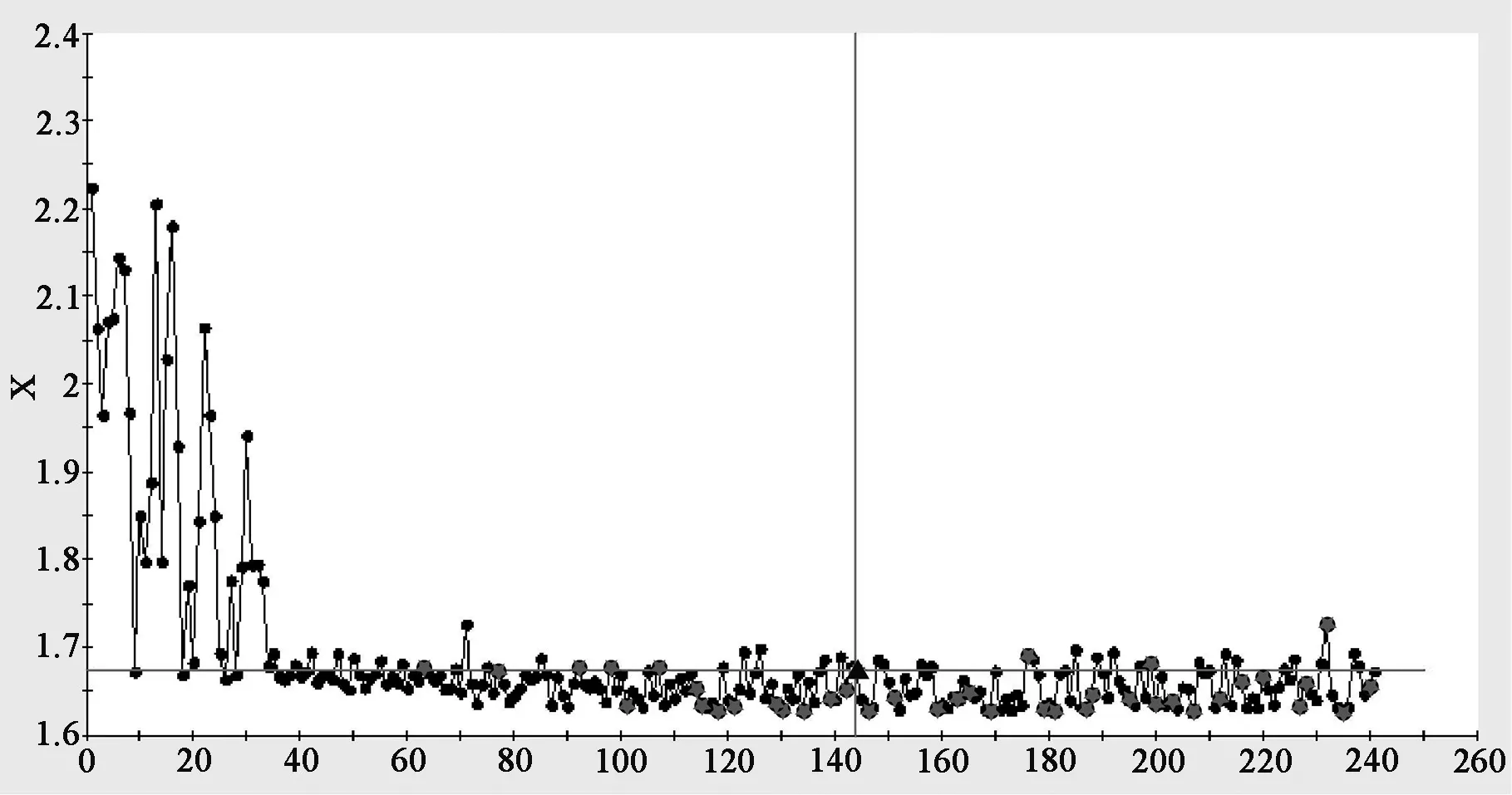
(a) 翘曲变形量进化过程
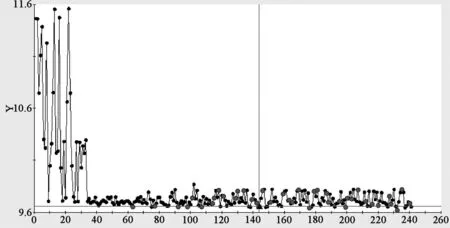
(b) 体积收缩率进化过程

(a) 翘曲变形量
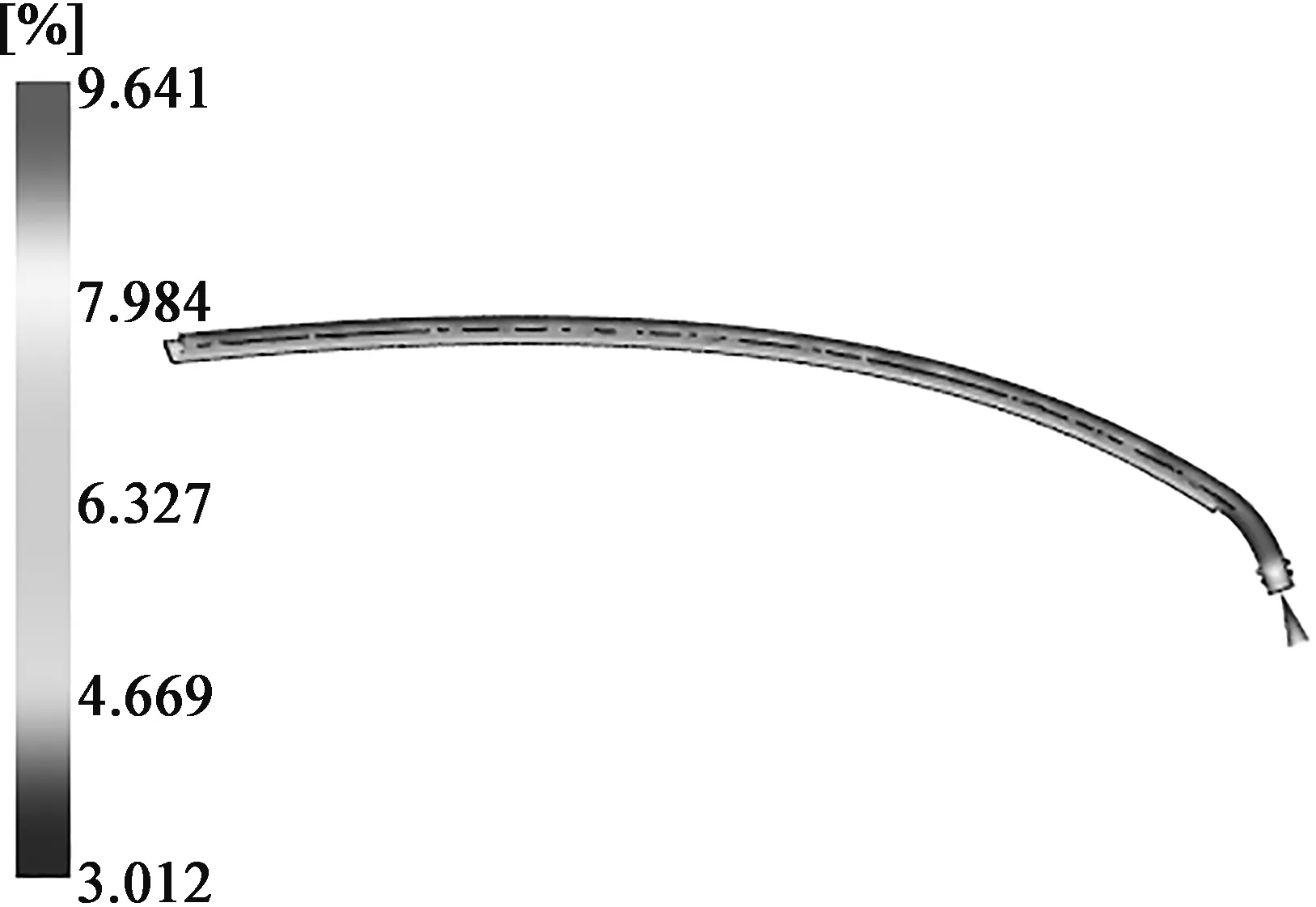
(b) 体积收缩率

图8 光导实物图
4 结 论
针对厚壁光导产品注塑成型过程中的体积收缩和翘曲变形等问题,采用基于Kriging模型与遗传算法结合的方式优化注塑工艺参数,结论如下。
1) 建立了可靠的Kriging代理模型。经过数理统计分析,关于翘曲变形量和体积收缩率的判定系数R2分别为0.902 47和0.926 84,均大于0.9,建立的模型具有较高的拟合精度,可用于代替因子和响应值之间的关系。
2) 基于NSGA-Ⅱ算法进行了翘曲变形量和体积收缩率的工艺参数寻优组合。利用NSGA-Ⅱ算法,对Kriging模型进行迭代进化,得到翘曲变形量为1.672 mm,体积收缩率为9.653%。各个因子分别为:A=1.6 s,B=108 ℃,C=302 ℃,D=78%,E=22 s。
3) 实现了基于Kriging模型和NAGA-Ⅱ算法对厚壁光导的翘曲变形和体积收缩的有效控制,通过试验验证,该方法能有效拟合注塑成型过程,可用于寻求最佳工艺参数组合。
