拉脱法测量液体表面张力系数实验中液膜变化的动态数值仿真

袁 颖，梁月林，陈俊志，李羽晴，张新峰

(广西中医药大学 a.药学院；b.基础医学院，广西 南宁 530200)

液体表面张力系数是表征液体本身性质的重要参量，精确测量液体表面张力系数在化工生产、船舶制造、水利学以及生物医学等领域具有重要意义. 目前，实验上测量液体表面张力系数主要方法有：拉脱法[1-3]、毛细管法[4]、最大泡压法[5]、悬滴法[6]、表面波激光干涉法[7]等，其中拉脱法使用较为广泛.

拉脱法测量液体表面张力系数实验中，在吊环拉出液膜的过程中，虽然可以观察到电压示数由小变大，到达峰值后又快速变小，直至液膜被拉断的现象，但液膜本身的细微变化过程肉眼不易观察. 为了更加直观地观测液膜变化过程，本文基于实验数据，对液膜变化的动态过程进行了二维和三维的仿真数值模拟.

1 实验数据采集

1.1 实验仪器

FD-NST-I 型液体表面张力系数测定仪(图1)、游标卡尺、蒸馏水、玻璃皿、录像设备.

1.2 实验过程录制

对硅压阻力敏传感器定标后，挂上实验用吊环，顺时针方向转动升降台大螺帽使液面上升，当环下沿全部浸入液体后，改为逆时针匀速转动该螺帽，这时液面下降，吊环下沿将拉出1层圆柱形液膜，此时利用2台录像设备同步录制液膜变化视频和电压变化视频.

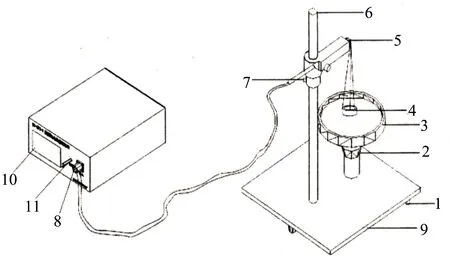
1．调节螺丝 2．升降螺丝 3．玻璃器皿 4．吊环 5．力敏传感器 6．支架 7. 固定螺丝 8．插头 9．底座 10．数字电压表 11．调零旋钮图1 FD-NST-I型液体表面张力系数测定仪

1.3 仿真数据提取

仿真数据提取中，如图2所示，设计了3个关键点：P1为环的左下端边缘，P2为h/2处液膜上的对应点，P3为液膜与水平面的交点.其中设置参量h为环底部离开水面的高度，d1为P2到环左壁边缘的水平距离，d2为P3到环左壁边缘的水平距离.

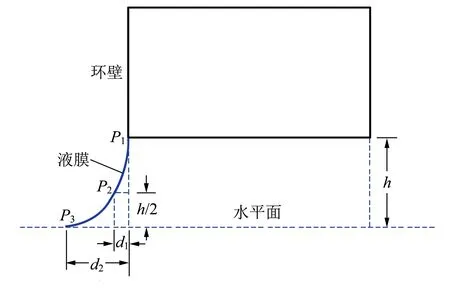
图2 液膜取值点的二维示意图

利用慢速播放器MPC对液膜变化视频每间隔1 s截图，Windows 10“画图”工具提取O，P1，P2，P3及M，N的像素级坐标.其中不动点O为测定仪升降台与其螺母的交点，以O为参照点,M和N为图中环的上下边缘中点，如图3 所示，依次获得图中的环高.

图3 液膜变化视频第20 s截图

为减小测量误差，采取多次采集关键点像素坐标，然后取其平均值进行数据分析和建模.

2 建立数值模型

2.1 建立回归分析数学模型

通过观察数据离散点图(图4～6)可知，U1,d1和d2都随h的变化而呈现出有规律的变化，因此，以h为自变量，分别以U1，d1，d2为依赖变量，做回归分析，根据散点图相近的变化趋势特点，统一建立数学模型：

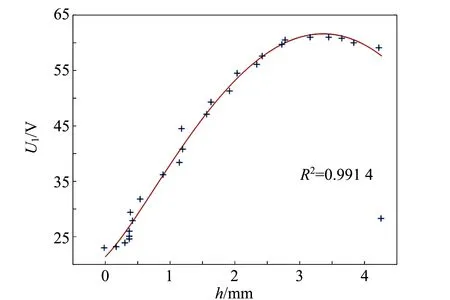
图4 U1与h的关系图

d1=β0+β1h+β2h2+β3h3+β4h4+lg (1+h)+eh.

(1)

经过回归分析模型逐步优化，从上述模型中筛除不显著因子，得到U1与h，d1和h，d2与h的非线性最小二乘回归分析数学模型：

U1=21.386 7+46.300 6h-5.706 4h2-

34.578 9 lg (1+h),

(2)

d1=-0.268 6+37.536h-13.777 2h2+3.363h3-

0.446 6h4-38.865 lg (1+h)+0.595 6eh,

(3)

d2=0.903 1+26.542 1h-7.711 3h2+1.423 3h3-

0.110 8h4-26.649 9 lg (1+h).

(4)

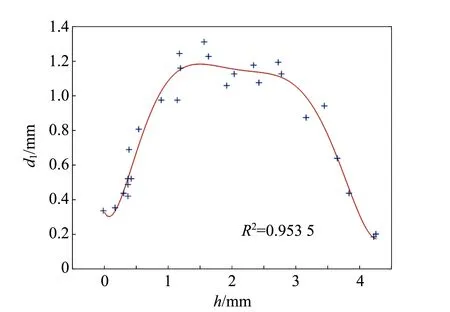
图5 d1与h的关系图

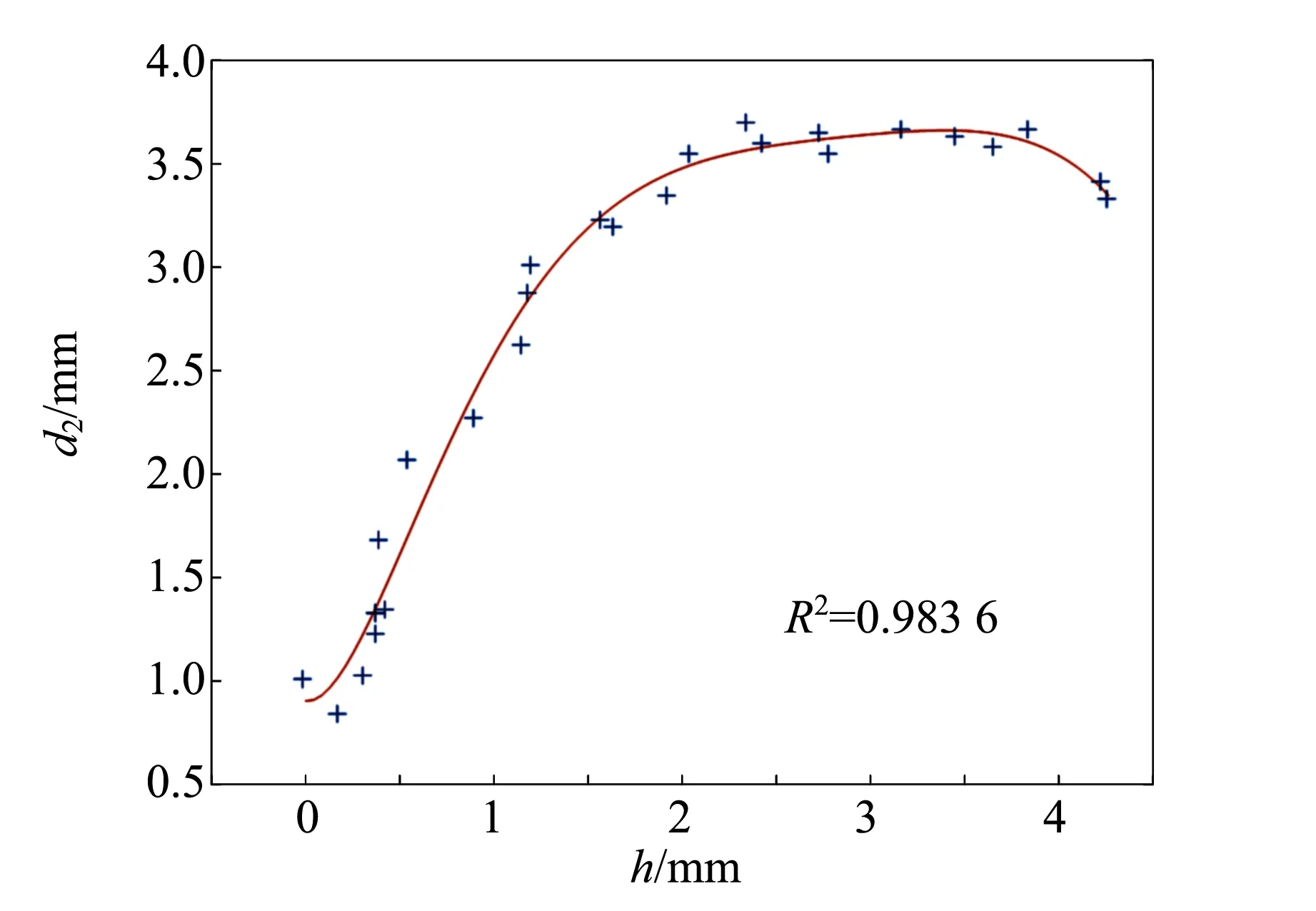
图6 d2与h的关系图

2.2 建立三次样条插值函数

所测数据中液膜断裂前h的最大值为4.254 8 mm，对h的取值区间[0，4.26]进行100等分，步长为0.042 6，可得101 个分点.当h=0+k×步长，k=1,2,…,101时，由已得的回归模型可得到对应的d1和d2的值.

利用每组的3个值h(k)，d1(k)和d2(k)，可求得P1，P2和P3的二维坐标，利用三次样条插值[8]，可得经过P1，P2和P3的三次样条插值函数的spline样条函数，此函数是1条光滑曲线，以此光滑拟合曲线近似表示液膜表面所在曲线.

3 动态可视化呈现

根据上述回归分析模型和三次样条插值拟合原理，为了直观描述实验过程，用Matlab 软件编写算法程序，并对整个液膜变化过程进行了二维和三维动态仿真.

3.1 二维动态仿真

根据吊环左右环壁的对称性，可以得到如图7～9所示的液体表面张力实验液膜二维变化的动态仿真过程(图中长方形为吊环的竖截面图).

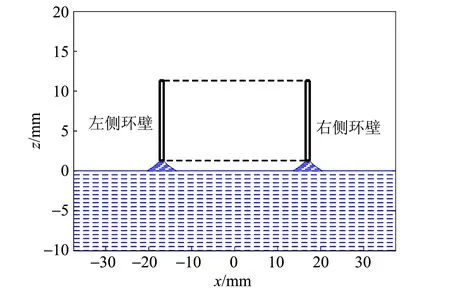
图7 初拉起液膜时的二维动态仿真截图

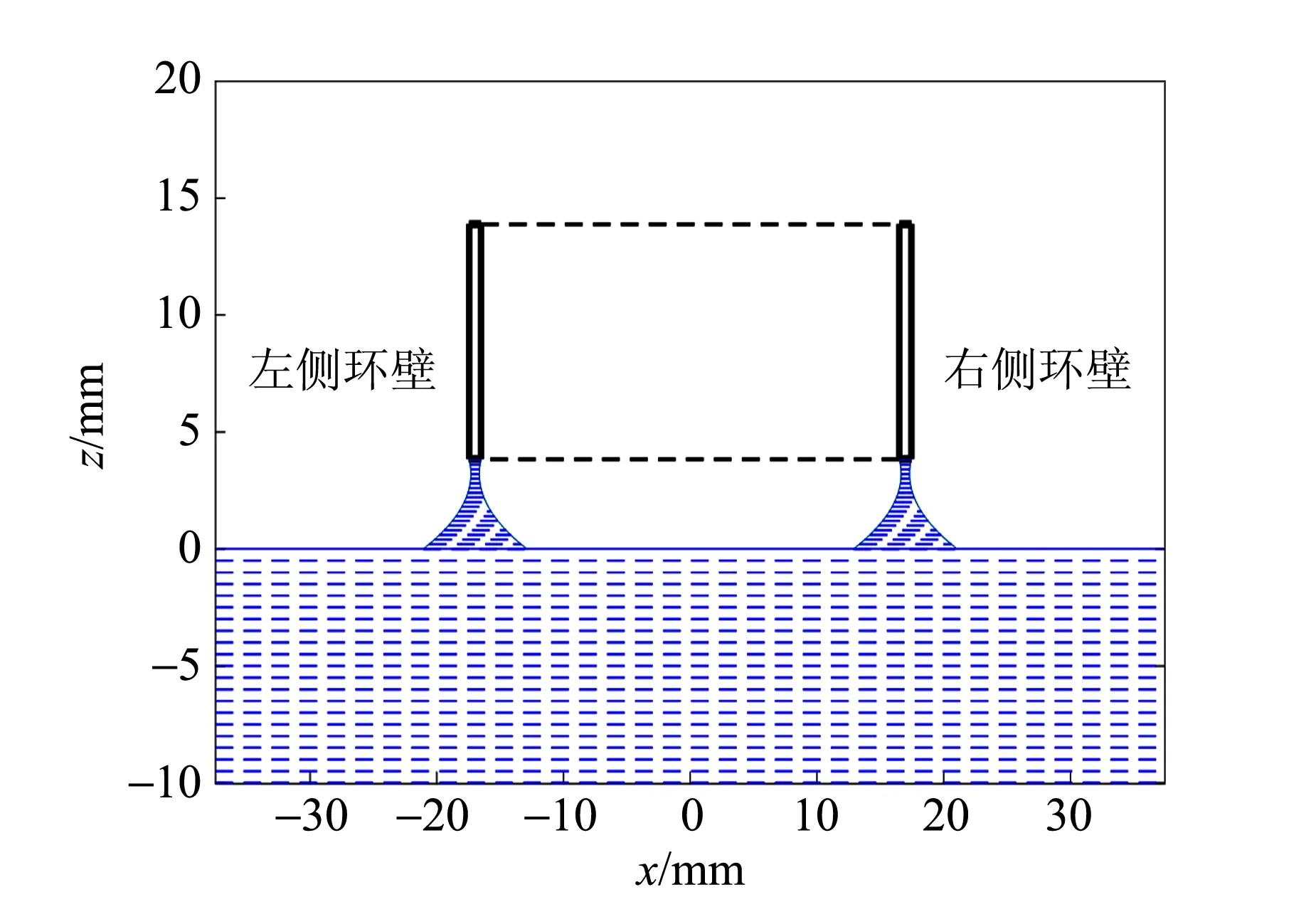
图8 电压值达到最大时液膜的二维动态仿真截图

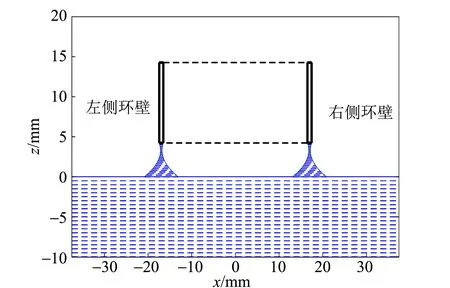
图9 液膜破裂前瞬间二维动态仿真截图

3.2 三维动态仿真

拟合以吊环竖直方向的中心线与水面的交点为极坐标的原点，把圆周角360°进行360等分，对每个h(k)，k=1,2,…,101，将前述所得三次样条插值拟合曲线上各点的二维坐标转换为极坐标，这些极坐标点绕吊环中心线每间隔1°旋转后，可得旋转后的三维极坐标. 依次类推，纵向得到不同旋转角度的光滑三次样条插值曲线，在水平方向以虚线连接每间隔相等角度的点，形成近似的水膜所在曲面，如图10～11所示.

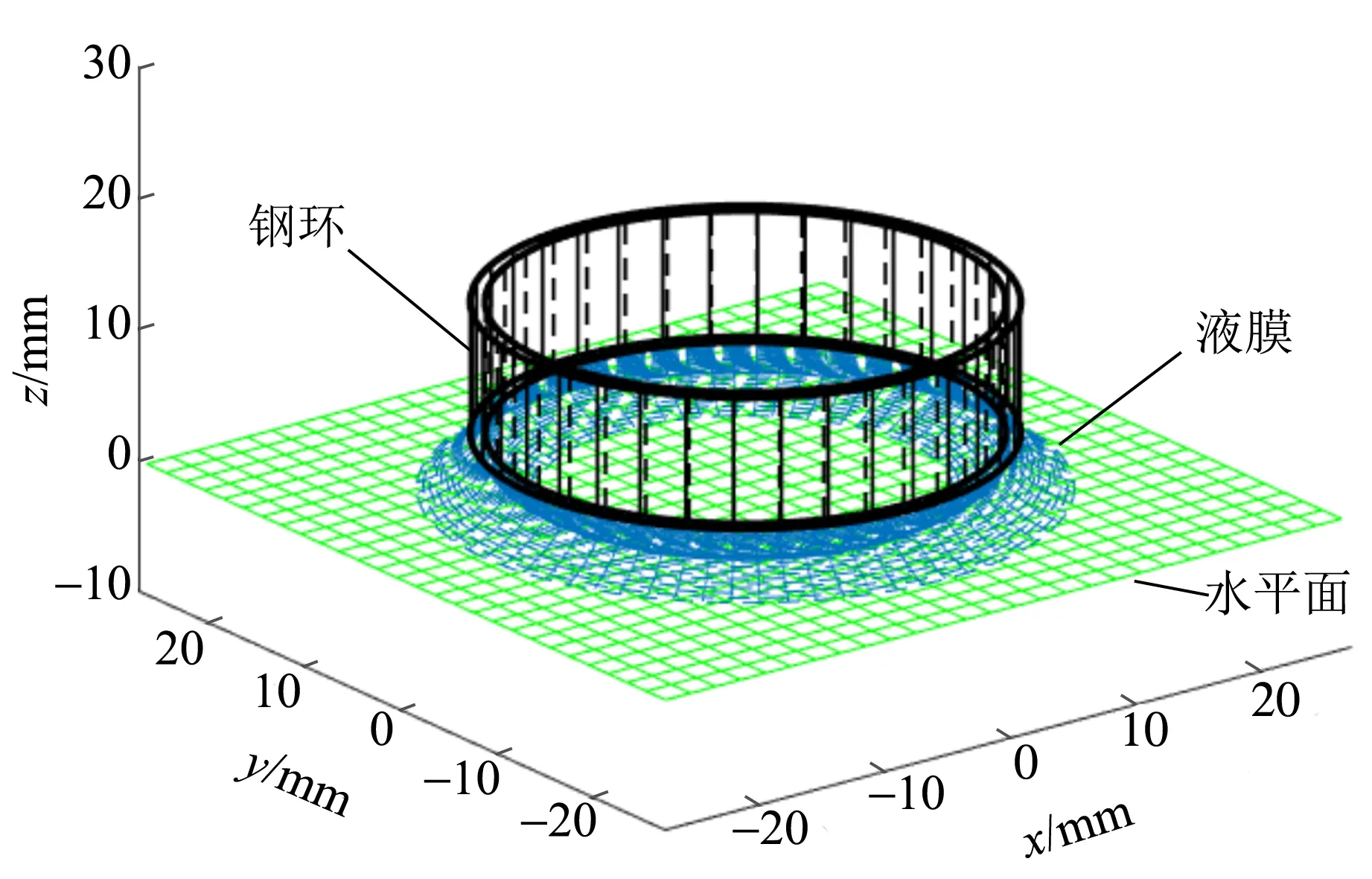
图10 液膜变化的三维仿真俯视图

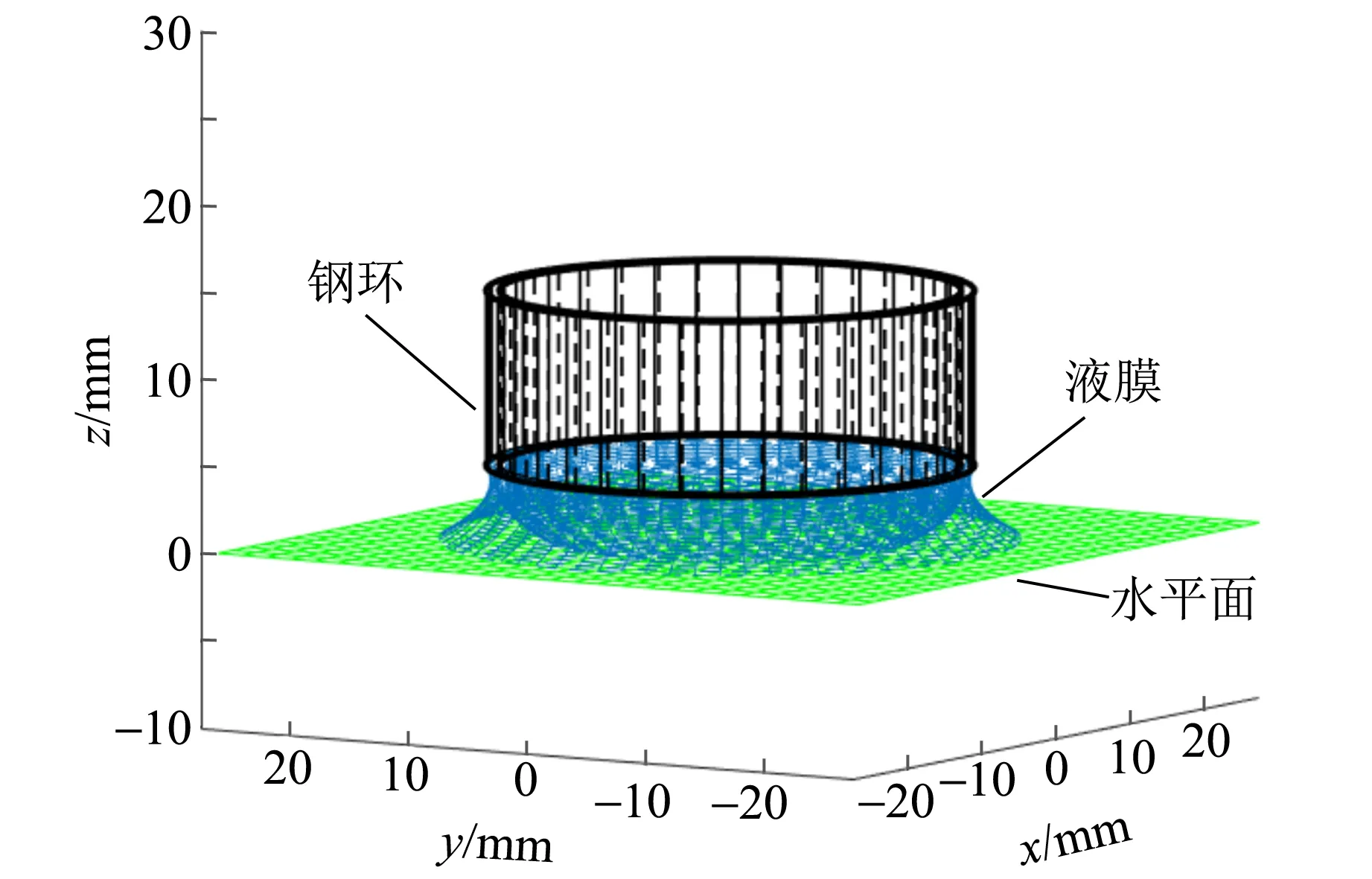
图11 液膜拉伸到最高位置的三维仿真平视图

二维动态和三维动态的仿真结果验证了实验中液膜所受到的表面张力先增后减的过程. 结果表明，数值仿真结果形象逼真地再现了液膜变化过程.

4 结束语

在液体表面张力系数测量实验中，对液膜的连续变化过程中3个关键点P1，P2和P3的坐标与吊环离开水面高度h的相互关系进行了精确的回归分析建模，并以此为基础利用三次样条插值法对液膜变化进行动态数值仿真. 二维和三维动态仿真的可视化呈现，可让学生直观观察拉脱吊环时液膜的变化过程，不仅激发了学生的学习热情，也让学生对液体表面张力及表面张力系数的相关概念理解更加深刻.