海上丝绸之路集装箱航线网络级联抗毁性研究

□ 王亚琨，薛宗杭

(大连海事大学 交通运输工程学院，辽宁 大连 116026)

随着21世纪海上丝绸之路战略的提出，构建高效海上集装箱航运网络极为迫切。但实际集装箱航运网络可能会受自然因素或突发事件等影响，致使港口或航线发生中断，失效港口的集装箱班轮只能挂靠邻接港口，若邻接港口货运量超过其自身所能容纳的最大容量，也会相继失效。因此研究港口失效时引发航运网络相继故障的过程，分析航运网络抗毁性具有重要意义。

目前相关研究大多侧重于负载-容量模型、负载重分配策略、节点失效方式。杨悦[1]研究了负载-容量线性及非线性模型，全局分配策略以及剩余容量差值分配策略四种情境下供应链网络级联失效过程。张金伟[2]通过设计基于节点属性的马尔科夫聚类算法(KL-MLC)来识别海上丝绸之路航运网络的社群结构，证明网络的鲁棒性受社群结构中的枢纽节点影响。曾庆成等[3]基于复杂网络理论方法，从平均距离、聚类系数、度及其分布等角度验证了海上丝绸之路航运网络是具有小世界效应和无标度特性的复杂网络。吕泽军[4]从失效方式、可调系数、负载重分配策略、增边策略等几个方面进行了网络抗毁性分析并从预防和补救两个方面提出了增强网络鲁棒性的措施。Fu Chao-qi等[5]从不同攻击策略研究网络的鲁棒性，采用多节点攻击策略分析了失效节点间的距离与网络失效规模之间的关系。吴迪[6]从港口和海上通道两个方面分析了航运网络中风险控制关键环节的形成因素及枢纽港的失效影响，针对海上丝绸之路集装箱海运的风险控制和安全保障提出了相应的对策及建议。刘丽娇[7]通过使用熵权法计算网络脆弱性量化指标来寻找集装箱航线网络中最脆弱的环节，针对脆弱性评价结果优化网络结构，对比分析网络优化前后的脆弱性变化。吴小欢等[8-9]根据航线网络设计参数OD流量和单位流成本的不确定性，定义了区间型情景集，建立了区间型绝对鲁棒优化模型，设计了将修正最短路算法与人工智能算法相结合进行求解的有效算法。

现有研究大都是基于复杂网络均匀负载开展的，对于动态负载下的网络级联研究较少。此外，在网络模型构建方面，负载-容量非线性关系是航运网络的核心特征之一，仅基于线性模型下的级联失效研究无疑简化了研究复杂度，考虑非线性模型下有向加权网络的研究具有重大意义。本文基于复杂网络理论，构建动态负载集装箱航线网络非线性模型，设立级联失效负载分配规则及抗毁性评价指标，运用主成分分析法识别网络关键节点，蓄意攻击关键节点或随机攻击网络节点，依据节点存活率及网络效率分析网络抗毁性，最后通过MATLAB实例仿真验证了模型的有效性。

1 海上丝绸之路网络模型的构建

集装箱班轮运输是按照固定的顺序依次挂靠在港口进行货物运输的，因此采用有向加权网络模型。如图1所示，为方便建模和求解，假设如下：

①网络中各节点只存在两种状态，即节点失效、节点正常运行，不存在节点的自我修复或者其他状态。

②当港口发生突发事件或集装箱作业量超过其最大容量时，判定港口处于失效状态，删除与之相连的边。

③边权重表示港口间的航线数量，当两个港口有多条集装箱航线经过时，边权重进行累加。如A-B-C-D，A-B-C-E-F,A-B-D-F,此时A-B边的权重为3，B-C边的权重为2，其余边权重为1。

基于上述假设，本文采用L空间拓扑模型，将集装箱航线网络描述为有向加权网络GW={V,E,W}。其中V={vn}表示港口集合，E={em}表示港口航线集合，W={wij}表示航线的权重集合，i,j=1,2,…，N。采用L空间拓扑模型构建集装箱航线网络，有利于对网络特性的研究以及网络关键节点的分析。

图1 边权重示意图

2 集装箱航线网络级联失效模型

2.1 航线网络级联失效规则

当节点vi发生失效后,其负载不会消失，而是分配给周边完好邻接点，有向网络负载转移规则如图2所示：当节点vi发生故障停止运作时，停止接收父节点j1、j2传输的负载，同时中断对子节点j3输出负载，节点vi上的负载将按照分配规则向父节点j1、j2返还，j3不再接收来自节点vi的负载。当被返还负载的节点j1、j2上的负载超出其自身容量时，会引发失效，从而促使负载再次分配，这样的过程循环下去，直至整个网络不再发生节点失效。

图2 级联失效过程图

2.2 加权航线网络级联失效模型

2.2.1 初始负载

(1)

(2)

式(1)为节点强度，等于与该节点相连的所有边的权值之和[10]，wij表示节点i与节点j的权重。式(2)为节点的初始负载，其中km表示节点m的度，α为可调系数，Γi为节点i的邻接点集合。

2.2.2 港口容量

以往研究表明负载-容量线性模型存在着一定的不足，于是本文采用更加符合实际的负载-容量非线性模型，表达式如下：

(3)

式(3)中，Ci为港口容量，β、γ为可调系数。

2.2.3 负载重分配策略

为有效降低失效过程中父节点继续失效的概率，采用节点剩余容量差值分配策略[1]。公式如下：

(4)

式(4)中，πj表示负载转移比例，Γi表示失效节点i的邻接点集合。

节点j上获得的额外负载：

(5)

2.3 动态负载加权航线网络级联失效模型

2.3.1 动态负载加权网络初始负载

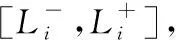
(6)

式(6)中，ΔL表示港口的动态负载变化量，η、δ为动态可调系数，η∈[-1,1]，δ∈[0,1]。

式(7)表示t时刻港口上实时负载：

(7)

2.3.2 动态负载加权网络负载重分配策略

根据上文，定义负载重分配公式如下：

(8)

节点j上获得的额外负载：

(9)

式(8)中，πj表示负载转移比例，Γi表示失效节点i的邻接点集合。

2.4 模型算法及网络评价指标

2.4.1 模型算法

Step0：根据邻接矩阵构建海上丝绸之路航运网络。

Step1：计算网络特征指标。采用主成分分析法进行节点综合重要度排序。

Step3：初始时刻，对网络上节点分别进行随机攻击或按重要度排序蓄意攻击。

Step4：获取失效港口邻接港口集合Γi，进行失效港口负载重分配。

Step5：移除失效节点及失效节点与其邻接点的连边。

Step6：转移失效港口负载，判断邻接港口是否发生级联失效，若发生失效，将港口划归到失效港口集合，更新网络剩余节点负载，然后返回Step4进行负载重分配，否则进入Step7。

Step7：若网络中没有港口发生失效，结束级联失效过程。

Step8：统计失效节点数量，计算网络抗毁性指标。

2.4.2 网络抗毁性指标

①节点保留率G:未失效节点数占网络中港口总数比例。节点存活率反映了航运网络中港口失效后的最大连通性，计算公式如下：

(10)

式(10)中，N′为未失效节点数，N为节点总数。

②网络全局效率：网络中各节点对最短路径的倒数均值。网络效率反应网络连通性，网络发生级联失效后，网络效率越高，则表示网络抗毁性越强。

(11)

式(11)中，dij表示i点到j点的最短路径，当i点与j点无连边时，记dij=∞。

③网络阈值βc、γc:在海上丝绸之路航运网络模型中，网络节点容量与β和γ有关，节点容量越大，网络越难触发级联失效，反之，节点容量越小，网络上任意节点的轻微扰动就越容易触发级联失效。但容量系数β、γ与网络建设成本呈正相关性，因此采用网络阈值βc、γc作为网络抗毁性度量指标。

3 网络关键节点识别

海上丝绸之路航线网络是具有小世界特性及无标度特性的复杂网络，网络中存在一些关键枢纽节点，本文从度中心性、特征向量中心性、介数中心性、接近度中心性、Page-rank以及节点入度等六个方面综合分析网络节点重要度。

(12)

(13)

(14)

(15)

(16)

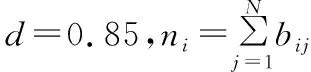
运用SPSS软件进行因子分析，然后进行KMO和Bartlett检验，表1显示，KMO值为0.841，近似卡方值为1083.852，自由度df为15，显著性水平为0，说明效度评定好，适合做因子分析。

表1 KMO和巴特利特检验

各指标成分得分系数由表2和表3计算得出，将系数代入后得出港口综合排名表达式为(17)-(19)：

y1=0.444c1+0.366c2+0.365c3+0.395c4+0.431c5+0.44c6

(17)

y2=-0.075c1-0.671c2+0.496c3+0.484c4-0.247c5+0.032c6

(18)

y=0.8303y1+0.1035y2

(19)

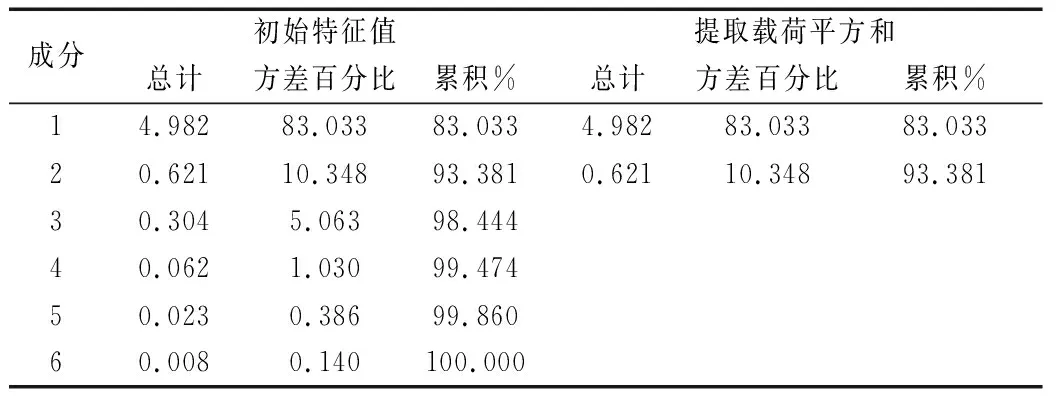
表2 主成分分析结果

表3 成分矩阵

4 实例计算分析

4.1 数据来源及处理

根据2021年马士基、中远、长荣等全球十大航运公司官网提供的航线相关数据进行实例计算，选取部分航线，运用pajek软件绘制集装箱航运网络，如图3所示，港口数n=99，航线m=279，航线权重w=444。

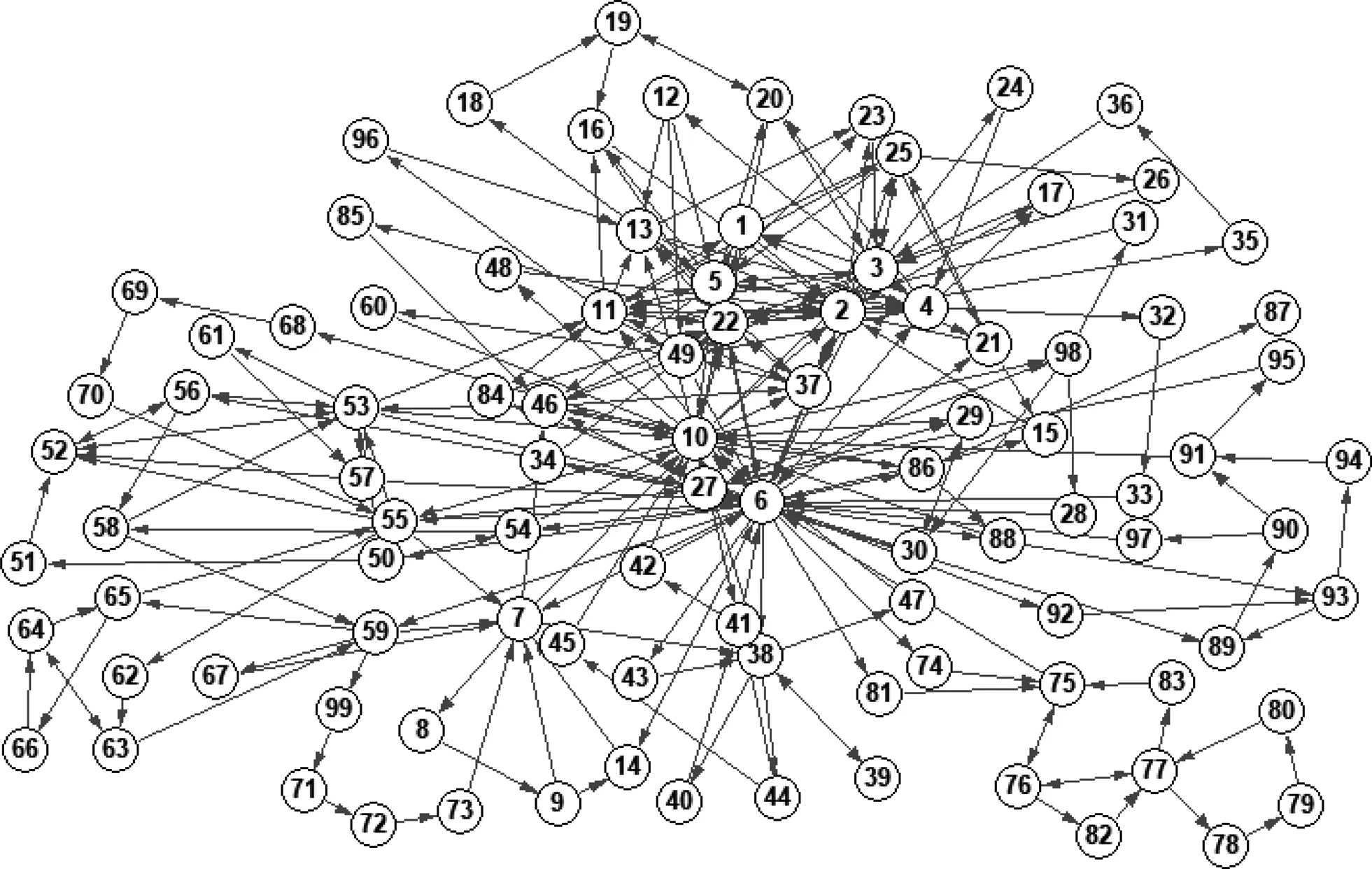
图3 集装箱航线网络图

通过网络的拓扑邻接矩阵计算网络的度、初始负载和节点容量(部分节点)，如表4所示。

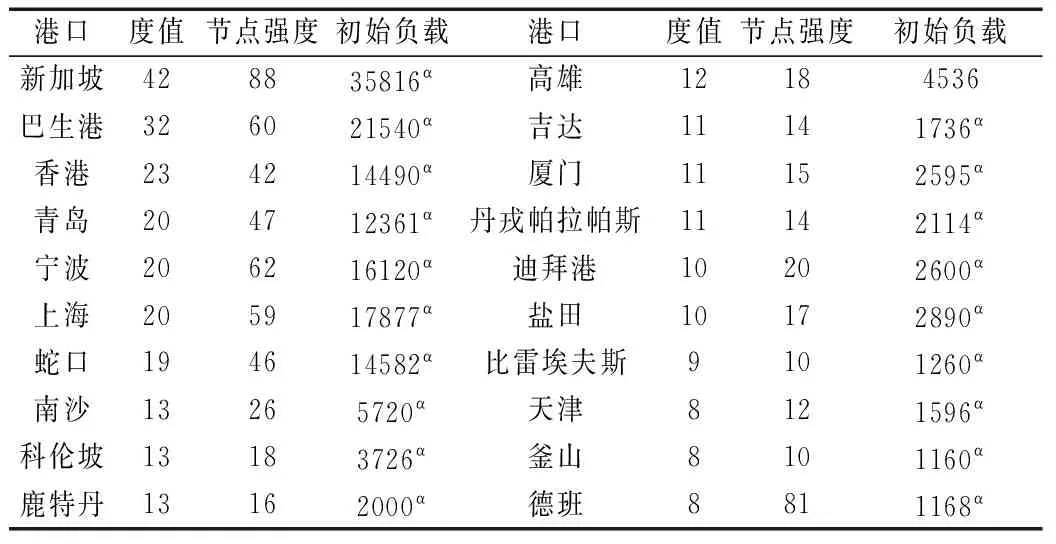
表4 港口节点数据表

标准化处理港口中心性特征指标数据，根据主成分分析法得出港口综合排名，排名前10港口见表5，新加坡港除了特征向量中心性外，其余指标均位列第一。在整个航运网络中，新加坡港居于首位。

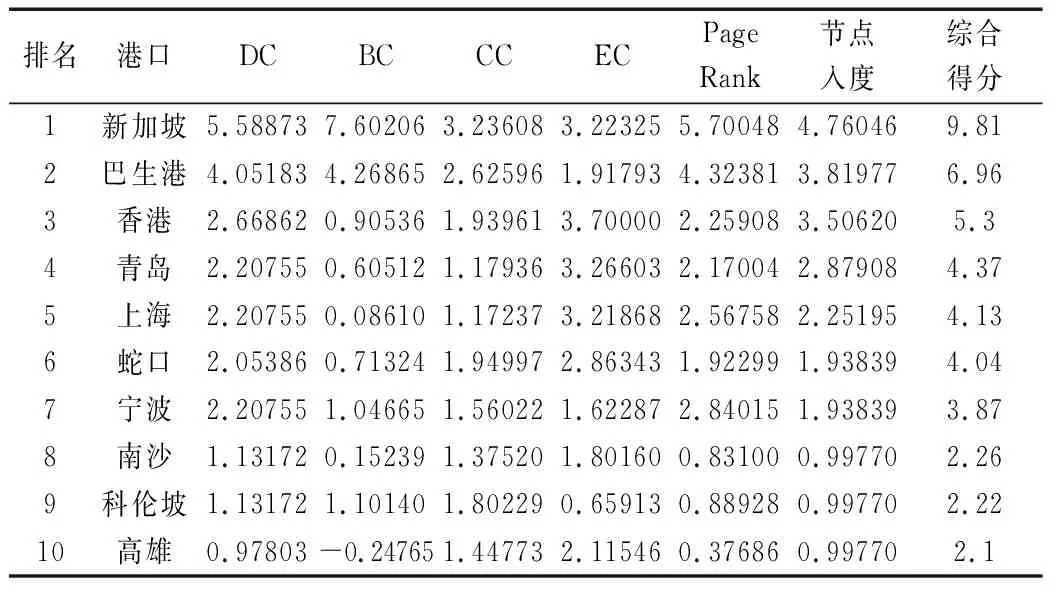
表5 港口节点综合得分表

4.2 网络抗毁性评估

4.2.1 节点保留率分析

对网络中的港口进行随机攻击，研究α与β(γ取0.5)及α与γ(β取1.3 )对海上丝绸之路集装箱航线网络级联失效抗毁性的影响。为保证数据的合理性，相同系数下，进行2000次随机攻击模拟，取均值作为最终结果，见图4，结果表明α值越小，β阈值越小，相同β下，α值越大，网络节点存活率越低，网络抵御风险能力随着β值的增大而增强。

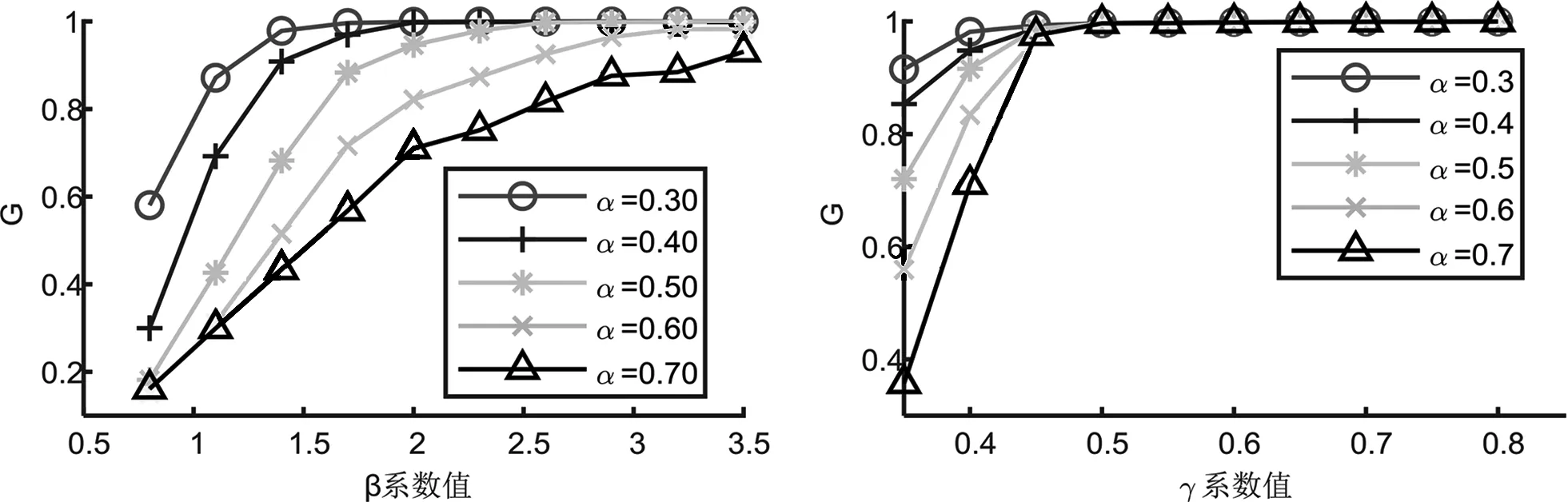
图4 节点保留率分析

4.2.2 综合重要度蓄意攻击

按照节点综合重要度次序进行蓄意攻击，考虑到多点同时失效的可能性较小，本文假定初始失效节点数为1，研究不同容量系数对于海上丝绸之路集装箱网络的抗毁性的影响。

蓄意攻击综合重要度前五的港口，见图5，β=0.15时，网络抗毁性较差，任一节点失效都将导致网络大面积崩溃。节点存活率随迭代次数的增加而降低，攻击新加坡港时，网络在迭代11次后存活率降为0，攻击其余港口时，网络在11次迭代后相继全部失效；β=0.3时，攻击新加坡港和巴生港节点发生了级联失效，攻击新加坡港时，网络整体存活率在11次迭代后为0，攻击巴生港网络在13次迭代后达到稳定，节点存活率为0.04，这表明随着β系数的增加，节点的存活率提高，网络的抗毁性增强；β=0.45时，仅有攻击新加坡港造成网络级联失效；β=0.48时，攻击任意节点网络均未发生级联失效，网络达到稳定状态，网络抗毁能力强。

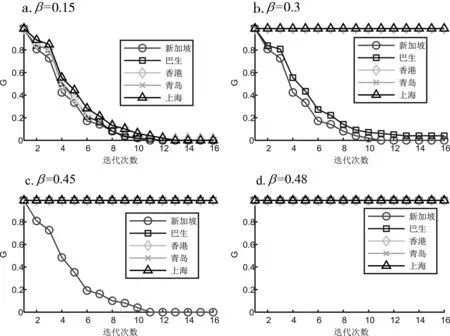
图5 级联失效过程迭代

结合四图发现，节点综合重要度越高，其失效对网络造成的影响越大，网络越容易发生崩溃。网络的抗毁性随着β值的增大而增强，β值越大，网络级联失效造成的影响越小，当网络容量达到某一定值时，网络抗毁性不再受β值的变化影响。

4.2.3 网络阈值分析

为分析容量参数β、γ对海上丝绸之路网络抗毁性和节点存活率的影响，本文通过蓄意攻击综合重要度排名第一的节点，分析在不同负载参数下的网络容量阈值。

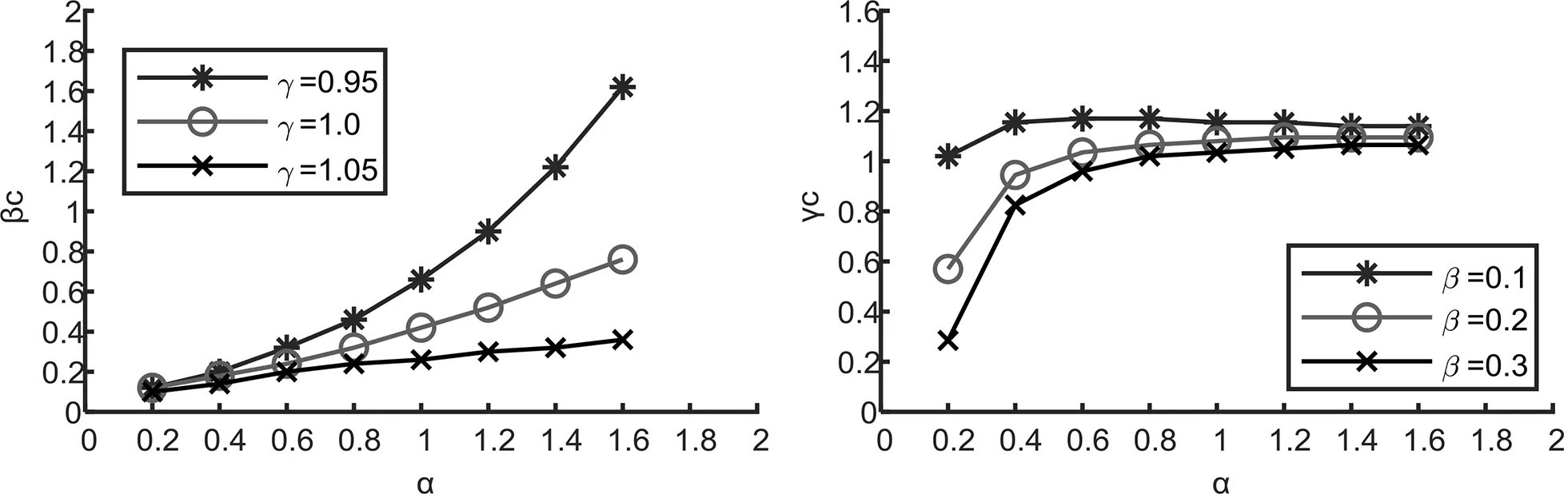
图6 网络阈值分析

由图6可知,相同α下，网络的抗毁性随β、γ值的增大而增强，β值与γ值呈负相关性，即βc值随着γ值的增大而减小。β阈值和γ阈值随着α值的增大而增大，且不同的α值对应的βc以及γc差异也较大。随着α值的不断增加，网络的抗毁能力不断下降，网络鲁棒性变差。

4.2.4 网络效率分析

为分析容量参数对网络效率E的影响，随机攻击港口及蓄意攻击综合重要度第一港口，分析两种攻击方式下β、γ与E的变化规律，结果如图7所示。

图7 网络效率分析

分析图7a和图7b，相同β或γ下，容量系数α越大，网络效率E越小，网络的抗毁能力越差，网络效率E随着容量参数的增加而提高，网络的鲁棒性增强。容量系数α越小，网络达到稳定时对应的容量阈值β、γ越小。

对比分析蓄意攻击以及随机攻击，发现随机攻击网络效率E远大于蓄意攻击，这表明随机攻击具有鲁棒性，网络容错率高，蓄意攻击方式下网络十分脆弱，网络关键节点是影响网络效率的重要因素。

4.3 动态负载下抗毁性评估

本文以非动态负载下初始负载值为基数，通过收集港口近五年的集装箱吞吐量和增长幅度预测负载量的浮动范围，见表6，增幅最大为12.9%，降幅最大为9%，即[Li(1-9%),Li(1+13%)]，随机生成500种情景，设置α=0.8，β=0.3，γ=0.95。采用绝对鲁棒优化模型求解，500种情境下的容量参数分布如图8、图9所示。

表6 近五年港口集装箱吞吐量

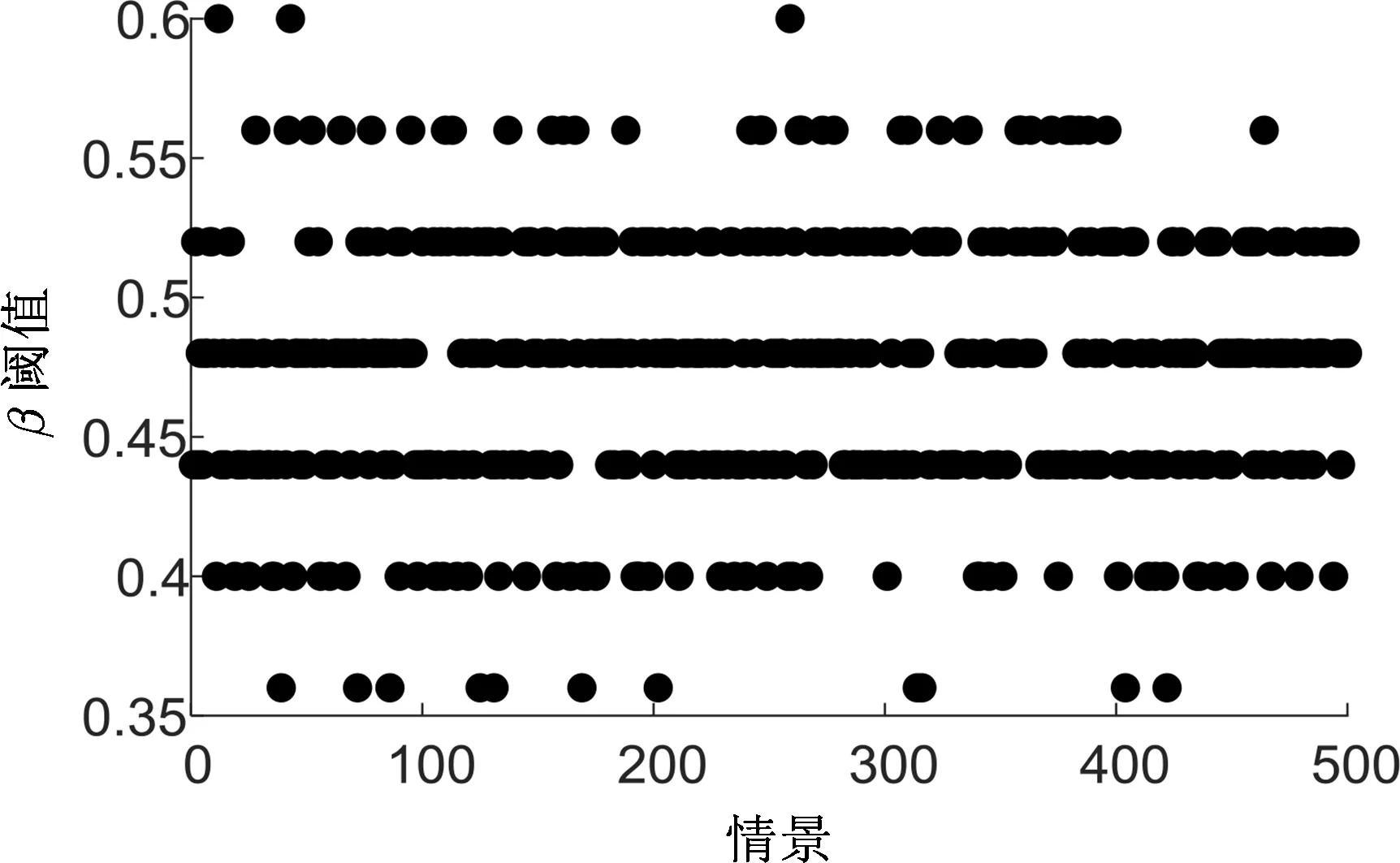
图8 动态负载下β阈值分析

图9 动态负载下γ阈值分析

如图8和9，动态负载下阈值βc集中分布在0.44～0.52，少数βc低于0.4或高于0.56，非动态负载下，阈值Pc≈0.48。网络阈值γc集中分布在1～1.03，少数情景下阈值低于0.98，非动态负载下，网络阈值γc≈1。采用绝对鲁棒优化，悲观准则下阈值βc=0.6,γc=1.03，乐观准则下βc=0.36,γc=0.96，结合实际情况，疫情过后，全球海运市场总体呈向好趋势，港口集装箱吞吐量将保持低速增长，从鲁棒性角度出发，为保障航运网络高效运作，避免失效造成巨大经济损失，选择悲观准则下的网络阈值更合适。

5 结语

本文基于有向加权集装箱网络，建立了动态负载下容量负载非线性模型，然后以海上丝绸之路集装箱航线网络进行实验仿真，从网络关键节点、负载容量可调、不同攻击方式、网络效率等角度，对整个网络的抗毁性进行研究分析。结果表明节点重要度越高，对网络的抗毁性影响越大。随机攻击优于蓄意攻击，可增强网络的容错率。节点的初始负载以及容量是网络抗毁性的重要影响因素，提高节点容量可以减小邻接点分担负载过程中的失效率，提高网络的抗毁能力。下一步将考虑实际网络中邻接港口距离的差异性，设置新的负载重分配规则，进一步研究集装箱航运网络的抗毁性。