桥梁检测中多尺度有限元模型的应用

刘炎，李从财

（江西省交通运输科学研究院有限公司，江西南昌 330200）

0 引言

根据对桥梁结构破坏情况的分析，结构破坏程度最为严重的区域通常出现在柱端、梁端及下层节点等处。当前常用的SAP2000、PKPM、ETABS 等桥梁结构设计分析软件通常应用杆单元和板壳单元等进行宏观模型构建与分析，这种处理技术计算量小，但是无法反映桥梁结构破坏发生的微观机理。此外，研究人员还偏向于使用ANSYS、MSC、ABAQUS 等大型有限元软件构建实体单元较为复杂桥梁结构的微观模型，虽然有利于更好地把握桥梁结构局部性破坏过程，但计算量极大，收敛性也较差[1]。如果将局部构件从整体桥梁结构中取出后展开实体模型分析，则很难进行其边界条件和受力过程的模拟。结合实践经验来看，桥梁结构破坏过程是宏观层面和微观层面的混合，破坏往往在某些部位较为严重，而在其余部位则较小，故采用以上两种结构处理方法均难以满足工程需要，必须寻求一种折中的结构分析技术，因此多尺度有限元模型是较好的选择。

20 世纪80 年代E·C·汉勃利在结构荷载横线分布计算过程中提出梁格法理论，并进行了应用分析，这种方法在计算机技术并不发达的年代主要借助梁单元进行整体式梁应力横向分布的手工计算。《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）提出了适用于桥梁结构精细化分析的空间梁格分析模型、折面梁格分析模型及考虑薄壁墩效应的自由度单梁模型等简化模型，能有效弥补单梁分析模型中空间效应缺失的弊端。但以上两种处理方式均针对梁单元建模，均为桥梁结构简化分析模型，对于精度较高的情况，必须将梁格划分得更为细致，费时费力，且结果精度无法保证。应用多尺度分析模型，能降低建模和计算成本，提高计算精度，还能较好地进行桥梁结构精细化分析。结合梁单元分析假设，梁高跨比在10∶1 以下时，计算中剪切变形影响便可忽略不计。大跨桥梁基本满足这一条件，所以采用宏观模型进行桥梁结构整体力学特性分析切实可行，但进行桥梁检测时必须进行局部应力测试[2]。

基于以上原理，本文采用Midas Civil 有限元软件尝试进行桥梁结构多尺度计算，通过构建不同尺度单元耦合方程，进行整体框架模型及框架复杂节点多尺度模型分析，并通过比较分析实测值和理论值，研究多尺度有限元模型在桥梁检测中应用的可行性。

1 多尺度有限元模型

多尺度有限元模型由不同尺度的模型构成，主要通过不同单元及算法进行结构分析，通过选择合适的连接方式进行宏观尺度模型和微观尺度模型协同设计，以便更好地把握结构性能。

1.1 模型节点耦合

多尺度模型建模过程中涉及不同有限单元及不同的节点自由度，在多尺度有限元模型构建过程中很难确保不同界面单元准确连接。若不同种类单元具有相同自由度时，只需进行共节点耦合，而若不同种类单元具有不同自由度，则必须建立约束方程。板壳单元、实体单元和梁单元在宏观模型和精细化模型间可分别通过三种方式从低维度单元向高纬度单元过渡：板壳单元向三维实体单元过渡主要由线过渡为面；梁单元向三维实体单元过渡主要由点过渡为面；梁单元向板壳单元过渡主要由点过渡为线。进行混凝土桥梁检测过程中，空间梁单元和三维实体单元共节点时主要采用铰接方式，这显然不符合实际。人工编写约束方程的过渡方式十分繁琐，为此，本文主要采用刚性区自动构建约束方程，以确保多尺度模型单元界面位移的协调性。

1.2 矩形截面简支梁多尺度模型

为进行刚性区自动构建的约束方程在三维实体单元和空间梁单元混合模型中正确性和有效性的分析，必须构建矩形截面简支梁进行计算。根据《公路桥梁荷载试验规程》（JTG/T J21—01—2015），简支梁控制截面是正弯矩最大的跨中截面，为此，应在模型跨中长度分别取0、0.1L、0.2 L、0.3 L、0.4 L、0.5 L、0.6 L、0.7 L、0.8 L、0.9 L、1.0 L 的情况下建模（其中L 为简支梁跨度），并比较分析跨中截面应力和变形。矩形截面长200mm，宽150mm，梁跨度为3 000mm，建模材料的弹性模量为3.54×104MPa，材料容重25.5kN/m³，均布荷载及集中荷载分别为1.15kN/m 和10.4kN/m。构建起的多尺度模型中，底层梁柱端为实体单元，其设计长度为梁柱横截面长度的1.5倍，上部构建均采用梁单元，并建立梁单元-实体单元界面耦合约束方程。混凝土单轴应力应变关系上升段采用《混凝土结构设计规范》（GB 50010—2010）所给出的公式，而下降段主要采用双线性等向强化模型，假定钢筋屈服后的弹性模量取0。

分析均布荷载和集中荷载作用下模型结构响应程度，所得到的结果具体见表1，由表中计算结果可知，多尺度有限元模型三维实体单元模型、整体杆系单元模型结果的吻合程度非常高，特别是计算检测过程中控制试验荷载的加载效率时所涉及的截面内力，取值非常接近甚至一致。当跨中区段局部模型长度增大时，因受到均布荷载的作用，跨中挠度取值稳定，而集中荷载作用下跨中挠度则随区段长度的增大而增大，最大最小值之差为0.41%。均布荷载和集中荷载下多尺度模型及整体杆件模型跨中挠度差值最大分别为0.34%和0.62%；均布荷载和集中荷载下跨中截面下缘正应力和整体杆系模型之差最大分别为0.54%和2.21%。由此可见，通过刚性区自动构建约束方程的方式建立多尺度有限元分析模型的处理方式切实可行。

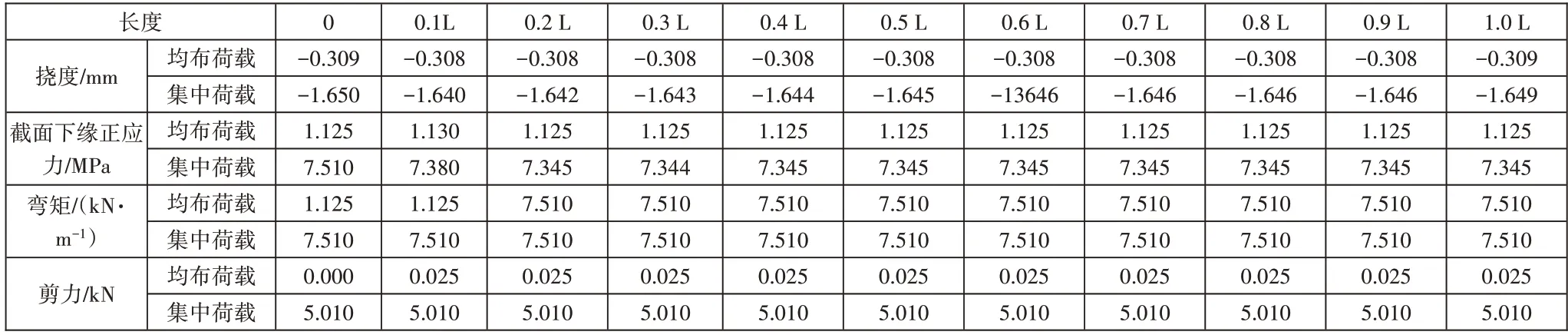
表1 均布荷载和集中荷载作用下结构响应程度

2 工程实例

某等截面三跨预应力混凝土连续箱梁桥跨为28m+35m+28m，直腹板单箱双室截面形式，截面高2.0m，顶底板宽9.2m 和5.4m。桥面横向设计宽度9m+2×0.5m，公路-Ⅱ级设计荷载，箱梁采用C50混凝土材料。

2.1 有限元模型构建

采用Midas Civil 软件建立该桥梁结构多尺度有限元模型，结合桥梁对称性结构特征以及《公路桥梁荷载试验规程》（JTG/TJ1—01—2015），以墩顶截面与中跨跨中截面为试控制断面。考虑到该桥梁结构实际，其有限元模型通过三维实体单元模拟，Midas Civil 软件中并未提供实体单元中预应力实现的具体方法，本文所构建的模型中主要采用以下方法实现实体单元预应力：结合设计图纸，在预应力钢筋实际布置位置分割实体单元，并将分割后的实体单元预应力钢筋位置处节点连接后建立梁单元，通过梁单元降温方式施加预应力，以进行实体单元预应力的模拟。

在建模过程中，墩顶位置处分别取支点左右2.0m的腹板与顶板变化区段，中跨跨中位置处则取中跨跨度0.2 倍进行细化性建模。通过刚性区法连接三维实体单元和梁单元，构建约束方程，确保节点变形过程的协调性。该等截面三跨预应力混凝土连续箱梁有限元模型总节点数为74 325，实体单元数为58 965，梁单元数为720。所构建的有限元模型见图1。结合分析目的，以中跨跨中及墩顶截面为测试截面，并在试验车辆偏载侧腹板外侧沿梁截面高度均匀布置应变测点。此外，在翼缘板处布置一个测点，将所设置的12 个应变测点依次标号为Y-1～Y-12。考虑到墩顶截面挠度无变化，故仅在跨中截面设置编号依次为N-1、N-2、N-3 的三个挠度测点，并沿着跨中截面底板宽度向均布。

图1 等截面三跨预应力混凝土连续箱梁有限元模型

2.2 静载测点布置及结果分析

静载测点的布置必须综合考虑等截面三跨预应力混凝土连续箱梁各主要构件控制截面及控制点在试验荷载下的可能受力状态，确保能够得到真实合理的结构强度及刚度实测结果。

根据桥梁结构在设计车道荷载下最不利受力状态，考虑桥梁承载力要求的基础上选取荷载试验工况。根据试验环境、试验目的、设计加载量等进行加载车辆选择，并保证符合静力试验荷载效率方面的要求。加载位置确定时必须选择最少的加载车辆取得最大的荷载效果，并满足试验所要求的测试项目测读需要。为节省试验时间，应在能够达到试验目的的基础上尽可能减少加载位置。本试验主要选用重载汽车或施工机械设备，所拟定的加载方案如下：

工况一：第二孔跨中正弯矩加载方案，即通过两辆解放车进行三级荷载加载，分别为0 载→一级荷载（305.5kN）→0 载，0 载→二级荷载（585.5kN）→0 载，0载→三级荷载（810.5kN）→0载。

工况二：1#墩负弯矩加载方案，即通过4辆解放车进行三级荷载加载，分别为0 载→一级荷载（605.5kN）→0 载，0 载→二级荷载（1 005.5kN）→0 载，0 载→三级荷载（1 510.5kN）→0载。

应用本文所提出的多尺度有限元模型进行荷载计算，结果见表2～表4。表中正数表示挠度向下，负数表示挠度向上。由表2可知，在工况一荷载形式下，一级加载、二级加载及三级加载试验下该桥梁跨中截面测点挠度校验系数取值分别在0.72～0.85、0.75～0.89及0.70～0.85，相关规范所规定的预应力混凝土桥梁挠度校验系数取值范围为0.70～1.00，故测点挠度校验系数取值符合规范要求，且取值分布较为均匀，不存在畸高和畸低等突变现象，表明该桥梁竖向刚度较大。

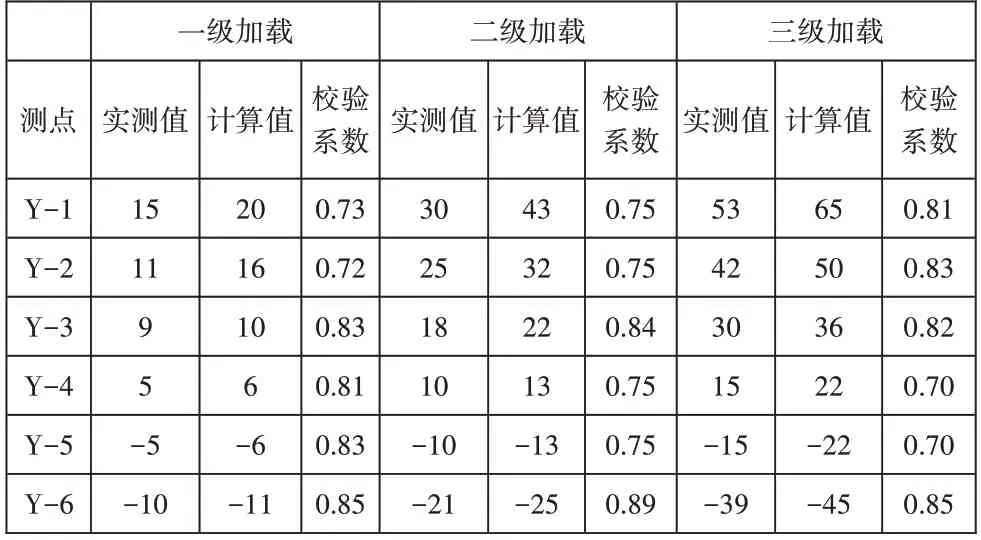
表2 工况一跨中截面应变试验结果 单位：με

由表3可知，在工况二荷载作用下，一级加载、二级加载及三级加载试验下该桥梁墩顶截面测点挠度校验系数取值分别在0.65～0.85、0.77～0.87 及0.81～0.88 之间，相关规范所规定的预应力混凝土桥梁挠度校验系数取值范围为0.70～1.00，故该桥梁墩顶主要测点挠度校验系数取值均满足规范要求，桥梁竖向刚度足够大。

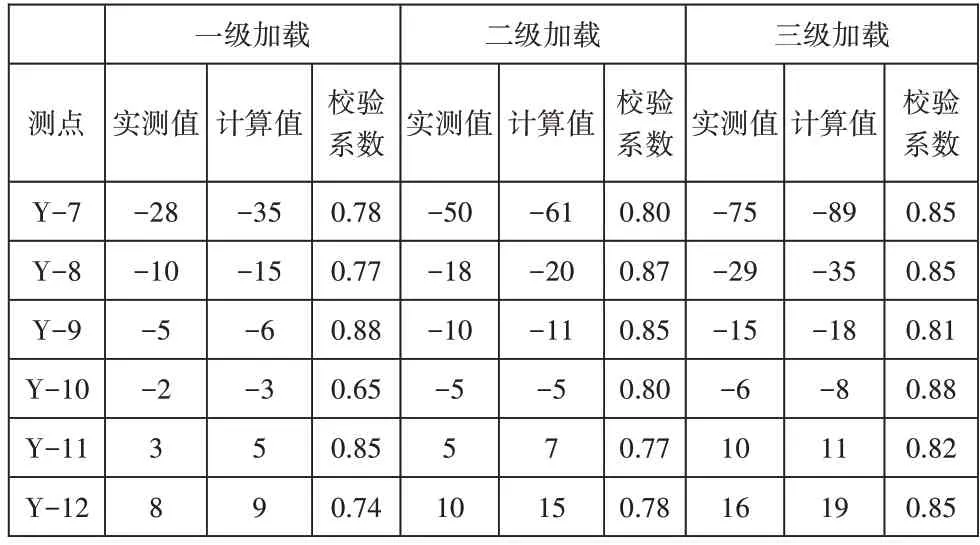
表3 工况二墩顶截面应变试验结果 单位：με

根据表4中试验结果，在工况一作用下，各级试验荷载加载后该预应力混凝土箱梁校验系数取值在0.71～0.82之间，符合规范要求；且跨中实测荷载-挠度曲线[3]基本呈线性变化趋势，桥梁结构基本处于弹性工作状态。

表4 工况一跨中截面挠度试验结果 单位：mm

2.3 基频结果分析

该桥梁多尺度模型、杆系单元模型所采用的理论基频分别为4.07Hz 和4.06Hz，实测基频均为4.78Hz，所以，两种模型计算所采用的基频基本一致，这也验证了多尺度模型的适用性，且实测基频值比有限元模型计算基频值大，表明桥梁刚度符合规范要求。

3 结语

综上所述，应用刚性区法构建桥梁结构多尺度有限元模型能大幅提升杆系单元模型计算精度，并简化桥梁结构整体细化建模过程。通过多尺度模型对桥梁检测过程中重要的控制截面采用实体单元或板壳单元细化建模，所得到的结果也更加切合工程实际，并能得出沿桥梁宽度及高度的应力及变形变化趋势规律，校验系数取值也更加合理，可避免常规杆系单元建模情况下所得到的校验系数取值偏大或偏小的现象。本文所选择的桥梁工程横向宽度小，多尺度模型对于横向宽度较大的桥梁结构也较为适用。