相机标定的金字塔迭代优化算法

李聪亮，宋焕生，穆勃辰，张文涛

长安大学 信息工程学院，西安 710064

近年来，随着交通相机价位持续降低以及计算机视觉领域的迅速发展，在智慧交通系统（intelligent traffic system，ITS）中，交通相机愈发普及，相机标定的重要性不断提高，其主流应用包括车速测量、车辆长宽高测量、车型识别、车流量监控等[1-3]。由于交通相机所获取的是二维图像，不能直接求取三维空间中的物理交通参数，因此需要建立二维坐标系到三维坐标系的映射关系，即相机标定。这是计算机视觉在交通领域应用的基础和最重要的先决条件之一[4-5]。

目前我国ITS中的相机主要分为三种：不可变焦、不可旋转相机，不可变焦、可旋转相机，以及全方位可变焦（pan-tilt-zoom，PTZ）的云台相机。随着云台相机的大范围推广，交通相机也逐步向云台相机更新。由于云台相机的可变焦、可旋转的特性，使得现有单目相机标定方法暴露出两个问题：传统方法在部分旋转角度下误差剧烈增大；传统方法在云台相机旋转过程中相机高度偏差较大。因此传统标定算法优化问题亟待解决。

现有的相机标定主要包含传统的人工相机标定[6]和相机自标定方法[7]两种。人工标定主要分为张氏标定法[8]和消失点标定法[9]；相机自标定算法，一种是在张氏标定法基础上衍生出来的PNP标定法，一种则是在消失点标定法上衍生出来的通过图像处理，自动检测所需先验条件的相机标定算法。考虑到张氏标定法先验条件在交通场景下难以实现，因此本文采用消失点优化方法。

针对交通场景的特殊性，很多学者提出了各种解决办法：Kanhere等人[10]提出了基于一个消失点、两个物理标识和两个消失点、一个物理标识的办法，其中消失点包括沿道路方向、垂直于道路方向和垂直于路平面三个，物理标识包括道路宽度、道路标线长度、相机高度等。该类方法灵活多变，具有较高的适应性，但是在一些特殊角度，如夹角比较小的情况下，误差会急剧提高。Sochor等人[11]提出了一种基于车辆线框模型的标定方法，将Kanhere等人[10]提出的物理标识扩展到车辆本身的长宽高。该方法提高了原有算法的鲁棒性，但是考虑到车辆三维线框获取难度较高且精度较差，同时原有算法的特殊角度误差大的问题并未解决，因此具有较大局限性。Zheng等人[12]提出了一种基于最小二乘约束的道路相机标定模型，该方法基于两个消失点和一条消失线，通过最小二乘约束求取标定参数，得到较好的标定结果。然而在实际交通场景中，第二个方向的消失点难以获取，可适应场景较少，具有较大局限性。Bhardwaj等人[13]提出了基于深度学习的方法，采用DNN网络学习车辆本身具有的关键点特征，并采用滤波和聚合算法求取相机的外参矩阵。该方法通过深度学习求解相机参数，精度较高，但需已知相机内参，不适用于云台相机。朱忆[14]提出了一种基于交通信息流分析的运动消失点获取方式，该方法使用交通流求取消失点，应用场景广泛，但并未解决标定算法中的误差问题，并且考虑到交通流获取消失点过程引起的误差，导致其最终标定精度较差。

综上所述，本文研究了国内外现有的交通场景标定方法后，发现主流标定方法均在Kanhere等人[10]方法上提高鲁棒性或提高先验条件的测量精度，对其方法本身存在的小角度误差急剧增大和相机高度不稳定问题并未解决。

在实验过程中发现，Kanhere等人[10]算法中相机高度和焦距呈现类反比例关系，这对于高度固定的交通相机显然不适合。因此本文提出了一种金字塔迭代优化方案，对基础标定结果在沿道路方向和垂直于道路方向上进行迭代优化，以求解精确、稳定的相机焦距和高度，提高标定精度和稳定性。

1 相关工作

1.1 基础标定模型

与当前主流交通场景下相机标定模型相同，本文将相机简化为针孔模型[15]，假定路面为水平面。参考Kanhere等人[10]的模型，图1（a）为道路场景下相机标定模型的侧视图，图1（b）为道路场景下相机标定模型的侧视图。为方便分析，设相机焦距为f，高度为h，道路宽度为w，偏航角为θ，俯仰角为φ，考虑到交通场景下相机不进行侧倾[13]，因此不予考虑。

本文标定模型中，共定义了3个坐标系：图像坐标系（uv坐标）、相机坐标系（XcYcZc坐标）和世界坐标系（XwYwZw坐标）[16]。图像坐标系原点在图像左上点，u轴与行平行，v轴与列平行；相机坐标系Xc和Yc与图像坐标系平行，Zc为相机光轴。世界坐标系以相机坐标系原点到路平面的垂直投影点为原点，垂直于道路方向为Xw，沿道路方向为Yw，原点正上方指向相机方向为Zw。假设图像像素坐标系上某点坐标为p=[uv1]，该点在世界坐标系下的对应点为x=[x y z1]，比例因子[17]为α。图像到世界坐标系的转换关系为：为外参矩阵，R为旋转矩

其中，K为内参矩阵阵，T为位移矩阵。

由标定模型可知：

式中，u0、v0为图像中心，θ为偏航角，φ为俯仰角。

1.2 基于VWL的标定模型

考虑到交通场景中相机高度无法准确获得，求解第二个方向上的消失点误差较大[18]，本文采用基于VWL的标定模型[19]。下面进行详细推导：

在VWL的模型中，假设沿道路方向上的消失点(u0,v0)、道路宽度w（单车道3.75 m）、道路虚线长度ls和虚线间隔ll（虚线长度为6 m，间隔为9 m），存在世界坐标系中道路平面上某点(x,y,0)，与之对应的图像坐标系中的点为(u,v)，则：

由先验条件得，消失点在世界坐标系中的位置为(-tanθ,1,0)，代入式（3）、（4），得：

将上式转换，得：

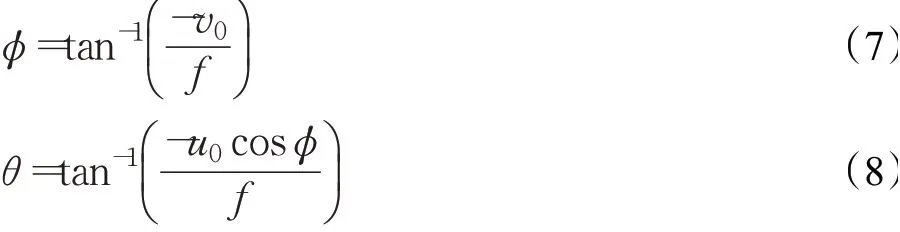
此时，建立关于u0、v0、φ、θ和f的关系式，在式（7）、（8）中共存在3个未知量，因此引入道路宽度w对应的真实距离为ww，图像坐标系中沿道路方向两点(u1,v1)和(u2,v2)之间的虚线距离，对应的真实长度为lw，利用虚线长度和道路宽度的坐标系映射关系，求得：

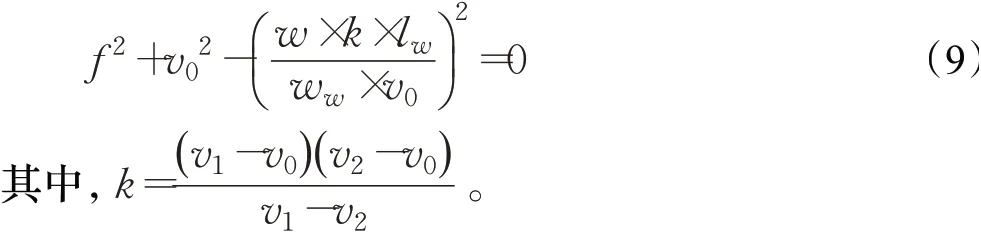
考虑到焦距f必为正值，故得到：

将f代入式（7）、（8），求解得到相机旋转角φ、θ。利用相机模型，反算高度h得：

将f、φ、θ、h代入式（2），得到图像坐标系到世界坐标系的映射关系。

2 基于VWL的优化模型

传统的VWL模型，在相机俯仰角和偏航角发生变动时，存在以下问题：（1）因采用单一道路宽度和标线长度，容易产生局部最优问题；（2）相机高度h与相机焦距f成一种类反比例关系变换，但在旋转过程中焦距不断改变，而高度固定不变，因此不适用于云台相机。因此在本文中，对原有算法进行以下改进：将高度h和焦距f均作为可变参数进行优化，去除原有模型对焦距和高度的约束关系，并将固定不变的道路标线长度和车道宽度作为对比对象，采用迭代求取最小误差的方法求解相机焦距和高度，提升了标定结果的准确性。

世界坐标系以国标作为参照，道路虚线长度为6 m、虚线间隔距离为9 m、单车道宽度为3.75 m。将其作为评判标准，采用枚举试探的方式，求解准确的相机标定结果。详细过程如下：

步骤1假定图像坐标系下，靠近相机一侧车道线上存在两点(un1,vn1)、(un2,vn2)，远离相机一侧的车道线上存在两点(uf1,vf1)、(uf2,vf2)；采用n条虚线（n为正整数）对结果进行优化，每条虚线端点的坐标为{(p2i-1x,p2i-1y),(p2i x,p2i y)|i=1,2,…,n}。根据映射关系，得到世界坐标系下的对应点坐标为(xn1,yn1)、(xn2,yn2)、(xf1,yf1)、(xf2,yf2),

步骤2采用道路标线长度作为沿道路方向的参照物，道路标线长为ls，道路标线间隔为ll，采用n条虚线对结果进行优化。首先求取车道标线预测值{(pre_mark_xi,pre_mark_yi)|i=0,1,…,n}，公式如下所示：

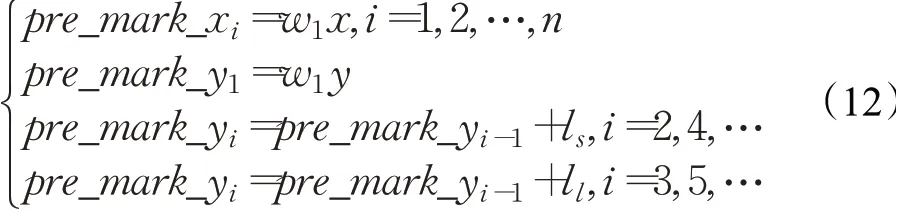
则沿道路方向上的误差为：

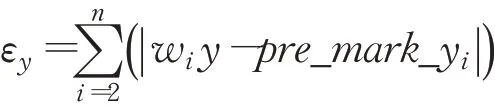
步骤3采用道路宽度作为垂直于道路方向上的参照物，在世界坐标系中求取靠近相机一侧和远离相机一侧车道线方程分别为anearx+bneary+cnear=0、afarx+bfary+cfar=0。利用式（12）求车道标线预测值{(pre_mark_xi,pre_mark_yi)|i=0,1,…,n}，并对每个预测值的横坐标与真实值横坐标对比，同时将预测值的横坐标分别加减单车道宽度w，求得靠近相机一侧和远离相机一侧的预测车道线坐标分别为

步骤4求取预测车道线坐标点到真实车道直线方程的距离l_neari、l_fari，如下式所示：

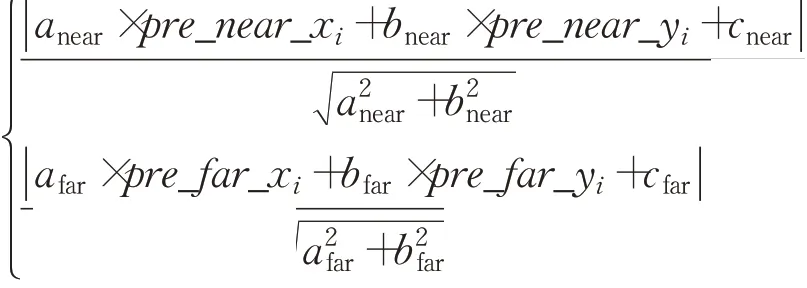
则垂直于道路线方向上的误差为：

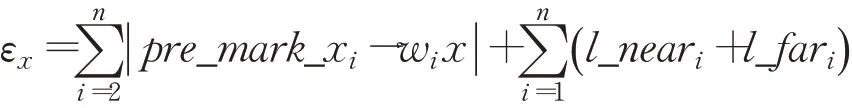
步骤5设基础标定结果为fst和hst，将f和h在[fst-fb,fst+fb]和[hst-hb,hst+hb]区间中进行枚举试探，并设定两个方向的误差阈值为threx、threy，进行初步阈值过滤，得到f和h的集合M={(f0,h0),(f1,h1),(f2,h2),…}。

步骤6设垂直于道路方向上误差εx的权重为weight，对集合M上的每个元素求取综合误差，误差求解如下所示：

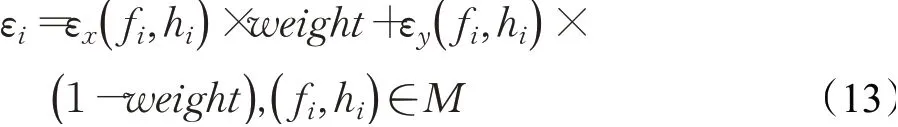
步骤7对集合M中每个元素求取综合误差的最小值εmin，其对应的焦距和高度即为最佳焦距fopt和最佳高度hopt。

本文算法对相机焦距和高度进行二次循环迭代，采用金字塔的迭代方式，二次循环为算法中的最高循环次数，因此本文算法的时间复杂度为O(n2)。本文算法在执行过程中，采用数组对数据进行存储，并且使用了归并排序对数据进行排序，因此本文算法的空间复杂度为O(n)。

3 实验与结果分析

对本文算法进行分组测试，其一为同一场景下，改变相机焦距和旋转角，测试相机高度的稳定性和误差变化；其二为多个不同场景下，测试标定结果的横向误差εx、纵向误差εy和综合误差ε；其三为算法时间消耗和内存消耗的对比。

根据国家标准，单车道宽度为3.75 m，道路虚线长度为6 m，道路虚线间隔为9 m，即：w=3.75 m,ls=6 m,ll=9 m,并取weight=0.5。

选取同一场景中的12个相同相机高度、不同角度的情况，采用传统标定方法和本文方法进行标定，得到相机高度、沿道路方法误差、垂直于道路方向误差、综合误差对比。图2为不同角度下标定结果对比，其中图2（a）为其中3个角度下的原图，图2（b）为传统标定结果，图2（c）为本文迭代优化结果，图中红色线条代表标定后的道路宽度，绿色线条代表标定后的道路标线长度。图3为12个角度下的误差对比，其中图3（a）为沿道路方向45 m的累计误差，图3（b）为垂直于道路线方向37.5 m的累计误差。垂直于道路方向和沿道路方向的误差对比。图4为同场景下综合误差和高度波动对比，其中图4（a）为综合误差对比，图4（b）为相机高度波动对比。

图2 同场景标定结果对比Fig.2 Comparison of calibration results in same scene

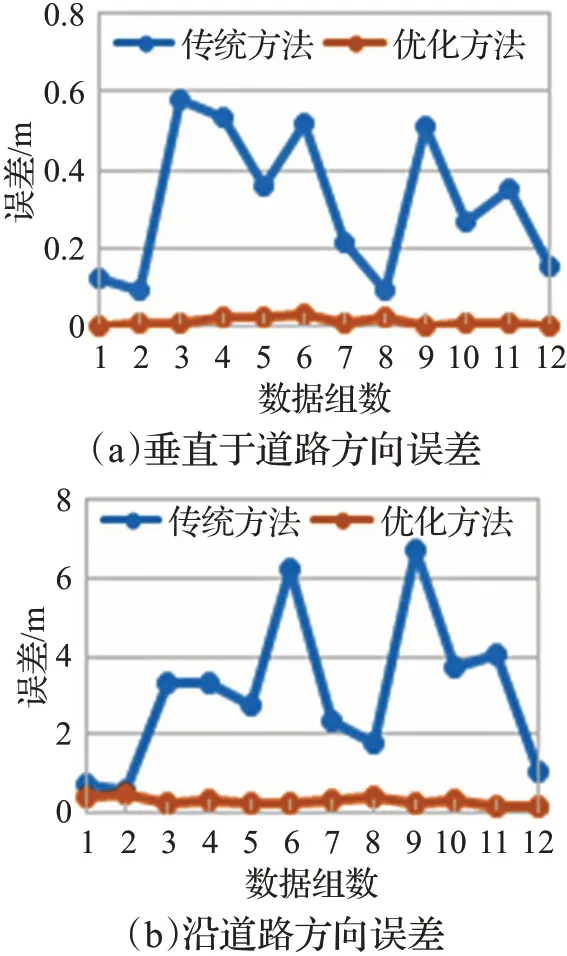
图3 同场景误差对比Fig.3 Same scene error comparison

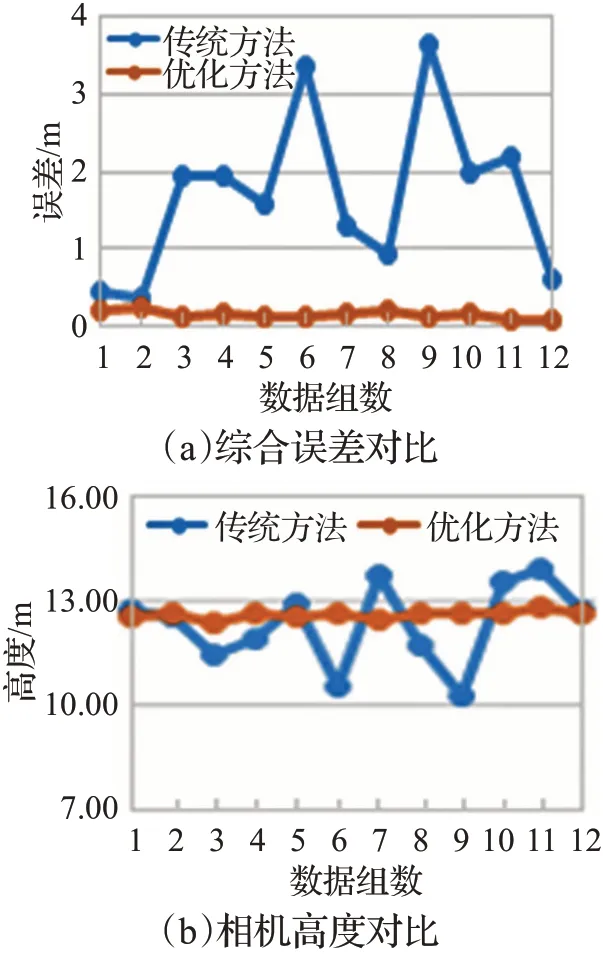
图4 同场景综合误差和高度波动对比Fig.4 Comprehensive error and height fluctuation comparison

表1为12个同场景不同角度下，传统标定方法与本文方法相机标定参数及综合误差对比结果，表2为同场景不同角度下的误差的对比结果。表3为不同角度上的高度对比结果。

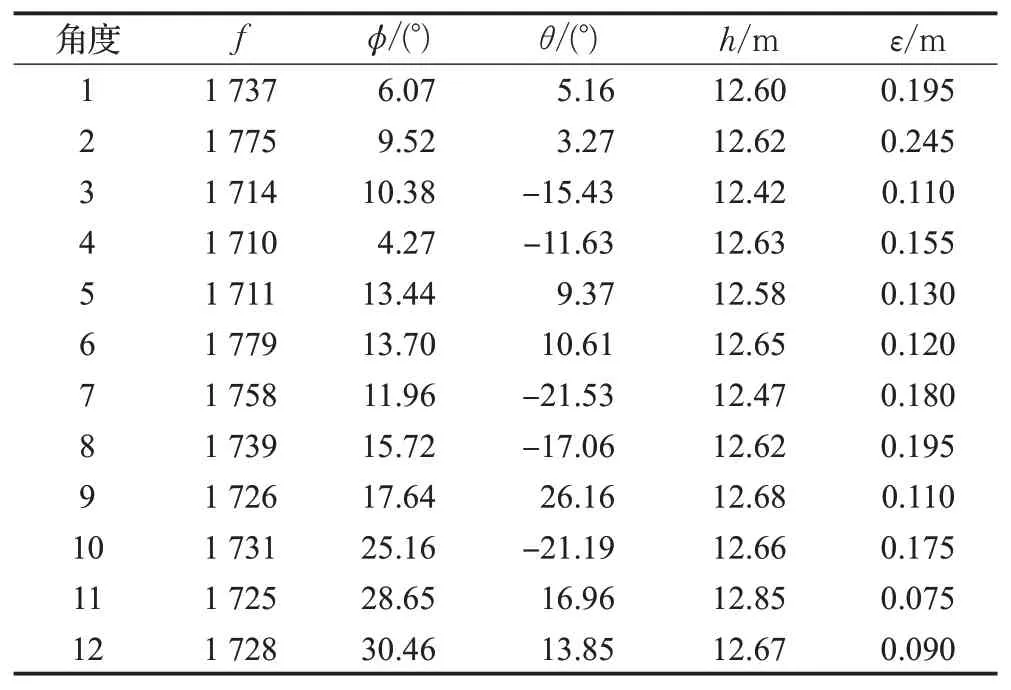
表1 同场景不同角度下标定优化结果及误差Table 1 Calibration optimization results and errors under different angles in same scene

表2 同场景不同角度下方法对比Table 2 Comparison of methods in same scene from different angles 单位：m

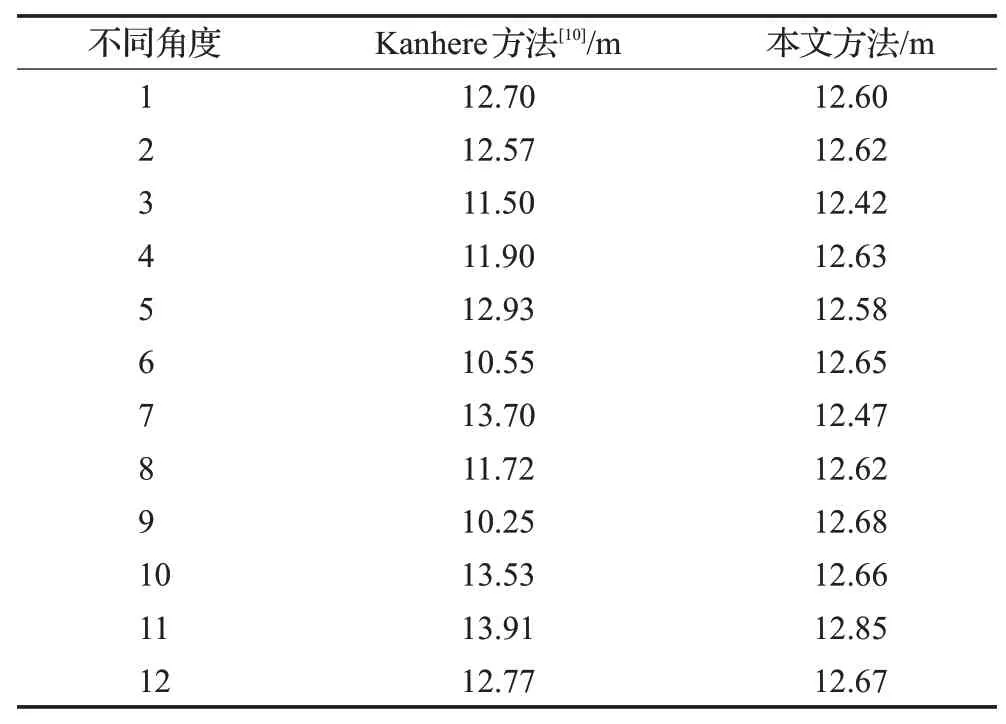
表3 同场景不同角度下高度对比Table 3 High contrast in different angles of same scene

选取12个完全不同的场景，采用传统算法和本文算法进行相机标定，得到沿道路方向误差、垂直于道路方向误差和综合误差对比。图5为其中3个不同场景下的标定结果对比，其中图5（a）为其中3个不同场景原图，图5（b）为传统标定方法误差，图5（c）为本文方法误差，红色线条代表标定后的道路宽度，绿色线条代表标定后的道路标线长度。图6为12个不同场景下的误差对比，其中图6（a）～（c）分别为12个不同场景下沿道路方向、垂直于道路方向及综合误差对比。

图5 不同场景标定结果对比Fig.5 Comparison of calibration results in different scene

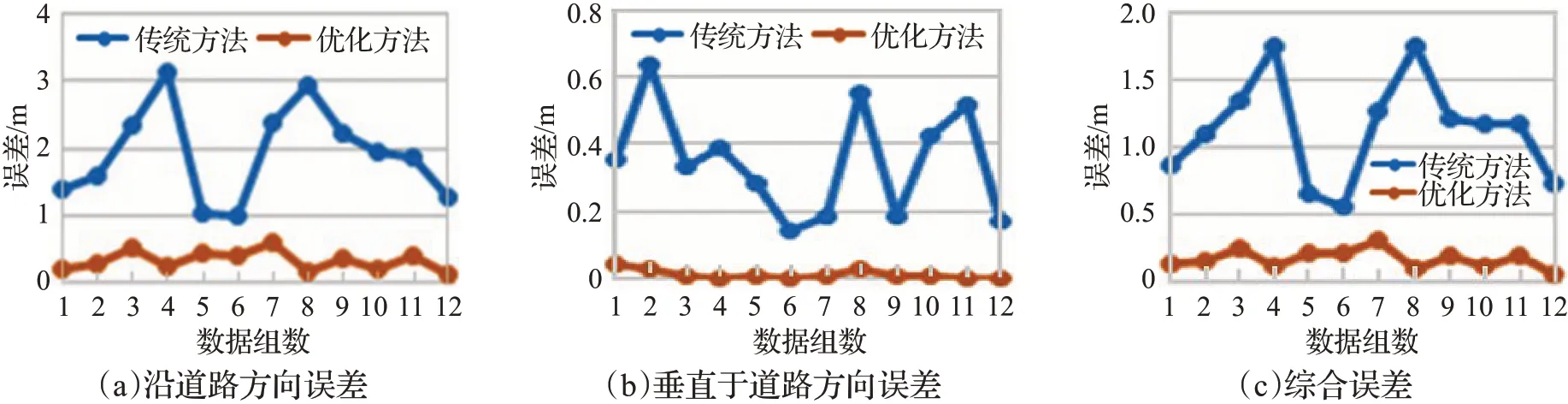
图6 不同场景误差对比Fig.6 Different scene error comparison

表4为12个不同场景下的相机参数及综合误差对比。表5为两种方法对不同场景进行标定时，沿道路方向、垂直于道路方向及综合误差的误差对比。

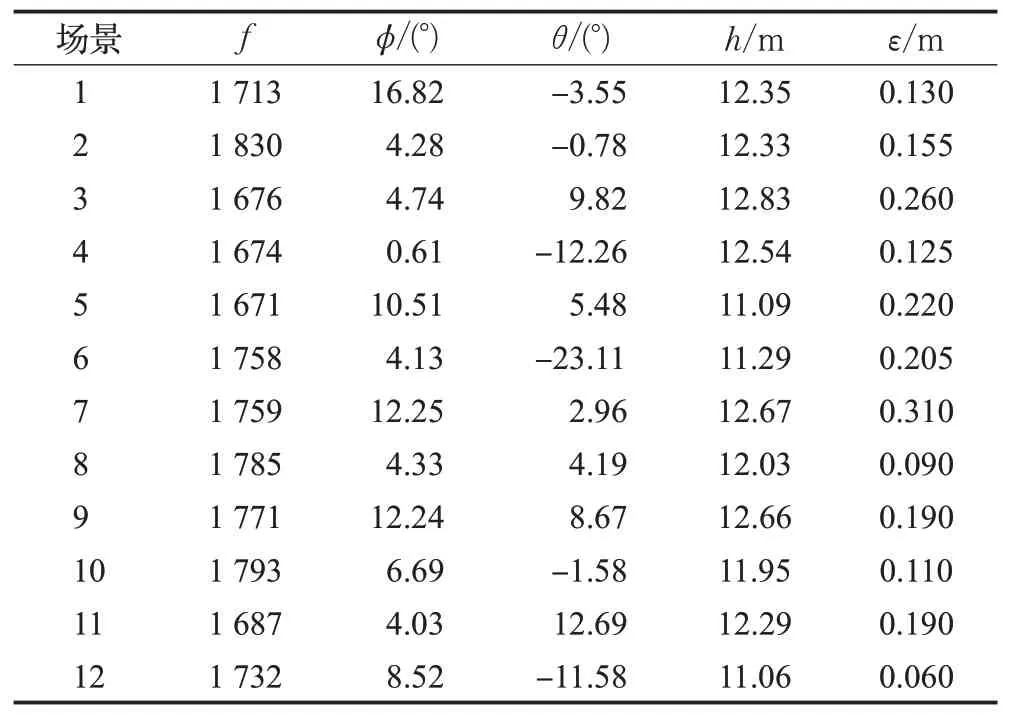
表4 不同场景下标定优化结果及误差Table 4 Calibration optimization results and errors in different scenarios

表5 不同场景下方法对比Table 5 Comparison of methods in different scenarios单位：m

随机选取12个场景，在Inter®CoreTMi7-6800K CPU@3.40 GHz和NVIDIAGeForce GTX 1080Ti上，使 用Kanhere等人[10]方法与本文方法测试，计算两种方法的时间消耗和内存消耗。表6为两种方法时间消耗对比，表7为内存消耗对比。本文方法的时间消耗和内存消耗明显高于Kanhere等人[10]方法，但时间消耗低于1 s，内存消耗低于40 MB，考虑到相机标定算法在实际应用中，仅当相机启动、相机角度或相机焦距改变时调用，因此多余时间消耗和内存消耗在实际应用几乎没有影响。

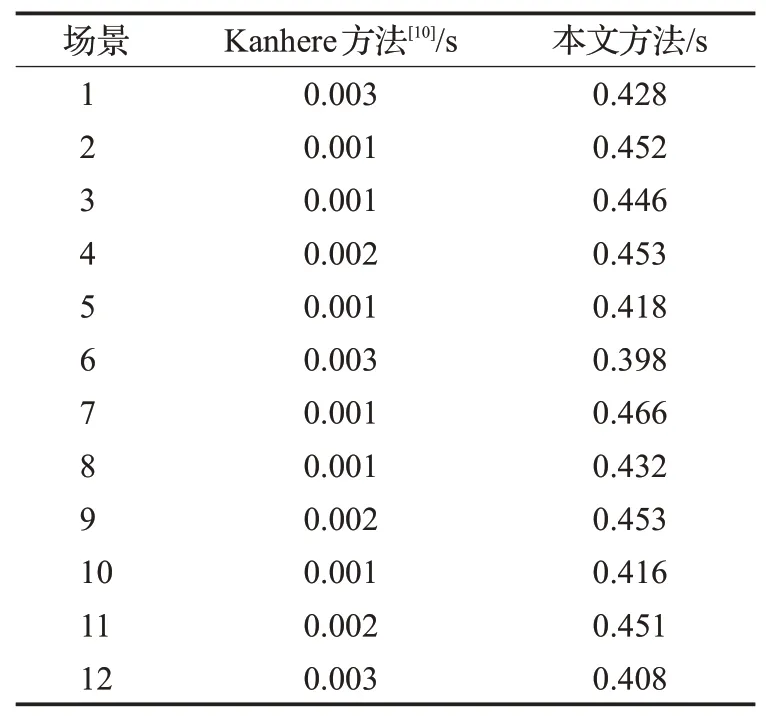
表6 时间消耗对比Table 6 Time consumption comparison

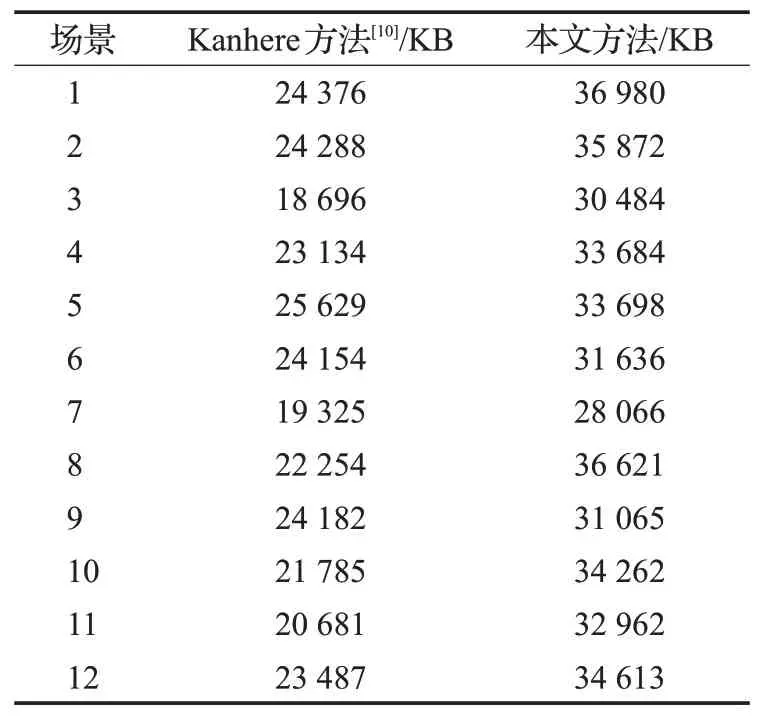
表7 内存消耗对比Table 7 Memory consumption comparison

与传统单消失点算法对比，本文算法具有较高的精度和稳定性，其中，相机高度误差在2%左右，沿道路方向误差低于2%，垂直于道路方向误差低于0.5%，综合误差低于2%。同时本文算法虽增大了时间和内存消耗，但是工程应用中标定算法使用频率较低，因此在实际应用中影响较小。

4 结束语

通过实验验证，在常见交通场景下，本文算法取得了较好的标定结果。本文贡献主要有：（1）通过相机多角度旋转进行标定，一方面通过投票求取相机高度的精确值，另一方面通过相机高度的波动情况来判断标定算法的精度，进一步提高标定结果的稳定性，为云台相机下标定算法的精确度判断提供了一种新的方式；（2）针对先验条件不够精确造成的误差，在三维世界坐标系下，通过沿道路方向和垂直于道路方向上的实际距离进行约束降低误差，提高了标定精度。

本文算法的最小标定条件为一个消失点、道路虚线长度以及道路宽度，其中交通场景下，实际道路虚线长度和道路宽度都为国标，消失点提取可通过车辆轨迹聚类提取，道路虚线和道路宽度则依赖于道路本身，且算法提取精度较人工标定精度较低。未来的工作主要从提高道路虚线和道路宽度的检测精度，在交通场景下寻找更多标识物着手，扩大算法的应用场景，同时减少先验条件不准确造成的误差，提高标定精度。