简支曲梁结构的大变形及吸能分析
2022-10-17霍银磊李梦瑶王惠
霍银磊,李梦瑶,王惠
简支曲梁结构的大变形及吸能分析
霍银磊,李梦瑶,王惠
(河南科技大学 包装工程系,河南 洛阳 471000)
通过对简支曲梁缓冲器的非线性大变形及能量吸收特性的理论研究,为其缓冲设计与应用提供理论参考。基于Euler–Bernoulli梁理论,以曲梁的曲率半径及截面角为基本参数推导简支圆形曲梁大变形控制方程,考虑压板作用下曲梁的多种变形情况给出曲梁的大变形及变形能的解析表达,进而计算不同外力及初始安装角下缓冲器的变形情况及变形能,并与数值计算结果进行对比。理论计算结果与数值解高度吻合,表明计算方法的可靠性,缓冲器的缓冲系数取决于曲梁材料、初始曲率半径及安装角度,与其数量无关;当初始安装角为时,缓冲器的最小缓冲系数可取到6.12。所讨论曲梁缓冲器具有明显的非线性大变形特性和良好的缓冲吸能特性,能够替代传统缓冲材料,方便地用于运输系统的缓冲设计中,给出了简支曲梁缓冲器的基本设计方法。
简支曲梁;缓冲结构;大变形;缓冲性能
目前广泛应用的缓冲材料主要有塑料基的泡沫塑料、气泡膜、气柱袋等以及纸基的蜂窝纸板、瓦楞纸板、纸浆模塑等。此2类材料要么难以降解,要么以结构的不可逆破坏来吸收冲击能量而难以重复使用[1],因此,具有良好回弹性的缓冲机构或结构受到越来越多的关注,例如应用于精密仪器及高速重复冲击缓冲场合的气囊类缓冲系统[2]、油气缓冲器[3]、弹性支撑缓冲系统[4]、恒力缓冲装置[5]以及以磁流变阻尼[6]为代表的半主动式缓冲技术等。此类缓冲结构或机构大都具有较强的非线性变形特性,具有较大的平台应力或者恒力区间,能够在变形过程中吸收大量的能量,但其组成一般较为复杂,广泛应用受到限制。相对而言,Pham等[7]曾经利用曲梁设计了一个可在区间内输出恒力的稳态机构用于过载保护和力控制系统,为曲梁机构的缓冲应用提供了借鉴。松田技术研究所[8]基于曲梁开发了用于大型精密仪器运输减震的金属球状减震器,其试验结果表明减震器实现了减震98.5%的效果,但研究没有涉及到对其大变形及冲击能量吸收特性的理论或者实验分析。
对于曲梁的大变形分析已取得大量可喜的成果:赵跃宇等[9]详细地评述了国内外曲线梁的研究进展情况,概述了曲梁静动力学的基本理论、建模及分析方法、面内面外振动及分析方法、非线性问题及分析方法。近年来,曾森等[10]分析和总结了前人研究成果,对曲梁相关方程做了更具普遍性的分析,给出了数学上更严密的结果。李卓庭等[11]考虑曲梁微段的面内变形和面外变形,对曲梁的几何方程进行了严格的推导和阐述。Lin等[12-14]分别利用拉格朗日和欧拉描述分析了层合曲梁的有限变形,给出了圆曲线和螺旋曲线叠合梁的解析解。基于类似方法,周勇等[15]对压电层合曲梁在力电载荷下的有限变形进行了分析,以梁曲率半径和弧切角为基本参数推导了压电曲梁在外载荷作用下的控制方程,计算了圆弧层合曲梁的非线性变形。Batista[16]给出了自由端受到力矩和倾斜力作用的悬臂直梁的精确Jacobi椭圆函数的解析解。万泽青等[17]基于一阶剪切变形理论和轴线可伸长的精确几何非线性理论,推导了变曲率曲梁在热机载荷作用下的几何非线性控制方程。
为简化计算,诸多数值方法也被应用于曲梁大变形问题的求解中:Surana[18]利用有限节点法和全拉格朗日方法给出了二维曲梁单元的几何非线性公式。吕和祥等[19]借助Lagrange(T.L.)法、修正的Lagrange(U.L.)法及带有动坐标的迭代法求解梁的几何非线性问题。蔡松柏等[20]首次采用共旋坐标法导出了平面梁单元发生大转动小应变时的非对称单元切线刚度矩阵,由Newton-Raphson迭代法获得了大转动梁、方形和圆形框架的高精度数值解。李世荣团队[21-23]基于打靶法分别研究了框架结构的大变形平衡构形、功能梯度变曲率曲梁在机械和热载荷共同作用下弯曲变形、沿轴线均布切向随动载荷作用下的非线性平面弯曲问题以及悬臂半圆形曲梁在沿轴线均布的切向随动载荷作用下的非线性平面弯曲问题。Sharifnia[24]采用梁截面斜角和轴线长度作为主要参数,提出了一种简单而有效的有限元方法来分析平面静力问题中直线型和曲线欧拉伯努利梁的大挠度。
文中针对松田技术研究所设计的球形减震器,讨论其受压时的大变形情况并探讨其缓冲应用。文中将基于Euler–Bernoulli梁理论建立曲梁的大变形平衡方程,考虑准静态压力作用下曲梁的非线性大变形特性,分析端部简支的曲梁球形缓冲结构发生大变形时的位形及能量吸收特性。以期为曲梁结构的缓冲设计及应用提供参考。
1 曲梁的一般方程及大变形分析
1.1 曲梁缓冲器模型
考虑图1a的松田曲梁结构球形缓冲器,置于上下压板间的曲梁结构高度为,两端简支单根细长曲梁(图1b)截面厚度,宽度,安装端未变形截面角(轴线切向与轴的夹角)为L,简支曲梁两端约束于轴并在压板上的竖直外力作用下发生弯曲变形。
1.2 曲梁的一般方程
(1)
根据Euler‒Bernoulli梁理论,忽略曲梁的轴向伸长,处曲梁微元可表示为:
(2)
式中:、分别为曲梁变形前后的曲率半径。
曲梁变形后的几何关系:
,
,
(3)
,
(4)
图1 松田的球形缓冲器及曲梁力学模型
Fig.1 Spherical shock absorber of Matsuda and mechanical model of simply supported curved beam
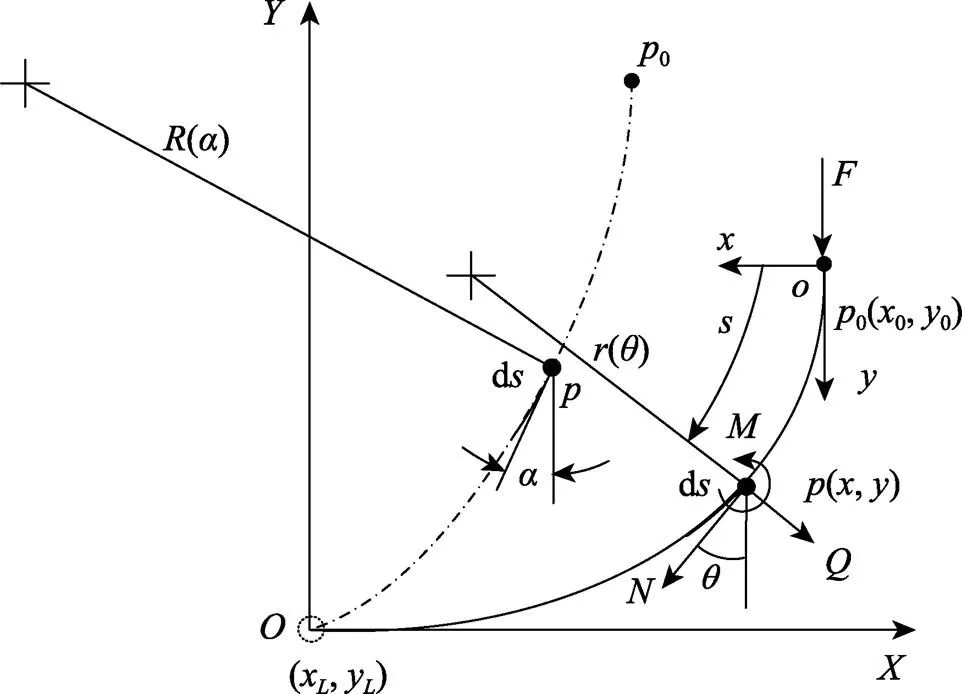
图2 一般曲梁的变形分析
,
,
(5)
由式(5)得曲梁变形控制方程:
(6)
(7)
式(7)有通解:
(8)
对于末端简支曲梁,末端弯矩恒为0,因此有边界条件:
,
(9)
由式(8)及边界条件(9)即可求得:
(10)
式(10)分离变量并两边积分得到关系:
(11)
(12)
及曲梁的变形能:
(13)
1.3 一般曲梁的变形分析
忽略压板的作用,假设竖直外力直接作用于曲梁末端。考虑一般简支半圆曲梁的大变形问题(),得到不同竖直外力作用下变形后曲梁的截面角及整根曲梁的大变形位形图(图3),由图3可见随着压力的增大,曲梁末端截面角逐渐增大,曲梁末端纵向位移也逐渐增大;当压力不为0时,变形后的曲梁截面角随着的增大而非线性增大,体现了大变形曲梁的非线性特性。基于打靶法[19-23]的曲梁大变形数值解一并在图3中给出。可见文中解析解与数值解吻合的很好,证明了文中解析解的可靠性。
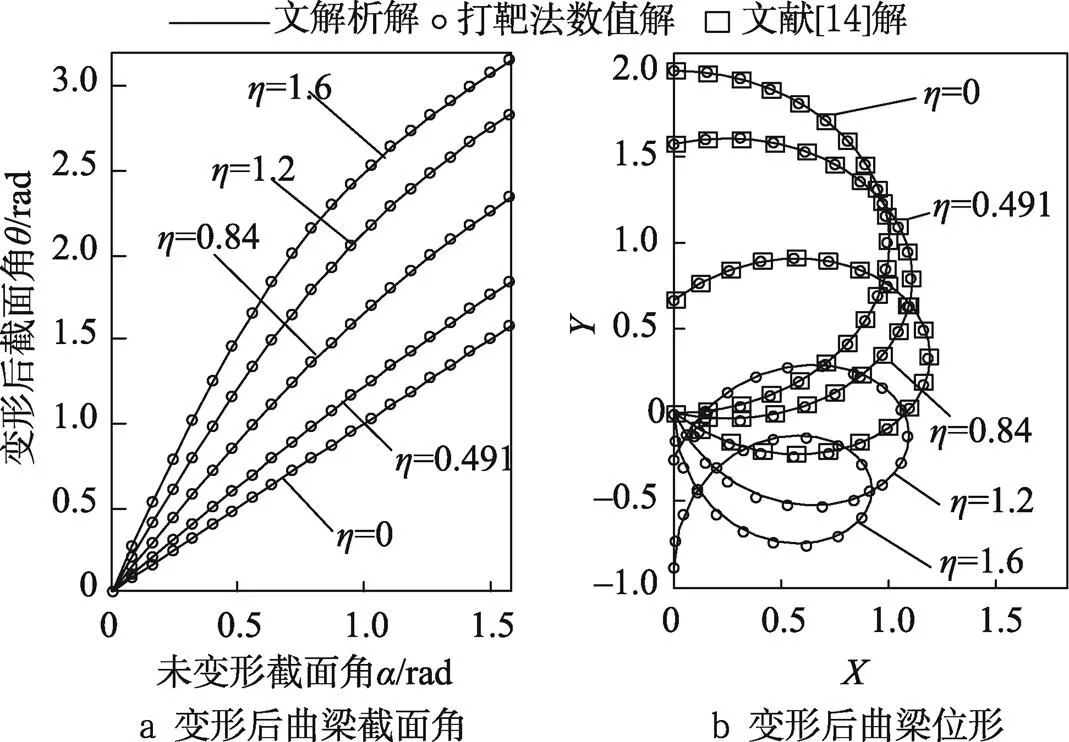
图3 一般半圆简支曲梁的压缩特性(,)
2 压板间曲梁的变形分析
对于安装在上下压板之间的曲梁结构,曲梁在压板压力作用下的高度变为(图4),当压力较小时,,压力作用点位于曲梁端部,曲梁变形情况与1.2节中情况相同;随着压力的增大,当时,此时曲梁受力点离开其末端向其中部转移;随着压力的进一步增大,曲梁两末端接触并相互挤压,因此,对于压板间曲梁缓冲结构的大变形分析应分别考虑3种不同的情况。
(14)
此时曲梁位形及受力情况见图5,曲梁段发生弯曲变形,段自由。
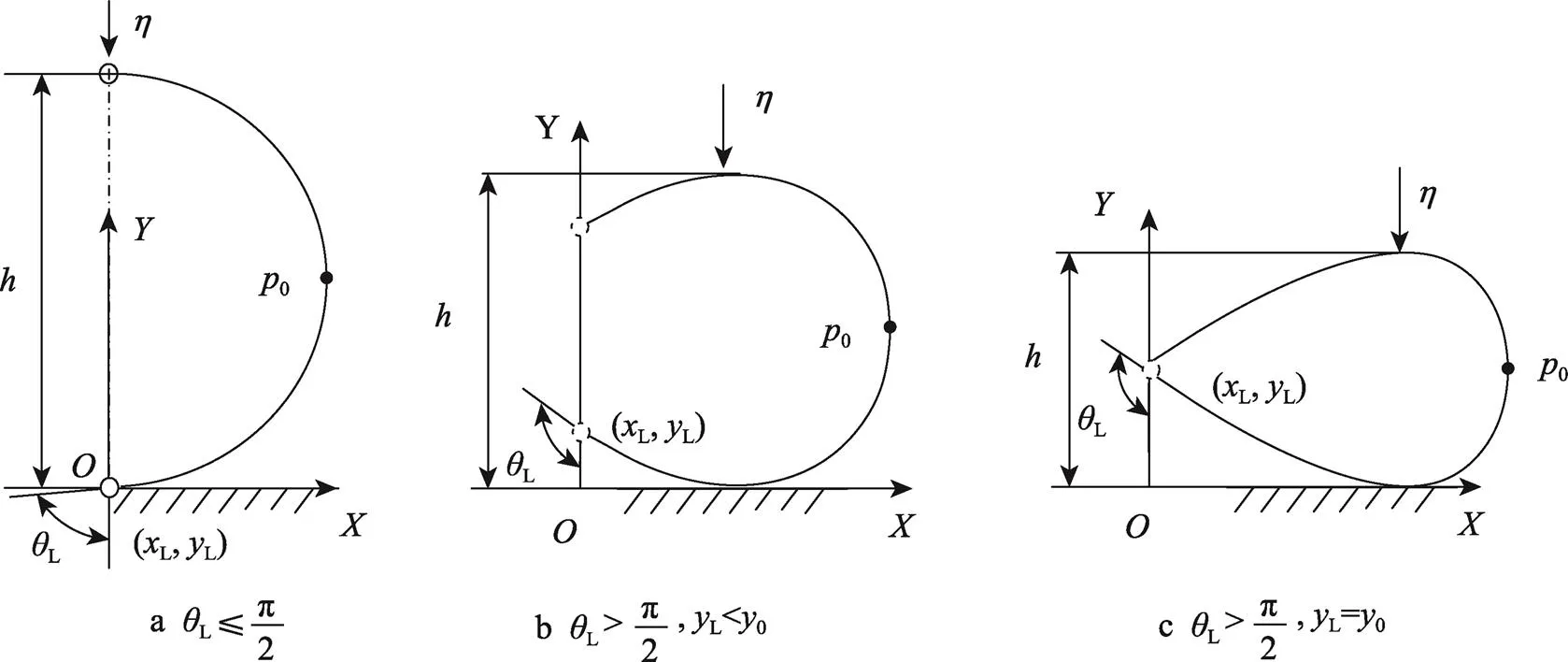
图4 压板间曲梁的变形情况
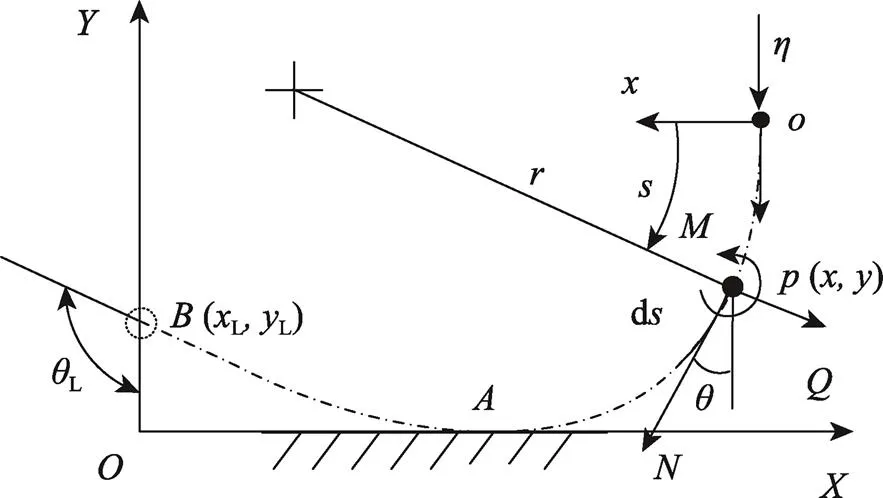
图5 情况2曲梁变形及微段受力分析
,
(15)
,(16)
(17)
(18)
(19)
因此,利用式(12)—(13),曲梁上任意点的位置及变形能可分别写为:
(20)
(21)
(22)
此时曲梁位形及受力情况如图6所示,曲梁段、段均发生弯曲变形。
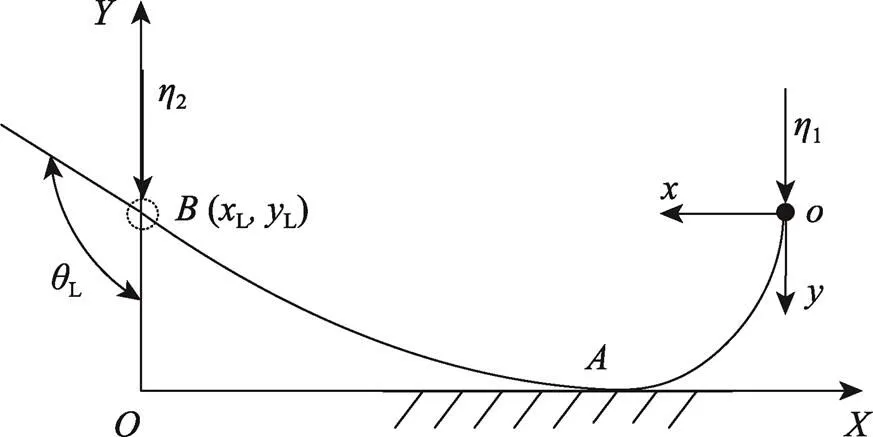
图6 情况c曲梁变形及受力情况
,
,
(23)
(24)
(25)
(26)
由式(26)及边界条件(23)的第3式得:
(27)
(28)
再加上关系:
(29)
3 分析与讨论
3.1 曲梁的大变形位形
图7给出了半圆曲梁在压板作用下的变形情况,其中曲梁初始安装角,由式(14、22)分别可得、。由图7可见变形后曲梁的截面角随着的增大而增大:当时,,随着的增大而非线性增大,压力越大的增大也越快,对应的末端截面角也越大;此时压板对曲梁压力的作用点位于曲梁端部。
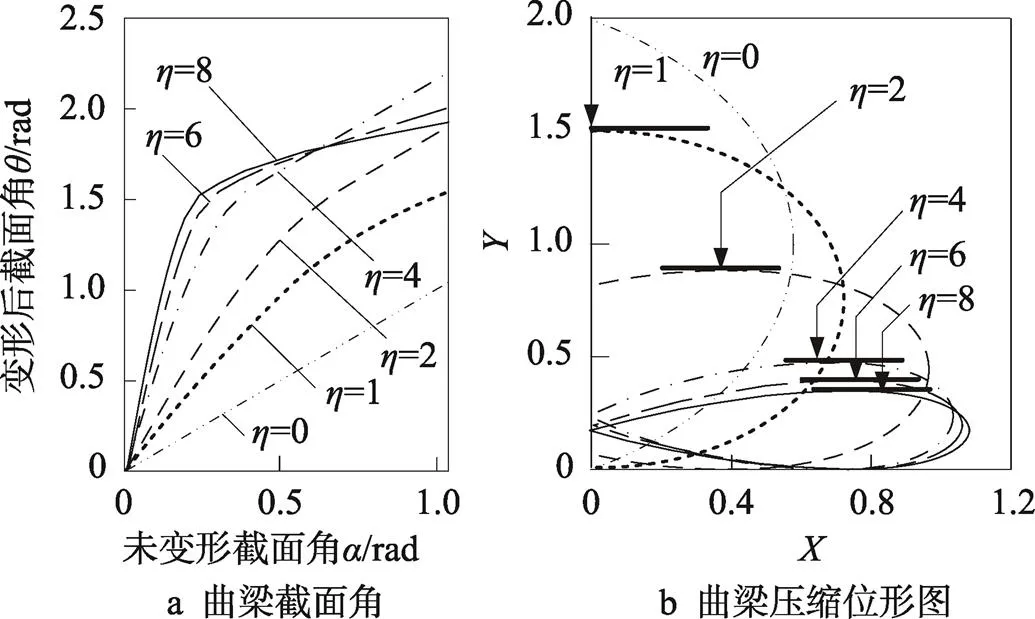
图7压板间简支曲梁的压缩变形特性(,)
3.2 曲梁结构的变性能及缓冲系数
如果不考虑机械能的损失,曲梁结构组成的缓冲器在受到冲击作用时,全部冲击能量都转化为曲梁的变形能。因此,在一定的外力作用下曲梁缓冲器的变形能越大代表其所吸收的冲击能量也就越大。冲击过程中作用在曲梁缓冲器上的压力及在此压力下曲梁结构的变形量(上压板位移)及变形能可分别表示为:
,
,
(30)
其中:分别为组成曲梁缓冲器的曲梁数目。
对于高度为的曲梁缓冲器,借鉴对实体材料的能量吸收评价方法[25],曲梁缓冲器的缓冲系数可表示为:
(31)
其中为作用于单根曲梁上的冲击力,由式(31)可见缓冲器的缓冲系数与曲梁数量m无关,仅取决于曲梁的初始高度H和曲率半径R(或初始安装角αL);对于给定的冲击力,缓冲器的变形能越大,缓冲系数C就越小。图8给出了具有不同初始安装角αL的曲梁缓冲器的力–变形曲线及缓冲系数曲线,可见曲梁缓冲器受压时体现出类似于实体缓冲材料的明显的非线性变形特性,力–变形曲线具有较为明显的平台阶段;随着冲击压力的增大缓冲系数曲线也有明显的极小值出现。曲梁末端初始安装角αL越小,缓冲器的平台阶段越明显,缓冲系数的极小值也越小:当时,缓冲系数的极小值取到。
图8 压板间曲梁的压缩特性及缓冲系数()
Fig.8 Compression characteristics and cushioning coefficients of simply supported curved beams between platens ()
3.3 曲梁缓冲器的设计
在产品的缓冲设计中,如果已知产品不发生破坏所能够承受的最大冲击力max以及缓冲器的安装空间(即缓冲器的高度),再利用图8b的最小极小值点即可快速确定曲梁的最佳安装角L及的作用在单根曲梁上的冲击力,进而确定曲梁的数目。当然,也可以根据缓冲器初始高度及安装角L由图8b的对应曲线的最低点找到单根曲梁承受的冲击力,进而确定曲梁的数目。
4 结语
文中针对曲梁结构缓冲装置,基于Euler–Bernoulli梁理论建立了以曲率半径和截面角为基本参数的平板压力作用下曲梁的大变形平衡方程,给出了压板作用下曲梁发生大变形时的位形的解析表达,并与打靶法数值解进行了对比,解析解与数值解吻合较好。压板间曲梁的变形情况较为复杂,随着压力的增大,曲梁所受压力作用点逐渐由端部向中部移动,其力–变形曲线具有明显的非线性特性。随着安装角的减小,在相同的平板压力作用下,结构的变形也越小,力–变形曲线表现出更明显的平台阶段,相对应的最小缓冲系数也越小,缓冲性能越好。在明确了产品能够承受的最大冲击力及允许的缓冲空间的情况下,可方便地利用曲梁的缓冲系数曲线进行曲梁缓冲器的各参数设计。
[1] 鄂玉萍, 王志伟. 纸质缓冲材料能量吸收特性研究进展[J]. 振动与冲击, 2010(5): 40-45.
E Yu-ping, WANG Zhi-wei. Advance in Study on Energy-Absorbing Property of Paper-Based Cushion Packing Materials[J]. Journal of Vibration and Shock, 2010(5): 40-45.
[2] 温金鹏, 李斌, 杨智春. 缓冲气囊冲击减缓研究进展[J]. 宇航学报, 2010, 31(11): 2438-2447.
WEN Jin-peng, LI Bin, YANG Zhi-chun. Progress of Study on Impact Attenuation Capability of Airbag Cushion System[J]. Journal of Astronautics, 2010, 31(11): 2438-2447.
[3] 刘洪权, 闫明, 张春辉, 等. 新型缓冲阻尼器设计及其冲击响应特性研究[J]. 振动与冲击, 2020, 39(4): 291-298.
LIU Hong-quan, YAN Ming, ZHANG Chun-hui, et al. Design of a Retrofitted Damper and Its Shock Response Characteristics[J]. Journal of Vibration and Shock, 2020, 39(4): 291-298.
[4] 严国平, 彭震奥, 钟飞, 等. 精密包装弹性支撑缓冲系统振动特性修正模型及分析[J]. 振动与冲击, 2021, 40(22): 251-258.
YAN Guo-ping, PENG Zhen-ao, ZHONG Fei, et al. Correction Model and Analysis of Vibration Characteristics of a Precision Packaging Elastic Support Cushioning System[J]. Journal of Vibration and Shock, 2021, 40(22): 251-258.
[5] 张春辉, 汪玉, 杜俭业, 等. 被动式恒力缓冲装置的设计与性能研究[J]. 振动与冲击, 2015, 34(13): 176-181.
ZHANG Chun-hui, WANG Yu, DU Jian-ye, et al. Design of a Passive Constant Force Shock Absorber and Its Characteristics[J]. Journal of Vibration and Shock, 2015, 34(13): 176-181.
[6] 寿梦杰, 廖昌荣, 叶宇浩, 等. 冲击载荷下磁流变缓冲器的动力学行为[J]. 机械工程学报, 2019, 55(1): 72-80.
SHOU Meng-jie, LIAO Chang-rong, YE Yu-hao, et al. Dynamic Behavior of Magnetorheological Energy Absorber under Impact Loading[J]. Journal of Mechanical Engineering, 2019, 55(1): 72-80.
[7] PHAM H T, WANG D A. A Constant-Force Bistable Mechanism for Force Regulation and Overload Protection[J]. Mechanism and Machine Theory, 2011, 46(7): 899-909.
[8] 松田技術研究所. 防震器(金属球状)[EB/OL]. 2013–01–01. http://www.mrd-matsuda.co.jp/airsus_metal. html.
MATSUDA R&D CO., LTD. Shock Absorber (Metal Ball)[EB/OL]. 2013–01–01. http://www.mrd-matsuda.co.jp/ airsus_metal.html.
[9] 赵跃宇, 康厚军, 冯锐, 等. 曲线梁研究进展[J]. 力学进展, 2006, 36(2): 170-186.
ZHAO Yue-yu, KANG Hou-jun, FENG Rui, et al. Advances of Research on Curved Beams[J]. Advances in Mechanics, 2006, 36(2): 170-186.
[10] 曾森, 陈少峰, 曲婷, 等. 大位移小转角空间曲梁的弹性力学方程[J]. 工程力学, 2010, 27(12): 14-20.
ZENG Sen, CHEN Shao-feng, QU Ting, et al. Elasticity Equations for Spatial Curved Beams with Large Displacement and Small Rotation[J]. Engineering Mechanics, 2010, 27(12): 14-20.
[11] 李卓庭, 宋郁民. 曲梁几何方程推导[J]. 工程力学, 2019, 36(S1): 12-16.
LI Zhuo-ting, SONG Yu-min. Geometric Equation Derivation of Curved Beam[J]. Engineering Mechanics, 2019, 36(S1): 12-16.
[12] LIN K C, HSIEH C M. The Closed form General Solutions of 2-D Curved Laminated Beams of Variable Curvatures[J]. Composite Structures, 2007, 79(4): 606-618.
[13] LIN K C, LIN C W, et al. Finite Deformation of 2-D Curved Beams with Variable Curvatures [J]. Journal of Solid Mechanics & Materials Engineering, 2009, 3(6): 876-886.
[14] LIN K C, LIN C W. Finite Deformation of 2-D Laminated Curved Beams with Variable Curvatures[J]. International Journal of Non-Linear Mechanics, 2011, 46(10): 1293-1304.
[15] 周勇, 李荣华, 李实, 等. 压电层合曲梁大变形的精确分析[J]. 压电与声光, 2016, 38(1): 88-93.
ZHOU Yong, LI Rong-hua, LI Shi, et al. Precise Analysis of the Finite Deformation of Curved Beams Covered with PZT Actuators[J]. Piezoelectrics & Acoustooptics, 2016, 38(1): 88-93.
[16] BATISTA M. Analytical Treatment of Equilibrium Configurations of Cantilever under Terminal Loads Using Jacobi Elliptical Functions[J]. International Journal of Solids and Structures, 2014, 51(13): 2308-2326.
[17] 万泽青, 李世荣, 马洪伟. 基于一阶剪切变形理论的变曲率曲梁的几何非线性方程[J]. 应用力学学报, 2018, 35(5): 983-987.
WAN Ze-qing, LI Shi-rong, MA Hong-wei. Geometrically Nonlinear Equations of Curved Beams with Variable Curvatures Based on the First-Order Shear Deformation Theory[J]. Chinese Journal of Applied Mechanics, 2018, 35(5): 983-987.
[18] SURANA K S. Geometrically Non-Linear Formulation for Two Dimensional Curved Beam Elements[J]. Computers & Structures, 1983, 17(1): 105-114.
[19] 吕和祥, 朱菊芬, 马莉颖. 大转动梁的几何非线性分析讨论[J]. 计算结构力学及其应用, 1995, 12(4): 485-490.
LYU He-xiang, ZHU Ju-fen, MA Li-ying. Discussion of Analysing of Geometric Non-Linear Beams with Large Rotations[J]. Chinese Journal of Computational Mechanics, 1995, 12(4): 485-490.
[20] 蔡松柏, 沈蒲生. 大转动平面梁有限元分析的共旋坐标法[J]. 工程力学, 2006, 23(S1): 69-72.
CAI Song-bai, SHEN Pu-sheng. co-Rotational Procedure for Finite Element Analysis of Plane Beam under Large Rotational Displacement[J]. Engineering Mechanics, 2006, 23(S1): 69-72.
[21] 李世荣, 宋曦, 周又和. 弹性曲梁几何非线性精确模型及其数值解[J]. 工程力学, 2004, 21(2): 129-133.
LI Shi-rong, SONG Xi, ZHOU You-he. Exact Geometrically Nonlinear Mathematical Formulation and Numerical Simulation of Curved Elastic Beams[J]. Engineering Mechanics, 2004, 21(2): 129-133.
[22] 万泽青, 李世荣. 功能梯度变曲率曲梁的几何非线性模型及其数值解[J]. 固体力学学报, 2015, 36(3): 204-214.
WAN Ze-qing, LI Shi-rong. Geometrically Nonlinear Model and Numerical Simulation of Functionally Graded Variable Curvature Curved Beam[J]. Chinese Journal of Solid Mechanics, 2015, 36(3): 204-214.
[23] 张沫. 功能梯度材料曲梁及简单平面框架结构非线性大变形分析[D]. 扬州: 扬州大学, 2013: 13-18.
ZHANG Mo. Nonlinear Large Deformation Analysis of Curved Beam and Simple Plane Frame Structure with Functionally Graded Materials[D]. Yangzhou: Yangzhou University, 2013: 13-18.
[24] MAHDI S. A New Beam Element for Analysis of Planar Large Deflection[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2018, 40(2): 1-9.
[25] 彭国勋. 运输包装[M]. 北京: 印刷工业出版社, 1999: 96-98.
PENG Guo-xun. Packing for Transport[M]. Beijing: Printing Industry Press, 1999: 96-98.
Analysis of Large Deformation and Energy Absorption of Simply Supported Curved Beam
HUO Yin-lei,LI Meng-yao, WANG Hui
(Department of Packaging Engineering, Henan University of Science and Technology, Henan Luoyang 471000, China)
The work aims to study the nonlinear large deformation and energy absorption characteristics of the shock absorber formedby simply supported curved beam to provide theoretical reference for shock absorber design and application. Based on Euler-Bernoulli beam theory, the control equation of large deformation of simply supported circular curved beam was derived, in which the curvature radius and section angle were selected as the basic parameters of the control equation. The large deformation and deformation energy of the simply supported curved beam were analytically expressed considering various deformation conditions of the curved beam under the action of the platens, and then the deformation conditions and deformation energy of the shock absorber under different external forces and initial installation angles were calculated and compared with the numerical results. The high agreement between the theoretical results and the numerical solution showed the reliability of the calculation method. The cushion coefficient depended on the material, radius of curvature and initial installation angle, and had nothing to do with the quantity of beam. When the initial installation angle was, the minimum cushion coefficient of the shock absorber could reach 6.12. The simply supported curved beam shock absorber has obvious nonlinear large deformation characteristics and good energy absorption characteristics. It can be used to replace the traditional shock absorption materials and is convenient to be used in shock absorption design of transport system. The basic design method of simply supported curved beam shock absorber is given.
simply supported curved beam; cushion structure; large deformation; cushioning performance
TB121;TB485.1
A
1001-3563(2022)19-0190-08
10.19554/j.cnki.1001-3563.2022.19.022
2022–01–09
国家自然科学基金(11972286)
霍银磊(1979—),男,博士,讲师,主要研究方向为包装动力学、机械动力学。
责任编辑:曾钰婵
