AGV 停车库临时存放区优化设计仿真研究

彭浩荣，吴艳一 PENG Haorong, WU Yanyi

（1. 同济大学建筑设计研究院（集团） 有限公司，上海 200092；2. 上海智慧交通安全驾驶工程技术研究中心，上海 200092；

3. 上汽大众汽车有限公司，上海 201800）

0 引 言

随着我国汽车保有量的不断增长，城市“停车难”问题日益凸显。如何利用有限的土地资源增加停车位，如何提高停车场的使用效率以及提升停车的便利性，是当前城市交通发展中急需解决的关键问题。AGV（Automated Guided Vehicle, 自动导引车） 是指装备有自动导航装置，能够沿着导航路径行驶，并具有可编程、安全保护以及各种移载功能的运输车，是柔性生产线和立体库等现代物流仓储体系的关键设备之一。近年来，AGV 机器人在停车领域的应用快速发展，目前在南京、北京、上海、广州、重庆等地均有已经建成使用的AGV 智能停车库。驾驶人仅需在智能平台进行操作，AGV 停车机器人即能自动完成车辆的存放和提取，极大地提高了停车的便利性。此外，相比于传统停车库，AGV 停车库还具有停车效率高、空间利用率大等优点，是目前缓解城市停车难问题的重要手段。

从已经开展运营的案例来看，AGV 智能停车库除了内部类似于“汽车仓库”的区域之外，还需要供驾驶人临时停放、锁车、取车的临时存放区。已有的针对AGV 智能停车库的相关研究，主要集中在AGV 停车机器人的定位导航、路径规划、调度算法等方面，而对AGV 停车库临时存放区的合理有效设置等问题目前鲜有研究。但是，临时存放区是AGV 机器人停车区域与驾驶人存取车操作的关键过渡区域，临时存放区设置不当可能造成效率瓶颈或者空间资源浪费，对AGV 停车库的整体运行效果具有重要的影响，因此，有必要对临时停放区的优化设计进行研究。

本文采用元胞自动机（Cellular Automata，CA） 方法对AGV 停车库的临时存放区优化设计进行了仿真研究，基于某城市综合体的地下停车场，建立了AGV 停车库CA 仿真模型，通过车辆平均延误、最大排队长度等指标评估了5 种临时存放区设置方案的运行效果。本文建立的CA 仿真模型及研究结果能够为AGV 停车库的优化设计提供参考，有助于提高AGV 停车技术的有效应用，对改善城市停车难问题具有重要的积极作用。

1 AGV 停车库CA 仿真模型

1.1 元胞自动机模型

元胞自动机（Cellular Automata，CA） 模型主要由元胞、元胞空间、元胞邻居和演化规则四部分构成，是一种时间、空间和状态都离散的网格动力学模型。其中每个元胞根据当前时刻自身及邻域元胞的状态进行下一时刻的状态更新，即有：

1.2 AGV 停车库仿真模型

根据已运营的AGV 停车库相关资料，AGV 停车库主要分为等待区、临时存放区、停车机器人内部操作区三个区域。在本文研究中，不涉及停车机器人的定位导航、路径规划和调度策略等问题，因此不对停车机器人在内部操作区的具体运行进行模拟，内部操作区与临时存放区的交互通过停车、取车模型进行设置。

1.2.1 外部通道车辆行驶模型

车辆在AGV 停车区外部通道的行驶模型如图1 所示。白色格子处为外部等待区，即待停车车辆行驶的通道，方向定位从左向右。将通道上判断是否可以驶入临时存放区的那一格称作“等待格”，即图中▲处，临时存放区中的每一个存放区域称作“中转房间”，即图中★处，此处以三个中转房间为例。等待格及其左边的三格是等待区中较为特殊的区域，即B 到A 之间的区域。当车辆在等待格左边三格时，若前方畅通，则继续向前行驶，更新位置不超过等待格；若前方已经出现了排队拥堵，则等待直至前方畅通。当车辆到达等待格时，判断AGV 泊位是否已经停满，若泊位已满，则车辆在等待格等待，后续车辆也依次排队等待；若泊位未满，车辆驶入空的临时存放区。若临时存放区内有多处中转房间为空，为减少临时存放区的冲突，车辆优先进入近端的临时中转房间。

图1 AGV 停车区车辆行驶模型示意图

1.2.2 临时存放区存取车模型

车辆的存放流程如图2（a） 所示。车辆到达等待格后，判断AGV 泊位是否已满。若AGV 泊位已经停满，则只有出库车辆可以进入中转房间，入库车辆只能在等待格等候；若AGV 泊位尚未停满，则判断中转房间是否为空。若中转房间为空，入库车辆则从等待格驶入中转房间，停留45 秒后，进入内部操作区域；若中转房间不为空，入库车辆则继续在等待格等待，直到可以进入中转房间。

车辆的提取流程如图2（b） 所示。在AGV 内部停车的车辆，判断是否停车结束，需要取车。若需要取车，则判断中转房间是否为空。若中转房间为空，车辆则占用中转房间；若此时中转房间已被占据，则继续等待中转房间空闲。车辆在中转房间内会停留60 秒，供驾驶员进入车内启动车辆等。直到驾驶员完成取车动作，才会继续判断前方通道是否畅通。若前方通道不畅通，车辆仍然保持对中转房间的占用，直到前方通道畅通后，车辆驶出中转房间。车辆驶出中转房间后，就回到了外部通道上，继续遵循通道行驶模型的通行规则。

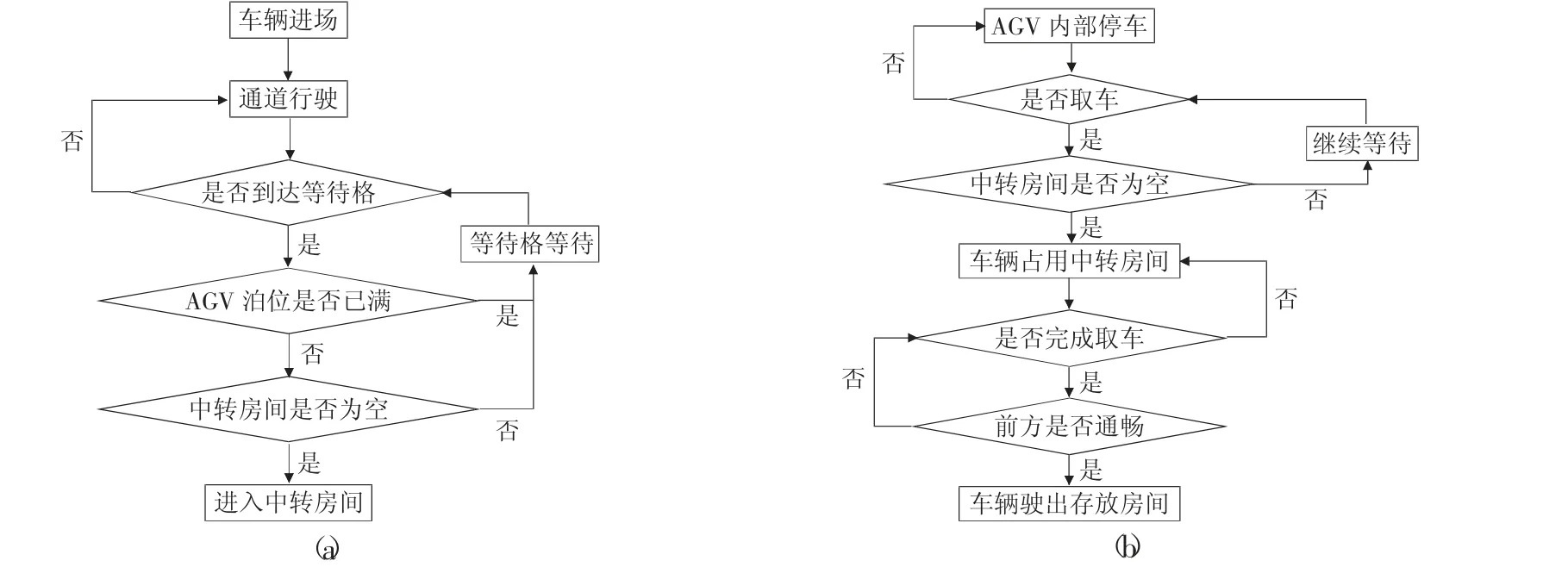
图2 临时存放区存车（a）、取车（b） 流程图

2 AGV 停车库运行仿真及评价指标

2.1 AGV 停车库运行仿真

本文依据某实际城市商业综合体的地下停车场进行模拟仿真，该地下停车场总共有492 个车位，2 个具有双向进出功能的进出口。其中，AGV 停车区原先布置传统停车位48 个，经过改造后车位数量增加约30%达到63 个，采用Matlab 建立AGV 停车库模型如图3 所示。在模型中，单个元胞的尺寸为3m×3m，系统的时间步长为1 秒，车辆最大速度为15km/h，最大加速度为3m/s，车辆在车位的停靠时长为60～120 分钟。

图3 AGV 停车库模型布局示意图

车辆进场后，在通道内行驶到等待格，经由临时存放区后进入内部操作区，出场车辆在停车时间结束后，经由临时存放区到达外部通道。由于车辆必须要经过临时存放区才能进出AGV 停车区，而车辆存、取车时又会占用临时存放区，因此临时存放区是影响AGV 停车模式停车效率的关键。若临时存放区的中转房间过少，则会出现大量车辆等待排队、存取车辆矛盾突出的情况；若临时存放区的中转房间过多，又会占用过多的地下停车场面积，造成资源浪费。针对该AGV 停车区，本文设置了1-5 个中转房间的方案，其运行效果分别如图4 所示：

图4 AGV 停车库运行仿真效果图

2.2 AGV 停车库运行效果评价指标

（1） 车辆平均延误。车辆的平均延误分为平均进场延误和平均出场延误，指的是平均每辆车从进场到停车、从取车到出场过程中的延误时间。在本文的AGV 停车库仿真中，车辆的延误包括通道运行排队延误、临时存放区等待延误。

（2） 最大排队长度。最大排队长度指的是在运行过程中出现有车辆进行排队时队列中最后一辆车车尾距第一辆车车头之间的距离，以m 为单位。在本文中，AGV 停车库运行过程中的最大排队长度用l表示。

（3） 临时中转房间占用时间。当临时存放区有多个中转房间时，中转房间被占用的时间反映了该房间的被使用情况。在进出场车辆总数一定的情况下，临时存放区的总占用时间基本不变，因而不同中转房间的被占用时间，也能够表示该房间的利用率。

3 AGV 停车库运行效果

由于模型中车辆的通行、停放时间等参数服从正态分布，因此，模型单次的运行结果具有随机性。为降低随机效应对运行效果的影响，本文对每种方案进行了100 次仿真运行，每次仿真时间20 000s，各评估指标采用100 次运行结果的均值和标准差表示。

3.1 极限运行状态

根据现有停车场的进场效率，每辆车平均耗时10s，因而在极限状态下，整个地下停车场两个进口道的总进场速率为720pcu/h。进入AGV 停车区的速率则根据停车场流线及车位数比例进行随机分配，当AGV 停车区剩余车位为0 时，则系统暂停向AGV 停车区分派车辆，直到AGV 停车区出现空车位。

极限运行状态下各中转房间方案的平均进场延误时间如图5 所示，从图中可以看出，只有1 个中转房间时，平均进场延误时间大于1 000s，而中转房间个数为2 时，平均进场延误时间显著减小到约550s；随着中转房间个数的增加，平均进场延误时间继续减小，但降幅相对较小，有5 个中转房间时，平均进场延误约为510s。

图5 极限运行状态下各中转房间方案平均进场延误

极限运行状态下各中转房间方案的平均出场延误如表1 所示，当中转房间个数为1 时，平均出场延误约为375.77s（标准差93.05s），而当中转房间为2 个时，平均出场延误时间显著减小至13.74s（标准差8.22s）；随着中转房间数量的增加，出场延误时间继续减小，有5 个中转房间时平均出场延误降为0。

表1 极限运行状态下各中转房间方案平均出场延误

极限运行状态下各中转房间方案的最大排队长度如图6（a） 所示，随着中转房间个数的增加，最大排队长度依次减小。图6（b） 展示的是极限运行状态下各中转房间的被占用时间，由于本文设定每辆车存车和取车时占用中转房间的时间是相同的，进出场车辆数量也是相同的，因而五种不同方案下，中转房间的总占用时间是相同的。但从图中可以看出，左右两端的房间（即最左侧房间和最右侧房间） 的占用率要明显高于中间区域的房间，这与模型的算法设置有关，即出场车辆优先从最右边中转房间取车，进场车辆优先从最左边中转房间存车，以减少中转房间正对区域的交通冲突。

图6 极限运行状态下各中转房间方案(a) 最大排队长度及(b) 被占用时间

极限运行状态下各中转房间占用时间比例如表2 所示。只有1 个中转房间时，所有车辆都占用①号中转房间，因此，其占用比例为100%；有2 个中转房间时，两个中转房间被占用的时长较为平均，①号占用56%，②号占用44%。随着中转房间继续增加，各中转房间被占用时长的比例持续减小，最大占用时间比例小于40%。

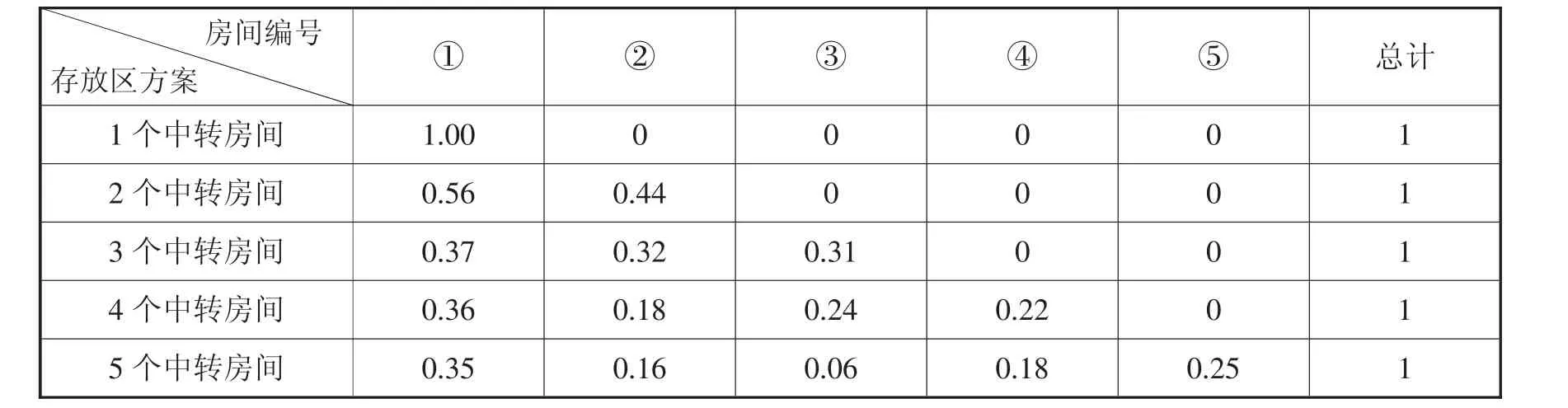
表2 极限运行状态下各中转房间占用时间比例

3.2 高峰期运行状态

城市商业综合体地下停车场的统计结果表明，高峰期的进场小时流量约为停车位总数的40%～50%。因此，在高峰期运行状态下，设置整个地下停车场的总进场速率为240pcu/h，并根据停车场流线及车位数比例分配AGV 停车区的进入速率。

在高峰期运行状态下，各中转房间方案的平均进场延误和平均出场延误分别如表3 和表4 所示。可以看出，只有1 个中转房间时的平均进场延误和平均出场延误均远大于其他方案。当有2 个中转房间时，平均进场延误为1.41s，平均出场延误为3.71s，远小于1 个中转房间的情况，而与大于等于3 个中转房间的情况相差不大。

表3 高峰期运行状态下各中转房间方案平均进场延误

表4 高峰期运行状态下各中转房间方案平均出场延误

在高峰期运行状态下，各中转房间方案的最大排队长度和被占用时间如图7 所示。从图7 (a) 中可以看出，当中转房间数量大于等于2 个时，AGV 停车区的最大排队长度基本一致，远小于1 个中转房间的情况。从图7 (b) 中可以看出，当中转房间个数大于等于3 个时，位于中间的中转房间利用率已经远小于两侧的中转房间。中转房间被占用时间比例如表5 所示，可以得知，有3 个中转房间时，②号房间占用比例仅为14%，明显小于两侧房间的占用比例。且随着中转房间数量的增加，两侧中转房间的占用比例均在40%左右，中间房间的利用比例较低，造成空间的闲置浪费。

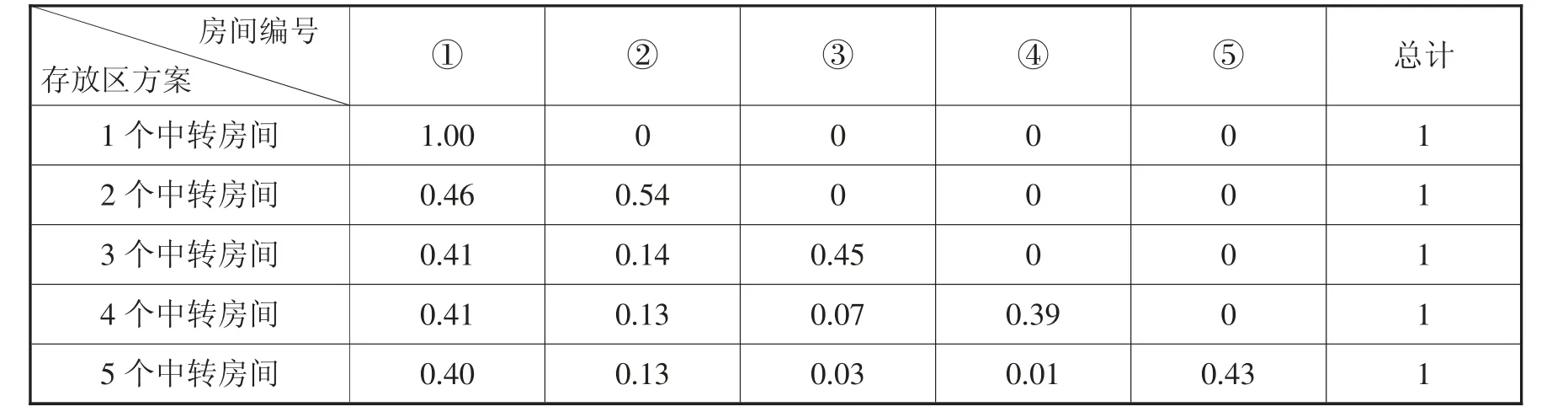
表5 高峰期运行状态下各中转房间方案中转房间被占用时间比例

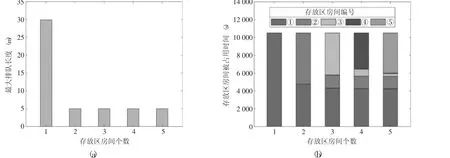
图7 高峰期运行状态下各中转房间方案最大排队长度比较

4 结 论

针对AGV 停车库临时存放区的合理设置及效果评估，本文建立了AGV 停车库CA 仿真模型，对5 种临时存放区设置方案进行了运行仿真研究，采用车辆平均延误、最大排队长度和中转房间被占用时间评估了各方案在极限状态和高峰期状态的运行效果。研究结果显示，本文提出的CA 仿真模型能够用于AGV 停车库临时存放区设置方案的效果评估，调整相关参数即可用于具体的AGV 停车库临时存放区的优化设计；针对本文分析依托的实际案例仿真结果表明，在极限状态和高峰期状态下，2个中转房间即可满足配有63 个车位的AGV 停车库的运行需求，是最合适的临时存放区设置方式，而过多的中转房间会导致空间资源的浪费。