基于改进遗传算法的网约车共乘优化调度模型求解

胡 凯，袁鹏程，胡忠恺 Hu Kai, YUAN Pengcheng, HU Zhongkai

（上海理工大学 管理学院，上海 200093）

0 引 言

网约车共乘优化调度模型（DARP-M） 是近些年来在交通领域上逐渐兴起的一类调度模型，属于带能力约束的车辆路径优化问题（Capacitated Vehicle Routing Problem, CVRP），它直接影响车辆总行驶距离和最大满载条件下的车辆使用数量。随着互联网的高速发展以及当下疫情现状，DARP-M 模型在公共交通领域得到了广泛应用，具有重要的理论以及实际应用价值。

车辆路径问题（Vehicle Routing Problem, VRP） 是一个典型的NP-hard 问题，而本文中提出的网约车共乘优化模型是在这个问题的基础上增加了车辆载重约束以及车辆路径约束，因此在路径优化的过程需要综合考虑车辆数量、乘客分配、路径选择等因素，使得运行总费用最少。但是在具体求解的过程中，通常会存在一些问题：约束限制了优化对象新解的生成，会降低算法的全局搜索能力，且传统遗传算法极易陷入局部最优解，随着约束的增加，这一影响愈加明显。其次，针对约束与DARP-M模型的融合，算法很难在结构、复杂度、精度上做出整体的简单高效。基于上述问题，众多学者从合乘问题以及构建高效解决多约束车辆路径问题的算法这两个方面进行入手展开研究。

1 相关研究

目前合乘问题已得到国内外学者的广泛关注并取得了丰富的成果。在如何求解网约车合乘模型的过程中，研究的主要目标是达到最优化的运营成本。优化原本的运营方式就是在满足乘客需求的同时，尽可能的最小化路程或成本。陈久梅等提出变邻域搜索算法来解决开放式带时间窗车辆路径问题。Firat、Goekay讨论了在最大等待时间和最大乘坐时间约束下的合乘问题的可行性测试。符卓等针对带软时间窗的需求依订单拆分车辆路径问题及其优化算法进行研究，建立了问题的数学模型，设计了求解的禁忌搜索算法。范厚明等针对带模糊需求与模糊时间窗的车辆路径问题，为提高种群的多样性，改进了交叉算子，在引入局部优化算法及擂台法则的基础上，设计了适合求解多目标车辆路径问题的混合遗传算法。Hame设计了超链接诱导主题搜索（HITS），根据枢纽分数对节点进行排名，并为回溯算法提供了指导，该算法可以有效地找到合乘问题的可行解决方案。王超为求解带时间窗和同时取送货的车辆路径问题（VRPSPDTW），提出一种离散布谷鸟（DCS） 算法。覃运梅在综合考虑了司机和乘客双方利益的基础上，以车辆行驶路程作为优化目标，建立了出租车合乘模型。在求解算法方面，Huang Yan提出了一个动态树算法，相比于分枝定界算法和整数规划算法能够更好地调度动态请求和动态路径调整，并结合了上海的出租车真实数据进行实验验证。Hosni 等将共享出租车匹配问题和出租车最优路径计算问题作为一个混合整数规划来处理，结合拉格朗日法进行求解，并提出了两种启发式算法来获得高质量的可行解。Quo, Jingmei 等提出了一种基于时间依赖性的启发式算法,来保证给定的取货和交货顺序是否存在可行。潘雯雯等以多车型和需求拆分阈值为新约束，建立需求可拆分的多车型车辆路径问题（SDHFVRP） 混合整数规划模型；提出以路径优化和路径改进相结合的两阶段算法（TPA）。马傲雯等提出采用时间组替代传统的距离匹配，采用A 星搜索算法完成车辆的实时订单顺序，并确定该订单的划分车辆。Nourinejad 等提出了一种基于分布式拼车系统的匹配算法来解决多乘客和多司机的配对问题，并提高了共享出行中司机和乘客的匹配成功率。Masoud 等提出了一种实时优化的乘车匹配算法，在最大化系统中服务的乘客数量的同时，通过考虑用户对出行需求的偏好以及最小化换乘次数和乘客等待时间，使出行尽可能舒适。Parragh 等在考虑合乘问题时，提出了一种混合列生成和大邻域搜索算法，并考虑时间窗口等限制，使总路径成本最小化。熊浩等针对可拆分车辆路径问题（SDVRP），其求解方法与需求不可拆分的VRP 问题有较大的区别，本文提供了一种新的求解思路——基于双层规划模型的三阶段禁忌算法。揭婉晨等研究含时间窗的多车型电动汽车车辆路径问题，建立了一个混合整数规划模型，并利用分支定价算法求其最优解。穆东等为提高传统串行模拟退火算法求解时间依赖型车辆路径问题的效率，提出一种并行模拟退火算法。颜瑞等研究包含时间窗、多车场因素的二维装箱车辆路径问题，建立相应的数学模型，并提出求解该问题的一种新的混合算法，混合算法由量子粒子群算法和引导式局部搜索算法组成。针对带时间窗车辆路径问题（VRPTW），提出了混合种群增量学习算法（HPBIL），用于同时最小化车辆数和总行驶距离。

通过引入不同场景下的约束，基本的车辆路径问题能扩展出大量不同的衍生问题，而基础的求解框架与优化方法会直接影响算法的构建难度与求解效果，因此，基于传统算法改进出通用性强且易于数据耦合的优化方法具有相当重要的意义。

基于上述情况，为高效求解DARP-M 问题，本文提出一种结构简单、通用性较强的多路径优化方法，并且针对不同车辆的运载能力约束以及路径约束提出一种带有较强敛优属性的改进遗传算法（Improved Genetic Algorithm，IGA），结构上基于遗传算法（Genetic Algorithm，GA） 的整体框架，为了提高算法的全局搜索能力，依次设计了初始可行解的生成、较优解的接收、灵活的交叉变异策略，详细地解析了IGA 算法的运算过程以及优化原理，然后通过对不同算例进行对比试验，验证了此类算法的有效性和鲁棒性。

2 DARP-M 的数学模型

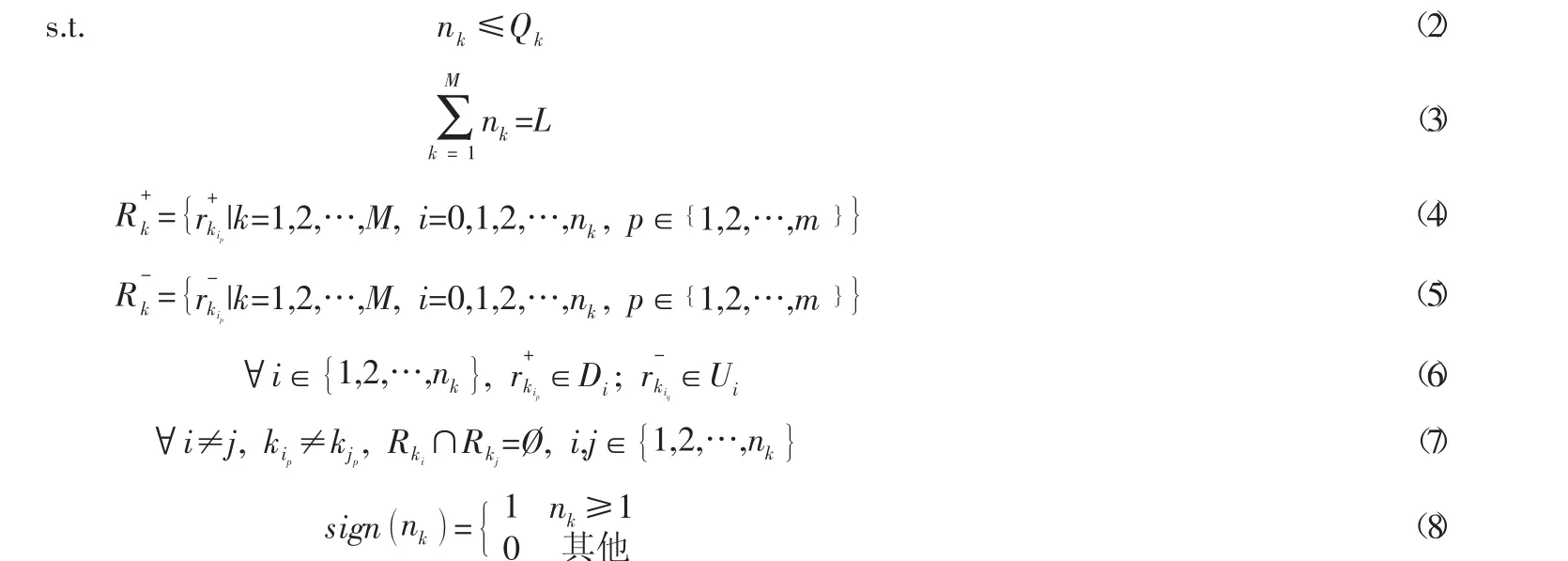
其中：式（1） 为DARP-M 的总求解目标，即车辆服务的总成本最少；式（2） 表示每辆车上的乘客不能超过车辆容量限制；式（3） 表示每位乘客都需要得到配送服务；式（4） 表示每条上车路径的客户组成；式（5） 表示每条下车路径的客户组成；式（6） 表示上下点必须保证在指定范围内；式（7） 限制每位乘客只能由一个配送车辆完成任务；式（8） 表示如果是第k辆车参与了接送服务，则sign n()=1，否则sign n()=0。

DARP-M 场景如图1 所示：

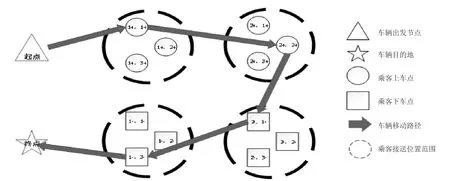
图1 DARP-M 场景图

3 IGA 算法的设计与实现

本章从算法框架、生成初始可行解、交叉变异操作以及较优解的筛选这四个方面进行阐述，重点设计了结构清晰且各个功能模块相对独立的DARP-M 模型框架，在原有的遗传算法的基础上，提出了针对多约束模型的IGA 算法。

3.1 基于多约束条件的遗传算法框架

DARP 作为VRP 所衍生的一类车辆调度问题，更符合当下实际需求，DARP-M 模型也是DARP 的衍生模型，而构建较好的算法求解框架，是高效求解此类问题的关键。遗传算法因其使用广泛且结构简单而被较多应用于求解多约束耦合问题。因此，本文结合相关路径优化特征，来构建基于遗传算法的DARP-M 问题求解框架。如图2 所示，本文所涉及的GA 算法框架大致分为三步，首先是得出符合限制条件的车辆与乘客的分配方式（GM Operation），根据求得的分配方式得到初始可行解（FDF Operation）。结合具体的遗传算法操作，生成的初始可行解和邻域结构的变换是在考虑约束满足的条件下来产生新解（GA Operation），较优解的筛选就是以可行解的数值优化为目标，在新解加入后不断进行迭代选优。框架的核心思想就是将生成满足约束的可行解与目标优化相隔开，各个模块的功能明确且相互独立，便于程序的设计和更改。在面对不同问题时，只需要根据模型特征对初始解的生成进行更改，对交叉变异操作及更优解的选取进行改进即可。

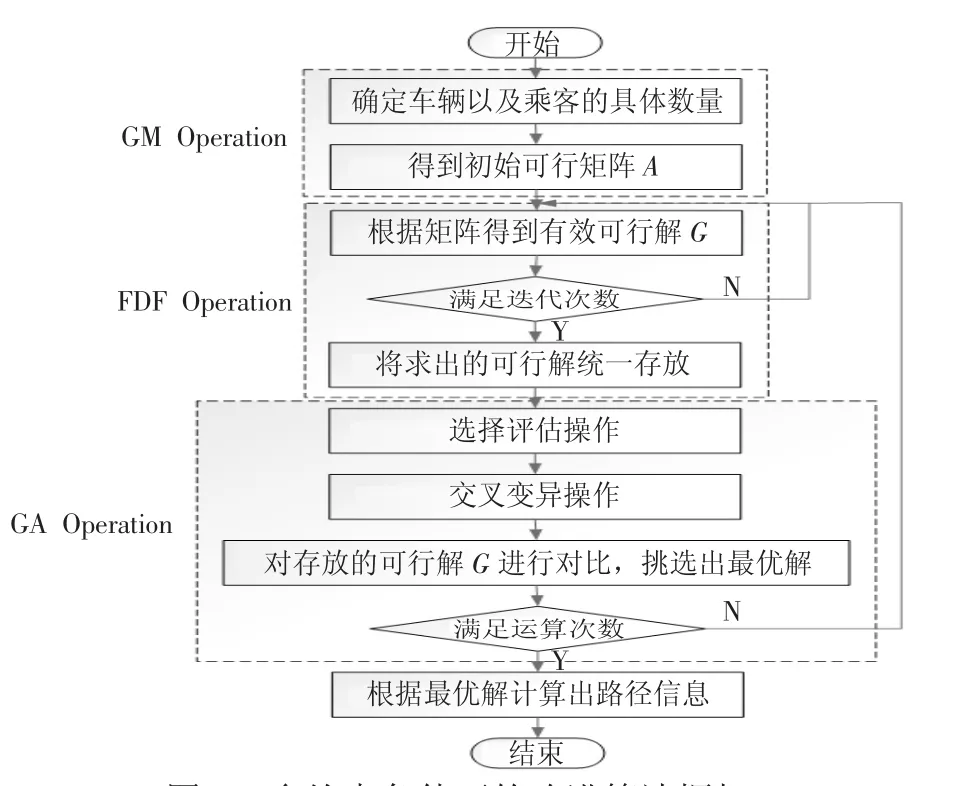
图2 多约束条件下的改进算法框架

3.2 生成初始可行矩阵（GM Operation: Generate Initial Feasible Matrix）

矩阵中每一行之和不能超过车辆容量的限制，且矩阵的每一列之和必须等于1，表示一位乘客只能选择一辆车，中途不得上下车。

3.3 求出可行的行驶费用（FDF Operation:Find out feasible Driving Fee）

3.4 遗传算法（GA Operation：Genetic Algorithm）

在上一步中通过循环得到初始可行解，这里用传统遗传算法的步骤对初始可行解进行选择评估、交叉、变异等操作，并且将之前迭代的最优解放入变异操作后的矩阵中，形成一个新的矩阵A。算法中的选择评估操作即将原本劣等解的位置替换为优质解，从而达到改进整个种群的目的，交叉以及变异过程见后几节。算法的伪代码如下：

（1） 设置程序迭代次数NP；适应值Fit；行程费用G；费用最大值maxG; 费用最小值minG;

（2） 前面的运算中已经求得了一个费用，记为G；

（3） Fit=1- (G-minG )/ (maxG-minG )；

（4） For i=1∶NP；

（5） 对矩阵A 进行选择评估操作生成新矩阵nf；

（6） EndFor；

（7） For j=1:NP；

（8） 对矩阵nf 进行交换、变异操作生成新矩阵A；

（9） If 未达到运算次数；

（10） 执行FDF Operation；

（11） 根据A求得一个新的最小费用，记为G；

（12） If G≤G；

（13） 最小费用不变；

（14） Else；

（15） 将最小费用改为G；

（16） EndIf；

（17） Else；

（18） 计算出路径信息；

（19） EndFor。

3.5 交叉操作（Overlapping Operation）

将矩阵nf 中两连续的子矩阵提取出来，如果两子矩阵完全相同，则无需进行交叉操作，反之，则将两个矩阵分别表示成数组编码的形式，将各个乘客位置用数字表示出来，按车辆顺序排列。

交叉操作遗传操作中起着至关重要的作用，它可以提高各个有效解之间的差异度，以便于快速收敛，考虑是在整数编码的操作环境下，本文使用的是两种交叉操作方式：单点交叉和两点交叉。对于这两种交叉方式的选择，设置交叉率为θ，并且随机生成[0,1 ]之间的随机数δ，如果θ≤δ，则使用单点交叉，反之，则使用两点交叉。单点交叉操作如图3 所示，两点交叉操作如图4 所示。

图3 单点交叉操作

图4 两点交叉操作

3.5.1 单点交叉操作

首先是给定两组编码parent、parent，在一行编码的任意位置随机选择一个交叉点（箭头所指位置），交换两行编码在交叉点后的元素，若一行编码中存在两个相同的序号，那么在另一行编码中选择相同位置的序号，两两彼此进行交换，重复此步骤，直到无重复序号，得到子代编码child与child。

3.5.2 两点交叉操作

首先是给定两组编码parent、parent，在一行编码的任意位置随机选择两个交叉点（箭头所指位置），交换两行编码中在两交叉点之间的元素，若一行编码中存在两个相同的序号，那么在另一行编码中选择相同位置的序号，两两彼此进行交换，重复此步骤，直到无重复序号，得到子代编码child与child。

3.6 变异操作（Mutation Operation）

变异操作是指在编码中随机引入突变来增加种群的多样性，消除算法在无希望地区的停滞，探索新搜索区域的过程。变异率为λ，当随机数δ≤λ 时，对数组进行变异操作。本章介绍的变异操作也有两种，分别是局部变异和整体变异。局部变异是以不改变车辆搭载乘客的数量下进行的，只有在局部变异无效后，才会使用整体变异。局部变异流程如图5 所示，整体变异流程如图6 所示。

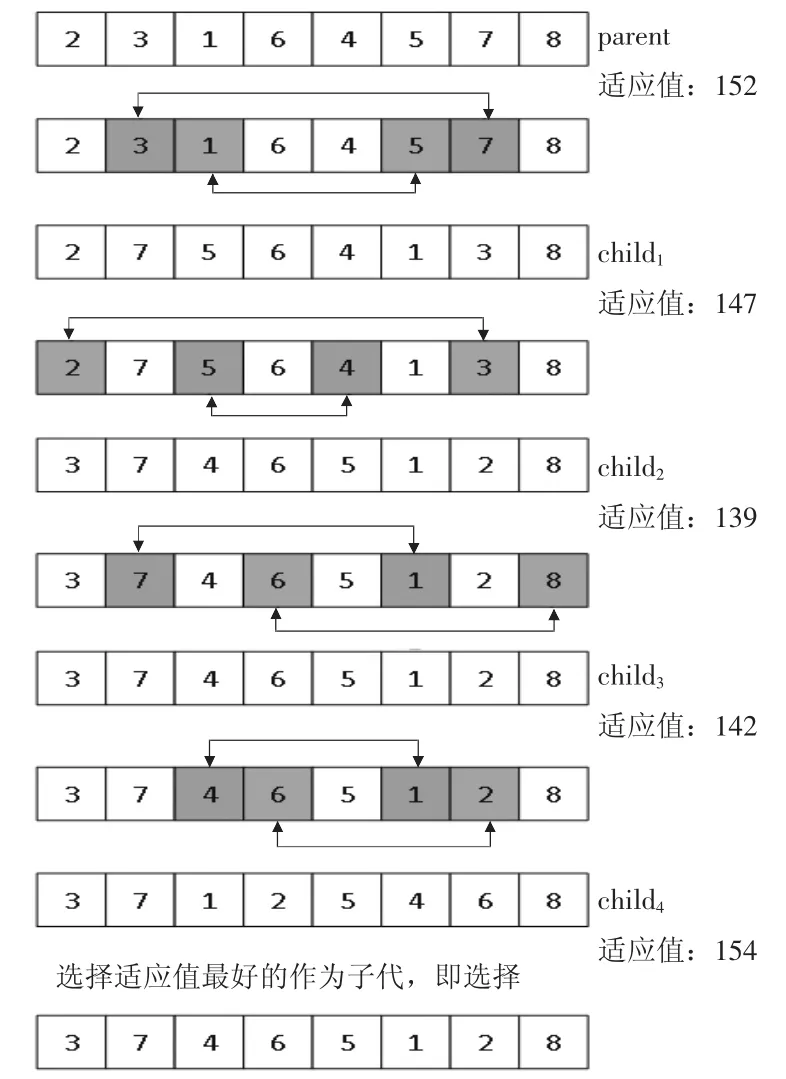
图5 局部变异流程图

图6 整体变异流程图

3.6.1 局部变异操作

局部变异即将数组中任意抽出四个数字作为两组进行两两交换。但是在进行变异的过程中，还应注意保护优质解，由于变异的特性，之前可能求得的优质解，会在经过变异后丢失。针对这一情况，选择在每一次变异后对编码进行还原，计算适应值，设置具体的突变次数，将适应度最好的保留下来进行下一次的运算。如图5 所示，突变次数设为4 次。

3.6.2 整体变异操作

在执行变异操作时，会出现在突变次数内无法收敛的情况，这时就需要改变每位辆车搭乘乘客的数量。如图6 所示，父代编码用三种颜色来表明乘客搭乘的情况。图例中二号和三号乘客乘坐第一辆车，一号和六号乘客乘坐第二辆车，其余四位乘客搭乘第三辆车，通过不断改变乘客乘坐车辆的信息来达到变异的目的，在每一次变异后对编码进行还原，计算适应值，突变次数与上文一致，将适应度最好的保留下来进行下一次的运算，如果整体变异后子代仍然无法优于父代，或数值上等于父代，则结束变异，保留父代进入下一次的运算。

3.7 还原操作（Restore Operation）

图7 部分变异后的还原操作

在部分变异操作无效后，需要整体变异来达到收敛效果，但整体变异打乱了车辆搭乘乘客的数量，因此，整体变异后的矩阵还原是按照乘客被分配的车辆来进行还原。图8 表示的是经过整体变异后矩阵还原的过程。

图8 整体变异后的还原操作

4 算例分析

4.1 算例描述

假设存在两个位置节点，分别作为提供合乘服务车辆的起点和终点，可提供服务的车辆有3 辆，其中2 辆是容量为3 人的出租车，一辆是容量为5 人的桥车，同时向8 位乘客提供共乘服务，并且这8 位乘客有3 个与可能的接送位置相对应。配送中心位置、乘客数量、乘客可能的接送位置等数据参考DARP 相关文献。配送中心坐标分别为(0,0 )和(20,20 )，而客户可能的接送位置坐标都是随机且独立的分布在[0,2 0 ]× [0,2 0 ]的矩形区域中。不同车辆的成本在上文已经提到，这里a取12，a取8，h取0.7 元/公里，h取1.05 元/公里，各个节点的位置坐标如表1 所示：

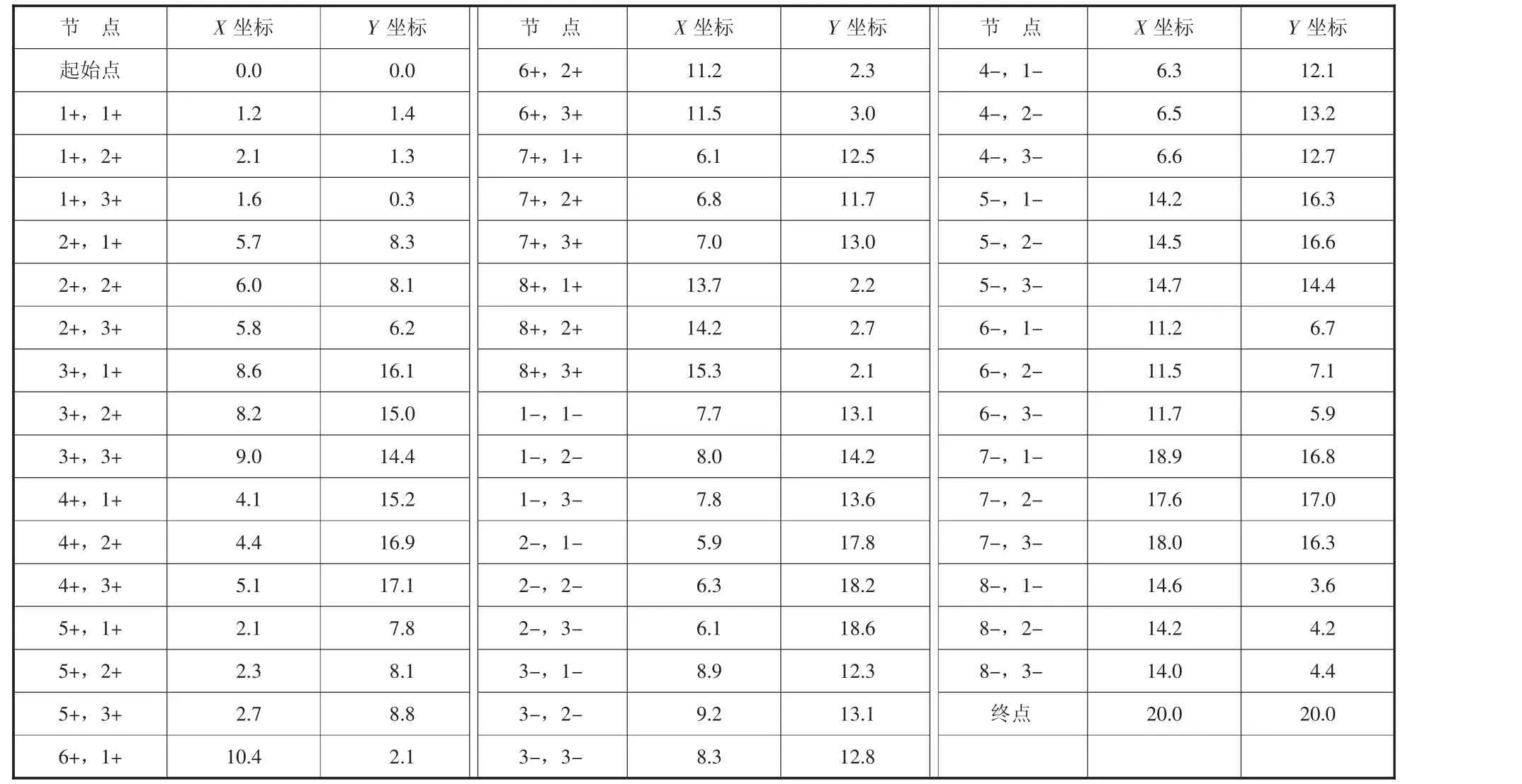
表1 各节点位置坐标

4.2 算法参数的灵敏度分析

算法参数的合理设置对算法的有效性和计算效率有相当重要的影响，本文中涉及到的参数：迭代次数、种群规模（Group Scale, GS）、交叉率、变异率以及不同参数相互组合的结果。此外，还有新加入的参数：平均运行时间（Average Running Time，ART）、运算结果平均值（Average Operation Result，AOR）、最优值（Bes）t、迭代次数（Iters）、结果与最优值的偏移度（Deviation Degree，DDE），DDE=(AOR-Best )/Best )*100%。

4.2.1 迭代次数（Iters）

迭代次数在算法中起到至关重要的作用，迭代次数过高会延长算法的运行时间，而迭代次数过低就会提前结束搜索结果,首先经过多次使用程序计算得出最优值，而后通过改变迭代次数独立运算10 次，取得平均运算时间和平均运算结果,涉及到的参数：种群规模为20，交叉率0.8，变异率0.5，运算结果见表2，由表2 可以得出迭代次数与运算结果的平均值是呈现正比的关系，一般来说，在程序运行到20～30 次之内，就基本上已经达到最优值或者趋近于最优值，但随着迭代次数的增加，平均运行时间也随之大幅增加，由最后的结果可知，算例在30 次迭代之内都接近得到最优解，因此，本文设置迭代次数Iters=30。

表2 不同迭代次数下的运行结果

4.2.2 种群规模（Group Scale, GS）

设置种群规模，同样取上述几个参数值进行测试，表3 中给出了在不同的种群规模下，对算例进行独立10 次运行的平均计算结果，迭代次数设为10，交叉率0.8，变异率0.5。由表3 可知，随着种群规模的增大，运行结果也不断趋于最优，但优化速度越来越慢，且运行时间大幅增加，考虑到解的质量和运行时间，本文中种群规模取20。

表3 不同种群规模下的运行结果

4.2.3 交叉率与变异率

交叉率数值的大小用于决定交叉操作是单点交叉还是两点交叉，这对于是否能够保留亲本特征是比较重要的。变异是遗传算法的主要步骤之一，本文中的部分变异操作能够筛选出局部最优解的情况，而整体变异则能够跳出局部最优，以不同方向来寻找最优解。本节通过设置了若干个不同的交叉率以及变异率，表4 是对算例在不同情况下运行10 次的平均测试结果，迭代次数为20，种群规模为10。由测试的运行时间与DDE 值可以看出，变异率与运行时间呈正相关，与偏移度呈负相关，当交叉率为0.8，变异率为0.5 时，算法的求解时间与解的质量较优。

表4 不同交叉变异率下的运行结果

4.3 算例优化结果

通过上述改进的遗传算法以及参数设置，对案例进行求解分析。实验环境为lntel（R） Core（TM） i5-6300HQ CPU@2.30GHz，操作系统为64 位Windows10，使用Matlab R2016a 进行编程。运算中迭代次数（Iters） 为30，种群规模为20，交叉率为0.8，变异率为0.5，运行时间为105.152s。基于发出合乘请求的节点数据和提供服务的车辆数据等要求，求解本文构建的DARP-M 模型，得出最优合乘路径有3 条如表5 所示。车辆的总运输成本为128.794 元，包括三辆车的固定费用28 元。具体的路线图以及适应度进化曲线图如图9 及图10 所示。

表5 具体的行驶路线情况

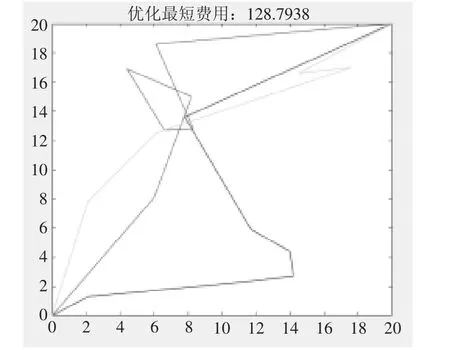
图9 行驶路线图

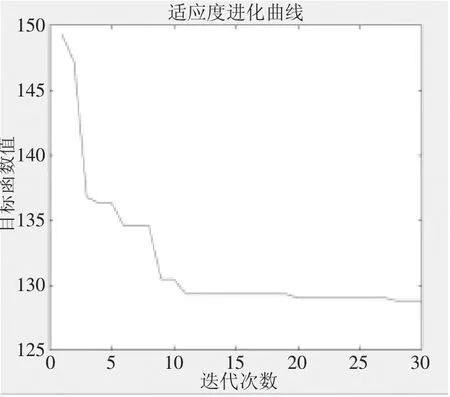
图10 适应度进化曲线

5 总 结

国内外新冠肺炎病毒（COVID-19） 的爆发，对城市居民的日常生活造成了严重影响。在如今后疫情时代的大背景下，基于车辆路径问题，提出了所要研究的DARP-M 模型，本文针对这一模型提出了IGA 算法，并综合考虑了网约车车辆的运输成本、车辆固定成本、路径限制等。利用Matlab 编程对算例求解，可为疫情下的合乘车辆路径优化提供理论依据。基于本文所依据的背景是后疫情时代，对于乘客的要求没有考虑在内，每位乘客的允许等待时间都是不一致的，车辆必须要在要求的时间范围内接送乘客，此外，司机以及乘客的健康状况没有考虑在其中，在实际的情况下，乘客在体温过高时，就不适宜再进行合乘服务了，需要额外分配的车辆进行接送，这个可以考虑作为下一步的研究方向。