基于疫情需求的A 医药公司抗疫物资配送研究

曾 锐，黄钰婷，沈 凯,2 ZENG Rui, HUANG Yuting, SHEN Kai,2

（1. 广东药科大学 医药商学院，广东 中山 528400；2. 广东省药品监管科学研究基地，广东 中山 528400）

0 引 言

新冠疫情是百年来在全球范围内发生最严重的流行传染病之一，危害人民生命安全，影响社会经济运作。而随着国内形势总体稳定，境外疫情防控依旧严峻，我国进入了疫情防控常态化时期，疫情时有反弹。常态化防控对抗疫物资配送时效要求较高，不同类型的需求点对配送时效提出不同的要求，医药流通企业在肩负抗疫物资配送使命的同时需兼顾运营成本，对企业抗疫物资配送提出了新的要求和考验。近些年来，应急物资配送成为了学术界研究的热点。苏兵等针对应急救援物资供不应求的情形，建立以单个需求点最大缺货量最小为目标的单个配送中心、车辆有限和带时间窗的配送路径模型并进行求解。梁永梅等在配送路径最短的基础上，考虑了人均配售时间，以最短路径和最多人均可利用配售时间两方面构建应急医疗物资配送模型，并利用遗传算法求解。黄辉等则结合了车辆分配公平性和配送及时性，建立基于军民合作“分配—运输”集成决策模型。朱佳翔等研究了“灰不确定性”与“鲁棒不确定性”对应急物流配送的影响，基于灰色动态优化模型进一步提出了鲁棒H∞控制策略。陈宇丹则以配送时间最短与受灾点满意度最大为目标，构建双目标应急医药物流配送车辆调度模型。而本文则兼顾A 医药公司的配送时效和企业效益，针对社康中心和医院的抗疫物资配送进行研究。提出设立3 个临时储存点，通过指数平滑法预测需求，并以社康中心和医院对抗疫物资配送时效的不同要求为约束构建软、硬时间窗VRPTW 模型，以模拟退火算法进行求解得出配送路径。

1 社康中心、医院配送设计

A 医药公司是一家医药流通企业，仓库位于广州市越秀区，主要为珠三角的社康中心和医院提供医疗药械的仓储和配送服务。当接收到药械订单后，将药械从广州仓库配送到各需求点。疫情使社康中心和医院的药械消耗增大，出于疫情防控的需要，A 医药公司需以更快的速度向社康中心和医院配送药械，保障用药需求，但广州仓库到部分需求点距离较远，配送时间长，难以满足防疫要求。

为缩短配送时间，A 医药公司拟定租赁1～4 个更接近各服务对象的临时储存点（位于珠三角的中山、东莞、深圳、珠海等地），并规划更合理高效的配送路径。供应商越库配送，提前将部分抗疫药械送往临时储存点暂存，当接收社康中心和医院的订单后公司直接将暂存的抗疫物资按照规划好的配送路径运往各需求点。

1.1 临时储存点的选址

多重心法是一种可用于选取仓库位置的方法。将配送点按照一定的原则进行分组，再通过考虑每个群组配送点间的距离和配送的货物量，将仓库尽可能接近运量较大的配送点，从而使运量较大的配送点可以获得一个相对较短的路程，进而提高配送效率，降低配送成本，提高服务水平。

本文将利用多重心法选取租赁的临时储存点。先将需求点的经纬度转化成高斯—克吕格平面直角坐标系的坐标位置。与A 医药公司有业务往来的36 个社康中心和15 个医院的平面坐标位置和平均需求如表1 所示：

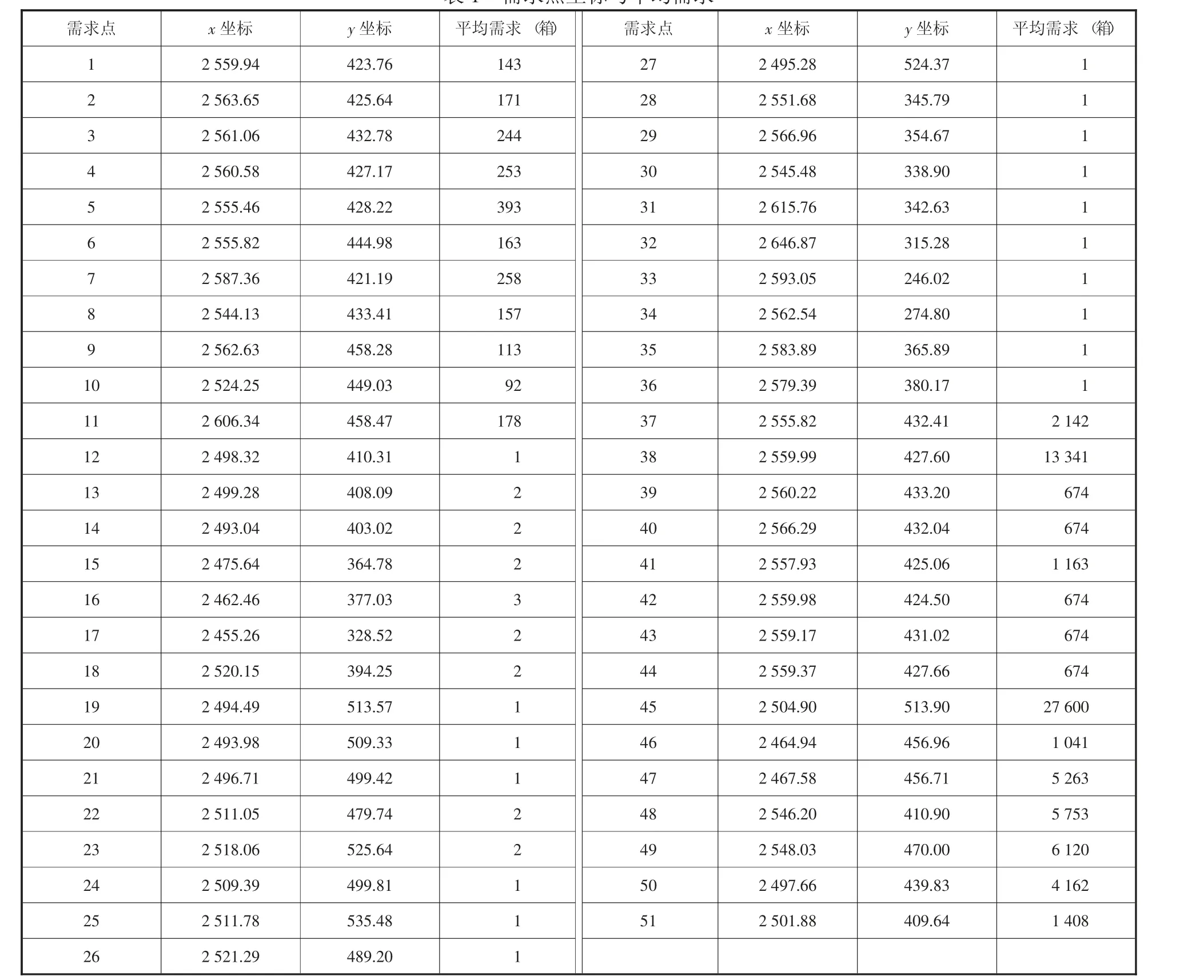
表1 需求点坐标与平均需求

A 医药公司拟定租赁1～4 个临时储存点，因此本文利用logware 软件中基于多重心模型思想的“MULTICOG”模块求解临时储存点的位置，设计出四套选址方案。选址方案如表2 所示。

表2 多重心选址求解结果

本文以运输成本、租赁成本、管理成本三个维度来计算选址方案的总成本，总成本最低的为最优方案。其中，运输成本=各临时储存点的配送距离*配送车辆数；租赁成本=各临时储存点的单位月平均租金*租赁面积；管理成本=各临时储存点所在地市的平均薪资水平*员工数。对各方案的成本进行计算，结果如表3 所示。

表3 各方案成本比较

C＜C＜C＜C，因此方案3 为最优方案，即设立3 个临时储存点，其坐标位置分别为（2 548.03,470.00）、（2 559.99,427.60）和（2 504.90,513.90）。

1.2 预测需求量

分析A 医药公司的历史销售数据，利用指数平滑法预测有业务往来的社康中心和医院在2021 年4 月的需求以确定配送量，需求预测结果如表4 所示：

表4 2021 年4 月需求预测结果

1.3 配送路径设计

1.3.1 参数设置与说明

1.3.2 社康中心路径设计

（1）构建VRPTW 软时间窗模型

在疫情防控背景下，社康中心对抗疫物资的需求比医院小，主要涉及轻症、普通型病例治疗药品，重要程度和时效的要求相对较低。但其配送点零散且数量较多，对配送的路径设计方案提出了较高的要求。社康中心全天均可接收抗疫物资，要求车辆出发后12 小时内到达社康中心。对此，本文在普通的车辆路径问题基础上加入时间限制，即允许最晚到达时间LT 为12。若超时到达则会面临时间成本的惩罚，1 分钟惩罚值为5 元（即迟到1 小时惩罚300 元），因此时间惩罚系数γ 为300。构建带有时间惩罚的配送成本目标函数，求其最优解，将其转化成一个VRPTW 软时间窗问题，以实现在较低的配送成本下达到较高的配送服务水平的目标。构建的目标函数和约束条件如下：

1.7 分组和随访 根据患者术后1年内临床转归分为存活组（136例）和死亡组（56例），随访患者术后1年内生存情况，住院期间通过住院医疗记录进行随访，院外随访采用门诊或电话联系患者或其家属进行。

式（1）表示是配送总成本目标函数，当目标函数值越小，则获得越低的配送成本和配送时间，配送路线越合理；式（2）表示配送车辆的载重不得超过车辆最大装载能力；式（3）表示每个配送点由一辆车服务；式（4）表示配送车辆v 在配送点j之前只服务了配送点i；式（5）表示配送车辆v 在配送点i 之后只服务配送点j；式（6）表示配送线路的起点终点都是临时存储点；式（7）至式（9）表示决策变量约束条件。

（2）求解算法

带时间窗的车辆路径问题求解复杂，是经典的NP 难题。而基于概率的模拟退火算法以固体退火为原理，在搜索解的过程引入了随机因素，可以有效避免陷入局部极小并最终趋于全局最优。因此，本文采用模拟退火算法对VRPTW 软时间窗模型进行求解。

（3）求解步骤

步骤一：由一个产生函数从当前解产生一个位于解空间的新配送路径方案。

步骤二：计算与新配送路径方案所对应的目标函数差。

步骤三：判断新配送路径方案是否被接受。

步骤四：当新配送路径方案被确定接受时，用新方案代替当前方案。

（4）求解过程

在计算机上运行MATLAB R2016a 并编写模拟退火算法程序进行求解。输入相关的配送数据。经多次调试，将参数初始温度设置为100，冷却因子为0.99，里外层循环最大迭代次数分别为300、2 000，选择交换、逆转、插入结构的概率分别为0.2、0.5 和0.3 并进行计算。经多次迭代，在大量结果中选择最优值作为最终结果。每辆车走一条路线，临时储存点配送方案如表5所示。

一条路线安排1 辆车进行配送，因此表5 输出的8 条路线表示1 次配送需要8 辆车，将各路线的配送费用进行相加，得出每次配送费用为6 396.5 元。社康中心的配送频率为1 次/月，则月总配送费为6 396.5 元。

表5 临时储存点配送方案表

1.3.3 医院配送路径设计

（1）构建VRPTW 硬时间窗模型

疫情期间医院抗疫负担重，对检测试剂、治疗药品、疫苗等抗疫物资需求量大。若抗疫物资无法按时到达，则可能拖延救治进程，甚至付出生命的代价，需对其提供高水平的配送服务。为在满足医院抗疫物资配送高要求的同时兼顾企业运营成本，本文在设计医院配送路径时加入6 小时内必须到达的硬时间窗限制，即允许最晚到达时间LT 为6。在保证能够满足医院的高配送时效要求的前提下，构建配送成本目标函数，将其转化成一个VRPTW 硬时间窗问题，求其最优解以实现路程最短、成本最小、时效性高的目标。构建的目标函数和约束条件如下：

式（10）表示配送总成本目标函数，目标函数值越小，配送成本越低，配送路线越合理；式（11）表示配送车辆的载重不得超过车辆最大装载能力；式（12）表示每个配送点由一辆车服务；式（13）表示配送车辆v 在配送点j 之前只服务了配送点i；式（14）表示配送车辆v 在配送点i 之后只服务配送点j；式（15）表示配送线路的起点终点都是临时存储点；式（16）表示到达配送点i 的时间不晚于允许最晚到达时间；式（17）表示到达配送点j 的时间不晚于允许最晚到达时间；式（18）至式（20）表示决策变量约束条件。

（2）求解过程

在计算机上运行MATLAB R2016a 并对上述函数进行编码，利用模拟退火算法求解。输入相关配送数据。经多次迭代计算，程序输出的最优结果如表6 所示。

表6 表示一次配送需要5 辆车各走1 条路线，将各条配送路线的费用相加得出每次配送费用为4 114.7 元。由于每月对医院的配送频率为6 次，则月总配送费为24 688.2 元。

表6 临时储存点运输方案表

由于需要保护商业数据，企业无法提供原本的具体配送成本及方案。但通过在A 医药公司调研，了解到原本的配送方案存在缺货率高、配送成本费用率高的问题。而通过租赁3 个临时储存点，并按照社康中心和医院对配送时效要求不同的特点，设计最佳配送路线可有效降低缺货率及配送费用，提高A 医药公司抗疫药械配送服务水平。

2 结束语

在新冠肺炎疫情的背景下，医药流通企业在执行配送任务时，面临着平衡时效性和经济性的难题。本文以A 医药公司为例，提出设立临时储存点，针对社康中心和医院分别构建软、硬时间窗VRPTW 模型，并通过模拟退火算法求解得出配送路径，以取得时效和经济的平衡。通过研究A 医药流通企业针对珠三角的抗疫物资配送，针对性地设计抗疫物资配送方案，为医药企业基于抗疫需求的物流运作提供了有益的借鉴。