基于主题嵌入表示的商品分仓问题研究

刘 顺，黄 林，宋维林 LIU Shun, HUANG Lin, SONG Weilin

（1.华南理工大学，广东 广州 510006；2. 中国联通互联网服务运营中心，广东 广州 510006）

0 引 言

随着电子商务的发展，消费者线上消费需求已经由商品本身延伸到商品背后的服务体验。对于消费者而言，需求响应速度是影响网上购物体验的重要因素之一。不少电商企业都通过快速响应来获得客户的青睐，从而在消费市场中取得竞争优势，比如京东的“次日达”服务（消费者当天下单，次日就能送达）以更快速的响应速度为消费者提供配送服务。

分仓备货缩短了商品与消费者之间距离，从而满足消费者的快速响应需求，成为电商企业关注的焦点。分仓备货服务是指由电商商家根据各地区历史销售情况，提前通过物流公司将商品在消费者附近进行备货，提供就近发货、快速配送等服务。对于电商企业来说，分仓备货不仅缩短消费者的收货等待时间，满足消费者物流时效需求；还实现分区域就近发货、就近配送，将供应链上流动的库存尽可能按需推向靠近消费者的终端，有效降低了物流配送成本。

然而，在分仓备货的背景下，越来越多的订单被拆分配送（以下称为拆单），这给电商企业带来了新的困扰。消费者在网上下达一份订单，若订单中的商品不在一个仓库，那么该订单则会被拆分成若干个子订单，由对应的仓库完成配送。拆单不仅降低了消费者的体验，还大大增加了电商企业的配送成本。如图1 所示，拆单导致不一致的送达时间，需要消费者多次取货。另一方面，拆单也导致电商企业多次重复处理同一份订单，产生了额外的运输和运营成本。

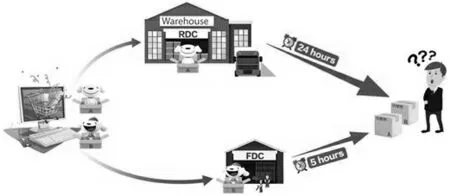
图1 顾客在网上下达一份订单，由不同仓库送出导致不一致的送达时间

为了降低甚至减少拆单量，一个很自然的想法就是将同一个订单下的商品放进同一个仓库。基于此，近年来已有部分工作被投入到该问题的研究。Catala以最小化拆单量为目标，将拆单问题归结为一个混合整数规划模型。文中指出该问题属于NPHard 难题，并基于贪心思想设计出热销品算法求解模型。不同学者从不同角度对该算法进行改进，李建彬等人在热销品算法的基础上提出了环形优化算法（Loop）。环形优化算法将商品按销量排序，并构成一个环形，进而通过贪心思想获得分仓结果。钟丽文等结合关联规则算法，寻求订单中具有强关联关系的单品，提出贪婪关联算法。

上述算法设计的基本思路都源于贪心算法，即优先考虑包含高频商品的订单拆单问题。热销品算法将热销品分配给每一个仓库，环形优化算法在商品构成的环形中，优先将销量最高的头部商品分配给每个仓库。贪婪关联算法通过关联规则来筛选高频率的商品组合，然后分配给每个仓库。以上研究能解决包含高频商品的拆单问题，然而，在实际的物流生活中，一方面，商品品类规模空前庞大，另一方面，随着品类的扩大，顾客的购买行为也呈现个性化的趋势。因此，商品的长尾效应愈发凸显，把算法设计的重点放在头部商品上，已不是一个合适的选择。

本文在原有研究的基础上，提出了主题嵌入聚类算法来将商品合理的分配给多个仓库，使同一个订单下的商品尽可能在同一个仓库，从而降低订单的拆分配送量。算法首先通过主题嵌入表示（Embedding with Topic Model, ETM） 获得蕴含商品关联信息的嵌入表示，再通过聚类算法获得分仓结果。实验的评测结果体现了所提出算法的优越性。

1 商品分仓模型以及求解算法

本节首先以最小化拆单量为目标，建立拆单模型，然后提出主题嵌入聚类算法来求解模型。

1.1 商品分仓模型

本小节从商品分仓的角度来考虑拆单问题，如前言所述，本文考虑的问题可描述为如何将品类繁多的商品合理地分配给若干个仓库，使得订单的拆分配送量最小化。

约定如下符号：

V= {v,v,…,v}：待分仓商品集合；

S= {s, s,…,s}：仓库集合；

O= {o,o,…,o}：订单集合；

X：订单指派矩阵，如果商品v在仓库s中，x=1，否则x=0；

Y：订单拆分向量，其中每个元素y表示对应订单o被拆分的数量。对于包含若干个商品的订单o，根据决策变量得到商品分仓结果之后，若订单中的商品分仓存储，该订单就会根据分仓结果被拆分成若干个子订单：

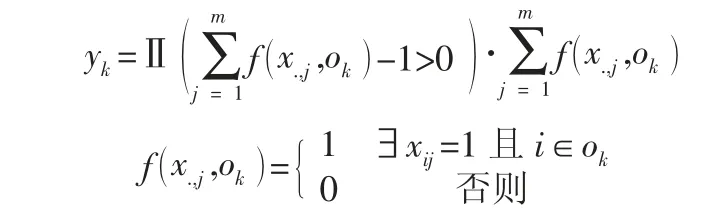
根据以上的符号，上述问题可归结为一个组合优化模型，如下所示：

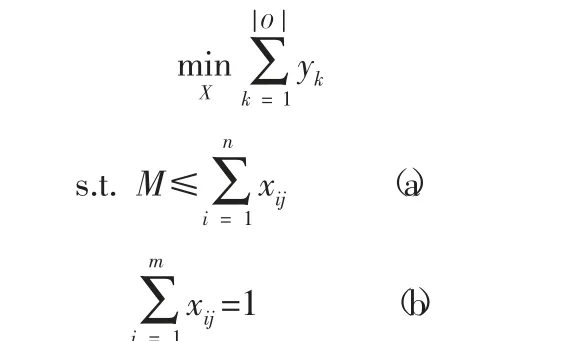
优化目标函数表示找到一个合理的商品分仓决策，使得拆分配送的总订单量最小。约束（a） 表示每个仓库至少需要存储M 个商品。约束（b） 限定了每个商品被一个仓库储存，仓库之间储存的商品并不重合。

1.2 求解算法

本小节提出嵌入聚类算法来求解模型。算法分为嵌入表示和聚类两部分。

嵌入表示：

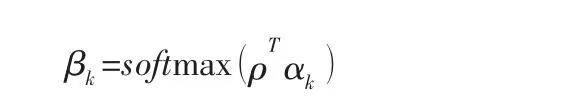
基于以上表示，第d 份订单的生成过程可以描述为：

（1） 生成订单—主题分布θ～LN (u,∑ )。

（2） 对于订单中的第n 个商品：

①从主题分布θ中采样得到一个购物主题编号z；

②从该主题的词汇分布β采样商品w。

其概率图模型如图2 所示。

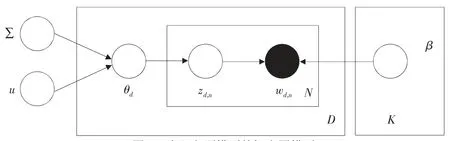
图2 嵌入主题模型的概率图模型

其中，LN (u,∑ )表示逻辑斯蒂正态分布，u,∑表示控制分布的均值向量和协方差矩阵，上述过程描述了在指定参数设置的条件下“正向”的订单生成过程。然而商品的嵌入表示作为嵌入主题模型中的隐层参数，在现实的生活场景中是不可见甚至不存在的，需要“逆向”的根据商品销售数据，获得各个商品的嵌入表示。B. Dieng 等人提出了一种变分推断模型用于主题嵌入模型（ETM）的求解，由于本文的数据产生模型与文献[10]中生成模型完全一致，所以可以把文献[10]中的求解模型应用于本文。

聚类：

注意到嵌入表示ρ 包含了商品之间的关联信息，可以通过嵌入表示向量之间的欧式距离来量化节点之间的关联性。因此本文将原问题转化为一个约束聚类问题，具体如下所示：

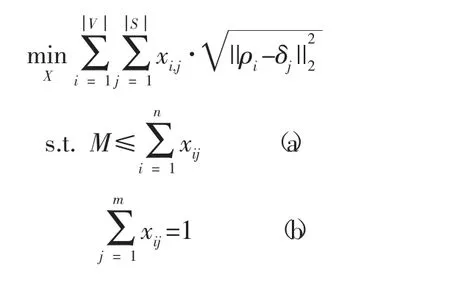
δ表达为：

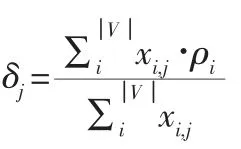
ρ表示矩阵ρ 的第i 行，作为第i 个商品的嵌入表示向量，δ代表第j 个聚类簇的聚类中心。Bradley 等提出一种基于最小费用流的约束聚类的求解算法。由于上述的聚类模型和文献[12]中的问题完全一致，因此直接将文献[12]中的约束聚类算法应用于本文来获得商品分仓的结果。

综上所述，算法首先通过文献[10]主题嵌入模型（ETM） 获得蕴含商品关联信息的嵌入表示，然后利用嵌入表示通过文献[12]约束聚类算法得到商品分仓的结果，由于算法由主题嵌入表示和聚类算法构成，因而本文称之为主题嵌入聚类算法。

2 算例分析

2.1 实验设置

数据描述：Ecommerce 数据集包含了一家英国的在线零售店从2010 年至2011 年期间发生的所有交易，共包含2 万份订单和4 千多个不同种类的商品。数据集中有超过90%的销售订单包含了2 个以及2 个以上的商品。

测试协议：根据本文的研究问题，计算订单的拆分配送率来评估所选择商品组合的好坏。对于订单集中的每一份订单O，如果订单中的商品都在同一个仓库，那么无需拆分配送，记y=1，否则，y=0。则订单拆分配送率定义如下：

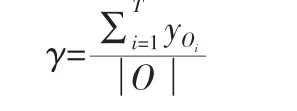
对比算法：本文采用文献[4]中的环形优化算法作为对比算法。此外，为了探究商品关联信息是否对商品分仓的结果起到正向的提升作用，设计一种随机选品算法作为对比算法，算法将待分仓商品集中的每一件商品随机指派给任意一个仓库。在这个算法中，商品的分配是随机的，未考虑任何的商品之间的关联信息。

2.2 实验结果

本小节首先利用t-SNE技术，对嵌入表示可视化展示，接着上述的实验设置下，对比分析不同算法得到的结果。

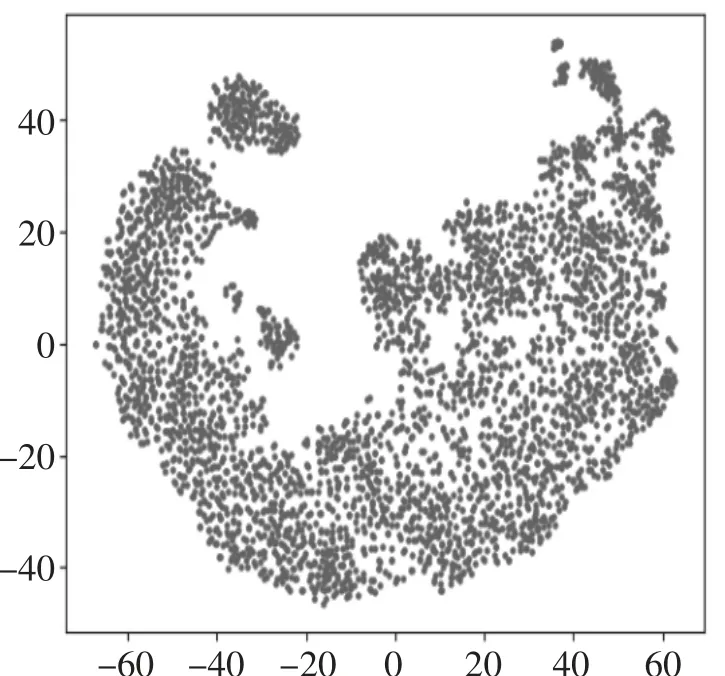
图3 利用t-SNE 技术可视化商品的嵌入表示

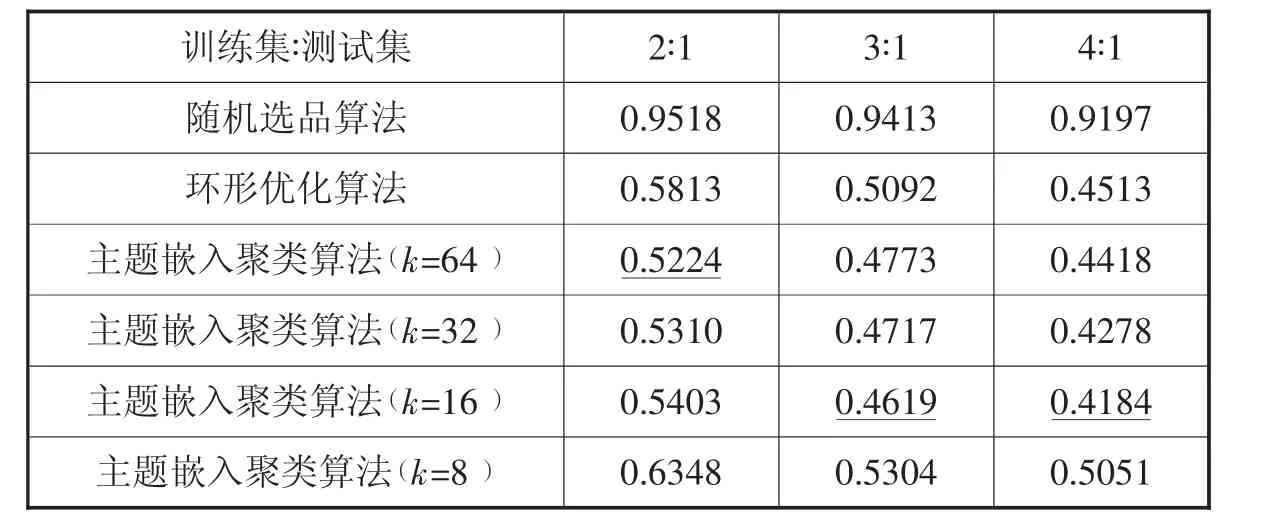
表1 不同算法得到的拆单率的大小（拆单率越小越好）

通过观察算法在不同比例数据集上的表现，得出一个主要结论：主题嵌入聚类算法能有效利用商品的关联信息生成更好的商品分仓结果。在不同的训练集比例下，相较于随机选品算法，主题嵌入聚类算法有显著的优势。在大部分参数设置下，主题嵌入聚类算法能比环形优化算法取得更好的效果。实验结果表明通过主题嵌入表示能提取出订单数据中蕴含的商品关联信息，利用该嵌入表示，能获得更好地分仓结果，从而降低拆单率。

3 结 论

商品的销售记录作为反映消费者需求和企业运营状况的关键数据，在实业界和学术界中都是研究者进行研究和分析工作的基础。在本文的研究中，提出了主题嵌入聚类算法来获得商品分仓结果。算法从商品的销售记录着手，利用嵌入主题模型得到商品的嵌入表示，在嵌入表示的基础上进一步通过聚类算法获得商品分仓的结果。实验表明，本文所提出的算法具有显著的优越性。

本文所提出的主题嵌入聚类算法在其他领域也有应用，如在智能客服领域中，一个重要的问题是如何将客户反馈的文本信息迅速的总结归类，利用本文提出的嵌入聚类算法可以将相似的词语划为一类，进而快速总结反馈信息，为业务提供支撑。