《配送中心作业管理》课程教学改革探讨——基于节约里程法的安庆市食品业配送路径优化设计

何丽萍，王 瑛，段春晖，李玉洪 HE Liping, WANG Ying, DUAN Chunhui, LI Yuhong

（安庆职业技术学院 现代商务学院，安徽 安庆 246000）

1 节约里程法的主要原理及基本思想

节约里程法是一种有名的启发式算法，可以用来解决运输车辆数目不确定的问题。它是指多个客户的配送由一个集中供应配送点完成。使用这种方法，具有三个前提条件，即：有且只有一辆配送车辆满足该条线路上任意客户的需求，提供送货服务；配送车辆的额定配载量大于等于任一路线上客户的需求量总数；任意一条配送路线的巡回里程不超过配送车辆一次配送的最大行使里程。

1.1 节约里程法的主要原理。配送车辆选择一个送货目的地，从配送中心（集中供应配送点） 出发，送达货物后原路返回至起始地，利用以此种方式，把所有客户的货物依次送达完，从而形成原始的配送路线方案。根据三角形定理，第三边小于两边之和，合并送货的过程中的往返回路，在满足车辆里程和额定配载量的限制前提下，当节约的总里程经过合并后达到最大值时，则对下一辆的配送路线进行优化，直到总的配送里程达到最优，形成最佳的配送线路方案。1.2 节约里程法的基本思想。在满足上述三个前提条件的情况下，根据配送中心到各个客户之间的里程和各个客户之间的相对里程以及自身的运输能力，制定出使总的配送车辆吨公里数最优的配送方案，配送车辆根据此方案，按照顺时针或者逆时针的方向依次为目标客户送货。节约里程法的基本思想如图1 所示，P 为配送中心，客户收货点分别为X 和Y，各点之间的距离分别用x,y,w 表示。原始的配送路线方案为：客户X、Y 分别有一辆车为其配送，两辆车产生的里程和为2 x+( )y 。但如果改用另外一种配送路线方案，即用一辆车采用环形“闭合回路”配送方式，配送里程和则为x+y+w。在不考虑特殊情况，如道路因素的影响，对比第一种及第二种方式，可以看出，后者比前者的里程数节约了x+y-w，这个数值即为“节约里程”。

图1 节约里程法的基本思想示意图

2 目前安庆市食品业配送存在的问题

配送作为现代物流中的重要环节，直接影响着企业的利润，然而，就我国配送现状而言，其水平还有待提高。对于安庆市食品业来说，同样存在着相关的配送问题。主要表现在以下几个方面：第一，配送信息化程度低。对于食品业来说，其服务的客户遍布在各个角落，客户的订单多样，很难建立一个有效的信息系统处理相关订单，并按照订单客户合理的优化配送路线，这就导致了信息沟通不畅，信息流通效率低。第二，高素质的物流人才缺乏。该食品业配送中心的大多数员工要么只具有实践技能，要么空有理论基础，对于既有厚实的理论基础，又具有丰富的实践经验的员工少之又少。第三，运力安排不当。目前该食品业配送车辆共有6 辆，其中载重量4 吨和2 吨的车辆分别为2 辆、4 辆。当有订单需求时，该食品业往往根据经验，经常性的使用2 吨的车辆进行配送，这就造成了2 吨车辆极高的使用率。同时，当客户需求较多时，还会出现2 吨车辆供不应求的现象。而4 吨的车辆却长期闲置，很少被使用，导致运力安排不合理。第四，配送线路安排不合理。由于客户需求不一样，订货时间不固定，以及信息化水平的低下，当出现客户订单时，配送的具体线路以及配送的先后顺序大多按照司机的个人经验，这就会造成配送路线安排的不得当。

对于该食品业出现的上述配送问题，短期内不能一一得以解决，因此本文结合《配送中心作业管理》课程内容中的“节约里程法”的知识点，针对上述第三点以及第四点存在的问题进行优化。

3 节约里程法的模型构建

3.1 模型描述。当有多个客户订单生成时，配送中心就要向多个客户配送货物，此时就需构建基于节约里程的路线优化模型。本文以安庆市食品业配送中心为例，以其客户配送为背景建立相应的模型。

3.3 模型构建。构建以Z 最小时的目标函数，Z 代表食品业配送中心向所有客户配送的里程总量，按照上面相关变量，建立如下配送路线优化模型：

在上述配送路线优化的模型中，式（1） 所代表的意思为：一个客户的货物只能由Q 辆车中的其中一辆来完成配送，配送车辆总数Q 用来完成所有客户的配送任务；式（2） 所代表的意思为：所有的配送路线中不管是哪一条，配送车辆的额定配载量都是大于等于此条路线上客户的需求量总数；式（3） 所代表的意思为：无论是哪一条配送路线上的里程总数都小于等于此路线上车辆的单次行使里程最大值；式（4） 所代表的意思为：在一次配送安排中，所有的客户唯有一辆配送车辆到达装载地；式（5） 所代表的意思为：在一次配送安排中，所有的客户唯有一辆配送车辆离开装载地。

4 食品业配送路线优化设计

本文以安庆市食品业配送中心及与10 家客户之间构成的相关数据资料为基础，以此验证该模型的有效性。食品业配送中心及10 家客户之间构成的配送网络图如图2 所示，图2 中连线上的数字表示公路里程，单位为km，每个客户对货物的需求量，用临近客户括号中的数值表示，单位为t。该食品业配送中心可供使用的汽车的载重量分别为2t 和4t，且配送车辆一次循环里程在45km 范围内。

图2 食品业配送中心与10 家客户之间的配送网络图

4.1 优化前的配送方案。该食品业配送中心P 在配送路线优化之前采取的是一对一往返的配送方式。即配送中心根据客户的订单，分别向10 家客户依次送货。优化前的配送方案下的配送网络图如图3 所示。

根据图3 可知，配送中心要完成10 家客户的配送任务，需来回往返10 条线路，分别为：PA、PB、PC、PD、PE、PF、PG、PH、P-H-I、PJ。此时需要10 辆2t 的配送车辆。按照原始的方案，完成10 家客户的配送任务所行使的配送里程为：4.2 优化后的配送方案。运用配送路线优化模型（节约里程法模型），优化设计出10 家客户新的配送路线。

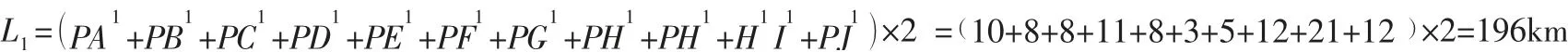
图3 优化前的方案配送网络图

第一步：计算最短距离（食品业配送中心及各客户之间）。计算结果如表1 所示：

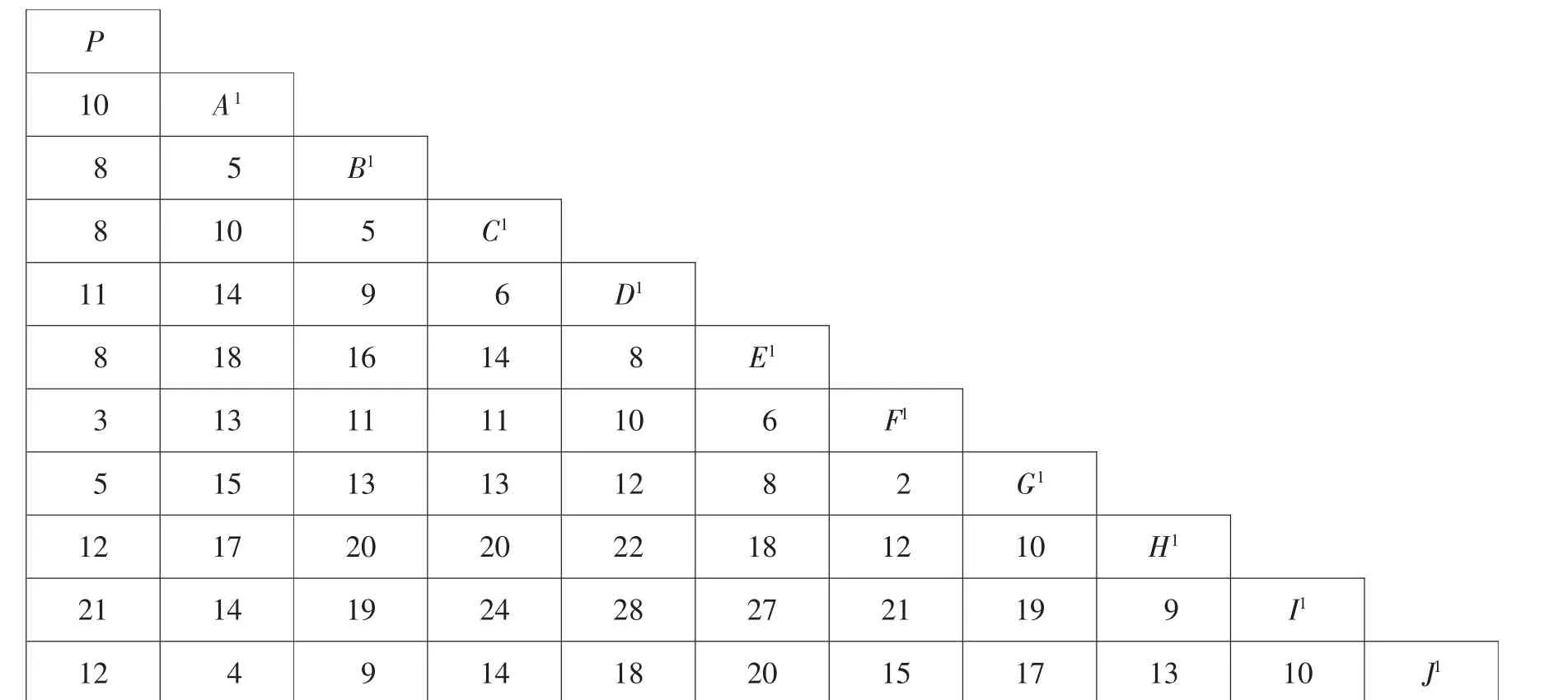
表1 最短距离表

第二步：计算节约里程。根据节约里程法的基本原理，A到J客户中的任意两个客户由食品业配送中心进行配送，计算节约的里程。例如，向A、B两家客户配送，可以节约的里程为：

按照上述原理，依次计算出食品业配送中心与10 家客户中任意两家组合可以节约的里程，如表2 所示。

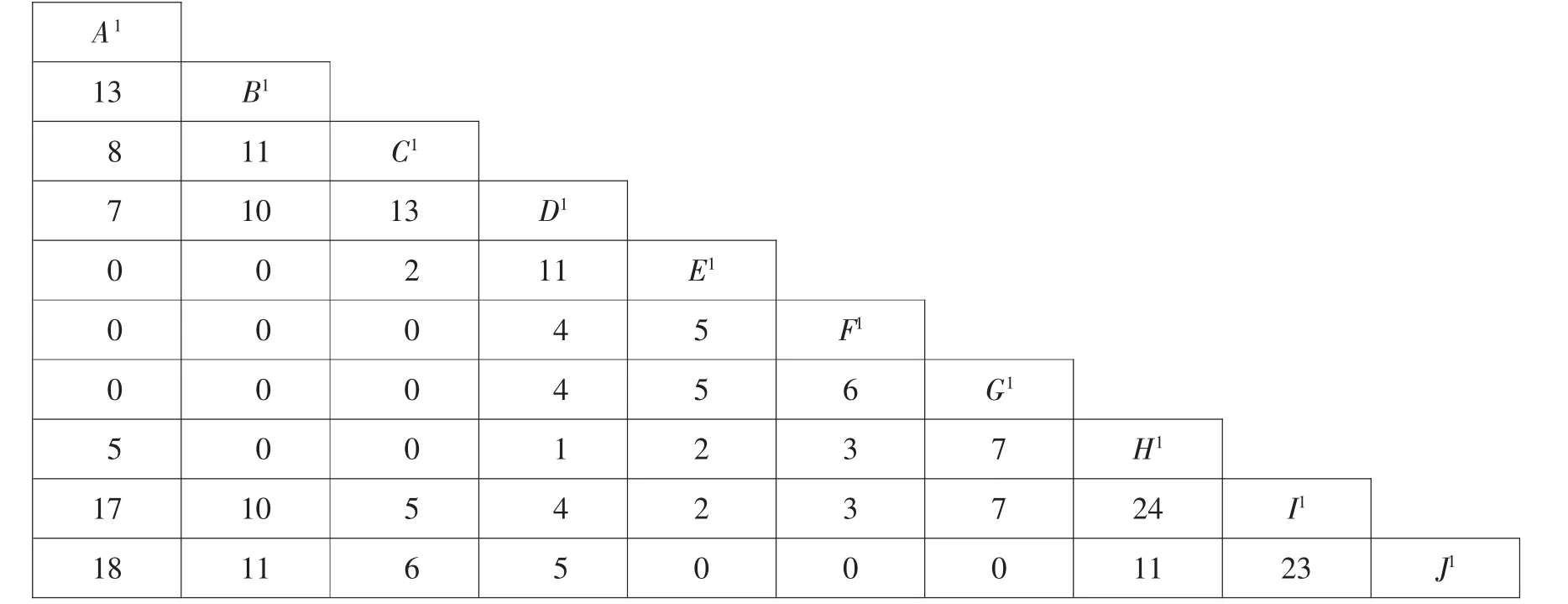
表2 节约里程表

第三步：将节约的里程进行排序。按照从大到小的顺序对节约的里程排序，得到结果如表3 所示。

表3 节约里程排序表

第四步：确定配送路线。根据约束条件，按照节约里程由大到小的顺序，连接HI、IJ、AJ，形成第一条巡回线路P-H-I-J-A-P，行使里程为45km，载重量为3.9t，需要载重量为4t 的车辆1 辆；连接BC、CD、DE，形成第二条巡回线路P-B-C-D-E-P，行使里程为35km，载重量为3.9t，需要载重量为4t 的车辆1 辆；连接F、G，形成第三条巡回线路P-F-G-P，行使里程为10km，载重量为1.7t，需要载重量为2t 的车辆1 辆。由此得出最终的配送路线方案，如图4 所示。

根据图4 可知，配送中心要完成10 家客户的配送任务，需要2 辆4t、1 辆2t 的配送车辆。按照优化后的方案，完成10 家客户的配送任务所行使的里程为：L=45+35+10=90km。

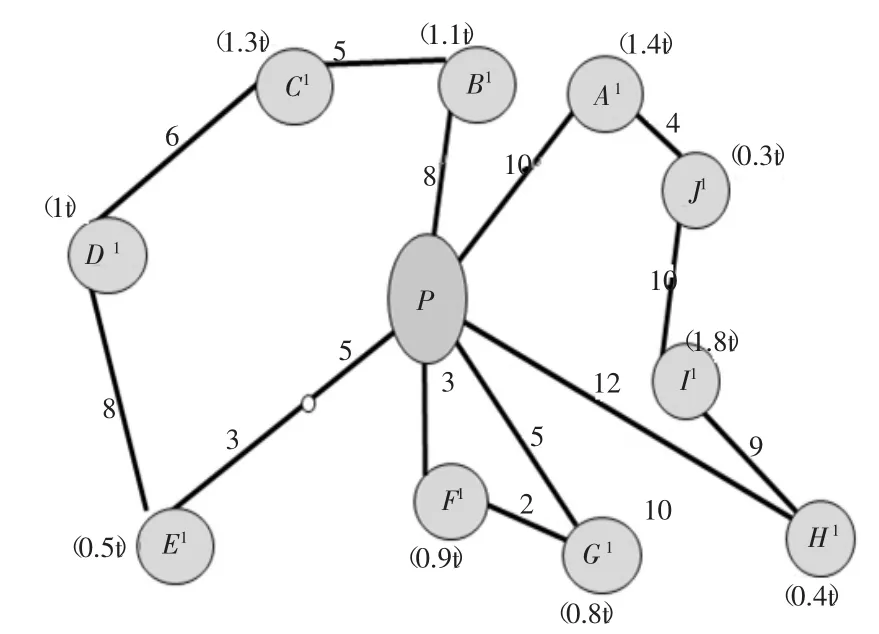
图4 优化后的方案配送网络图

4.3 优化前后的配送方案对比。配送方案优化前后不管是行使里程、使用车辆还是配送路线数量得到了优化，具体见表4 配送方案优化前后对比表。

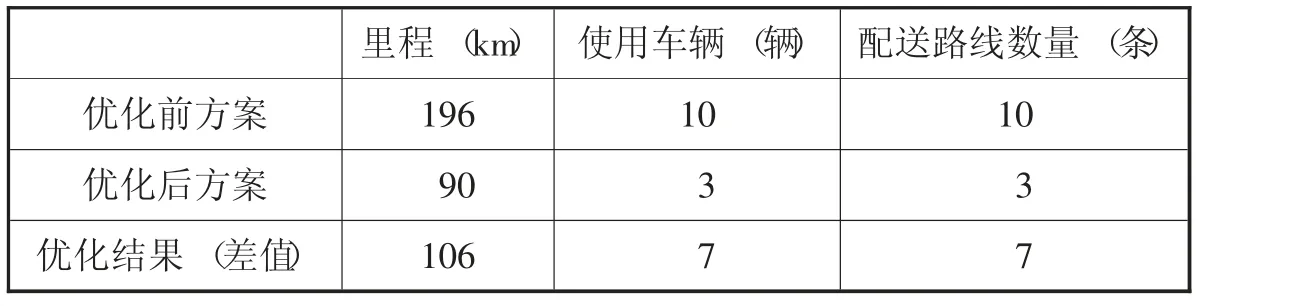
表4 配送方案优化前后对比表

5 结束语

配送在物流活动中地位不可替代，本文通过《配送中心作业管理》课程教学改革，结合分析安庆市食品业配送中心存在的配送信息化程度低、高素质的物流人才缺乏、运力安排不当、配送线路安排不合理问题，利用节约里程法的主要原理、基本思路及模型的构建，优化设计出新的配送路线，并形成了最终的配送路径方案。对提高企业的配送效率、节约企业的物流成本都具有重要的意义，同时也让学生们提高了解决配送中的路径优化实际问题的能力。