银行业信用风险的多维多重传染效应及其因素研究

王周伟，苏荣培

（上海师范大学 商学院，上海 200234）

一、引言

风险传染是指一个或几个系统重要性金融机构经营失败，通过关联网络发生风险传递，导致关联金融机构陆续陷入困境。其核心特征在于金融机构信用质量恶化风险的传染。因此银行的风险水平及其传染的测度就是要测度其实质性表现的严重程度。目前主流测度指标有：（1）条件风险价值（CoVaR）与增量条件风险价值；（2）条件预期亏空（CoES）和增量条件预期亏空；（3）系统性风险指数（SRISK）与成分系统性风险指数；（4）成分系统违约距离或系统违约率。四类指标各有优劣。前三类指标的优势在于合理测度了风险的绝对损失及绝对传染损失，但没有考虑银行业风险承担能力和风险缓释能力，没有合理测度剩余信用风险损失；第四类指标把金融业看作一个整体，考虑了宏观经济冲击下金融体系的内生风险，却没有考虑金融体系内的风险关联传染和协整联动。利用已有指标估算整体风险传染，会产生重大模型设定偏误，而银行业是金融中枢，银行风险传染水平的合理测度尤为关键。因此，针对系统性风险实质性表现——信用风险传染，本文创新性地利用KMV模型测度银行信用风险，通过Copula函数构建联合分布函数，估算期间联合违约率均值，以测度信用风险传染，并在风险传染网络框架中验证信用风险传染的影响因素。

二、文献综述

（一）单个银行信用风险测度

对于单个银行的信用风险的测度，主要的做法有三种。第一种是直接使用银行事后的银行风险监管指标作为银行信用风险的度量指标，相关文献使用不良贷款率作为银行信用风险的代理指标，如陈昆等（2019）、王晓等（2019）和朱明秀等（2013）。除了使用不良贷款率作为代理指标外，有些文献还使用拨备覆盖率作为稳健性检验时的代理变量，如王晓等（2019）。第二种是使用银行财务报表中的数据构造出银行信用风险评价指标，如杨天宇等（2013）和李硕等（2020）使用资产收益率以及银行资本和资产的比率来计算Z值，刘志洋（2016）使用不良贷款余额与上一期贷款减值准备的比值作为银行信用风险指标。第三种是使用KMV模型来计算单个银行的违约距离以及对应的违约概率，如万言等（2012）；或采用KMV模型的扩展形式CCA模型来计算违约距离，如王培辉等（2017）；还有研究将资产价格存在跳跃的情况纳入到违约距离的计算中，如Merton（1976）考虑存在对称的跳跃过程，Kou（2002）则考虑存在着非对称的跳跃。

（二）银行业信用风险测度

金融机构之间的信用风险关系可以大致区分为两类，一类是信用风险的传染，另一类是机构间的信用风险的关联。前者主要集中于用复杂网络的方法来验证机构之间的信用风险传染问题，并通过仿真模拟的方式分析影响信用风险传染的因素；后者则只使用CDS、CCA或者KMV的方法计算单个机构的信用风险水平，之后通过Copula的方法计算信用风险的关联程度或者联合违约概率（JPoD）。对于第一类风险，关于银行信用风险复杂网络的构建，大多数文献采用银行间的借贷关系、双边同业资产负债关联和CDS等来衡量银行之间信用方面的关联。信用风险传染网络主要是由各银行之间的债务相互关联、资产互相持有引起的，因此信用风险复杂网络的构建首先就是利用这种资产和债务的关联关系。对于第二类风险，机构间信用风险，主要使用违约距离或者违约概率来测度风险之间的同步关联关系，而连接的方法主要是Copula函数。违约距离用来计算信用风险相依关系，主要是使用Copula方法来计算违约距离序列之间的相依系数，如周利国等（2019）使用Joe-Clayton Copula方法、申敏（2016）使用一系列Copula方法分别计算出企业之间、银行之间的相依系数；联合违约概率主要使用CIMDO方法和传统Copula方法计算，但主要被用于资产组合的配置中，较少用于衡量银行业整体的信用风险水平。

（三）银行风险传染的影响因素

银行风险传染的影响因素大致分为银行信用质量因素、风险传染网络因素和国内外宏观经济因素三个方面。

银行信用质量因素方面，多数研究是以不良贷款率（NPL）、资本充足率（CAR）、存贷比和净资产收益率等银行个体特征变量作为信用风险传染的微观因素。如丁德臣（2016）选用资本充足率、不良贷款率、应收账款周转率等银行微观层面指标衡量非经常性的风险传染；叶永刚等（2018）选用权益占比、不良贷款率占比等指标，构造银行行业预警指标体系。

风险传染具有网络属性，有研究引入风险溢出网络的结构特征指标验证其对风险传染的影响，如胡利琴等（2018）将加权平均连接度和特征向量中心度纳入到风险传染模型中；宫晓莉等（2020）将网络结构的特征向量中心性纳入到风险预警的机器学习因素中。

在宏观经济因素方面，多数研究用GDP增速、CPI和M2增长率等经济指标来衡量宏观经济冲击，如叶永刚等（2018）利用GDP增速、政府债务占GDP比率、M2与GDP的比值等指标，构造外部宏观环境预警指标体系；郭卫东（2013）用MES方法测度风险传染贡献，认为银行自身的不良贷款率、杠杆率和总资产收益率是决定其对整个金融系统风险边际贡献度的重要因素；还有研究将国际金融因素加入国内金融风险传染的预警中，如李雪松等（2019）认为金融周期和美联储加息会显著增加金融危机发生概率。

三、银行信用风险传染效应的测度方法设计

（一）信用风险传染的核心与测度思路

通常意义上风险传染的核心源头是系统重要性机构的违约破产，这样风险传染测度的重点与传染的风险最终都是银行信用风险。而目前测度风险传染的主流指标有：（1）增量条件风险价值（ΔCoVaR）；（2）增量条件预期亏空（ΔCoES）；（3）成分系统性风险指数（CSRISK）；（4）成分违约距离或成分联合违约率。前三类指标主要测度的是给定置信水平下的风险绝对损失，难以测度剩余信用风险发生的可能性。而第四类指标，即或有权益分析法（CCA）及其违约距离类指标，如简单平均违约距离（ADD）、资产加权违约距离（WDD）和组合违约距离（PDD）等，是银行业信用风险传染测度的主要方法。该方法反映了金融机构的信用风险传染，但是把金融机构行业作为一个整体测度违约风险，忽略了金融机构之间的传染风险与联合违约问题，而信用风险传染是风险传染的最终体现，正是风险传染机制使系统重要性机构的单一风险放大演化为整个金融系统的风险。

因此，在CCA方法基础上，依据信用风险关联传染的含义，可以利用KMV模型估算单个银行的预期信用风险，通过Copula函数拟合任意两家银行的信用风险关联，构建二维联合分布函数，估算任意两个银行的联合违约概率（JPoD），分析期内任意两个银行的联合违约概率序列的平均值，即期间联合违约概率代表其关联违约，可以构建银行信用风险关联传染矩阵。进而，利用某银行与其他所有银行的期间联合违约率均值，可稳健测度银行业信用风险传染。

（二）利用KMV模型评估单个银行的预期违约率

目前主流的商业银行信用风险测度模型是KMV模型、Credit Metrics模型、Credit Risk+模型和Credit Portfolio View模型等。其中，KMV模型的建模理论体系完整，综合利用资本市场和财务信息，能前瞻性地有效预测未来信用风险。本文选用KMV模型测度单一银行的信用风险，模型设定参考蒋彧等（2015）的做法。

KMV模型认为，公司资不抵债时会发生违约，一个上市公司的股权价值就是以公司的总资产为标的资产，公司债务价值为执行价格的欧式看涨期权价值。利用Black-Scholes欧式看涨期权定价公式与违约定义，可以推导出预期违约概率（EDF）估算公式：

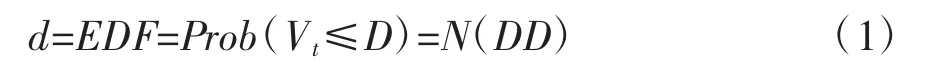
其中，V为t时刻（t=1，2，…，T）的公司资产价值；D为公司负债，等于短期负债加上长期负债的一半；DD为违约距离，违约距离越大，预期违约概率越小。其计算公式为：

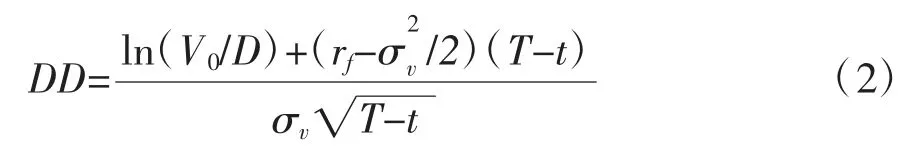
其中，r为无风险利率；σ为公司资产价值的波动率；T为负债的到期时间。

公司资产价值及其波动率由Black-Scholes欧式期权的定价公式及其delta敏感性分析公式联立求解得到。Black-Scholes欧式期权的定价公式为：

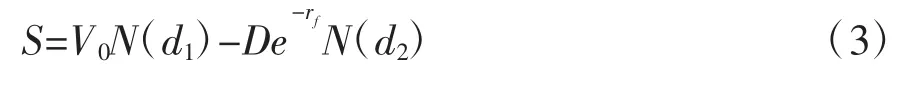
其中，d和d分别为：

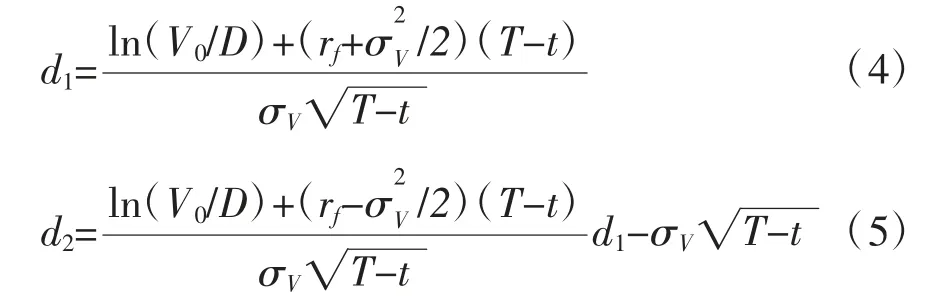
其中，S为公司的股权市场价值；V为期初公司的资产价值；N（·）为标准正态分布的累积概率分布函数。

设σ为股票收益率的波动率，则有期权delta敏感性分析公式：

（三）利用Copula函数构建预期违约概率的联合分布函数

关联传染分析方法有：Copula函数拟合相关结构法、相关系数构建相关矩阵法、DCC-GARCH模型、多元多分位数条件自回归风险价值模型、向量自相关（VAR）模型、VECM模型及其脉冲响应和广义方差分解法构建响应矩阵法、格兰杰检验构建关联矩阵法、网络模拟仿真分析法与网络拓扑分析法、空间计量分析法、资产负债业务关联矩阵法、信息熵法等。

风险关联相关传染具有不对称性、非线性特征。除了Copula函数之外，其他方法主要是刻画了金融机构风险之间的全局静态线性相关关系，但难以测度非线性、上下尾部非对称的关联相依结构特征。本文选用Copula函数来构建风险传染相关的预期违约率联合分布函数。

单个公司一段时间内的违约概率并不服从正态分布，不适合采用正态Copula函数作为连接函数。银行信用风险较高时银行风险传染关系更为强烈，而Gumbel-Copula密度函数具有上尾高下尾低的非对称性，能够较为敏感地描述上尾部强相关特性。本文采用Gumbel-Copula函数作为连接函数，构建二元联合概率分布函数，这样，利用单个公司的违约概率及其边缘分布和Gumbel-Copula函数可以计算出两两公司之间的联合违约概率序列。

Gumbel-Copula函数的表达式为：

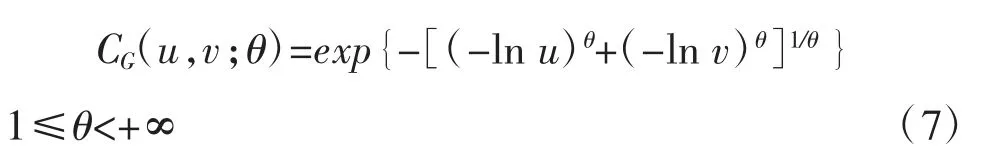
其中，u和v为任意两家银行预期违约概率的边缘分布函数；θ为要估计的Gumbel-Copula函数的参数。

（四）计算平均联合违约概率均值测度系统性信用风险传染

利用MATLAB的平滑核密度（ksdensity）函数，拟合出样本银行的联合违约概率序列的边缘概率分布函数F（d），代入到Gumbel-Copula函数（7）式中，可估计出联合概率分布函数。再依次代入任意两家银行的边缘预期违约概率值，就可以得到这两家银行联合违约概率的序列。即

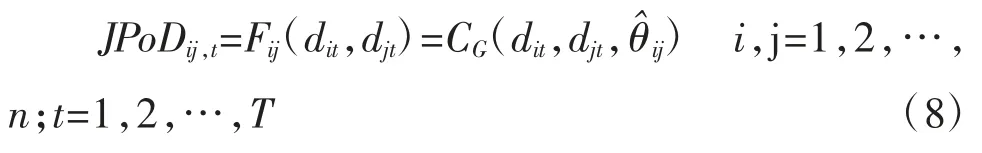
任意两个银行之间t时刻的联合违约概率一般在分析期间变化较大。为反映其集中趋势，本文计算任意两个银行给定时间段内任意时刻联合违约率的平均值，定义为期间联合违约率，反映其在分析期间同时违约的联合违约率水平，即银行i违约时银行j违约的条件违约率。其计算方式为：

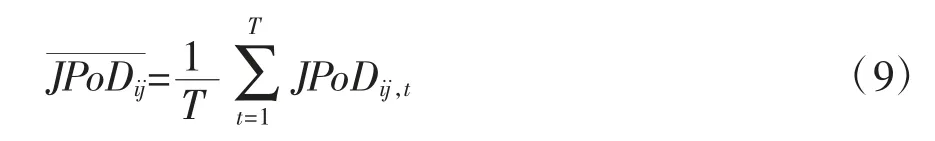
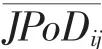
银行i的期间联合违约概率反映了银行i对任意一家其他银行的违约风险传染。在同业拆借业务关联、股市信息关联传染和持有共同资产等关联作用和宏观行业共同因素冲击共振作用下，银行i对所有其他银行都有信用风险溢出传染效应，这些信用风险溢出传染效应都可以用银行对任意一家其他银行的期间联合违约率测度。这样，银行i的总信用风险溢出传染效应就可以用其所有与其他银行的期间联合违约概率的平均值测度。所以本文对期间联合违约率矩阵的各行求均值，可以计算出银行i的期间联合违约概率的平均水平，定义为期间联合违约率均值，测度银行i对所有其他银行的违约风险溢出传染效应的总体大小，作为衡量该银行的总信用风险外溢传染效应的指标。其计算公式为：

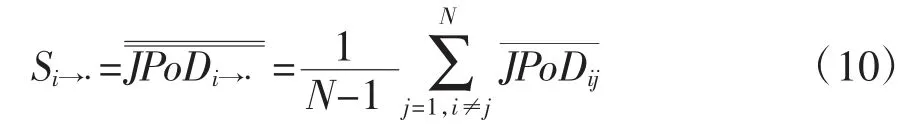
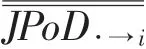
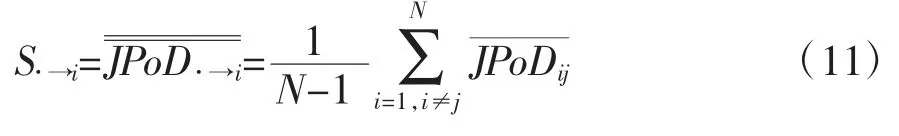
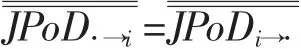
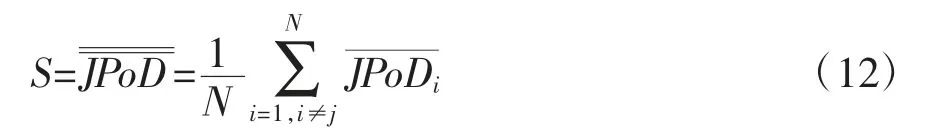
利用（10）式和（11）式的计算逻辑，构建期间联合违约概率矩阵。其与该系统性风险溢出传染指数的具体计算逻辑如表1所示。

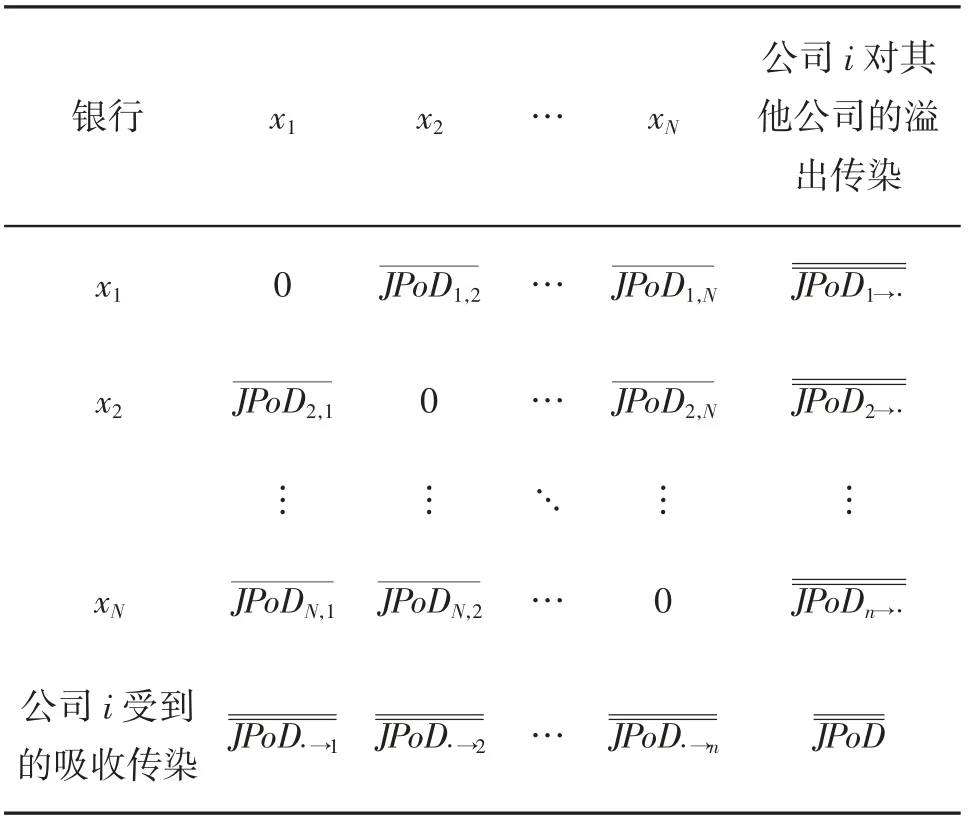
表1 期间联合违约概率矩阵与系统性风险溢出传染指数

四、银行系统性信用风险的传染效应估算结果与分析

（一）样本与数据

银行业自2007年1月1日实施新的企业会计准则，本文选取2008年之前上市的所有商业银行，共14家，其中包括4家国有商业银行、7家股份制银行和3家城市商业银行。数据选取2007年9月25日到2020年9月30日的日度市场数据和季度财务数据。

选取的银行代码和分组如表2所示。

表2 银行分组和代码

银行的股票市场价值以总市值为代表，根据每日股价可计算出日变动的股价市值。股价收益波动率以20个交易日为窗口长度，用滑动窗口的方式计算出20个交易日对数收益率的标准差，作为股价收益日波动率，之后再转换成年化股价收益波动率。公司的负债以负债总额为代表，无风险利率用一年期存款基准利率衡量，数据来源为中国人民银行公布的数据。

（二）全样本的银行系统性信用风险传染效应静态分析

把相关数据代入由（3）式至（6）式组成的联立方程组，计算出银行的资产价值和资产收益波动率，再把结果与相关参数值代入（2）式和（1）式计算出违约距离和预期违约概率。KMV模型计算结果的描述统计如表3所示。

由表3可知，预期违约概率最大值为0.8785，已达到很有可能违约的程度，由于在危机时期部分银行负债水平过高，超出估计的资产价值，KMV模型定义资不抵债即违约，从KMV模型评估看该银行大概率已经违约；预期违约概率的最小值为0，这是无金融危机时期银行的资产价值水平远高于总负债导致；预期违约概率的平均值为0.034，与银行的不良贷款率水平比较接近。

表3 KMV计算结果的描述性统计

用Gumbel-Copula函数可以得到联合违约概率的估计函数，直接利用Kendall相关系数估计全样本的Gumbel-Copula的参数θ值，结果如表4所示。

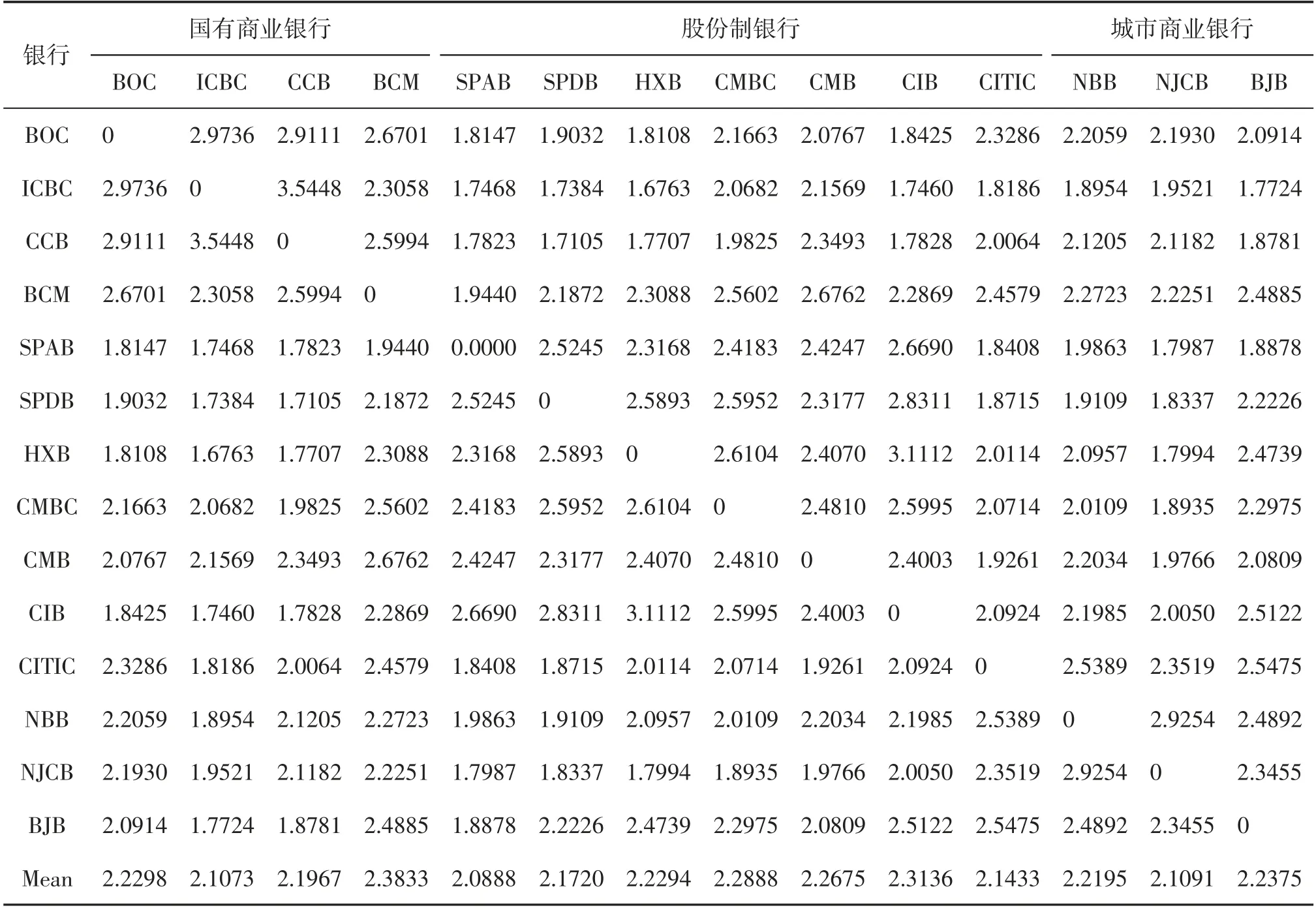
表4 全样本的Gumbel-Copula参数θ估计结果

由表4可知，所有银行的Gumebl-Copula函数的估计参数值在1.8～2.5，银行的Kendall相关系数在0.4117～0.6667，这与其余银行预期违约率之间的上尾部相关性较高，信用风险关联传染特征非常相似。

常用的Copula函数拟合检验方法有K-S检验、Q-Q图检验和卡方拟合优度检验。本文使用均匀分布的Q-Q图检验法检验Gumebl-Copula函数对任意两家银行预期违约率的相关性的拟合有效性。结果显示，Gumebl-Copula函数可以有效拟合任意两家银行预期违约率之间的不对称相关性，预期违约率相关性具有“J”形分布，上尾部相关性高，而下尾部相关性低。

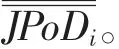
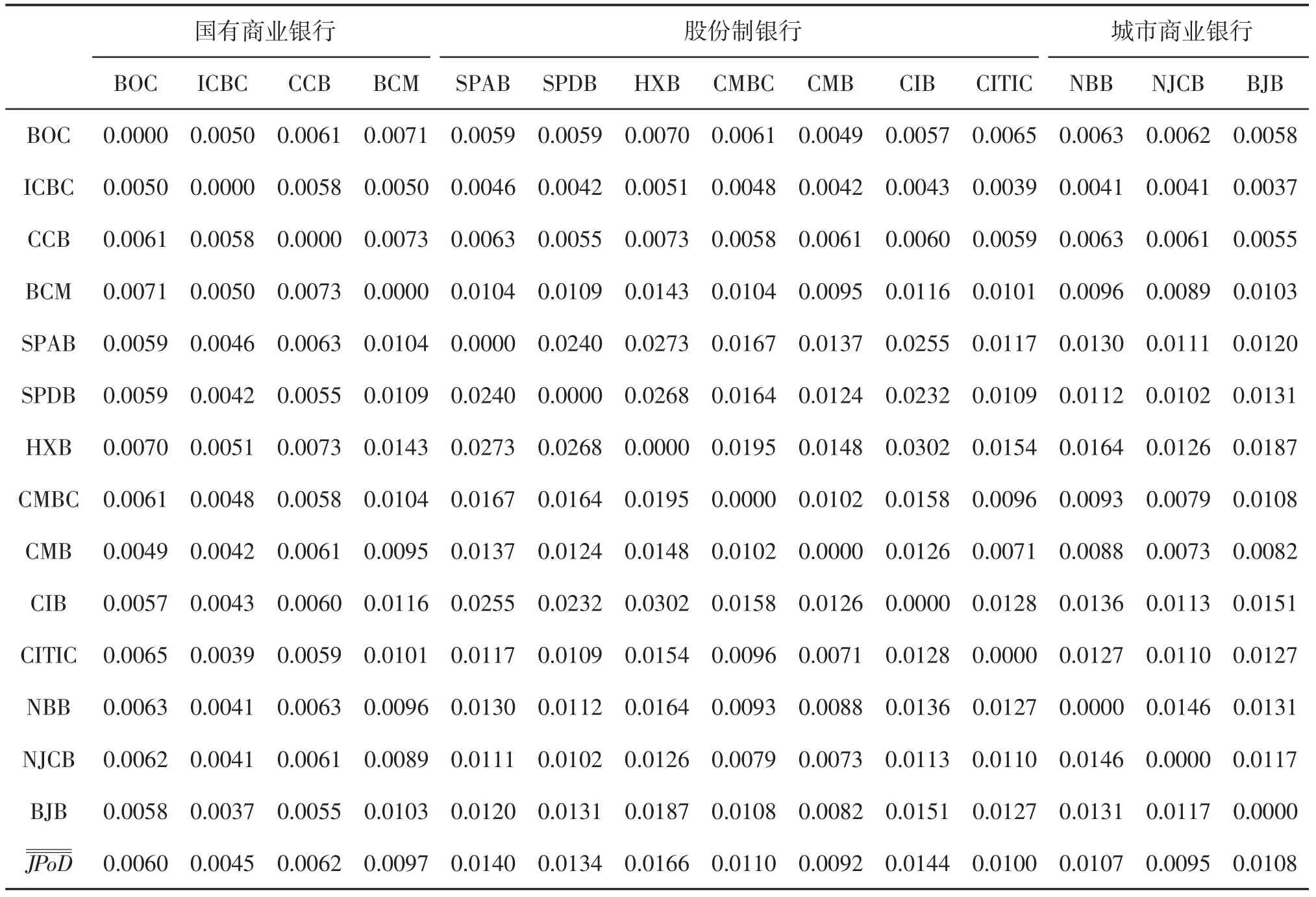
表5 基于Gumbel-Copula的全样本期间联合违约概率

由表5可知，全样本计算的期间联合违约概率中，国有商业银行的平均水平是最小的，最大的也仅为0.0097，说明国有商业银行的违约风险较低，风险缓释能力强，在风险爆发的情况下较少会发生联合违约，基于联合违约概率的风险度量，可以认为国有商业银行是银行业稳定的“阻尼器”。三家城市商业银行的平均联合违约概率处在三种类型银行的中间水平，比国有商业银行稍高，但小于大部分股份制银行，说明在全样本时期的平均水平下，城市商业银行风险传染的能力小于股份制银行。在所有银行中，股份制银行的平均联合违约水平是较高的。股份制银行除了招商银行的平均联合违约概率在0.01以下外，其余的6家股份制银行的平均联合违约概率水平均高于0.01，其中华夏银行的联合违约概率接近0.017。按照期间联合违约率均值度量的信用风险传染，股份制银行在全样本中处于风险传染网络的核心位置，在风险传染中起着较为重要的中心节点作用。因而需要重点关注股份制银行的风险发生水平，重点监管其相应指标，以减少联合违约发生的概率，从而降低系统风险传染水平。

（三）银行系统性信用风险传染效应的网络分析

根据期间联合违约概率矩阵，用阈值法绘制银行信用风险传染的网络结构图。将累积分布概率为0.4水平上的分位数（从大到小第40%个期间联合违约概率值）作为临界阈值，删除低于临界值的边，保留大于等于临界值的边；以期间联合违约概率作为网络拓扑结构的边权重，用网络中边的粗细描述连接边的权重值的相对大小，权重大的边较粗；并以连接到节点的边的数量的多少来区分节点的大小，连接到节点的边的数量越多，节点越大。绘制出的网络图如图1所示。

图1 以联合违约概率度量的风险溢出网络

从图1看出，国有商业银行的连接数最少，中国银行、工商银行和建设银行的连接数为0，这可能是由于国有商业银行有国家资本金做最后担保，发生违约的可能性较小，因而与其他银行的期间联合违约概率也较小，风险传染水平也较低。城市商业银行的连接数也较多，但处在网络的外围，并不是风险溢出网络的中心部分。股份制银行不论是连接数还是网络边的权重数都处在较高的位置，这可能是由于股份制银行追求利润最大化，借贷资本风险较高，发生违约的可能性较大，联合违约概率度量的金融风险溢出水平也较高。从风险的溢出结构来看，需要重点关注处于溢出网络中心位置的股份制银行的潜在风险传染水平，以减少风险溢出传染。

度中心性和介数中心性是衡量网络结构的主要指标。度中心性用节点的连接数量来衡量，一个节点的连接度越大，说明该节点与网络的关联性越强，越处于风险传染网络的中心；介数中心性以最短路径中通过节点的路径数来表示，表示的是节点充当“关联桥梁”的作用能力，介数中心性指标值越大，在网络拓扑结构中的中介作用越强，风险传递的能力也就较强。利用全样本构造出网络传染矩阵，得出上述两个指标的描述性统计，结果如表6所示。

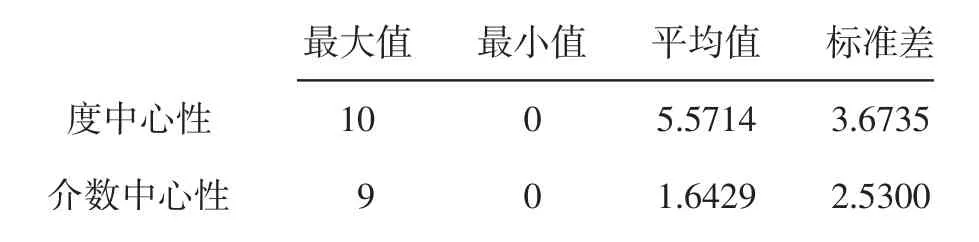
表6 信用风险传染网络结构特征的描述性统计

由表6可知，度中心性最大值为10，说明该银行与其他银行的联合违约概率都比较大，因此保留下来的边的数量也较多，在风险溢出网路中占据靠中心的位置；最小值为0，从风险溢出网络图中来看，连接数为0的点是三家国有商业银行；平均连接数和所选择的阈值有关，此处意义不大。介数中心性以最短路径中通过节点的路径数来表示，最大值为9，说明该银行充当传染桥梁的次数较高，在风险溢出网络中有较强的经纪中介能力，风险发生时容易通过该点传递到其他的节点中；最小值为0，这是由于阈值的确定使得三家银行没有和网络相连接，没有风险传递，此处的银行机构比较安全；平均值为1.64，表明每个节点上通过的最短路径数为1.64条。

（四）银行系统性信用风险传染效应的时序结果与分析

以三个月的交易天数为窗口长度，计算出每个窗口的银行联合违约概率的均值，得到以季度计算的风险传染度量指标，即期间联合违约概率。样本时间从2007年第四季度至2020年第三季度，共计52个季度数据。用计算出的系统性风险传染效应时序数据绘制趋势图，如图2所示。

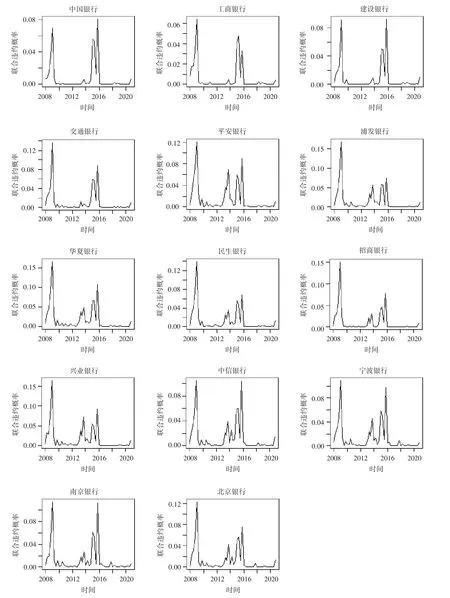
图2 各银行的风险传染指标时序

由图2可知，各银行的期间联合违约概率均值在2008—2010年和2015—2016年期间都有明显提高。在2012年之后的一段时间里，部分银行期间联合违约概率均值也有小幅提高，这与2008年的金融危机、2012的欧债危机和2015年的中国股市危机在时间节点上还是比较符合的。因此，该指标在一定程度上可以作为衡量系统性风险传染效应大小的指标。从2020年第三季度每家银行的期间联合违约概率均值都开始上升，说明银行之间的信用风险传染水平在经历新冠肺炎疫情这一重大公共事件冲击之后有所提升，因而需要采取相应的措施以抑制风险传染水平，保持金融系统的稳定性，提高市场应对疫情负面冲击的能力。

五、银行系统性信用风险传染效应的影响因素实证研究结果与分析

要守住不发生系统性金融风险的底线，只有把握系统性风险传染的影响因素，才能精准调控。本文进一步从银行信用质量特征、银行关联网络和宏观经济环境三个层面，选取期间联合违约概率均值的潜在影响因素，构造普通面板回归模型，验证相关因素对系统性风险传染的影响。

（一）变量选择

参考相关文献，本文从银行信用质量特征、银行关联网络和宏观经济环境三个层次选取传染因素变量，变量选择如表7所示。

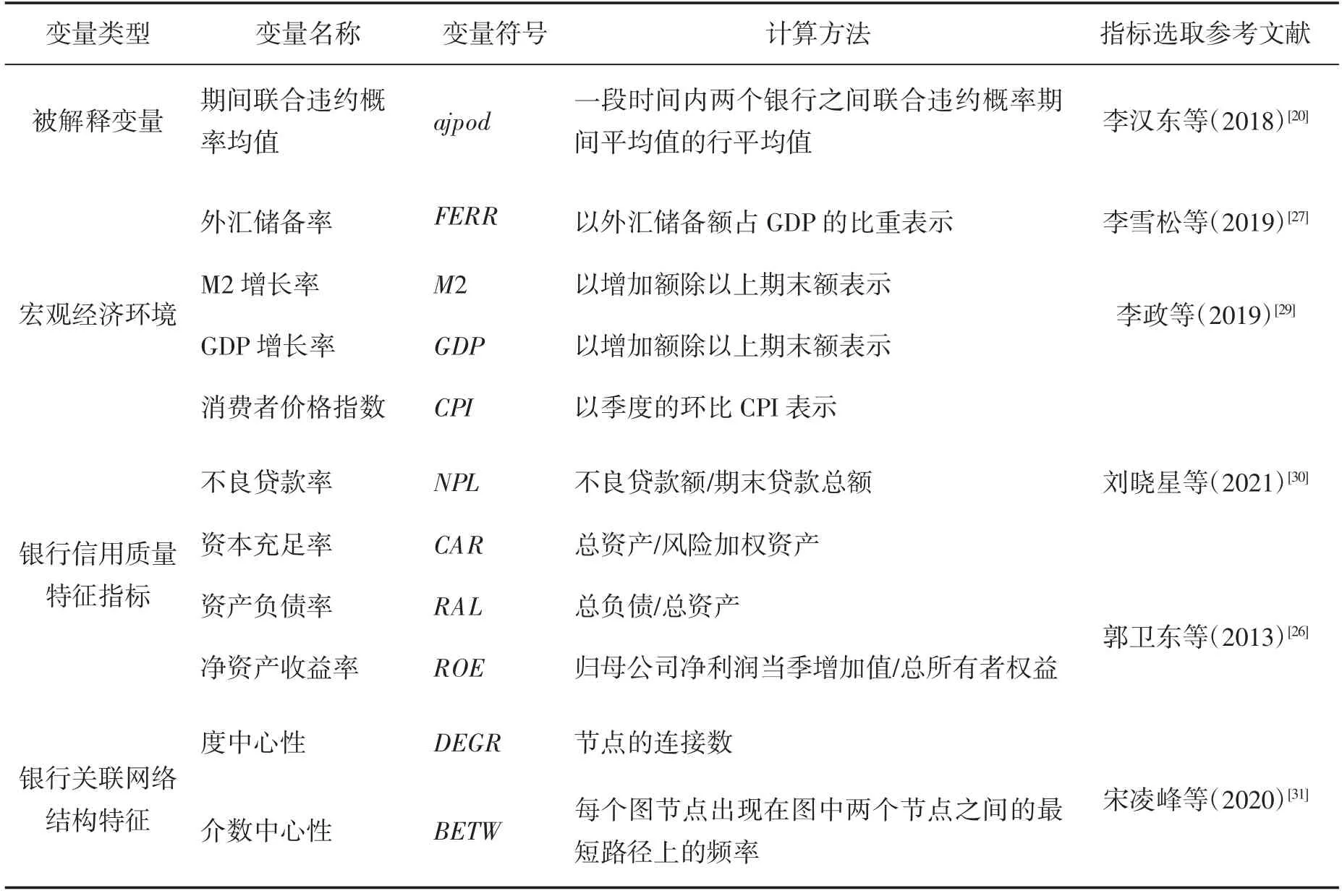
表7 变量的选择和描述

银行指标数据均来自银行公布的定期报告，国际经济数据和宏观经济数据来自WIND数据库和国家统计局网站。样本期间选择2017年第四季度至2020年第三季度，由于部分银行的季报数据不完整，缺失部分用线性插值法补齐。

（二）数据特征检验

为避免出现伪回归情况，本文用LLC检验和IPS检验进行数据平稳性检验，两个检验的原假设都存在单位根，即变量是不平稳的。最优滞后阶数均由AIC准则确定。检验结果表明，上述每个变量至少可以通过一个稳定性检验，所有变量都具平稳性，可以进行后续的方差、协方差检验和个体效应检验。

对全部银行及国有商业银行、股份制银行和城市商业银行三类，分别进行方差、协方差检验，以判断需要选取的模型形式。从检验结果来看，总样本要选择的是变截距模型，说明各银行间的风险传染效应均值差异比较明显；国有商业银行和城市商业银行的各分组样本均需要选择不变系数模型，说明组内的共性还是比较高的；股份制银行需要选择变截矩模型，说明股份制银行组内还存在差异，但总体上同种性质的银行之间比较相似，不同组之间的银行差距比较大。

选择好模型之后，要进行个体效应的Hausman检验和F检验。检验结果表明，全样本模型要选择个体随机效应的变截距模型；国有商业银行和城市商业银行需要选择个体随机效应的不变系数模型；股份制银行要选择个体随机效应的变截矩模型。

（三）银行系统性信用风险传染效应影响因素的全样本验证结果与分析

为验证潜在风险传染因素的实际作用，本文设定的面板数据模型一般形式为：

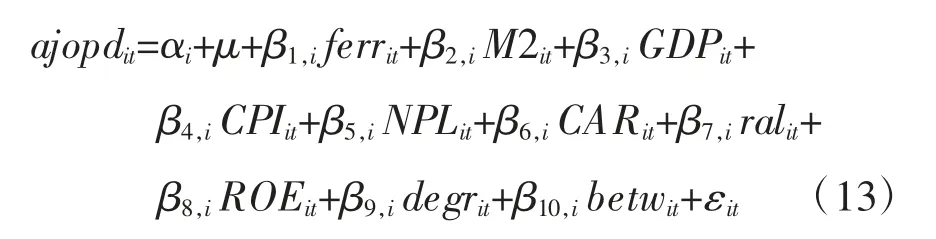
其中，α为常数项个体效应；μ为常数项的均值；β为各变量参数。当不同个体的估计系数和常数项系数都相等时，模型为混合回归模型；当估计系数相同而常数项不同时，模型为变截矩模型；当常数项和各变量的系数均不相同时，模型为变系数模型。

根据方差、协方差检验和个体效应检验的结果选择相应的合适模型，并进行参数估计。估计结果如表8所示。

由表8可知，从全样本回归结果看，外汇储备率（FERR）的回归系数值显著为正，这说明在强制结售汇制度下，国家会提高外汇储备水平，增加国内货币供给，造成经济过热和资产价格泡沫，导致风险传染扩大；广义货币增长率（M2）的系数估计值显著为负，说明适度提高货币发行量，增加金融体系流动性，能够降低系统性信用风险传染水平。国内生产总值增长率（GDP）和价格指数（CPI）的系数估计值显著为负，这表明经济增长相对放缓，通货膨胀水平降低，会增加银行业联合违约概率，提高风险传染水平。

不良贷款率（NPL）测度了银行已有风险承担水平，其系数估计值显著为正，说明高风险承担的银行不仅自身脆弱性较大，而且会在风险传染网络中产生较大负面冲击的风险传染。资本充足率（CAR）是总资产与风险加权资产的比率，资本充足率高，说明银行有较多闲置资金，没有转换成生息资产或投资。资本充足率的估计系数显著为正，说明尽管银行拥有了较高的风险缓释能力，但其资产盈利性较弱，会导致其自身信用质量恶化与联合违约概率提升。资产负债率（RAL）是用总负债除以总资产，因而资产负债率越高表示负债的水平越高，资产负债率的回归系数显著为正，说明负债水平的提高会使得违约概率提高，以联合违约概率度量的风险传染程度也有所增加。净资产收益率（ROE）的估计系数显著为负，说明在净资产收益率较高时，银行自身违约风险较低，其风险传染的能力也会比较低。

从网络结构指标度中心性和介数中心性来看，度中心性（DEGR）的估计系数显著为正，且数值较大，说明银行在网络中所处的位置越在中心，其风险传染路径越多，传染能力也就倍数增强，属于净溢出机构。而介数中心性越高说明该网络节点“中介性”作用越强，介数中心性（BETW）的估计系数显著为负，但数值较小，说明在网络中起到“中介”作用的节点并不是风险传染的最主要角色。

（四）银行系统性信用风险传染效应影响因素的分类实证结果与分析

分类分组回归的结果如表8第3至5列所示。从回归结果来看，除了资产负债率（RAL）系数全部变得不显著之外，系数的正负和显著性水平没有太明显的变化，但在数值的大小方面组别间存在差异。外汇储备率（FERR）对国有商业银行和股份制银行联合违约概率的正向影响较大，而对城市商业银行的影响较低。广义货币增长率（M2）和国内生产总值增长率（GDP）对国有商业银行和股份制银行联合违约概率的负向影响相近，而对城市商业银行的负向影响更大，说明以这两种方式控制风险传染水平时，城市商业银行更容易降低风险传染的程度。消费者价格指数（CPI）对国有商业银行的负向影响较其他两类银行而言更小，说明在物价水平上升时，国有商业银行的联合违约概率下降的程度也较其他两类银行要小一些。

表8 全部银行和银行各组的面板回归结果

不良贷款率（NPL）对三类银行联合违约概率的影响差距较大，对国有商业银行而言，不良贷款率的上升对风险传染水平的提高影响最大，股份制银行次之，城市商业银行最小。这可能是由资产规模不同引起的，国有商业银行资产规模比股份制银行和城市商业银行大，不良贷款率的较小上升会带来不良贷款金额的大幅提高，引起较大的对外影响，风险传染水平也更容易受到影响。资本充足率（CAR）对国有商业银行联合违约概率的影响最高，对股份制银行的影响最小，原因除资产规模之外，还和股份制银行对风险加权资产的计提较高有关，一般银行的资本充足率水平始终在较高水平，风险时期和平常时期的变动较小，因此影响程度也就较小。资产负债率（RAL）在分组之后的各组回归中都不显著，可能是由于负债水平的提高并不能有效影响到联合违约风险的提高；全样本时显著而分组之后不显著，可能是由于样本量的减少导致。净资产收益率（ROE）对国有商业银行的负向影响最大，对股份制银行的影响最小，理由与资本充足率（CAR）的影响相类似，股份制银行的资产回报率一般较高，增加1单位的资产回报率产生的对应变动比较小，因此所造成的负向影响会比其他类型的银行更小，风险传染水平的变动也就更小。

从不同类型银行网络结构化指标的估计系数来看，度中心性和介数中心性的估计系数都存在较大差异。其中，国有商业银行和股份制银行的度中心性（DEGR）估计系数仍然显著，但对于城市商业银行却变得不显著了，说明对于城市商业银行而言，节点的连接数量变化对于风险传染水平的提高与降低没有显著的影响。从参数估计值的大小来看，连接节点的数量对股份制银行的风险传染水平影响更大，与以全部样本估计出的度中心性系数相接近。对于介数中心性（BETW）而言，对国有商业银行和股份制银行的估计系数依然显著，但对城市商业银行风险传染水平的变化没有明显影响。对于国有商业银行和股份制银行而言，虽然介数中心性（BETW）的系数是显著的，但相较于度中心性（DEGR）的指标大小而言，其取值差距较大，因而在条件有限的情况下，要更关注网络中连接数量较多的节点而不是“中介”作用较强的节点。

六、研究结论与政策启示

系统性风险的核心特征在于信用风险传染。本文利用KMV模型估算了样本银行的预期违约概率序列，拟合其边缘概率分布函数，并用Copula函数得出任意两家银行间的联合违约概率，用其均值测度银行信用风险传染，构建起风险传染网络。为了精准防控系统性风险传染，准确识别其影响因素，本文通过构建面板数据模型，验证了期间联合违约概率均值在宏观、网络与银行三个层面上的影响因素。可以得到以下研究结论：

第一，关于影响因素。实证结果表明，从全样本回归来看，银行不良贷款率、银行资产负债率、银行资本充足率、宏观外汇储备率和银行网络中心度对联合违约概率具有显著正向作用，影响力度依次减弱。CPI、净资产收益率、M2、国内生产总值和银行介数中心性对联合违约概率具有显著的负向影响，影响力度依次减弱。

第二，关于传染效应。银行风险传染影响因素的分类面板回归结果显示，多数因素影响的显著性和正负性与全样本基本一致，只是在作用力度上具有异质性。关于宏观外汇储备率和货币政策的影响，银行分类分析和全样本分析结果基本相同。而国内生产总值对城市商业银行的影响力度较大；CPI对国有商业银行的影响较弱些；银行不良贷款率对国有商业银行和股份制银行有显著的正向影响，而对城市商业银行不显著；资本充足率对国有银行和城市商业银行的影响较显著，而对股份制银行不显著；资产负债率的影响在分组之后变得不显著了。从网络结构因素看，度中心性对国有商业银行和股份制银行具有显著的正向影响；而介数中心性对国有商业银行和股份制银行具有显著的负向影响。

由本文结论，可以得到以下政策启示：

第一，应继续深化完善货币政策和审慎监管政策相互协调配合的“双支柱”调控框架。外汇储备率对所有银行的风险传染都具有显著正向影响，外汇储备政策调整要兼顾保持币值稳定、调节国际收支和维护金融稳定三重目标。短期内货币供给增加会直接使经济体系中的流动性宽裕，抑制银行风险传染，但同时会增加资产泡沫，提高经济杠杆率，增加存量风险承担。货币政策调控要同时兼顾金融和实体经济双稳定目标。要厘清不同政策工具在经济调控和风险防控两个领域的作用方向、机理、方式和适用条件，探索双支柱调控下的政策协调机制。

第二，健全跨周期监测调控体系。经济增长率和CPI对系统性风险传染具有显著负向作用，这样，在金融个体风险顺周期性的基础上，增加了金融传染风险的顺周期性，双重顺周期性叠加会增强系统性风险的顺周期性，因此跨周期审慎监管挂钩指标与资本缓释措施应当覆盖金融体系的自身风险和传染风险。

第三，继续完善微观审慎监管。银行自身特征指标对银行风险传染都有显著影响，微观金融安全是宏观金融稳定的基础与前提。守住不发生系统性风险底线的基础还在于微观金融安全，在完善双支柱调控框架的同时，还要继续加强微观审慎监管，完善压力测试和监测预警机制，充分发挥宏观审慎结构性调控监管作用。

第四，建立系统重要性审慎监管体系。处于关联中心地位的金融机构对系统性风险传染具有显著正向作用，防控系统性风险的一个重点就是系统重要性机构监管，合理设置系统重要性附加资本监管。另外，要建立全覆盖的金融风险监测预警体系，重点加强对流动性紧缺、加杠杆、债务和金融周期的监测，把有系统重要性影响的因素、机构、市场和设施都纳入宏观审慎管理。