新型安全壳热压耦合分析
2022-10-16徐文胜童元申张昆桥
王 振, 徐文胜, 童元申, 张昆桥, 罗 辉
(1. 中核武汉核电运行技术股份有限公司, 湖北 武汉 430074;2. 武汉华中科大检测科技有限公司, 湖北 武汉 430074;3. 华中科技大学 土木与水利工程学院, 湖北 武汉 430074)
随着社会发展和科技进步,人类日益增长的能源需求与传统不可再生能源逐渐枯竭之间的矛盾愈发严重,核电则是未来我国能源结构调整的最佳选择。核电站设置有三道实体屏障,阻止放射性物质向环境释放,由内到外分别是:燃料芯块和包壳、压力容器和密闭的一回路系统、安全壳[1]。安全壳作为保证核电站安全的最后一道实体屏障,其安全性一直备受设计人员关注。
陈勤[2]与孙锋[3]等分别利用 ANSYS 建立预应力混凝土安全壳模型,发现在设计内压下,安全壳仍处于弹性状态,满足正常使用要求,筒身先于穹顶发生塑性变形。赵超超等[4]利用 ABAQUS建立 CPR1000核电站安全壳整体式模型,发现安全壳安全性主要由设备闸门区域控制,故建议通过提高预应力钢筋等级、增加闸门洞口附近配筋率等措施提高其承载能力。薛荣军等[5]利用 ABAQUS 软件进行精细化建模,对某安全壳在超设计内压下力学性能进行研究,发现在设计内压下,安全壳整体处于弹性阶段,满足正常使用要求。随着内压荷载增大,钢衬里、钢筋和预应力钢束依次屈服,混凝土裂缝首先开始于设备洞口附近而未发展贯穿,第一条竖向裂缝出现于筒壁中部内侧,穹顶裂缝在筒身近乎破坏时才开始出现,并沿穹顶筒身交界处向穹顶顶部发展。Ahmad Shokoohfar等[6]在考虑钢衬里、贯穿件等细节的基础上,对PCCV(Precooler Control Valve)在温度与内压荷载共同作用下的热学与力学性能进行分析,并将试验结果与仿真结果进行对比。结果发现,温度以及低预应力值筋对 PCCV 的极限承载能力影响不大,而受钢衬里刚度或强度不连续性的影响很大。
目前核电站采用的第三代预应力安全壳主要为双层安全壳,内层为预应力结构,外层为钢筋混凝土结构。相比于单层安全壳,双层安全壳中的外层不仅可起到抵抗爆炸冲击、飞机撞击等荷载的作用,而且可在发生失水事故时有效屏蔽核辐射,保证安全壳周围人员不受超剂量核辐射影响,但对内层抵抗内压荷载没有太多有利帮助,因此本文选取国内新一代自研安全壳内层作为研究对象,对其内压与温度耦合作用下工作性能进行研究。
1 安全壳有限元模型
1.1 几何模型建立
新型安全壳由半球型穹顶、筒身、筏板基础、扶壁柱、钢衬里、预应力钢束、普通钢筋等部分组成,如图1所示,与前两代安全壳不同的是将扁穹顶改为半球顶,与筒身之间不设环梁,几何形状连接更加平滑。筒身扶壁柱也减少到两根,从100°方向处基础底面起始通过穹顶顶部延申至280°方向处基础底面,受力更加合理。
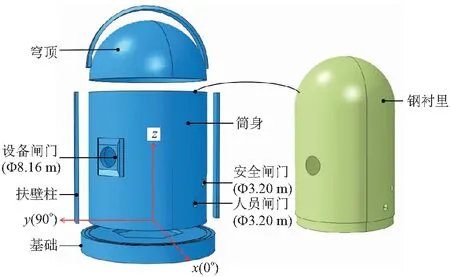
图1 新型安全壳内层组成
如剖面图2所示,安全壳基础底标高-14.900 m,穹顶顶部标高+69.580 m;筒身内径23.400 m,外径24.700 m,厚度为1.3 m,穹顶厚度为1.05 m,钢衬里厚度为6 mm。安全壳除基础采用C40混凝土外,其余均采用C60混凝土。此外在筒身+1.2 m标高334°处设置有直径为3.20 m的人员闸门,+8.7 m标高318.9°处设置有直径为3.20 m的安全应急闸门,+19.7 m标高60°处设置有直径为8.16 m的设备闸门。预应力系统采用法西柰公司的C系列锚固系统,分为环向预应力钢束和倒U形预应力钢束,其中环向预应钢束共计53根,锚固于扶壁柱上;倒U形预应力钢束共计94根,锚固于基础顶部,如图3所示。均采用1860级预应力钢绞线,采用后张法施加预应力。筒身普通钢筋共计分为内、中、外三层,每层又分有环向钢筋和纵向钢筋,穹顶分为内外两层,均采用HRB500级,如图4所示。
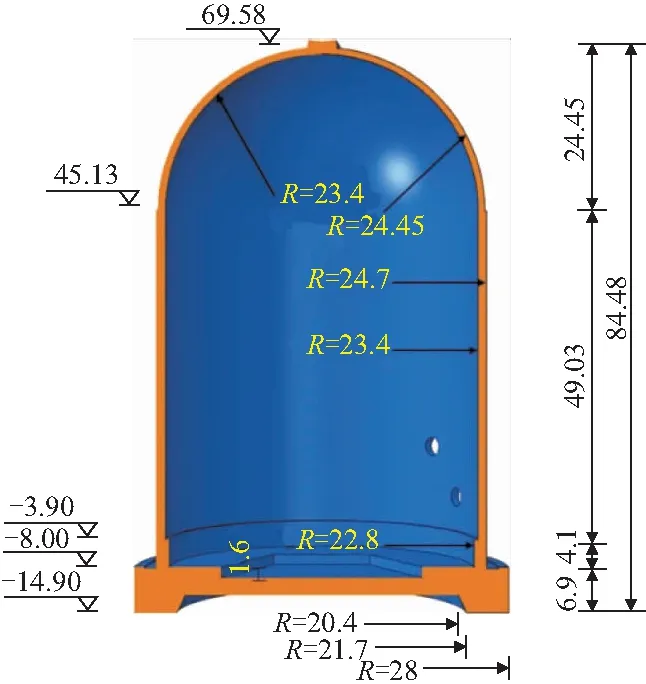
图2 内层混凝土尺寸/m
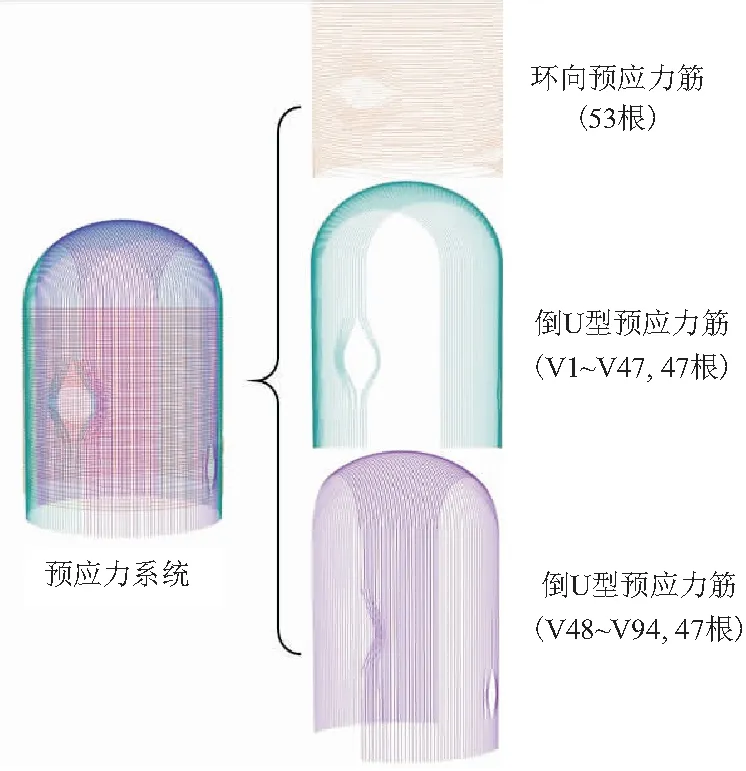
图3 预应力系统组成
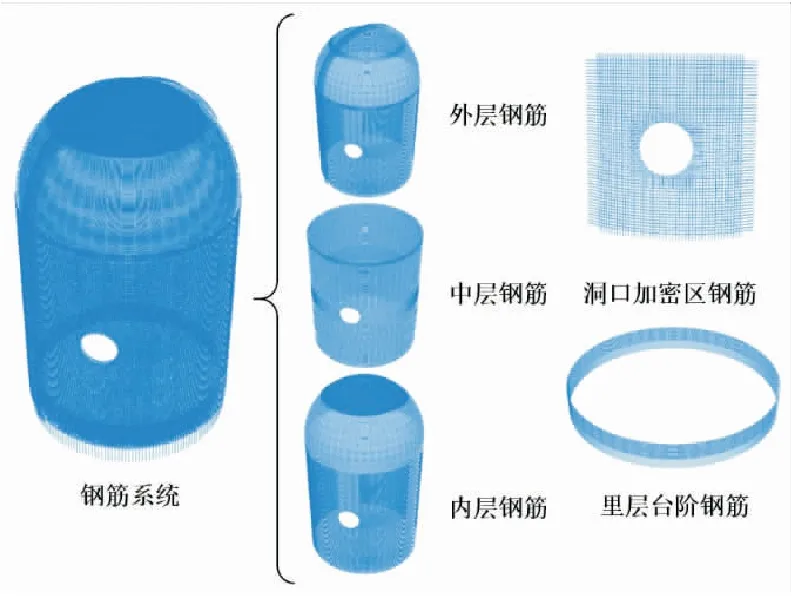
图4 普通钢筋系统组成
1.2 网格无关性检验
利用ABAQUS有限元分析软件建立安全壳有限元仿真模型,生成网格的方法有三种:自由网格法、映射网格法和扫描网格法。根据安全壳结构的特点,采用自由扫掠网格的组合。将混凝土筒身划分为多个规则部分,通过扫掠网格生成六面体网格C3D8R。在穹顶、基础与设备闸门区域,通过自由网格生成四面体网格C3D4,如图5所示。钢衬里采用S4R四结点曲面薄壳单元划分,预应力钢束与普通钢筋均采用T3D2两结点线性三维桁架单元进行划分。
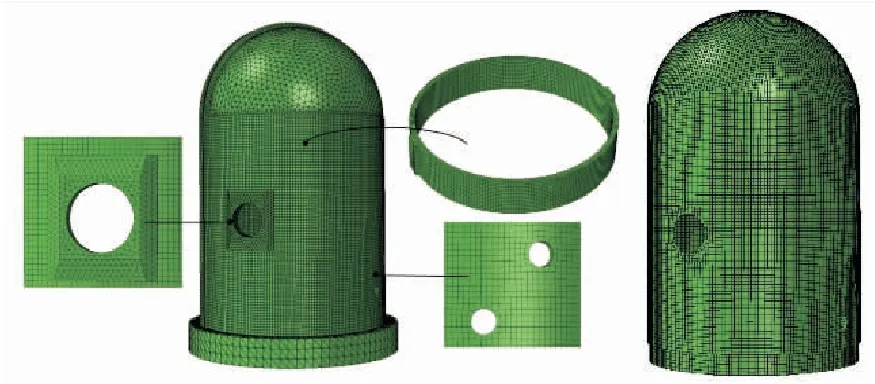
图5 0.65 m基本尺寸混凝土与钢衬里网格
需特别指出的是,ABAQUS软件中有多种钢筋建立方法,例如实体单元法、钢筋面法、复合壳法。实体单元法,即以杆单元建立纵筋与箍筋的钢筋骨架,而后嵌入混凝土实体单元;钢筋面法,即以面单元代表钢筋网,定义单根面积、间距、方向角等多种属性,而后嵌入混凝土实体单元;复合壳法,即将某些特殊的混凝土结构定义为壳单元,将钢筋当作复合材料定义于壳单元中。实体单元法适用于单个构件分析,但对于大型构件建模过程相对复杂;后两种方法用于大型构件建模时相对较为简单,但只能考察主体构件的性能,无法准确考察钢筋性能。鉴于目前针对普通钢筋屈服时刻研究较少且需建立洞口加密区钢筋等原因,本文采用实体单元法模拟普通钢筋如图4所示。对于预应力筋,首先利用Python语言编写各条预应力筋的空间曲线方程,而后导入ABAQUS中形成部件,如图3所示。
选取合适的网格大小是有限元前处理中至关重要的一步,因此本节对新型安全壳网格无关性进行讨论,即研究网格密度变化对计算结果的敏感性影响[7]。为准确表达安全壳几何特性,筒身采用六面体单元,穹顶、基础以及设备闸门洞口位置采用四面体单元,其中基础部分网格基本尺寸采用2 m大小不变。因需考虑内外温差在安全壳内部产生的温度梯度分布,故沿筒身厚度方向分为四层,由内至外尺寸分别为0.35,0.35,0.35,0.25 m;沿穹顶厚度方向分为三层,尺寸均为0.35 m。
沿筒身表面、穹顶表面分别选取0.60,0.65,0.70,0.75,2.0 m五种大小网格进行划分。计算工况为设计内压作用(0.42 MPa),评价指标选取筒身最大位移、混凝土最大拉应力、钢衬里最大拉应力、预应力筋最大拉应力、普通钢筋最大拉应力、综合误差以及计算时长等七项,其单元个数与计算结果分别如表1所示。
根据表1结果显示,相比于0.60 m大小网格,0.65 m的综合误差仅为0.9%,计算时长减小了0.9 h;而0.70 m与0.75 m两类网格计算结果较为接近,但与0.60 m相差较大;2.0 m大小网格计算误差明显,与此同时计算时长显著减小。综上所述,选取0.65 m大小网格能较好平衡计算精度与时长的关系,有利于后续研究计算,如图5所示。
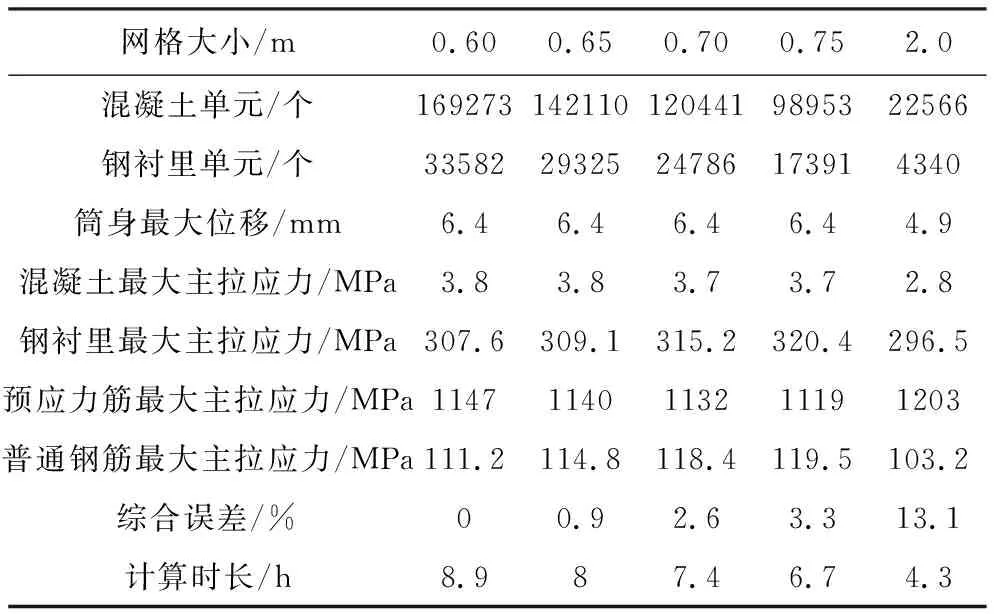
表1 5种网格单元个数与计算结果
1.3 材料属性
混凝土、钢衬里、预应力钢束、普通钢筋等材料仿真参数主要取自于GB 50010—2010《混凝土结构设计规范》(2015版)[8]与GB 50017—2017《钢结构设计标准》[9],混凝土采用塑性损伤模型进行仿真分析,其材料参数如表2所示,钢衬里、预应力钢束、普通钢筋等钢材采用双折线理想弹塑性模型,其材料参数如表3所示。
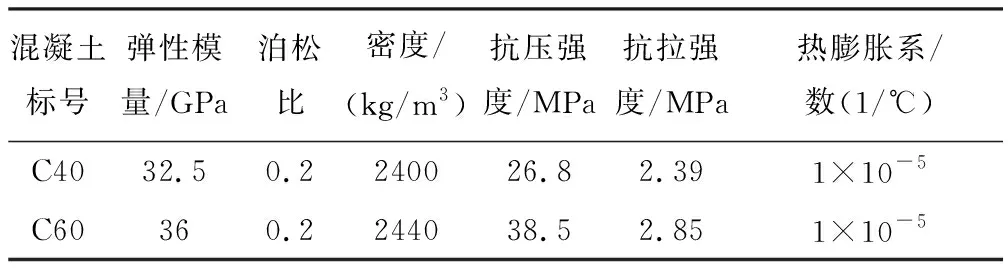
表2 混凝土材料属性
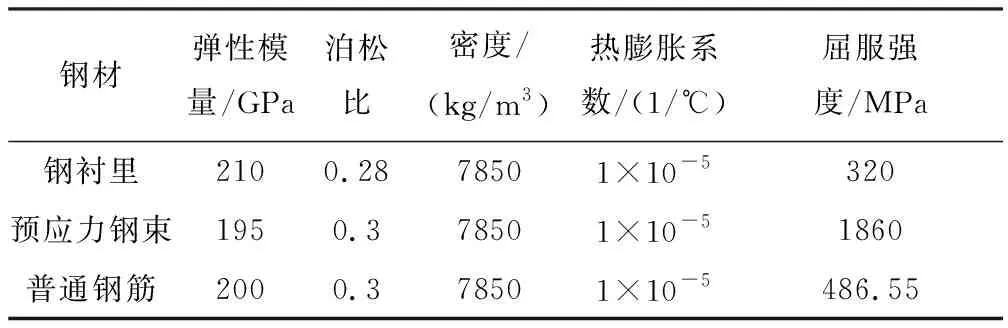
表3 钢材材料属性
2 温度必要性分析
2.1 温度场计算
沿混凝土筒身厚度方向划分尺寸为4个单元,采用基本尺寸为0.65 m的DC3D8和DC3D4传热单元;钢衬里采用基本尺寸为0.65m的DS4和DS3传热壳单元。材料属性方面,混凝土的导热系数采用1.74 mW/(mm·℃),比热为9.7×108mJ/(t·℃),热膨胀系数为1.0×10-5;钢衬里的导热系数采用48 mW/(mm·℃),比热为5.0×108mJ/(t·℃),热膨胀系数为1.0×10-5。分析步采用瞬态热传递分析,内部温度为可能出现的最高温度150 ℃,以温度边界条件形式作用于钢衬里内侧,外部环境温度为20 ℃。为简化仿真计算过程,本文对温度传递做以下假定:
(1)假定安全壳内部反应温度与钢衬里内侧温度一致,不考虑温度源距内测而造成的散热影响,外部环境温度与混凝土外侧温度一致;
(2)假定内部反应温度与外部环境温度为定值,不随内压荷载大小变化;
(3)假定混凝土与钢衬里各项属性指标与温度无关,不随温度大小变化。
筒身安全壳总共被划分为4层,由内至外分别为A,B,C,D,E 5个节点。图6为该5个节点随时间温度变化曲线。由图可知:A点温度通过钢衬里传递迅速升至149 ℃左右,并最终稳定于149.94 ℃;B点临近内壁,起初升温迅速而后因向C点传热导致增速减慢最终稳定于112.47 ℃;C点因位于筒身中部故初始增长最为缓慢,而后因B点温度传递而增速加快,最终稳定于72.65 ℃;D点总体增速最为缓慢,最终稳定于47.03 ℃,整个传递过程持续193 h后进入稳定状态。
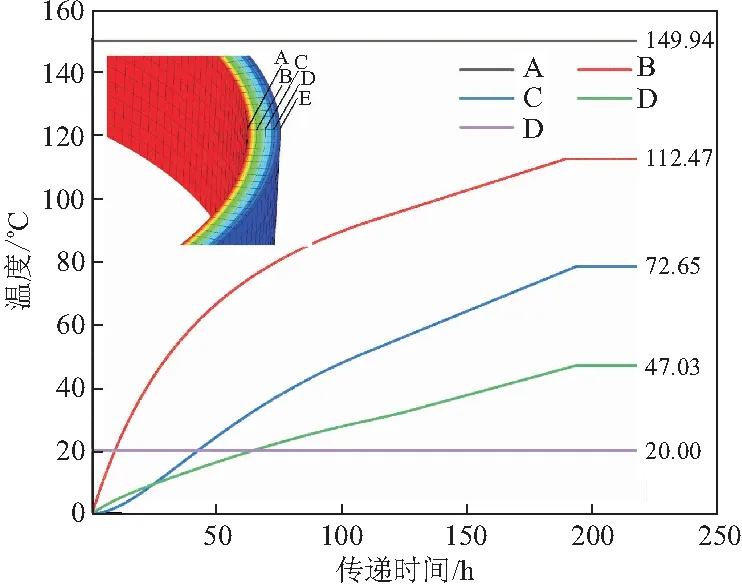
图6 筒身温度变化曲线
图7为筒身温度沿壁厚变化图,由图可以看到稳态时温度沿筒身基本线性分布,安全壳底部台阶处因几何突变,导致局部温度无法扩散而略高于内部反应温度,达到159 ℃左右。而后将温度以预定义场形式施加在内压计算模型中即可得到热力耦合模型,分别对两模型进行计算并对其计算结果进行对比。
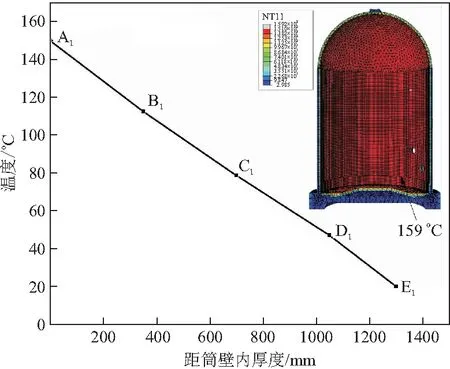
图7 筒身温度沿壁厚变化
2.2 温度必要性分析
本节首先讨论温度对内压荷载的影响,即分别建立两组仿真模型,其中一个施加温度场,一个不施加温度场。内压荷载均由0 MPa开始,以1/10设计内压(0.042 MPa)为荷载步逐步施加内压荷载进行极限承压分析,选取筒身水平位移最大点荷载 - 位移曲线作为评价指标对温度必要性进行分析。因仅考虑内层安全壳承受荷载,而忽略了环形空间内钢结构及外层安全壳的承载能力,故计算结果相对偏安全。
绘制考虑温度和忽略温度两种情况下筒身水平位移最大位置的荷载 - 位移曲线如图8所示。可以发现,考虑温度情况下结构位移变化趋势一致,且在相同内压作用下考虑温度会放大结构变形,尤其是当内压超过1.7倍设计内压,安全壳进入非线性阶段后,放大作用更为明显。未考虑温度效应时安全壳极限内压为2.8倍设计内压,筒身最大位移为556.1 mm;考虑温度效应时安全壳极限内压为2.6倍设计内压,筒身最大位移为479.5 mm。
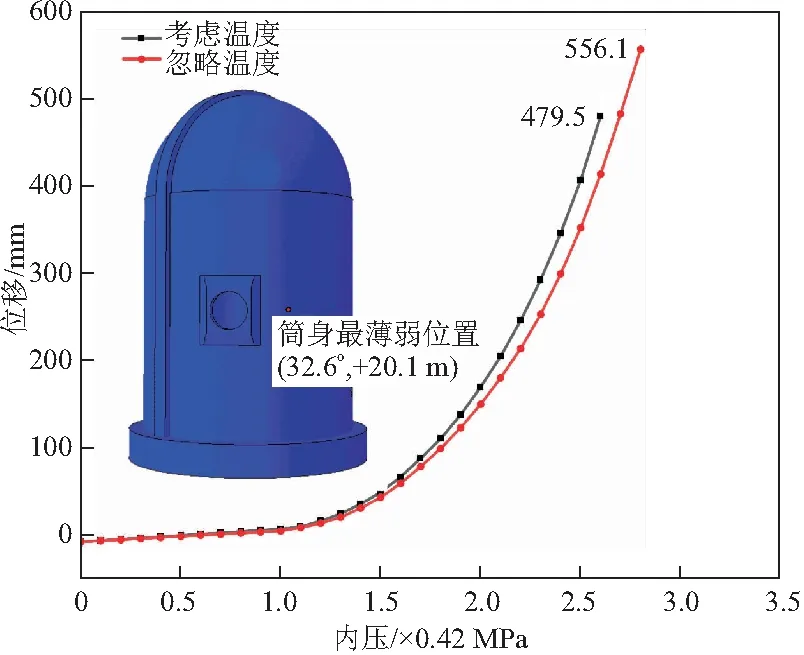
图8 考虑温度与否筒身薄弱位置荷载 - 位移曲线
通过对比可以发现,当核电站安全运行时,温度作用对安全壳的影响并不明显,但当核电站发生事故内压荷载增大时,温度作用便不可忽略。由此说明考虑温度可使计算结果更为保守安全,同时说明考虑温度作用是必要的。
3 热压耦合结果分析
确定核反应附加温度在安全壳内部温度场分布后,将计算所得温度场以预定义场的形式施加在结构上,得到模型的温度应力,而后逐步以1/10设计内压(0.042 MPa)为荷载步逐步施加内压荷载进行计算。
为准确探究热力耦合作用下安全壳结构响应,分别从混凝土荷载 - 位移曲线、钢衬里荷载 - 等效塑性应变曲线、预应力筋荷载 - 应力曲线、普通钢筋荷载 - 应力曲线、安全壳外轮廓图、安全壳薄弱位置等6个方面提取计算结果并进行分析。
3.1 混凝土筒身、穹顶荷载 - 位移曲线分析
图9,10为筒身、穹顶薄弱位置荷载 - 位移曲线,由图可见,在仅施加预应力作用时,安全壳整体处于受压状态,筒身初始位移为-8.3 mm,穹顶位移为-16.1 mm。图9中可以发现,热力耦合作用下安全壳筒身位移状态主要分为三个阶段:第一阶段为a点至b点,即荷载 - 位移曲线为线性阶段,此时混凝土、钢衬里、预应力筋、普通钢筋等均处于弹性状态,b点对应混凝土开始进入塑性屈服阶段,大小为1.1倍设计内压,由此可发现即使在忽略内外层间围护结构及外层安全壳承压作用情况下,安全壳在设计内压作用下仍为弹性状态;第二阶段为b点至e点,混凝土洞口部位出现破坏后,整体刚度下降,洞口部位其余部件承受内压逐渐增加,荷载 - 位移曲线进入非线性阶段,并在图中c,d,e3点处钢衬里、预应力筋、普通钢筋依次进入塑性状态,此时对应荷载分别为1.8,1.9,2.0倍设计内压;第三阶段为e点至f点,在所有部件均进入塑性状态后,安全壳整体刚度大幅降低,随着内压荷载的增加,安全壳急速破坏,直至f点,筒身最大位移为479.5 mm。
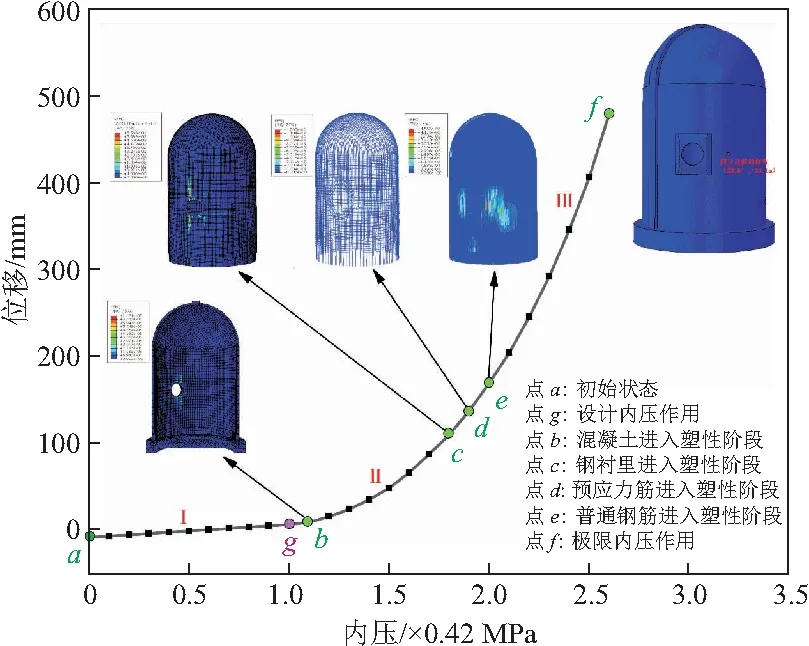
图9 筒身薄弱位置荷载 - 位移曲线
从结构失效角度分析,由钢衬里最大拉应变控制的临界荷载为1.8倍设计内压,由混凝土最大拉应变控制的临界荷载为1.5倍设计内压,由预应力钢筋屈服控制的临界荷载为2.1倍设计内压,由普通钢筋应变控制的临界荷载为2.2倍设计内压。因此,保证安全壳功能完好的极限内压为1.5倍设计内压,保证安全壳结构完整的极限内压为2.1倍设计内压。
结合图10可以发现,穹顶荷载 - 位移曲线的线性阶段远大于筒身部分,直至1.8倍设计内压才逐渐进入非线性阶段,一旦进入非线性阶段,位移曲线急速增加直至f点结构破坏,穹顶最大位移为349.5 mm,即安全壳筒身的破坏导致穹顶位移突增,而非穹顶本身破坏。且圆壁柱的设置有效限制了安全壳穹顶变形,最大位移区域位于圆壁柱两侧。
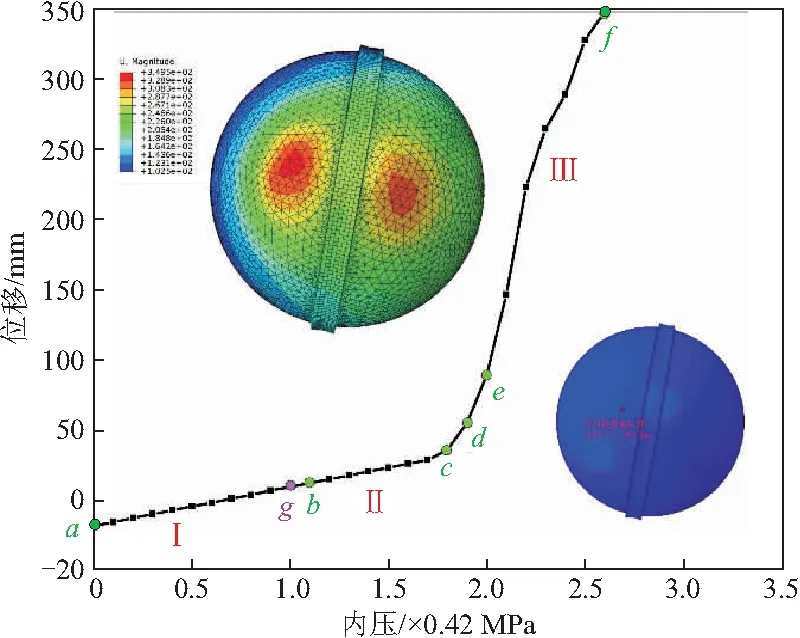
图10 穹顶薄弱位置荷载 - 位移曲线
3.2 钢衬里等效塑性应变分析
图11给出了5个不同位置点的荷载 - 等效塑性应变曲线以及极限内压下钢衬里的等效塑性应变图,可以发现当内压荷载达到1.8倍设计内压,即0.756 MPa时,设备洞口处钢衬里首先屈服(S1点),洞口刚度明显降低,屈服迹线迅速沿筒身竖向发展;而后洞口右侧(S2点)出现水平向屈服迹线,发展也较为迅速;紧接着人员洞口与应急洞口之间(S4点)出现连通屈服迹线,起初发展较为缓慢,但当荷载达到2.3倍设计内压后,屈服速度明显加快;而后应急闸门与设备闸门之间(S3点)先后出现多条竖向迹线,与此同时钢衬里与混凝土基础台阶接触处出现环向屈服迹线(S5点)。此外通过对钢衬里的整体分析可以发现,温度内压耦合作用下钢衬里的主要屈服位置位于应急闸门与设备闸门之间,即318.9°~60°范围内,而80°~300°范围内基本未进入塑性阶段。

图11 钢衬里荷载 - 等效塑性应变曲线
3.3 预应力筋荷载 - 应力曲线分析
在环向预应力筋和倒U型预应力筋中分别选取3个位置点,绘制其荷载 - Mises应力曲线,并分别给出极限内压下两类预应力筋的Mises应力图,如图12所示。可以发现,当荷载小于1.7倍设计内压(0.714 MPa)时,除洞口位置环向预应力筋外,其余钢筋Mises应力值变化均不大。此外,设备闸门洞口处(M1点)环向预应力筋应力值率先开始增长,并于1.9倍设计内压(0.798 MPa)时达到1860 MPa进入屈服阶段,而同一位置(M4点)倒U型预应力筋于2.5倍设计内压(1.05 MPa)时屈服。总体而言,环向预应力筋承担主要荷载,而倒U型预应力筋主要在环向筋接近屈服或已屈服时受力增大,且Mises应力增长迅速。此外,可以发现即使在极限内压作用下穹顶部分预应力筋也未屈服,Mises应力值主要集中于1400~1500 MPa之间,应力较大位置主要位于圆壁柱两侧。
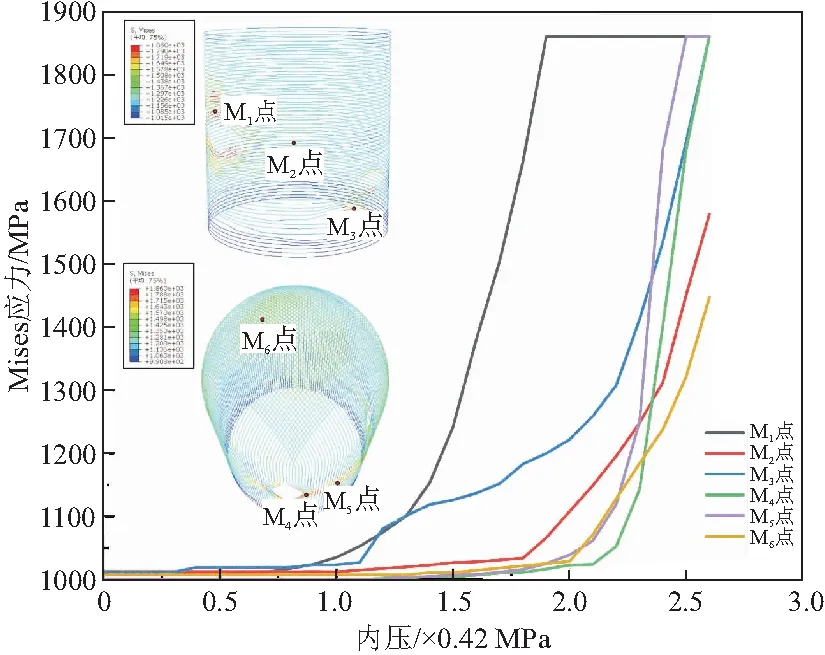
图12 预应力筋荷载 - Mises应力曲线
3.4 普通钢筋荷载 - 应力曲线分析
从外层普通钢筋中分别选取具有代表性4个位置点,分别位于筒身薄弱部位(N1点)、筒身与穹顶连接处(N2点)以及穹顶应力偏大处(N3点)、筒身与基础连接处(N4点),绘制其荷载 - Mises应力曲线,并给出在0.42,0.84,1.092 MPa作用下普通钢筋的Mises应力图,如图13所示。可以发现普通钢筋与预应力筋的变化规律基本一致,其主要屈服部位主要集中在洞口右侧以及扶壁柱与圆壁柱连接部位,0.42 MPa内压荷载作用下普通钢筋Mises应力主要在5~30 MPa范围内,而当荷载达到0.84 MPa时,洞口部分钢筋已屈服一部分,与此同时部分筒身与穹顶连接处、筒身与基础连接处应力快速增长,并最终于1.092 MPa内压时达到屈服应力,随后结构失效。此外,穹顶部分钢筋始终未发生屈服,最大应力为415.7 MPa。
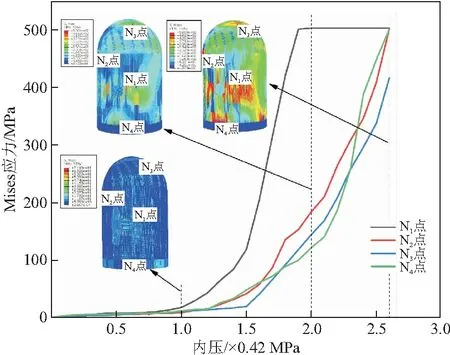
图13 普通钢筋荷载 - Mises应力曲线
3.5 安全壳外轮廓水平位移曲线
图14中给出了变形放大500倍时0.42 MPa作用下安全壳的部分外轮廓水平位移曲线,即在原外轮廓坐标基础上增加水平位移绘制而成,竖向位移暂不考虑,通过图14a可以发现设备闸门左右两侧有明显的外膨胀趋势,而在闸门本身所在位置出现内凹变形,且左侧由于扶壁柱的存在,变形受到限制小于右侧,同时另一侧扶壁柱也有效限制了变形。通过图14b可以发现,20.1°所在外轮廓线在+20 m左右高度明显外凸;60°轮廓线随之也呈现中部外凸趋势,但在+18~+30 m范围内变形较为一致;而以190°轮廓线为代表的未出现洞口一侧在整个筒身范围内变形均较为一致,相差不大。
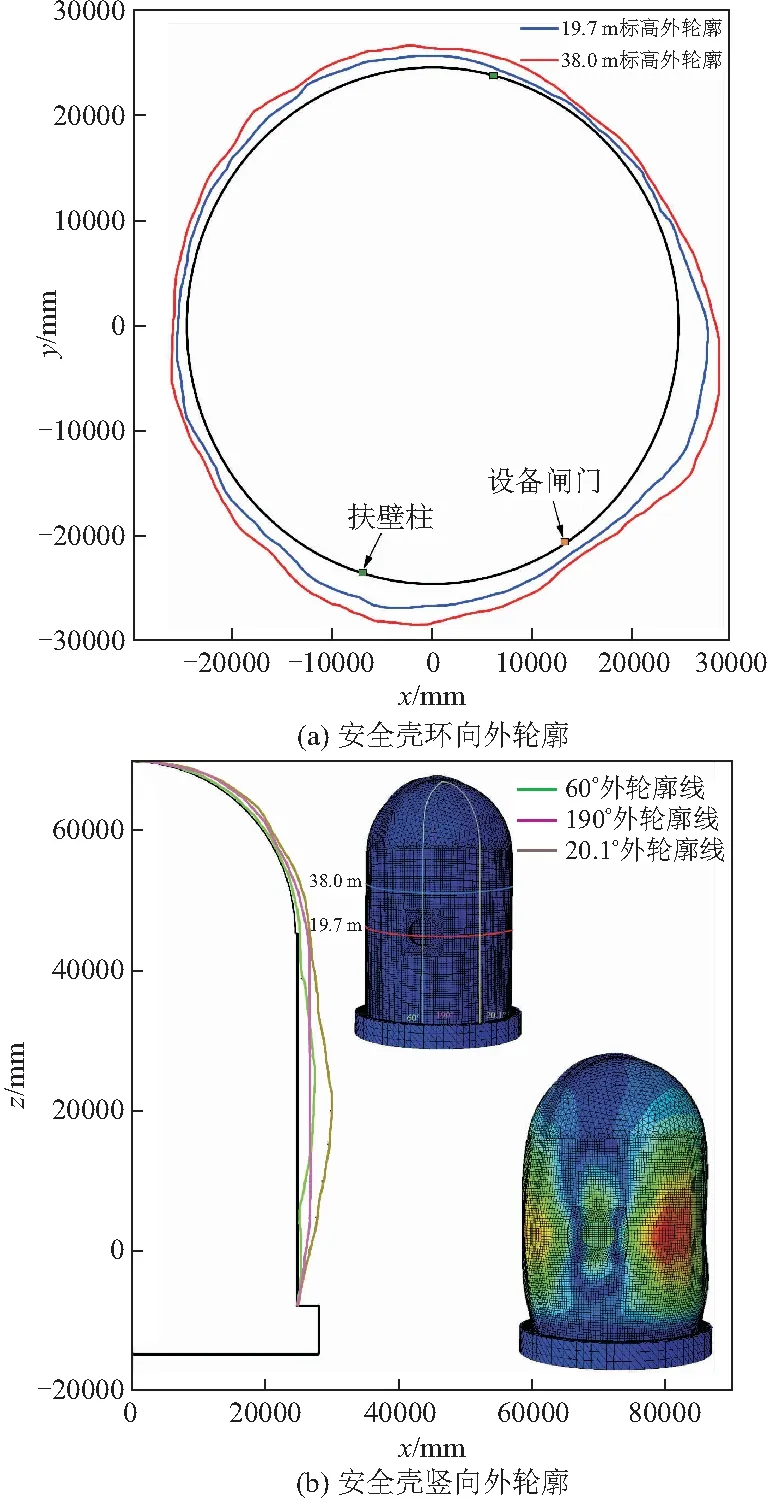
图14 0.42 MPa作用下安全壳外轮廓水平位移曲线(放大比例:1∶500)
3.6 安全壳薄弱位置分析
设备闸门开洞导致应力集中,因此即便在考虑部分钢筋加密的情况下,裂缝仍最先开展于内凹的上下侧(如图15中①处),并沿竖直向基础与穹顶部位延伸;而后一条裂缝由洞口右侧向外扩展(如图15中②处),左侧由于扶壁柱的存在并未出现明显水平裂缝,而是分别沿扶壁柱形成两条损伤迹线(如图15中④处);最后由于人员闸门与备用闸门相距较近而形成一条贯通裂缝(如图15中③处)。因此安全壳在温差内压耦合作用下最薄弱部位仍在设备闸门上下侧,这与2002年Michael F. Hessheimer进行的1/4预应力安全壳缩尺模型破坏情况类似(图16[10])。此外还可以发现:安全壳筒身裂缝总是由内壁起始扩散至外侧,且直至安全壳破坏穹顶仍未出现裂缝,仅少许损伤点。
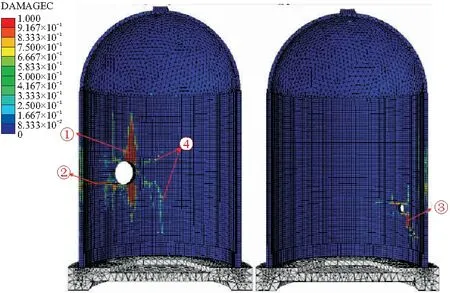
图15 极限内压作用下安全壳受压损伤

图16 1/4缩尺模型破坏模式
4 总 结
本文针对某新型核电站安全壳结构性能的尚不明确问题,基于ABAQUS通用有限元软件,采用三维空间编程建模技术与分离式建模方法,建立包含两类复杂三维空间预应力筋与多层普通钢筋的精细化有限元仿真模型。并对其在内压与温度耦合作用下的结构特性进行研究,主要结论如下:
(1)即使忽略外层安全壳以及环形空间内钢结构,无内压荷载作用下安全壳整体处于受压状态,设计内压作用下安全壳仍处于弹性状态,随着内压荷载的增加,混凝土、钢衬里、预应力筋、普通钢筋依次进入塑性阶段,保证安全壳功能完好的极限内压为设计内压的1.5倍,保证安全壳结构完整的极限内压为设计内压的2.1倍;
(2)安全壳筒身径向位移基本呈现三段式:线性阶段、非线性阶段、破坏阶段,筒身在设计内压、功能完好极限内压、结构完整极限内压作用下最大位移为6.4,48.4,204.3 mm,穹顶在设计内压、功能完好极限内压、结构完整极限内压作用下最大位移为9.9,23.3,147.4 mm;
(3)设备闸门的存在极大增加左右两侧安全壳的径向位移,上下两侧呈现内凹状态,扶壁柱与圆壁柱的设置则有效限制局部安全壳的变形;
(4)安全壳最薄弱位置仍位于筒身设备闸门附近,而穹顶未出现明显损伤,与美国Sandia实验室缩尺模型试验结果相似,建议进一步加强各闸门洞口部位,以延缓其破坏时间;
(5)在仅考虑受力合理情况下建议将人员闸门与应急闸门分开布置,且与设备闸门分布扶壁柱两侧;设备闸门部位钢衬里进行加厚处理;且在内外层间多设置相应支撑。
