关于广义i阶宽度积分的逆Brunn-Minkowski型不等式

杨 林 谭 杨 罗 淼

(1.铜仁职业技术学院 信息工程学院，贵州 铜仁 554300；2.贵州师范大学 数学科学学院，贵州 贵阳 550025)

1 引言与预备知识

文献[2]将文献[1]所研究的宽度积分推广到广义i阶宽度积分，其定义为

文献[4]研究了星体(即径向函数为连续的正的星集)的广义i阶弦长积分，若K为星体，其弦长积分可表示为

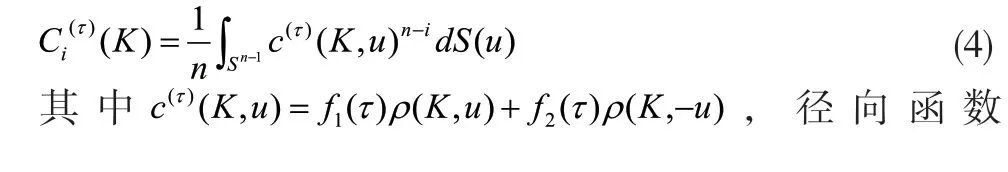
该文受文献[5]的启发，利用逆Hölder不等式推导出不等式(2)—(3)的逆不等式，即

该文与文献[6]不同的是系数与凸体无关，更多的Brunn-Minkowski不等式可参见文献[7]。

2 主要结论的证明

为得到该文结论，还需要以下引理。

整理即可得证定理1。

应用不等式(7)与引理3给出如下关于宽度积分形式的逆的Beckenbach-Dresher’s不等式[10]。

定理2的证明 由于

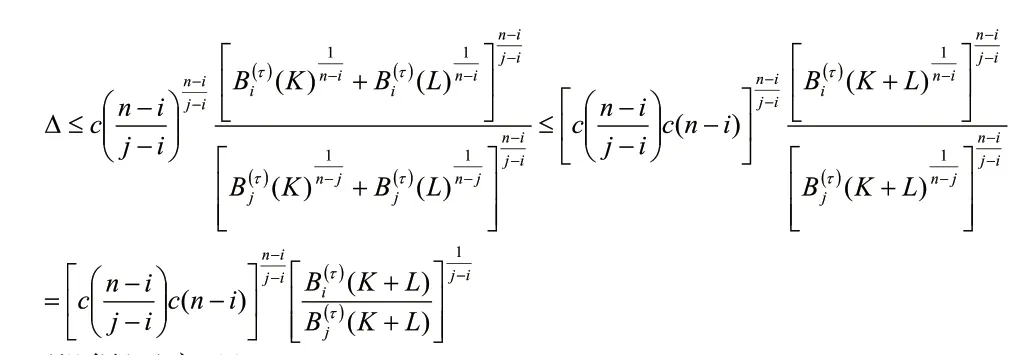
即得证定理2。

运用定理1与定理2的思想与方法可得到弦长积分的类似结论，即：