环城互通立交出入口车道数合理配置研究
2022-10-16郁伟
郁伟
(杭州市交通规划设计研究院有限公司,浙江 杭州 310030)
0 引言
环城互通立交是都市交通的“大动脉”,是满足现代化城市交通流量设计、决定城市交通发展的关键,环城互通立交作为城市交通系统的重要节点,对城市环岛出入口和行车方向转换具有重要作用。环城立交出入口位置是城区快速交通的瓶颈,大部分城区快速交通的拥堵发生地集中在环城立交附近,出入口车道数如果合理配置可以提高整体的运输效率。针对环城立交路口及匝道的优化设计在城区交通规划设计中占重要地位。日常交通调度中发现,高架路出入口位置如果出现设计规划问题,不但会造成局部交通拥堵,还可能增加事故率,车辆强行变道及紧急制动等可能导致突发的连续追尾事故,导致交通系统长时间拥堵。
黎俊廷[1]等通过对波士顿中央干道改造的分析研究,对城市高架路产生的负面影响和高架路改造方式进行了分析,对高架路改造的困难和收益进行了研究,并提出相关建议。魏贺[2]等对首尔市核心地区的一条高架路改造的空中步行街进行研究,从中得到经验和启示。张子寒[3]等通过识别拥堵特征、选用线性回归等方法对上海市高架路非高峰时段拥堵状况和成因进行了研究,以求找到缓解上海市高架路非高峰时段拥堵的原因,并提出相关建议。贾浩波[4]对长风港区铁路专用线综合选线进行分析,分析选项的控制因素和设计思路,为同类铁路专用线的设计提供借鉴。徐炜[5]结合实际案例,对工程实践中常见的限制进行分析,对城市近距离错位交叉口改造设计方法进行探讨,为提出交通管理或工程改造措施提供参考。袁湘华[6]等针对兴义环城高速公路项目中出现的互通重叠问题,并为了满足地方道路上下高速的需求,从优化路网节点出发提出3种方案,择优对兴义互通进行改造。周月明[7]通过对广州周边高速公路的堵塞问题进行分析,制定了分时限货“限导结合”的方法,为研究者进行科学的交通疏导提供了理论。薛艳婷[8]通过对重丘区互通式立体交叉互通方案的分析,对山区互通式立体交叉的特点进行分析,总结了山区互通式立体交叉的设计要点和技术要求,为设计者提供了更多的指导,确保了设计方案的合理性,有效地控制工程规模。
早期研究对周期性数据一般优先选用超限学习机算法,而对不完备数据的挖掘任务一般选用神经网络。而元胞自动机算法为形成体系之间,蚁群博弈算法属于管用方法,即相关研究一般使用神经网络、超限学习机、元胞自动机、蚁群博弈等算法进行相关设计。这些算法各有优劣,本文研究基于元胞自动机设计一种环城立交仿真算法,与其他文献中使用的算法模型进行比较,开发一种具有一般性的环城立交路口设计仿真方案。
1 环城立交出入口的一般模式
环城立交入口一般包含多条直行车道,而出口包含1条或多条匝道出口,用于驶入或驶出环城快速路的车辆,另包含1条或多条直行出口,用于保持在环城快速路的车辆,车辆行驶到某概率塌缩点后,其进入匝道或进入直行的叠加态概率发生塌缩成为确定值,在进入塌缩点之前,车辆一定概率发生变道、变速操作。该环城立交出入口的逻辑架构如图1所示。
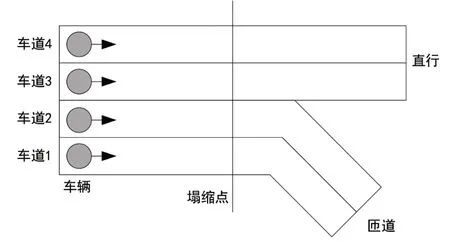
图1 环城立交出入口的概率逻辑图
图1描述了一种特殊模式,入口包含了四条直行车道,出口包含了两条匝道车道和两条直行车道,车道起始点按一定概率驶入车辆,车辆在抵达塌缩点前,使用2个线性概率函数控制其车速变化和车道改变。该元胞自动机重点控制从车辆进入点到塌缩点之间的仿真数据。即该模型中以车辆为元胞单元,以车辆进入点到塌缩点的车道空间为元胞空间,具体模型设计在下文中进行分析。
2 元胞自动机模型设计
该元胞自动机模型以车辆为元胞单元,通过随机数发生器分别投入车道中,赋予其速度属性、加速度属性、变道概率属性,每时间单元判断一次状态,车辆投入点到塌缩点距离设定为120m,其各属性关系如下:
(1)每时间节点在车道的车辆投入点作出一次判断,判断函数为:

式(1)中:Rand()为随机数发生器,产生[0,1]区间上的随机双精度数值;ζB为车辆发生的调整系数;Bin()为二值化函数,将结果调整到[0,1]区间的两端,当最终输出结果为1.000时,则该车道投入一辆车,当最终输出结果为0.000时,则该车道不投入车辆;通过调整ζB对元胞自动机的车辆投入过程进行整理。
(2)车辆投入后,每个车辆作为一个元胞进行控制,当符合以下公式时,进行车道变换:
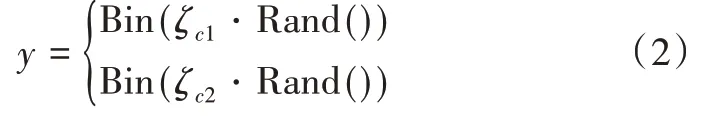
式(2)中:ζC1和ζC2为向左变换车道和向右变换车道的调整系数;其他数学符号含义同前文公式(1),当上述两个公式输出值均为1或均为0时,车辆元胞单元不发生车道变换,当上述两个公式输出值有且只有一个为1时,发生对应车道变换,当车辆位于最左侧车道或最右侧车道且触发超出车道边界的变换时,丢弃该车道变换结果不予执行。
(3)控制车辆元胞单元车道变换的同时,使用式(3)判断其车速:

式(3)中:v0为上一个时间周期判断结束后的车速;v为该周期判断结束后的车速;ζV为车速变换控制系数;其他数学符号含义同式(1)、式(2)。
运行该元胞自动机时,统计每辆车在每个时间点运行的距离、位置,且设定在匝道入口处(塌缩点)车辆需要将速度调整至40km/h,车辆执行通过车速需要控制在90~120km/h,每个时间节点判断车辆间距,当两车间距为0m时,认为发生车辆碰撞,同时统计计算每时间节点通过塌缩点的车辆数量及平均车速。
3 车辆匝道数量规划设计方法仿真实证
如前文所述,当前用于车道匝道数量的论证方法包括神经网络、超限学习机、元胞自动机、蚁群博弈等,在PTV-VISSIM(微观交通仿真模型)中构建仿真环境,加载随机数发生器及路径控制控件,数据分析系统采用相关文献中使用较广的空间卷积神经网络与模糊卷积神经网络综合的机器学习系统,受制于篇幅,此处不展开讨论具体算法。参考相关文献对上述4种方法分别构建仿真环境,以某道路所有路口的实际天眼系统实测数据为原始数据,实现车道匝道数量的计算结果。
首先,分别以神经网络、超限学习机、元胞自动机、蚁群博弈算法得出的数据作为A变量,实测数据为B变量,对其执行SPSS下的双变量t校验和非线性曲线估计验算,R2值的统计方法为回归残差与均值残差的比值,如公式(4):

式(4)中:为考察样本序列算术平均值;x͂i为序列中第i个回归值;xi为序列中第i个输入值;n为考察样本数量;双变量t校验的t值与P值来自双变量t校验过程。其中,t值为输出结果的Value值,当t>10.000时,认为两列数据存在统计学一致性,且t值越大,一致性越大;P值为输出结果的Log值,当P<0.05时,认为结果数据在置信空间内,当P<0.01时,认为结果数据具有显著的统计学意义,P值越小,可置信程度越高。受制于篇幅,此处仅解释t值(Value值)的计算算法,如公式(5):

式(5)中:为考察样本序列算术平均值;μ为参照样本序列的平均值;n为考察样本序列的节点数;m为参照样本序列的节点数;σx为考察样本序列的标准偏差率。双变量t校验结果与非线性曲线估计结果的数据质量比较见表1。

表1 双变量t校验结果与非线性曲线估计结果的数据质量比较
表1中,t值与P值来自双变量t校验结果的Value值和Log值,当t<10.000时认为两组数据存在数据差异,且t值越小,数据差异性越大,表中所有t值均有t>10.000,即所有仿真数据均与实测数据之间没有统计学差异,但元胞自动机的t值最大,证实其与实测数据之间的一致性更强。当P<0.05时认为比较结果处于统计学信度空间内,当P<0.01时认为比较结果具有显著的统计学意义,4组数据中,只有元胞自动机数据存在P<0.01,其他三组数据均处于0.01<P<0.05区间,得知元胞自动机的数据信度最高。R2值来自非线性曲线估计中的残差比较值,及数据残值与数据差值之间的比值。R2值越大,证实曲线估计结果与原始结果的数据耦合性更高,其中元胞自动机算法的R2值最大。
其次,以该路实测车流量为基础数据,比较相同车辆流量目标下4种算法给出的匝道车道数、直行车道数和总车道数,如表2所示。

表2 四种算法的车道规划结果比较
表2中,统计每个路口的设计车道数量,计算其算术平均数,以小数点后1位计算,谷值冗余度是当车流量达到谷值时(如凌晨),车道的空余量,以百分比计算。最终发现相同设计目标下,元胞自动机给出的规划车道数最少,谷值冗余度最小,证实元胞自动机算法的规划最为保守,涉及的改造投资最小。以该个案中涉及的某道路为例,目前为双向6车道,即单向3车道不含潮汐车道,元胞自动机涉及结果中单向3.8车道均值结果最接近当前的车道数量。
4 结语
该研究设计了一种用于城市高架路路口规划设计的元胞自动机算法,以某道路所有路口的实际天眼系统实测数据为原始数据,实现车道匝道数量的计算结果;参照相关文献构建了仿真比较使用的神经网络算法、超限学习机算法、蚁群博弈算法;以各算法得出的数据作为A变量,实测数据为B变量,对其执行SPSS下的双变量t校验和非线性曲线估计验算,表中所有t值均有t>10.000,即所有仿真数据均与实测数据之间没有统计学差异,但元胞自动机的t值最大,证实其与实测数据之间的一致性更强。4组数据中,只有元胞自动机数据存在P<0.01,其他三组数据均处于0.01<P<0.05区间,得知元胞自动机的数据信度最高R2值越大,证实曲线估计结果与原始结果的数据耦合性更高。其中,元胞自动机算法的R2值最大。然后以实测车流量为基础数据,比较相同车辆流量目标下4种算法给出的匝道车道数、直行车道数和总车道数,在相同设计目标下,元胞自动机给出的规划车道数最少,谷值冗余度最小,证实元胞自动机算法的规划最为保守,涉及的改造投资最小。
该研究发现元胞自动机算法的仿真结果与实测结果吻合度最高,且规划结果对当前方案的改动最小,所以,推荐在城市高架路规划设计中优先使用元胞自动机算法。该研究的仿真实验中虽然选择个案为例,但同样可以用于目前的城市高架桥出入口车道设计。后续研究中将进一步拓展一般性研究,进一步优化元胞自动机算法在城市高架路路口设计中的普适性。
