北极冰川槽谷发育的形态特征分析

王泽民 张曲辰 金爽 艾松涛

（武汉大学中国南极测绘研究中心，湖北 武汉 430079）

0 引言

冰川槽谷是由冰川侵蚀作用过的谷地, 这种地貌的主要成因是冰川侵蚀作用, 冰川槽谷的侵蚀作用主要分为冰川下蚀和侧蚀拓宽, 冰川侵蚀作用的不同也会影响冰川槽谷形态发育的差异,由冰川槽谷的横剖面轮廓判别槽谷形态发育的程度, 进而判断冰川侵蚀的作用模式是一种研究的新思路。根据槽谷外部轮廓的形状差异, 冰川槽谷分为V型谷和U型谷[1], 从V型谷到U型谷的演化过程称为冰川槽谷的完整发育过程[2]。

1959年Svensson[3]建立了幂函数模型, 该模型可以使用幂函数方程对冰川槽谷的外部形态进行数值模拟进而得到冰川槽谷的定量化描述。相较于其他模型, 幂函数模型在比较不同槽谷横剖面及研究槽谷形态发展中更具优势[2,4]。但是这个模型存在系统性的缺陷, 幂函数模型参数相同的槽谷剖面, 形态上可能存在的巨大差异,Graf[5]引入的槽谷宽深比(FR)限定了槽谷的宽度与深度比例, 完善了最初的模型。1984年Wheeler[6]对位于阿伦岛的Glen Rosa冰川槽谷的两段分别进行了拟合, 得出了用幂函数描述冰川槽谷横剖面时, 槽谷的不同坡段幂函数模型参数存在差异的结论。

在冰川槽谷定量研究的发展历程中, 幂函数模型法自提出以来已被国内外学者广泛应用、研究。此方法的优势在于简化了方程的计算, 除此之外还有悬链线模型法及二次多项式方法也可用于冰川槽谷发育的定量研究中。三种常见的方法均可应用于大多数具备V型至U型演化特点的冰川槽谷, 但因悬链线模型法方程式复杂不便计算,二次多项式方法无法适用于对称性差的冰川槽谷的原因, 幂函数模型法成为冰川槽谷形态研究的主流方法。国内学者[7-8]对幂函数模型法已有广泛应用, 该方法成功应用于天山乌鲁木齐河源1号冰川及白马雪山冰川的研究。

国内外学者[9-12]对Austre Lovénbreen冰川和Pedersenbreen冰川的研究主要集中于冰川物质平衡、冰川地形测量、冰川表面积雪覆盖率及冰流速研究中, 因 Austre Lovénbreen 冰川和Pedersenbreen冰川的底部温冰层含水量较大难以直接观测冰下地形[13], 冰面之下的冰川槽谷发育的形态特征缺乏定量性的分析研究。本次北极山地冰川的数值模拟实验对冰川槽谷的形态发育进行了基于幂函数模型的定量分析, 计算了冰川槽谷各个横剖面与幂函数模型拟合的各项参数, 对比分析了两个冰川槽谷发育过程存在的差异并探究了差异的成因。

1 研究区域简介

北极斯瓦尔巴地区是目前国际冰川研究的热点地区, 该群岛总面积约59250 km2, 其中超过57%的面积被2100多个冰川覆盖。该区域的大多数冰川都是多温冰川, 而本文选取的研究对象Austre Lovénbreen冰川和Pedersenbreen冰川是两个典型的多温山谷冰川[13](图1)。

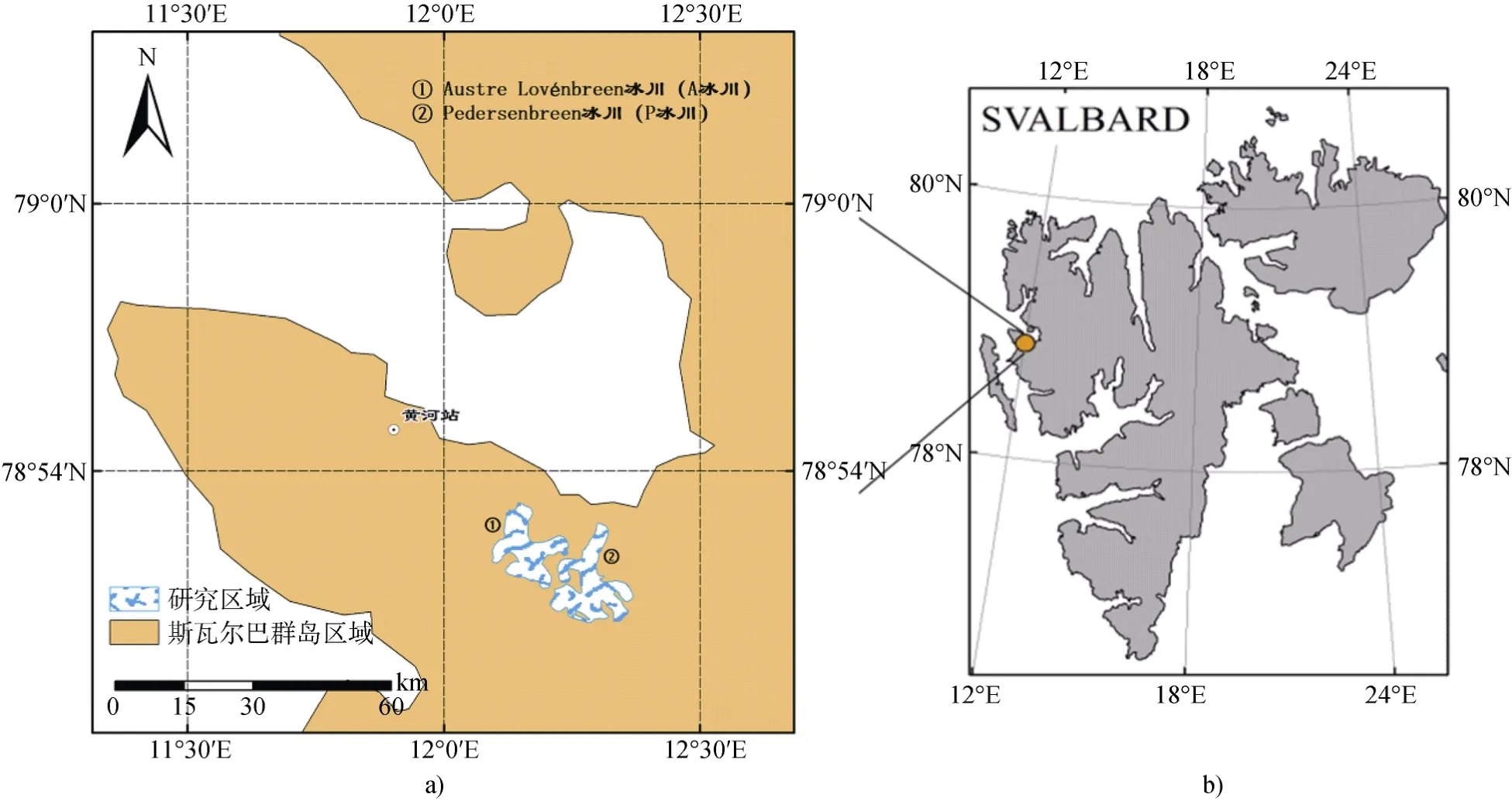
图1 研究区域。a)北极黄河站、A冰川、P冰川位置示意图; b)斯瓦尔巴群岛示意图及研究区域所处的位置Fig.1.The study area.a) location map of the Yellow River Station, Austre Lovénbreen and Pedersenbreen; b) location of study region in Svalbard

2004年, 我国首次北极黄河站科学考察后, 将Austre Lovénbreen冰川(下文中简称为A冰川)、Pedersenbreen冰川(下文中简称为P冰川)列为长期监测冰川。2005年, 科考队员在两条冰川上埋设标杆,其中A冰川表面埋设17根, P冰川表面埋设5根, 用于监测冰川物质平衡的变化及高精度GPS测量[14]。2009年, 我国科考队员利用单频GPS接收机和探冰雷达(Ground Penetrating Radar, GPR)在两条冰川表面采集了密集的GPS及GPR数据, 开展了冰面地形和冰下地形的研究[15-16]。

2 数据采集及处理

2.1 数据来源

本次实验所用数据是我国北极科考队员采集于2009年4月的GPS数据及GPR数据。在数据采集的过程中, 将考察设备固定在自制的木质雪橇上, 前雪橇组安装GPR主机、接收天线和GPS接收机(图2), 后雪橇组安装GPR发射天线, 用雪地摩托车牵引自制的雪橇在冰面上同步采集GPS数据和GPR数据[15,17]。其中GPS数据是由加拿大NovAtel公司生产的SMATY-V1型一体化GPS接收机采集, GPR数据则由加拿大Sensor&Software公司生产的pulseEKKO PRO型探地雷达采集。与此同时使用双频GPS对测桩进行多次测量, 获得精度优于1 cm的冰面流速[12,18]。

图2 雪地摩托牵引雪橇组工作现场: 木质雪橇搭载的GPR和GPS测量系统Fig.2.Field work by snowmobile and sleds: GPR & GPS surveying instruments were loaded in wooden sleds

在采集过程中, 获得A冰川表面23500个测点的数据, 测线里程达到了83.2 km; P冰川表面采集了17200个测点的数据[16], 测线里程达到了47.4 km, 具体采集区域及测线分布见图3。

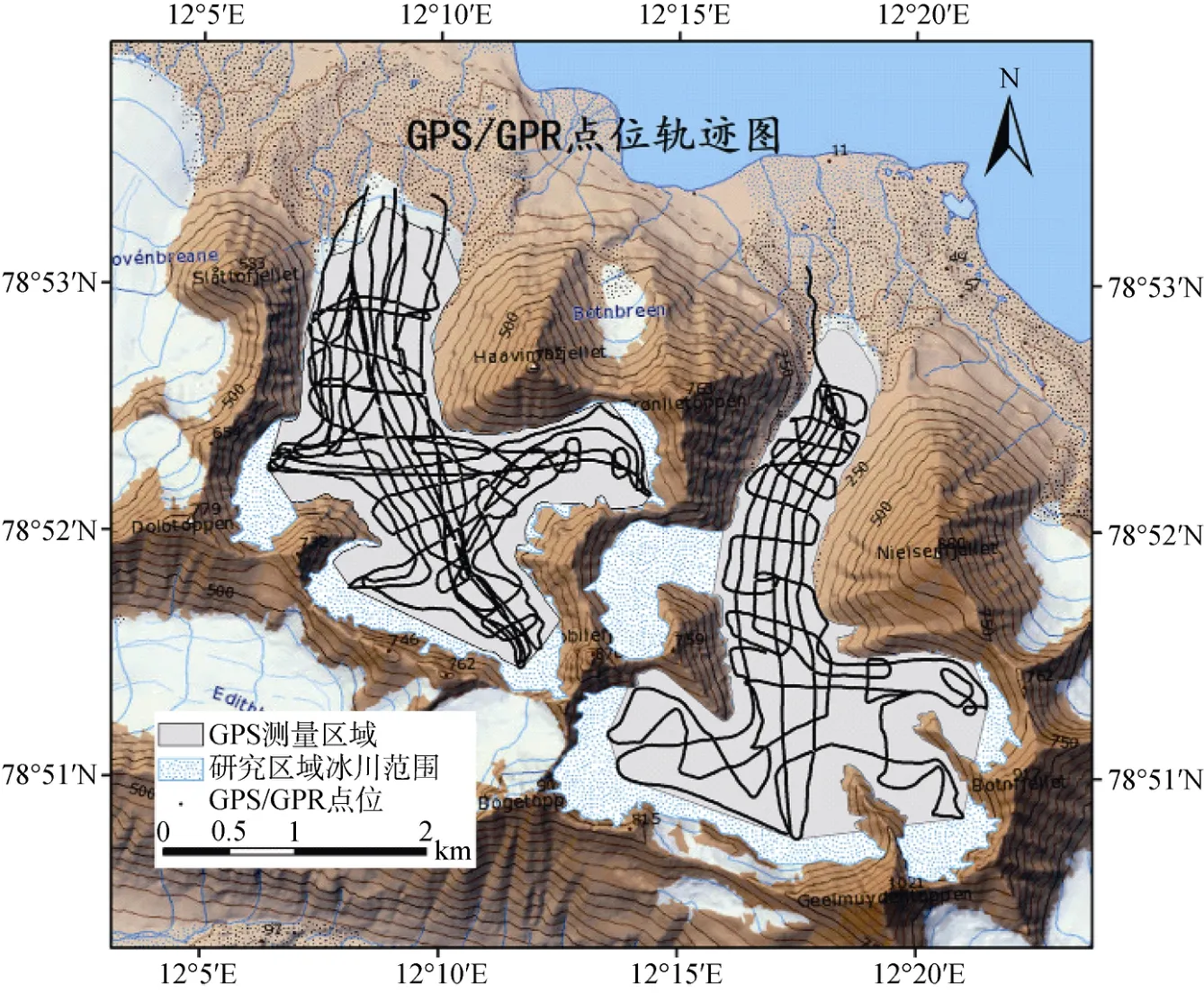
图3 北极A冰川、P冰川处GPS/GPR测线分布图[19]Fig.3.Acquired GPS/GPR points in surveying lines in Austre Lovénbreen and Pedersenbreen, Arctic[19]

2.2 数据处理

在上述实验所用的GPS数据及GPR数据采集完毕后, 利用TGO软件和EKKO Deluxe软件分别对GPS数据和GPR数据进行预处理, 之后利用自主开发的GPRead软件, 实现GPS数据读取、平差处理、残差平滑和精度评定, 以及对GPR数据的深度提取[15,17]。经残差平滑后, A冰川表面的GPS测线交叉点高程最大互差为1.43 m, P冰川表面的GPS测线交叉点高程最大互差为-0.71 m,GPS交叉点高程平均误差达到分米级。对实时动态测量数据(RTK)的自然邻近插值获取了冰川表面数字高程模型(DEM)。

使用探底雷达对冰层厚度进行测量, 本次数据采集所使用的探地雷达分为两种频率类型, 在冰厚小于100 m的绝大多数区域使用频率为100 MHz的雷达采集冰厚数据; 在冰厚大于100 m的局部地区使用频率为5 MHz的低频雷达,避免了冰层底部处于压融状态的温冰无法被高频信号穿透的问题[13,17]。冰面DEM与探地雷达测量得到的冰厚相减得到冰川底部DEM, 冰川表面、底部的DEM空间分辨率均为10 m[15,17], 数据处理结果如图4所示。

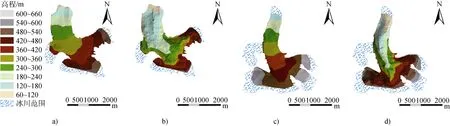
图4 经GPS、GPR数据处理的冰川表面、底部地形DEM。a) A冰川表面DEM; b) A冰川冰下DEM; c) P冰川表面DEM; d) P冰川冰下DEMFig.4.Surface DEM and bedrock DEM of glaciers.a) surface DEM of Austre Lovénbreen; b) bedrock DEM of Austre Lovénbreen; c) surface DEM of Pedersenbreen; d) bedrock DEM of Pedersenbreen

3 研究方法

3.1 幂函数模型的应用

冰川槽谷在地貌学的分类中以抛物线形态为主, 本文利用计算抛物线的研究方法[3], 构建冰川槽谷形态的幂函数模型, 假设冰川槽谷的横截面近似为y=axb, 其中x,y分别为原点到槽谷横剖面上点的水平距离和垂直距离, 通过确定系数a及指数b可以判断冰川槽谷的形态和发育情况。

为了方便计算, 对幂函数模型两边取对数,将函数y=axb转化为Y=A+bX, 其中Y=lny,A=lna,X=lnx。之后采用最小二乘法确定线性关系中的常数A与b, 在残差平方和出现最小值时常数A、b为数值模拟的最优解:

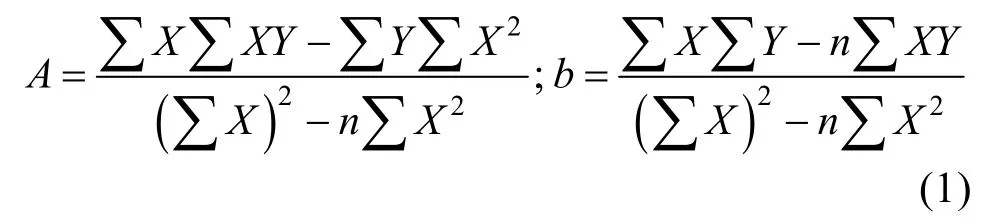
式中,n为观测值样本数。

在冰川槽谷的发育过程中, 冰川规模和侵蚀能力决定了槽谷的形态[20-21]。因冰川侵蚀作用在不同位置的差异较大, 仅用一组幂函数模型参数A、b来描述冰川槽谷的横剖面是不准确的, 所以需要在不同海拔位置提取多个横剖面, 利用幂函数模型开展分析。幂函数模型需要以各横剖面最低点为原点, 在原点两侧分别进行拟合, 以获取对应坡段的幂函数模型参数[6]。

在y=axb中,a值描述谷底的宽阔程度,b值反映槽谷的发育情况及陡峭程度[21]。在数值范围上b值具有很大的变化范围, 通常范围为1≤b≤5, 当b值靠近1时, 冰川槽谷接近于V型谷;b值大于2时, 冰川槽谷更接近于U型谷, 一个冰川槽谷的完整发育过程就是V型谷向U型谷的演化过程[2]。

3.2 槽谷宽深比对幂函数模型的补充

幂函数模型y=axb作为冰川槽谷定量描述的数学模型具有片面性, 这是由幂函数曲线的性质所决定的, 针对同一幂函数模型, 可完成对形态不同(主要指宽度、深度不同)的冰川槽谷曲线的拟合。因此, 为了更加精确地用数值模型表示冰川槽谷的形态, 需引入其他参数描述冰川槽谷横截面的几何形状, 以避免两段不同的冰川槽谷回归曲线相同。

槽谷宽深比保证了基于幂函数模型的冰川槽谷的唯一性, 其本质是使用正比例函数对符合幂函数模型的冰川槽谷形态进行约束, 只有槽谷宽深比与幂函数一起使用才能描述和限定冰川槽谷的形态。槽谷宽深比的引入克服了幂函数模型的局限性, 更加准确地表示了冰川槽谷的横截面几何形状, 并忽视量纲的影响, 精确了先前的幂函数模型[5]。槽谷宽深比(FR)被定义为槽谷深度(D)和谷顶宽度(WT)之比:

FR保证了基于幂函数模型的冰川槽谷的唯一性, 其本质是使用正比例函数对符合幂函数模型的冰川槽谷形态进行约束, 只有FR与幂函数一起使用才能描述和限定冰川槽谷的形态。

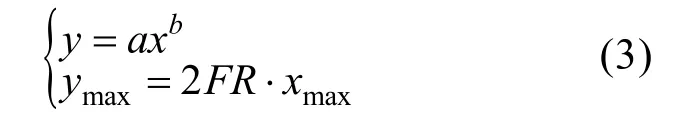
式中,ymax为冰川槽谷的槽谷深度D,xmax为谷顶宽度WT的一半。

式中正比例函数用于约束冰川槽谷的形态,FR的几何意义是正比例函数斜率的一半, 图5为FR对槽谷形态限制示意图。

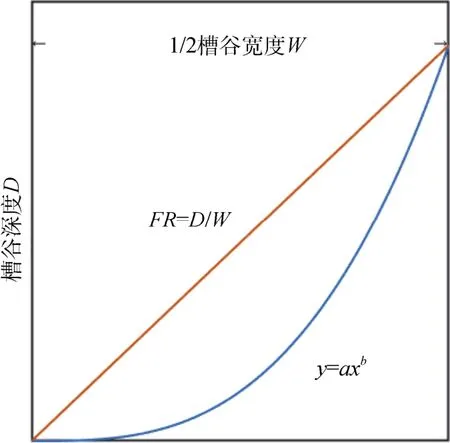
图5 槽谷宽深比对冰川槽谷形态的限制[5]。红线为受宽深比影响的正比例函数曲线;蓝线为与幂函数模型曲线拟合的冰川槽谷Fig.5.The constraint of Form Ratio (FR) to morphology of glacial valley[5].The red line is constraint function curve affected by FR; the blue line is curve of glacial valley which fitted to the power law model

4 结果与讨论

4.1 b值分布及其反映的冰川槽谷发育情况

使用2009年科考队员所采集的A冰川、P冰川的GPS数据和GPR数据, 分别制作显示冰川槽谷发育形态的剖面图[15,17]。在A冰川主流线上选取9个横剖面, 另外在东部支流截取4个横剖面, 横剖面截取见图6a所示; P冰川则只在主流线截取10个横剖面, 横剖面截取见图7a所示。在剖面的截取过程中沿主流线做大量剖面, 根据剖面形态特征手动提取符合幂函数曲线的剖面,再由幂函数坐标原点附近的沉积情况为判据, 将剖面中冰下地形曲线受沉积物影响严重的对象剔除, 避免沉积物覆盖的影响, 因此在参数的拟合过程中保证了数据的精确性。

截取所得的A冰川、P冰川的各横剖面数据折线图分别见图6b、图7b, 之后将处理过的GPS数据和GPR数据与取对数的幂函数模型Y=A+bX拟合, 经求解后获得各横剖面的b值, 如表1～3所示, A冰川的b平均值范围为0.7554～1.7289, P冰川的b平均值范围为1.0250～1.8738, 由于两冰川槽谷b值范围均小于2, 可得出两者更接近于V型谷而非U型谷。通过分析b值的分布情况, 发现在两条冰川中部雪线附近, 即冰流速最快的区域均出现b值的极大值; 另外, 通过高精度GPS点监测获取P冰川及A冰川主流线上的流速, 发现P冰川整体冰流速是A冰川整体冰流速的2倍以上[12,18], 且P冰川相较于A冰川在下游b值更大, 证明P冰川槽谷发育情况优于A冰川, 即冰川槽谷发育程度与冰流速之间存在着正相关的关系。此外, 在同一条冰川内部, 随着冰流速增大,b值也增大, 表明在冰流速越大的位置发育成型为U型谷的可能性越高。A冰川、P冰川沿主流线上各位置流速数据如图8所示, 该流速数据分别为2009—2015年A冰川、P冰川的平均速度, 图8a中各标号是A冰川沿主流线自下游至上游布设的6根监测标杆的编号, 图8b中P1—P5是P冰川沿主流线自下游至上游布设的5根监测标杆的编号, 监测标杆具体位置可参考图6a、图7a主流线上黑点位置。

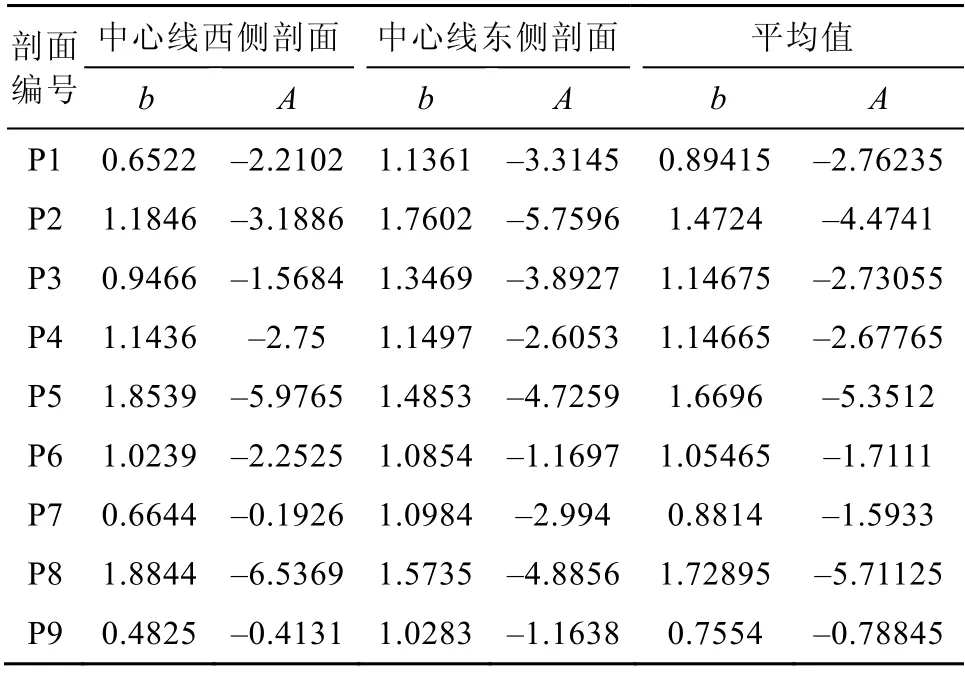
表1 A冰川干流横剖面幂函数模型参数Table 1.Parameters of power law model in central line of Austre Lovénbreen

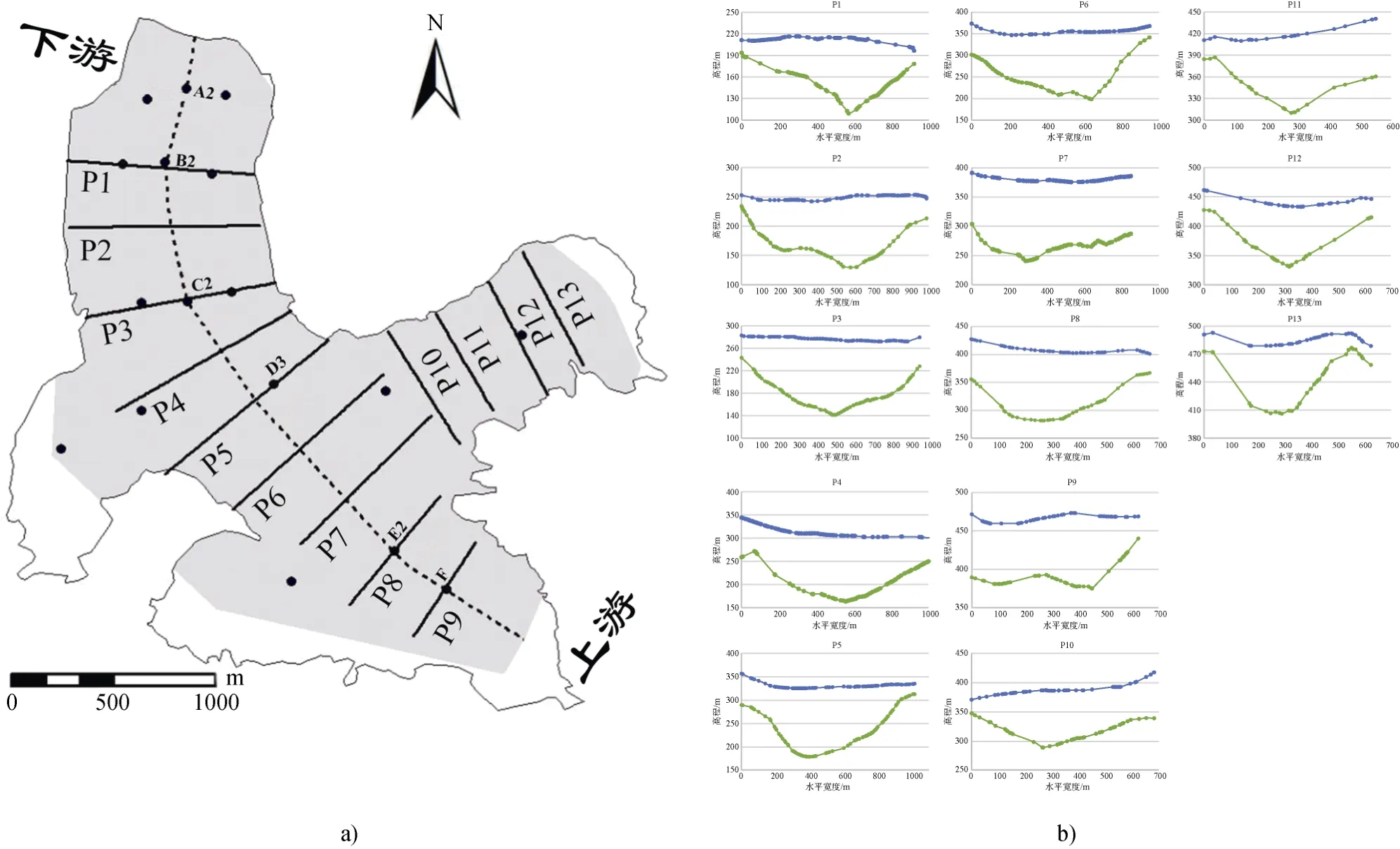
图6 A冰川槽谷剖面图。a)A冰川的槽谷横剖面位置示意图, 黑点为冰流速监测的观测标杆布设位置; b)A冰川的横剖面图, 其中蓝色为冰面曲线, 绿色为槽谷形状Fig.6.Cross-sections in Austre Lovénbreen.a) the location map of cross-section in Austre Lovénbreen, the black sign is the location of monitoring stakes; b) profiles in Austre Lovénbreen, the blue line shows ice surface and the green line shows the shape of glacial valley

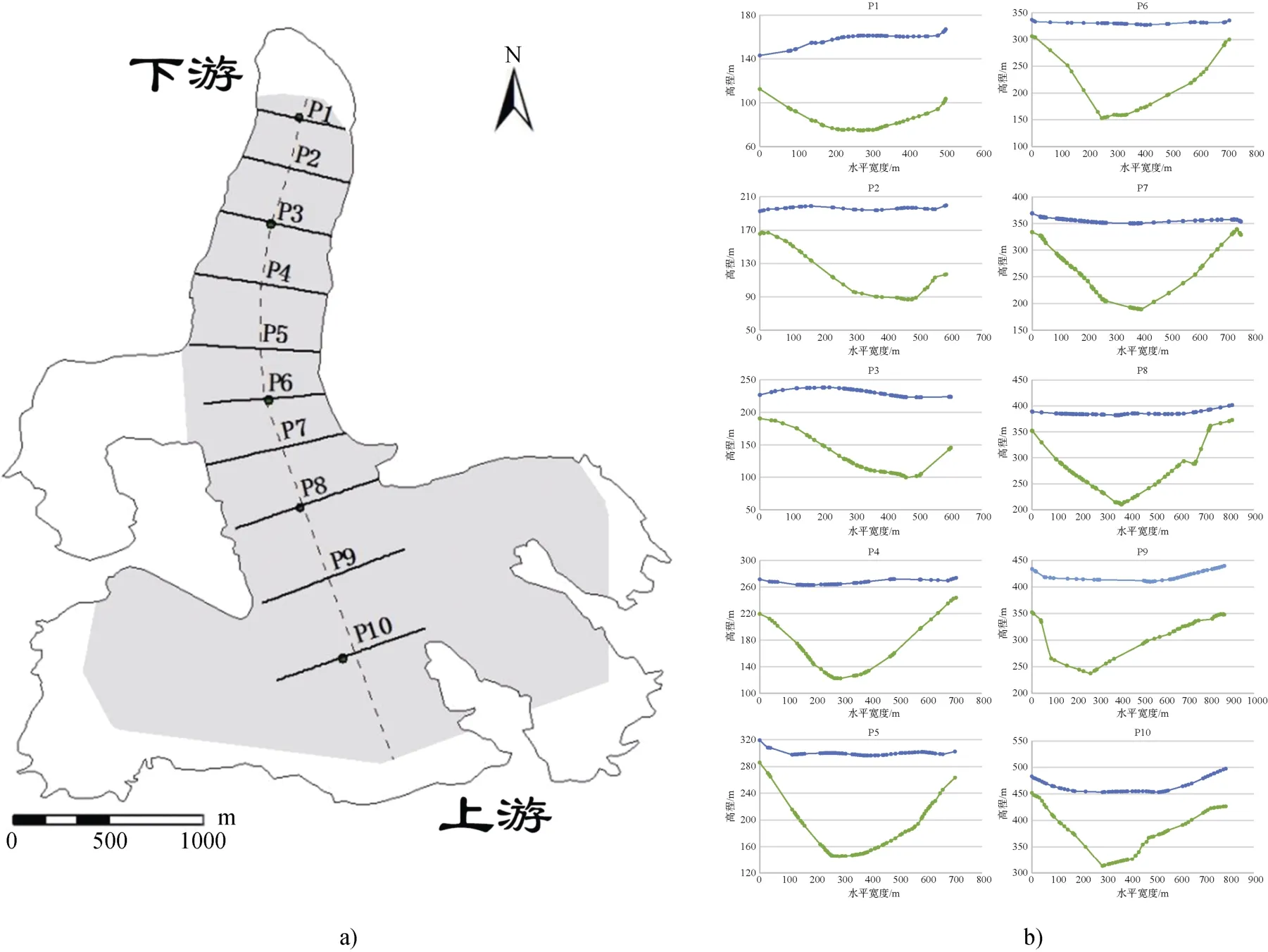
图7 P冰川槽谷剖面图。a) P冰川的槽谷横剖面位置示意图; b) P冰川的横剖面图, 其中蓝色为冰面曲线, 绿色为槽谷形状Fig.7.Cross-sections in Pedersenbreen.a) the location map of cross-section in Pedersenbreen; b) profiles in Pedersenbreen,the blue line shows ice surface and the green line shows the shape of glacial valley

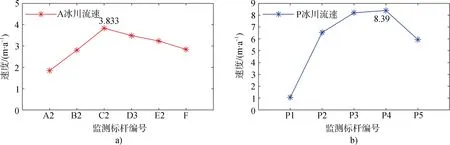
图8 A冰川与P冰川流速对比。a)A冰川主流线速度分布; b)P冰川主流线速度分布Fig.8.The comparison of ice flow velocities between Austre Lovénbreen and Pedersenbreen.a) the velocities alone the central flow line in Austre Lovénbreen; b) the velocities alone the central flow line in Pedersenbreen

4.2 b-FR关系分析

FR是冰川槽谷发育形态研究中的一个重要影响因素, 可以通过FR与幂函数指数b的相关性判断该冰川槽谷发育过程中所受冰川侵蚀的具体作用形式[22-25]。当FR值与b值呈正相关关系时,表明冰川槽谷的形成过程中下蚀作用为冰川侵蚀的主要形式;FR值与b值呈负相关关系时, 表明冰川槽谷的形成过程中侧蚀作用为冰川侵蚀的主要形式。

使用A冰川、P冰川各横剖面b值和FR值作散点图, 由图9a可知A冰川b-FR关系总体呈正相关, 冰川槽谷受冰川侵蚀作用主要以下蚀作用为主, 表现为典型的山地冰川模式; 由图9b可知P冰川中b-FR关系总体呈现一定的负相关关系, 侧蚀作用强于下蚀作用; P冰川下游的槽谷发育优于A冰川, 形态更接近于U型谷。

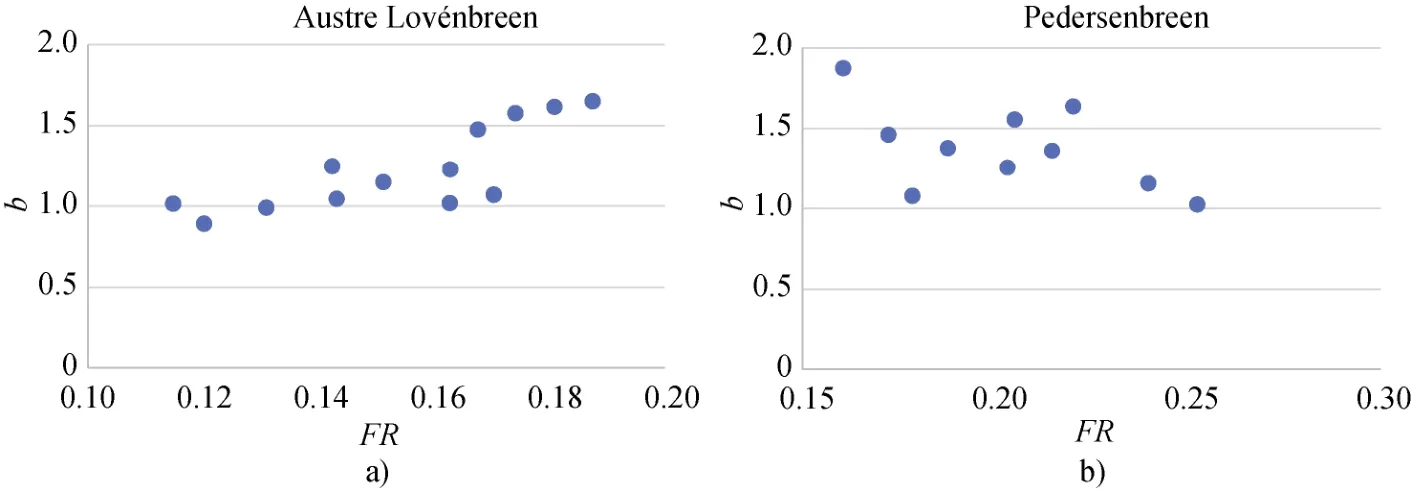
图9 各横剖面b-FR关系。a)A冰川各横剖面b-FR关系散点图; b)P冰川各横剖面b-FR关系散点图Fig.9.Relation between b and FR.a) relation between b and FR of Austre Lovénbreen; b) relation between b and FR of Pedersenbreen

4.3 |A|与b关系分析

在用幂函数模型表示冰川槽谷的过程中, 参数a、b是描述冰川槽谷发育形态的重要参数, 故a、b的关系对冰川槽谷形态特征具有一定的研究意义[21]。由于a值数值过小, 甚至会小于b值数个数量级,a、b之间线性关系不显, 故研究a值的对数值A与b值的关系。

通常情况冰川槽谷的幂函数模型中幂函数系数a值范围为0＜a＜1, 可得出a的对数化的结果A为负数, 取两冰川各横剖面所得数据|A|、b分别作各自的回归曲线, 如图10所示。

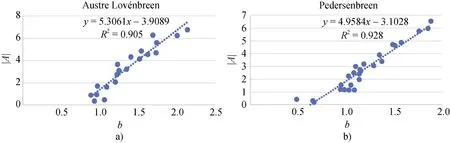
图10 |A|与b关系。a) A冰川; b)P冰川Fig.10.Relation between |A| and b.a) Austre Lovénbreen; b) Pedersenbreen

A冰川各横剖面|A|与b拟合的回归方程为y=5.3061x-3.9089, 相关系数r=0.951, P冰川各横剖面|A|与b拟合的回归方程为y=4.9584x- 3.1028,相关系数r=0.963。根据所得数据可知两条冰川的|A|与b表现出了很强的线性相关,|A|随b值增大而增大, 两条冰川的趋势相一致; 比较分析两条冰川的曲线斜率, 发现两者曲线斜率相近, 表明两条冰川槽谷形态特征为同一类型, 均为V型谷; A冰川的拟合曲线可以近似看做是P冰川拟合曲线向上平移的结果, 如果取相同b值的情况下, A冰川的|A|值将大于P冰川, 则A冰川的a值更小, 谷底相较P冰川更宽阔。

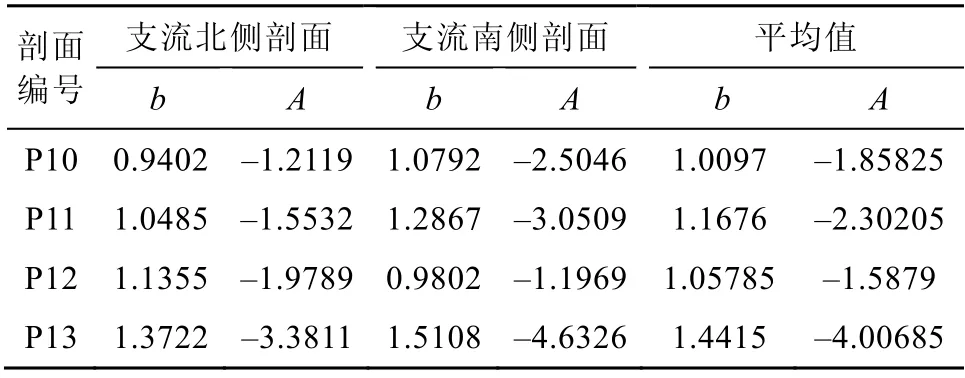
表2 A冰川东部支流横剖面幂函数模型参数Table 2.Parameters of power law model in the eastern of Austre Lovénbreen

5 结论

本文使用2009年北极科考队员所采集的Austre Lovénbreen冰川、Pedersenbreen冰川的GPS数据及GPR数据进行处理后, 采用幂函数模型, 引用槽谷宽深比等概念对两冰川的冰川槽谷的发育形态进行系列数值模拟工作, 研究分析后结论如下。

1.A冰川、P冰川各横剖面所得b值反映冰川槽谷的发育情况, 两者b值范围均小于2, 其中A冰川b值范围为0.7554～1.72895, P冰川b值范围为1.0250～1.8738, 地貌形态都表现为V型谷, P冰川槽谷相较A冰川槽谷更加接近于U型谷。同一条冰川内,b值与相应位置的冰流速呈正相关关系。

2.引入槽谷宽深比FR后发现, A冰川槽谷剖面b-FR关系总体呈正相关, 由此判断A冰川槽谷为下蚀作用为主的山地冰川模式。P冰川槽谷剖面的b-FR关系呈现一定的负相关, 由此判断P冰川侧蚀作用强于下蚀作用。

3.取对数后的幂函数模型系数|A|与b呈线性相关关系, 且两冰川槽谷|A|-b回归方程的曲线斜率数值差异不大, 再次证明两条冰川槽谷同为V型谷。从回归曲线截距判断, A冰川槽谷|A|-b回归曲线截距更大, 表明A冰川谷底更加宽阔。

致谢感谢中国北极黄河站考察队员在本研究野外调查工作中的帮助和支持。