基于EHO-FF算法的智能电网无功优化研究

李旭炯，杨郭明，孙林花

(1.兰州资源环境职业技术大学，甘肃 兰州 730021； 2.国网兰州供电公司，甘肃 兰州 730070)

智能电网优化电力生产、分配和消费，保持电网稳定运行，克服分布式发电的高渗透问题[1]，减少温室气体排放，提高电网效率与可靠性，是电力行业发展的新方向[2]。智能电网技术正在从供给侧控制的网络向需求侧互动的网络转变[3]。在智能电网中实施需求响应优势明显，能降低成本和排放、减少燃料依赖、提高系统可靠性等[3]。智能电网面临的最大挑战是如何降低系统损耗，改善母线电压，从而控制供电成本。需求侧管理(demand side management，DSM)使用户可结合具体需要选取不同用电方式，让用户通过选择发电方式和调整需求来获得更低价的电能[4]，对优化电力资源配置、促进能源利用效率提升等起到重要作用。随着可变分布式发电单元的持续发展，传感技术、数据处理、自动控制和通信等领域的先进技术在配电网中的应用越来越广泛[5]，可再生能源分布式发电已成为智能电网发展新方向。

无功优化可降低电力系统的功率损耗，改善系统的电压分布[6]。智能电网中的分散无功最优控制是一种先进的电力系统优化控制方法[7]，能降低系统有功损耗，改善电压分布，但用假设数据降低了结果准确性，增加了问题复杂性[8]。为此提出了各种优化方法，可分为集中式和分布式2类。文献[9]提出家庭DSM系统，随着配电系统负荷增加，家庭用电成本也随之增加。为降低家庭用电成本，提出基于人工神经网络算法的主动DSM。文献[10]提出的能源管理系统，通过引入可再生能源降低成本，使消费者参与智能电网技术中。文献[11]将人工神经网络与马尔可夫链结合用于不确定负荷需求的最优生成，并将改进人工蜂群算法用于能量管理系统。文献[12]提出一种基于多目标优化方法的高功能半分散电力匹配框架。文献[13]提出考虑能量流动和热交换的互联智能建筑的最优能源管理，通过功率交换和热交换增加了蓄热寿命，降低总运行成本。文献[14]建立由光伏发电、冷热电联合、储能系统和响应负荷组成的智能园区微电网模型，研究考虑价格需求响应的智能园区微电网机组最优调度策略。文献[15]提出一种进化模拟优化框架，用于在设备负载不确定的智能电网上实现“容灾”策略。文献[16]提出一种智能电网中用户损失最小化的解决方案。文献[17]提出一种基于电力系统微网格的能量管理优化方法。文献[18]开发一种有效保护隐私的电力用户控制协议，允许电力企业在不侵犯用户隐私的情况下控制电网供需。

总结近年研究成果，智能电网中无功优化可降低发电成本。考虑用户不确定负荷需求、分布式可再生能源和储能设备的情况下，由能源用户组成的配电网与电力企业双向实时通信，对电力系统无功优化。最优方法要使系统成本和损失最小化，同时满足负荷需求、储备需求和每个独立单元的物理和运行约束。但遇到中型或大型问题时，已有方法无法在规定时间内解决问题。

本研究提出以DSM为优化对象，引入象群优化-萤火虫进化(elephant herd optimization-firefly，EHO-FF)算法，来解决包括等式和不等式约束(供需平衡、母线电压、线路和无功功率限制等)的优化问题。IEEE30母线系统中，考虑不同场景下的无功最优解，基于最优无功控制方法，改善不同运行条件下电网的能效和电压分布。

1 智能电网无功优化建模

1.1 智能电网无功优化

图1为智能电网无功优化(reactive power optimization，RPO)的系统示意图。采用EHO-FF算法对所研究的系统在不同负载下进行无功优化，目标是已知系统和所有分布式发电(distributed generation，DG)单元母线的现有需求前提下，通过优化DG单元规模使功率损耗最小，并给出物理约束(发电机与松弛母线无功产生的局限性，电容器输出，变压器变比)和操作约束(除松弛母线外母线电压幅值的界限)下最优目标值(DG值、实际功率损耗和电压偏差)。

1.2 RPO目标函数

RPO目标函数为最小功率损耗Ploss，如式(1)所示。

(1)

式中：Vi为母线i的电压幅值；Vj为母线j的电压幅值；Gij为母线i与j之间的电导；θij为母线i与j之间的电压角；S为母线支路总数。

潮流方程如式(2)—式(4)所示。

(2)

(3)

(4)

无功功率产生的输出限制，静态无功补偿器的容量限制，电压幅值的规定范围(松弛母线除外)及变压器Tl抽头位置的限制如式(5)所示。

(5)

RPO变量分为状态变量(负载母线角度、电压幅值、发电机母线无功功率、松弛母线实际发电量)与控制变量(发电机母线电压、并联电容器/电抗器输出及变压器变比)。系统母线顺序定为松弛母线、发电机母线和负载母线(带有并联电容器/电抗器的负载母线在顺序中更靠前)。基于此顺序，状态变量X如式(6)所示。

(6)

控制变量U如式(7)所示。

(7)

由于RPO关注的是无功和电压分布优化，因此忽略了实际电力线路电流和松弛母线实际发电量等潮流分析中所包含的约束条件。已知有功功率，变压器与并联电容器/电抗器变比在实际中是离散变量，引入补偿函数可有效解决。

由于RPO输入中存在不确定因素，使其成为不确定的非线性规划问题，可表示为模糊数、随机数和区间。本研究中，由于RPO模型的自验证计算，因此选取区间来描述不确定性。与有功和无功变化相关的不确定性，比其他类型的不确定性(如输电线参数的不确定性)更需关注。但文献[19]只考虑了有功产生和负荷需求的不确定性。为便于理解，发电侧有功功率区间如式(8)所示。

(8)

负载侧有功功率区间如式(9)所示。

(9)

负载侧无功功率区间如式(10)所示。

(10)

在此基础上，由于发电侧母线有功功率和无功功率为确定值。推导带区间不确定性的平衡方程后，RPO数学模型如下。

minf(X,U)=[fL,fU]

(11)

h(X,U)=[hL,hU]

(12)

min(g)≤g(X,U)≤max(g)

(13)

式中：f(X,U)，h(X,U)，g(X,U)为区间函数；[fL,fU]为实际功率损失区间；[hL,hU]为潮流变化区间。

状态变量和控制变量X和U分别对应于RPO模型的X和U。由于发电侧电压由励磁系统确定，因此该模型中U为实值向量，并联电容器/电抗器输出和变压器变比也需调整。与X不同，U是由区间值组成，具有不受控的特点。此外，X由U通过区间潮流方程确定，即每一个U对应一个X。因此采用具有区间不确定性的非线性规划问题来解决，通过EHO-FF算法求解不确定潮流方程区间，进一步提高精度。

2 EHO-FF算法

由于EHO算法搜索性能较差，因此引入FF算法提高EHO算法的搜索性能。EHO-FF算法通过控制不同负载下的损耗，优化无功功率，其程序简单，易于实现，计算效率高。

2.1 EHO算法优化

EHO算法是一种基于群搜索最优解的启发式算法，通过象群同类相识的行动原理来寻求系统最优策略，算法内容包括氏族更新与氏族分离。一般来说，每个氏族中的母系族长都是最年长的，作为优化问题，可将氏族中的母系族长想象为最适合的象个体，大象的放牧行为被设定为氏族更新算子和分离算子。

2.1.1 更新算子

氏族更新中，大象依据母系族长为中心原则进行更新。氏族中每一头大象的下一个位置都受到母系族长的影响[20]。设每个氏族有j头大象，象群母系族长位置标记为ci，则象群更新后位置模型如式(14)所示。

(14)

需注意的是，有可能象群中存在多个母系族长，而氏族的更新变化可能只有一个中心，因此母系族长的位置受中心位置的限制，如式(15)—(16)所示。

(15)

(16)

2.1.2 分离算子

经过一段时间后，成年大象会离开原氏族重新建立新氏族[21]。利用EHO分离算子，将适应度最差的大象从氏族中分离出来。求解优化问题时，该分离过程可作为分离算子。为提高EHO算法的可搜索性，假设所有氏族中适应度最差的大象个体都采用分离算子，如式(17)所示。

(17)

2.1.3 精英策略

与其他启发式算法一样，精英策略用于关注由于部落更新和分离算子淘汰的大象个体，保证后来的大象比之前更好。首先最优大象个体被保存下来，搜索结束时，最差的大象被保存下来的最优大象替换。通过FF算法改进搜索过程，提出的EHO-FF算法流程图如图2所示，主要实现步骤如下。

a.初始化大象种群、设最大迭代次数tmax，用适应度函数计算每个大象个体的适应度值，得到当前最优个体位置。

b.根据式(14)更新种群中每个大象个体的位置，使用式(15)、(16)更新当前最优个体的位置。计算更新之后的每个大象个体的适应度值，评估种群，得到更新后的种群最优和最差的大象个体位置。

c.将上一步得到的结果作为FF算法的初始值，设最大迭代次数kmax。

d.根据设定的种群大小，建立相应数量的萤火虫，在目标函数自变量的取值范围内随机确定每个萤火虫的位置。

e.对于最大化问题，评估过程中直接将目标作为亮度，对于最小化问题，则对目标值取相反数或倒数。之后再对萤火虫按照亮度进行排序，以确定当前种群中最优的个体。

f.亮度较低的萤火虫飞向亮度较高的萤火虫，亮度最亮的萤火虫随机移动。循环执行步骤d-f，直到迭代次数k达到设定的最大迭代次数kmax。

g.使用式(17)更新当前最差个体位置，保留更好的解。判断迭代次数t是否达到最大迭代次数tmax，若是，则输出当前最优个体位置及对应的适应度值，否则返回执行步骤b。

2.2 FF算法搜索行为研究进展

FF算法是原始的自然启发式算法，基于萤火虫的社会行为来解决连续多目标优化问题[22]，满足3个假设。

a.所有萤火虫都是单性的，即一只萤火虫会被其他萤火虫吸引；

b.吸引力依赖于亮度大小，即较不明亮的萤火虫会被较明亮的萤火虫吸引；

c.将萤火虫亮度设定为目标函数。

FF算法用来管理滤波元件和降低系统的谐波失真。从系统输入得到误差电压值、误差变化量及等效输出，降噪值根据输出值确定。FF算法存在2个关键点，即光强I变化和吸引力β[23]。当光吸收系数γ固定时，光强随距离r变化如式(18)所示。

I(r)=I0e-γr2

(18)

式中：I0为r=0时的光强。

考虑萤火虫的吸引力与相邻萤火虫看到的光强成正比，对其吸引力描述如式(19)所示。

β(r)=β0e-γr2

(19)

式中：β0为r=0时的吸引力。

任意2只萤火虫i和j在xi和xj处的距离如式(20)所示。

(20)

式中：xi,d为第i只萤火虫空间坐标xi的第d个分量；xj,d为第j只萤火虫空间坐标xj的第d个分量；D为问题维度。

萤火虫i向比萤火虫j更有吸引力(更明亮)的另一只萤火虫移动，如式(21)所示。

(21)

式中：α为随机参数；k为迭代次数；ψi为高斯分布或均匀分布的随机数向量。

优化过程取决于萤火虫亮度和萤火虫向更亮同类的移动。

3 结果分析

3.1 仿真分析

为验证智能控制器有效性，采用基准IEEE 30母线系统，拓扑图如图3所示。

系统由6台发电机组和41个支路组成，总负荷为283.4 MW，126.2 Mvar。首先，计算每条线路的电压、功率损耗、有功功率和无功功率。其次，根据配电网无功损耗降低和电压增强的理论，采用EHO-FF算法将DG定位在最优位置[24]。最后，利用PSO和Bat等算法验证其有效性。

表1给出了各种优化算法对不同参数的取值。

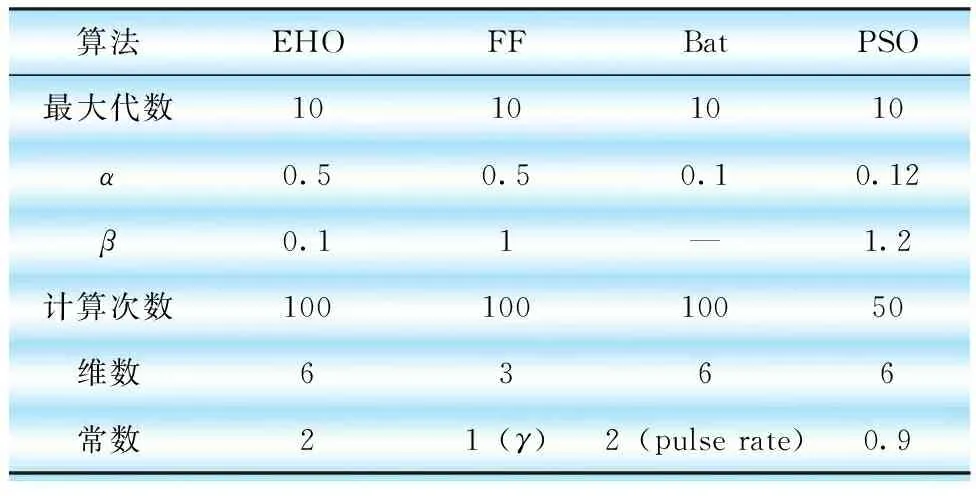
表1 算法参数

考虑一天中随机变化的24 h负载模式，如图4所示。首先，用Newton-Raphson法对IEEE 30系统的基本负荷进行程序运行，得到母线电压幅值、有功功率、无功功率、负载潮流见表2。

表2 Newton-Raphson法求解IEEE 30系统的潮流

从潮流出发，对各支路的电流和损耗进行计算。总有功功率为297.663 MW，无功功率为153.944 Mvar。由表2中得到的发电总负荷和线损结果可知，有功和无功功率均满足负荷平衡方程。

将DG单元放在发电机母线处(DG1在母线1处，DG2在母线2处，DG3在母线5处，DG4在母线8处，DG5在母线11处，DG6在母线13处)。利用PSO算法获得不同负载下DG单元的最优规模，如图3所示。表3给出了利用PSO算法布置与未布置DG时得到的总实际功率损耗。

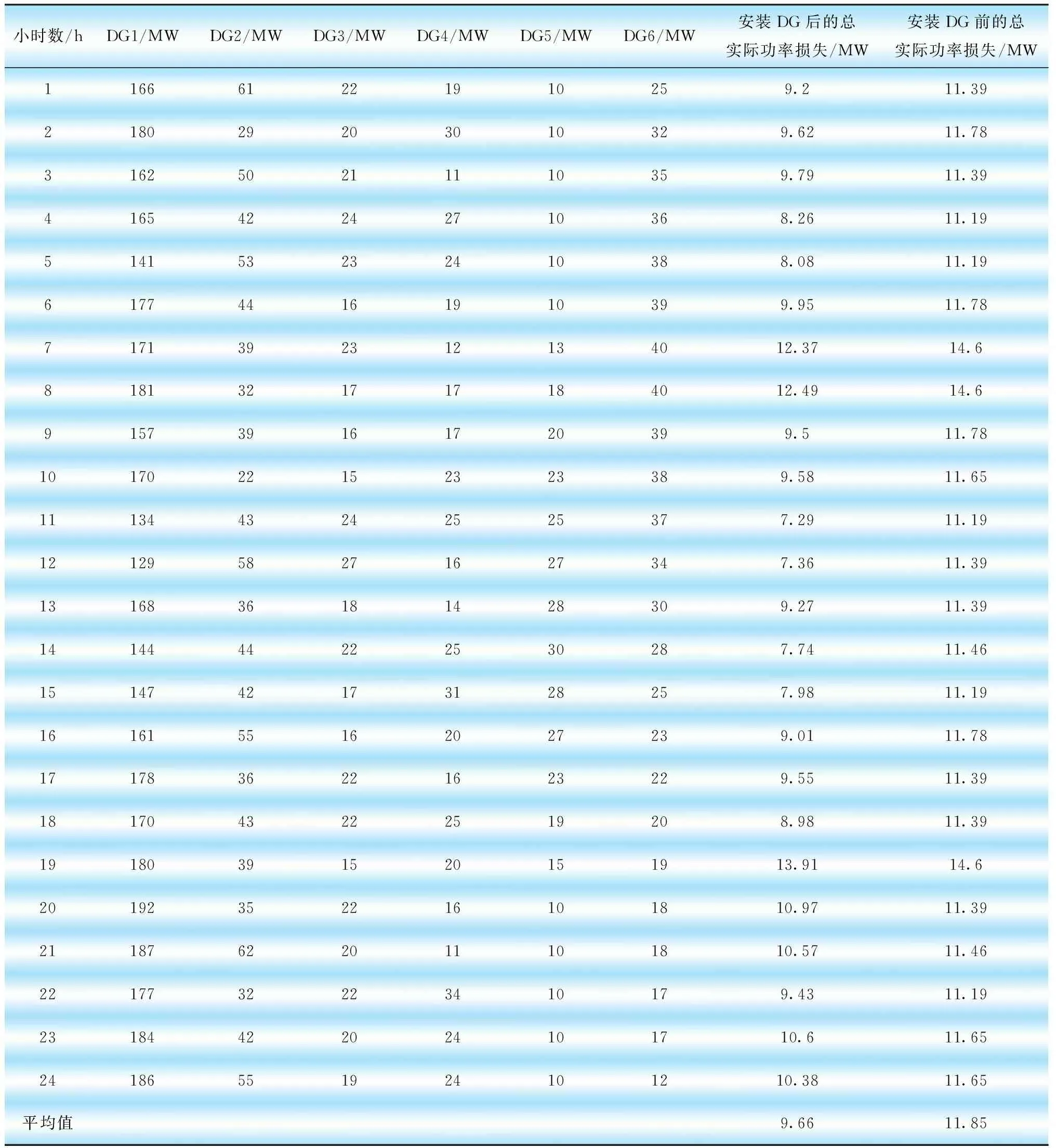
表3 PSO算法分析随DG变化负荷需求的功率损耗

采用PSO算法的IEEE 30母线系统在基本负荷下，实际功率损耗和无功功率损耗分别为10.886 MW和43.074 Mvar。布置最佳规模的DG机组后，每个负荷的实际功率损耗和无功功率损耗

如表3所示。无DG时平均实际功率损耗为11.85 MW，有DG时平均实际功率损耗为9.66 MW。因此，在确定位置以适当规模布置DG后，实际功率损耗降低。

同样，利用Bat算法获得不同负荷下，PSO算法已考虑过的放置在识别位置的DG单元的最优规模，如图3所示。通过计算，IEEE 30母线系统在基本负荷条件下的线路损耗为8.556 MW和34.389 Mvar。以最佳规模布置DG单元后，对每个负荷下的功率损耗进行计算，结果如表4所示。无DG时的实际平均功率损耗为11.4592 MW，有DG时的实际平均功率损耗为7.3971 MW。因此，在确定位置以适当规模布置DG后，平均实际功率损耗降低。与PSO算法的结果对比，发现Bat算法在考虑所有负载情况下均能降低实际损耗和无功损耗的平均值。

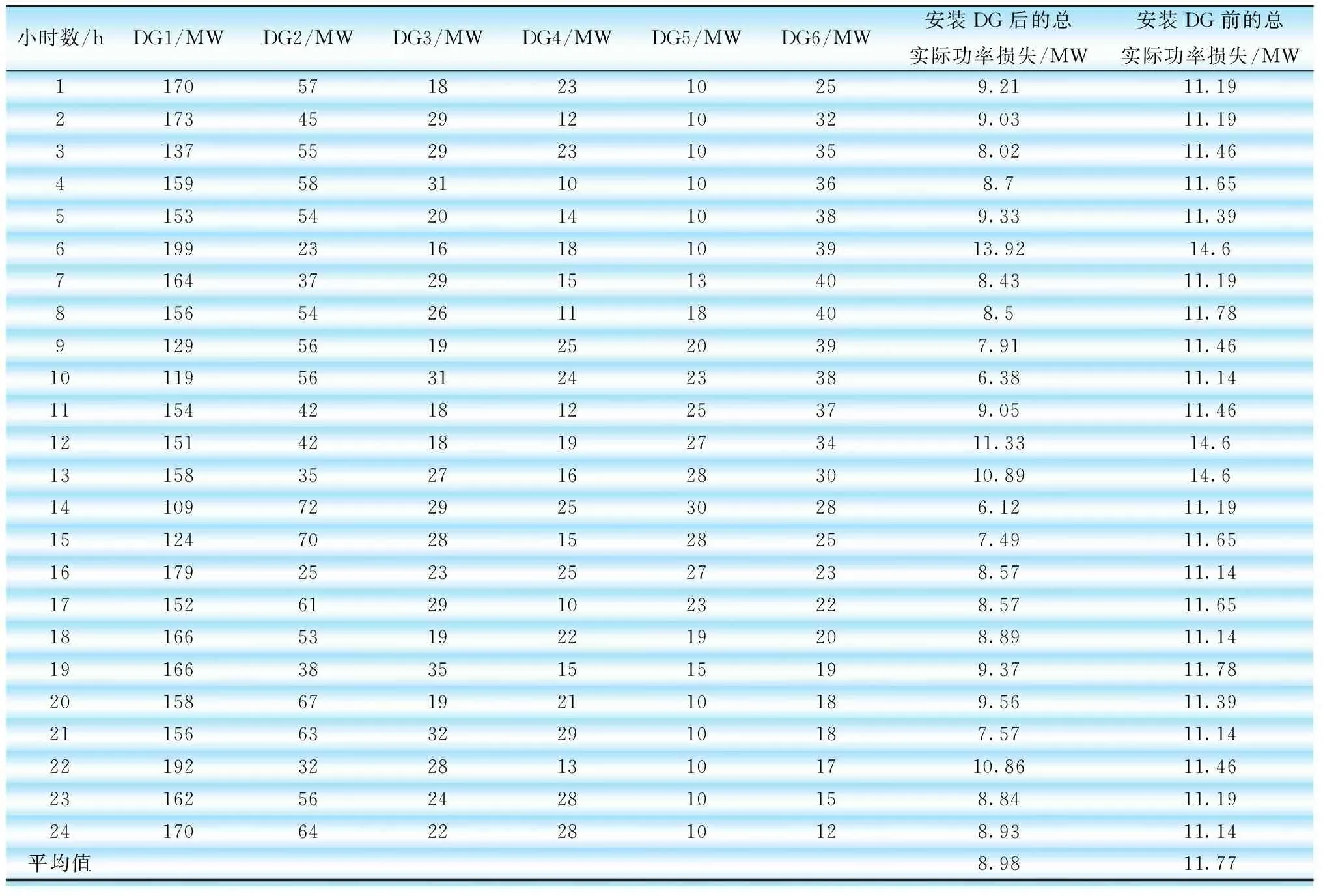
表4 Bat算法分析不同负荷下随DG变化的功率损耗

将EHO-FF算法应用于布置有DG的IEEE 30系统，模拟各种负荷下DG单元的最优规模，结果如表5所示。与PSO算法和Bat算法相比，未布置DG的情况下平均功耗降低到11.4592 MW，布置DG后平均功耗降低到7.3971 MW。

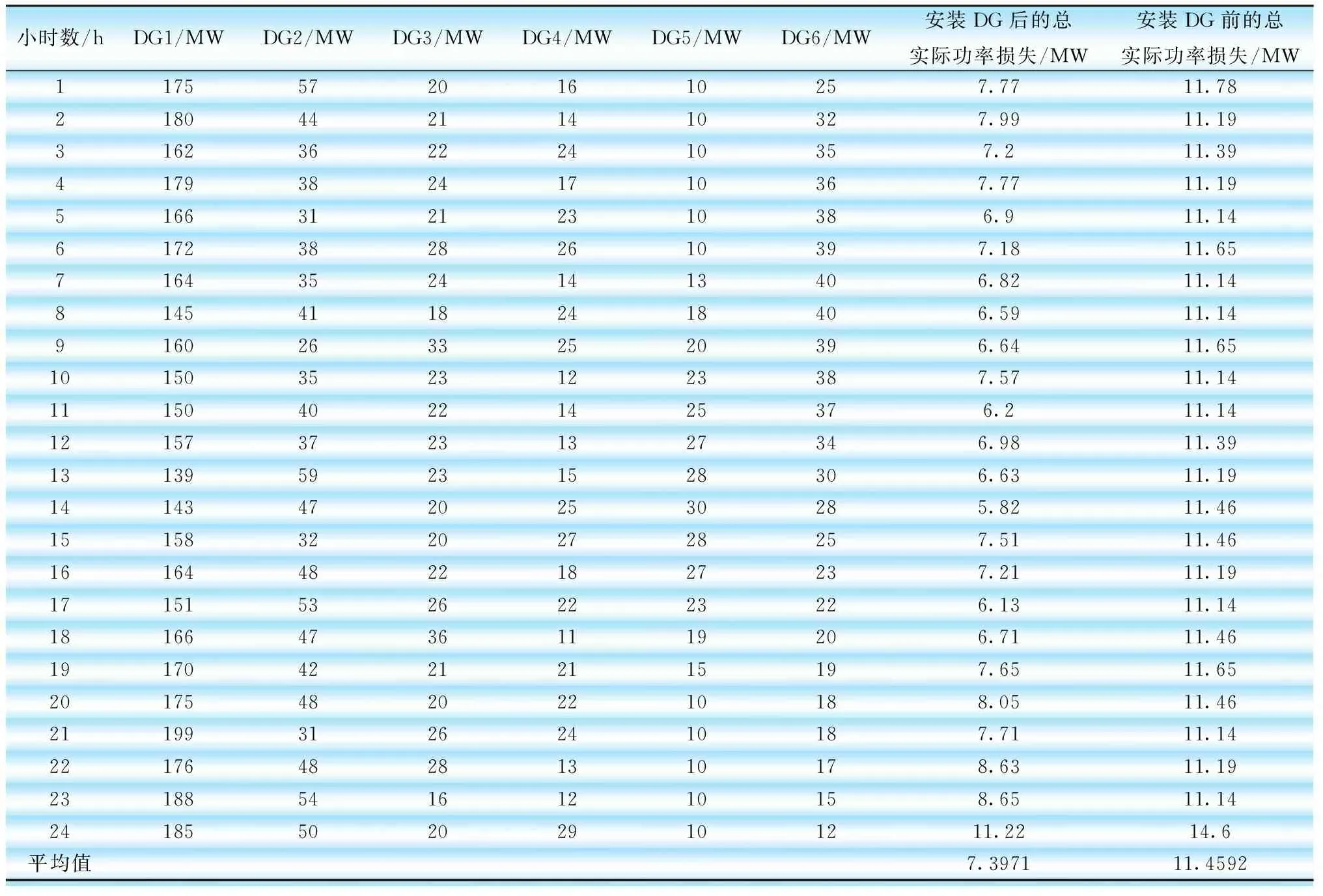
表5 EHO-FF算法分析不同负荷下随DG变化的功率损耗

PSO算法、Bat算法及EHO-FF算法的收敛性如图5所示。可以看出，EHO-FF算法与其他算法相比，收敛速度更快，迭代次数最少，能得到最优解。证明所提出EHO-FF算法的有效性和可行性。

3.2 不同算法结果比较

IEEE30系统在未布置与布置DG单元，采用Newton-Raphson、PSO、Bat和EHO-FF算法的结果对比分析如表6所示。基本负载情况下，EHO-FF算法的实际功率损耗和无功功率损耗都是最小的。布置DG单元后与其他算法相比，实际功率损耗也最小。

表6 IEEE 30系统未布置与布置DG单元的比较分析

根据各种优化算法的收敛结果，得出系统各母线处的电压分布。不同算法得到的电压分布如图6(a)所示。由图6(a)可知，与其他算法相比，EHO-FF算法可改善母线的电压分布，平均电压分布为1.02 pu。

系统中布置DG时，24 h实际总功率损耗如图6(b)所示。由图6(b)可知，采用EHO-FF算法的实际功率损耗明显降低。由表6可看出，EHO-FF算法的总实际功率损耗平均指标为7.39 MW，与其他算法相比有所降低。

综上所述，提出的EHO-FF算法优于其他算法，并通过试验更有效地优化智能电网的无功功率，提高不同电力企业的需求响应。

4 结语

本研究提出了针对智能电网无功优化的EHO-FF算法，将其描述为包含所有约束的优化问题，并与PSO、Bat等算法进行比较。结果表明，所提出的EHO-FF算法能最大限度地降低实际功率损耗，并显著改善系统的电压分布，在满足约束条件和节省时间方面具有优势。本研究仅涉及智能电网的损耗降低与改善电压分布，未考虑生产成本、DG成本等。下一步研究方向尝试由EHO-FF算法来解决包括各种成本函数及其相关约束的优化问题。