一种轻量型YOLO v3行人检测方法
2022-10-15李岩孟令军
李岩,孟令军
(中北大学, 电子测试技术国防科技重点实验室, 山西, 太原 030051)
0 引言
随着深度神经网络目标检测算法的发展,神经网络结构越来越复杂,权重参数量大幅度增加。当网络被部署到移动端设备时,庞大的模型导致加载时间长,参数占用计算机资源较多,对目标预测推理较慢,达不到实时性的要求。因此对模型压缩和加速的研究有重大意义[1]。对模型的压缩研究主要分为2个方向。
(1) 压缩已有网络,如HOWARD A G等[2]在模型构建阶段选择紧凑网络设计。MAO H Z等[3]利用1、2 bit代替来32 bit所表示的权重位数,牺牲精度降低模型权重大小。LIN X F等[4]删除网络不重要的权值,重新微调整个网络。
(2) 构建新的小网络,如HINTON G等[5]利用复杂的网络模型指导简单网络的训练,得到精度较高的简单模型结构。
本文采用压缩已有网络的方法,将YOLO v3-SPP[6-7]目标检测算法应用于行人图像的目标检测任务中,为了能够将模型更好的部署到移动端设备,对网络进行初始训练,得到预稀疏模型。将预稀疏模型进行稀疏训练,得到稀疏模型,对模型冗余的卷积层通道和残差结构剪枝,减少模型的权重,降低模型的运浮点算次数,提高模型的推理速度,得到一个轻量化的行人检测模型。
1 算法检测原理
如图1所示,YOLO v3-SPP由卷积层和残差结构堆叠而成,残差结构包括卷积层和残差层[8]。在模型训练阶段,将数据集中行人图像送入网络,经过不同大小卷积核的卷积层和残差结构,训练网络中参数权重,输出3个不同尺度的特征图[9],利用锚框匹配的方法在3个特征图对行人目标位置、类别、置信度进行预测,获取行人目标预测框与真实框的交并比,回归行人目标的位置损失和分类损失,调整神经网络中卷积层的权重,经过行人数据集的多次迭代,得到一个精度较高的行人检测模型[10]。在行人预测阶段,将待检测行人目标送入训练好的网络权重,得到3个不同尺度的特征图。通过锚框匹配特征图,得到行人目标的预测框,过滤置信度低的预测框,将置信度最高预测框的位置、精度、类别输出,得到行人目标检测的结果[11]。
2 模型剪枝
2.1 稀疏训练
神经网络经过稀疏性训练,可以为卷积层中每个通道培训比例因子,描述卷积层通道的重要性。对YOLO v3-SPP来说,卷积层后的归一化层可以对卷积特征进行归一化,提高模型的收敛和泛化能力[12],公式为
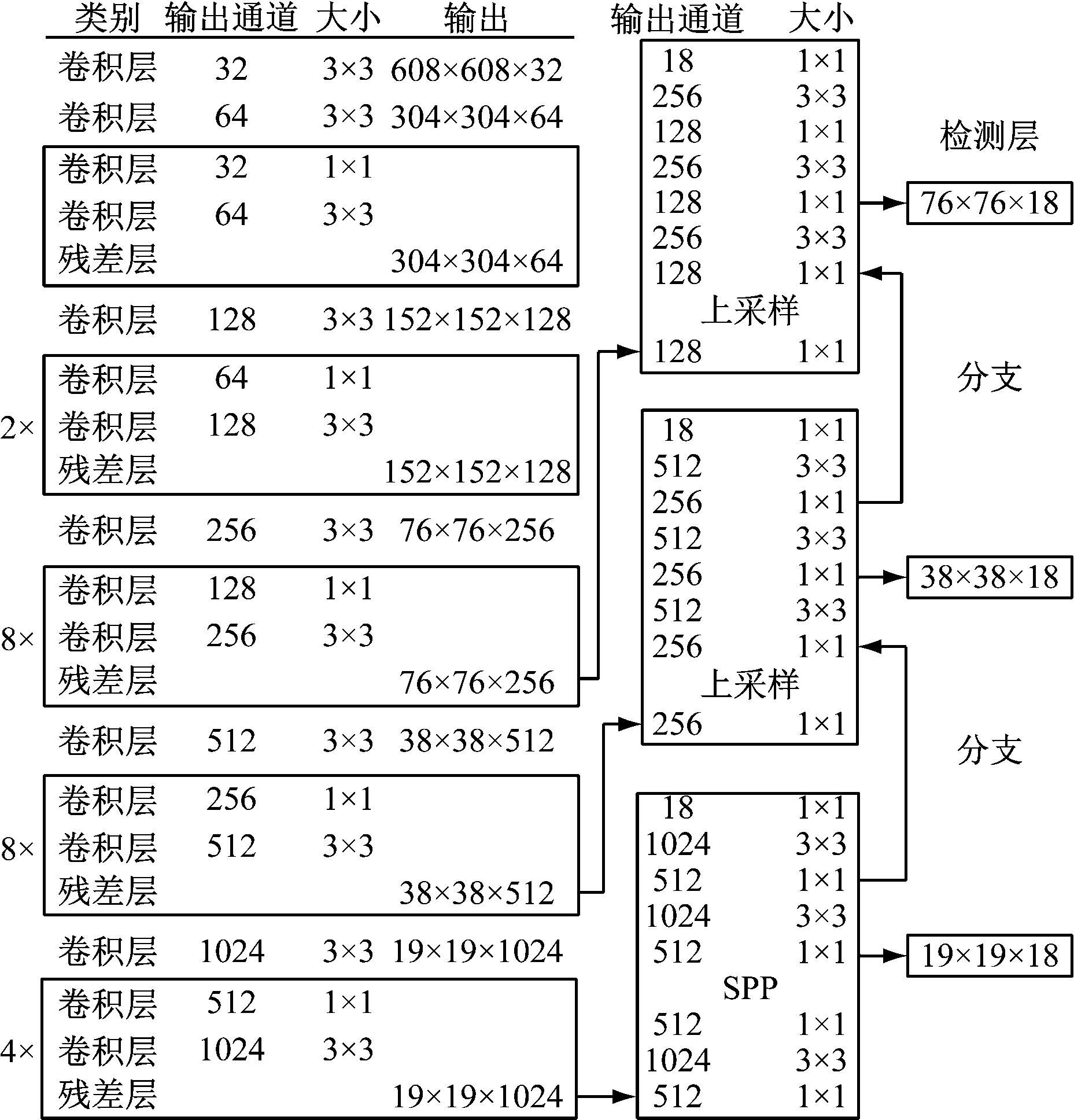
图1 YOLO v3网络结构图
(1)

(2)
当f(γ)=|γ|时,表示L1正则化,α表示平衡两个损失项的惩罚因子。实验中使用次梯度方法来优化非平滑L1的惩罚项。
稀疏训练通过α给模型添加额外的梯度,大的α一般稀疏较快且精度下降较快,小的α一般稀疏较慢且精度下降缓慢。当神经网络设置较大的学习率,模型梯度下降的较快,可以加快稀疏过程。在模型稀疏后期可以通过设置小的学习率,使模型精度上升。稀疏训练就是平衡精度和稀疏度的关系,通过稀疏训练我们可以得到卷积层中各个通道的比例因子γ[14],如图2所示。
2.2 卷积层通道剪枝
经过稀疏训练得到每一个卷积层通道的γ绝对值,将γ绝对值进行排序,通过设置通道剪枝率,得到需要剪枝的通道数量,剪掉γ绝对值较低的通道[15],如图3所示。
同理,我们将所有残差结构中3×3卷积层后归一化层γ的绝对平均值进行排序,设置剪枝数量,剪掉γ绝对平均值较低的残差结构[16],如图4所示。

图2 稀疏网络

图3 通道剪枝网络

图4 层剪枝网络
2.3 算法流程
模型剪枝的算法流程,如图5所示。初始网络经过权重训练得到训练模型,训练模型经过稀疏训练得到各个卷积层及残差结构γ分布情况,设置通道剪枝率和需要剪掉残差结构的个数,得到剪枝后的模型,将剪枝模型进行微调训练得到压缩模型,将不同压缩率的剪枝模型进行对比分析,得到最优剪枝模型[17]。
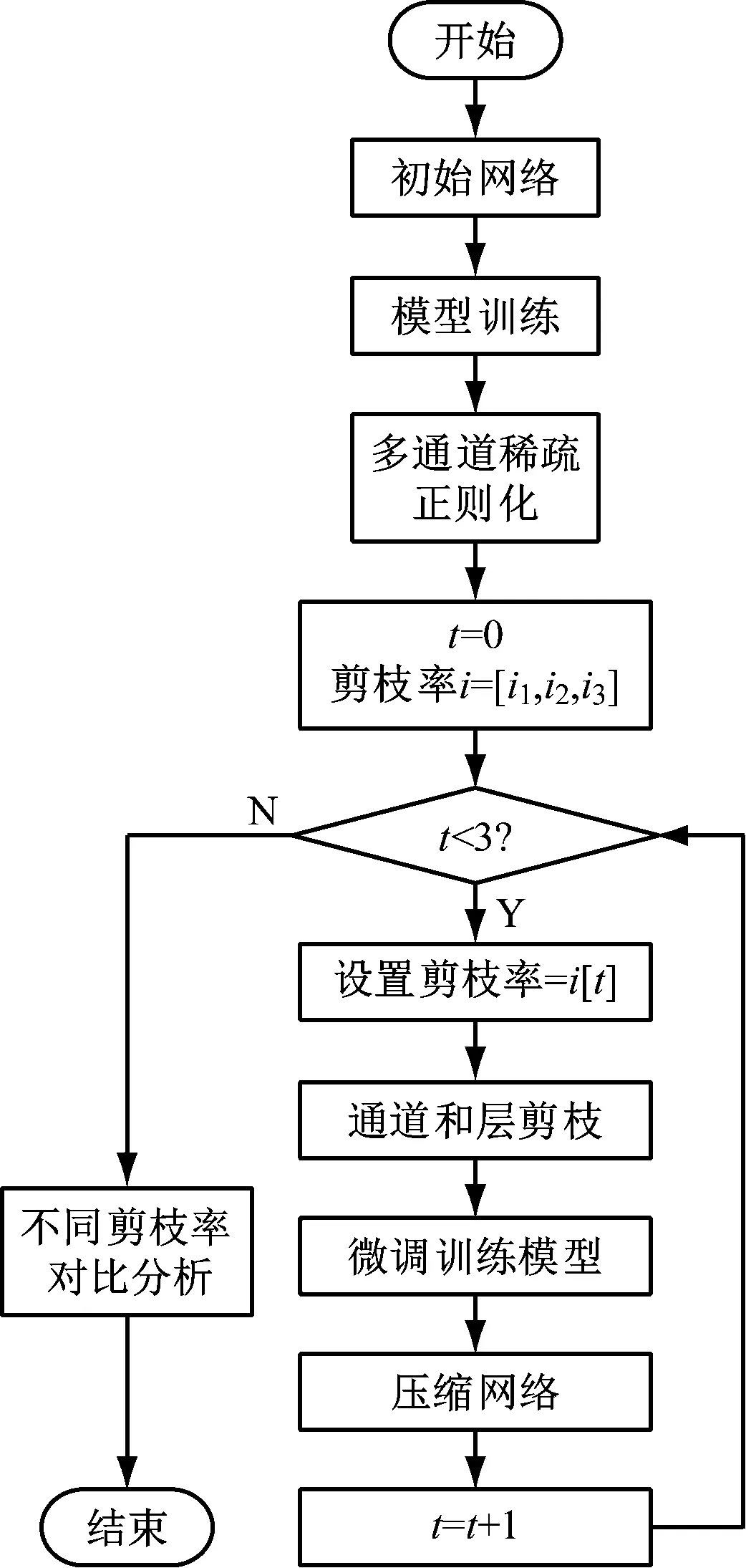
图5 模型剪枝算法流程
3 实验及结果分析
3.1 实验环境
为了验证剪枝后的模型在行人数据集的预测效果,全部实验在显卡为GTX1080Ti的平台上进行,该平台搭有PyTorch深度学习框架、CUDA加速库(GPU)。
3.2 模型训练
实验中输入图像尺寸为608×608,采用SGD优化器调节学习率。基础和稀疏训练的情况如图6所示,基础训练由于加载了初始权重,模型收敛较快,在中段已经出现过拟合现象,经过100Epochs迭代,最终得到基础模型的AP为0.891;稀疏训练加载基础训练模型权重,每次反向传播前,始终以恒定α0.001将L1正则化产生的梯度添加到归一化层的梯度中,并在epoch为210、290时降低学习率,设置γ为0.1。可以看到在模型稀疏的过程中,精度曲线波动较大,在学习率降低后,梯度下降减缓,模型精度得到了提高,最终经过稀疏训练的模型AP为0.866。

图6 基础和稀疏训练AP变化曲线
利用TensorBoard可视化工具,我们可以查看归一化层在基础和稀疏训练的情况。如图7所示,在基础训练的过程中γ分布在1左右,类似正态分布;在稀疏训练的过程中,随着稀疏训练次数的增加,γ分布在0附近,接近0的通道输出值近似于常量,可以将接近0的通道剪掉。

(a) 基础模型γ分布

(b) 稀疏模型γ分布
实验采用卷积层和通道同时剪枝的方式,将所有归一化层(不包括残差结构)通道的γ绝对值进行排序,设置剪枝率剪掉卷积层的通道。同理,对残差结构中3×3卷积层后BN层中所有通道γ的绝对平均值进行排序,剪掉平均值较低的残差结构。
3.3 对比实验
选取0.95、0.93、0.85、0.75、0.65五种剪枝率对模型通道进行剪枝,同时剪掉16个残差结构(32个卷积层,16个残差层)。模型经历不同剪枝率的剪枝后,权重大小分别压缩到了3.69 MB、5.295 MB、9.66 MB、15.5 MB、26.8 MB;参数量分别减少了98.5%、97.9%、96.2%、93.6%、88.8%;推理时间从18.3 ms降低到8.5 ms;但是模型精度出现了不同程度的下跌,分别为0.004、0.000、0.360、0.168、0.365,如表1所示。
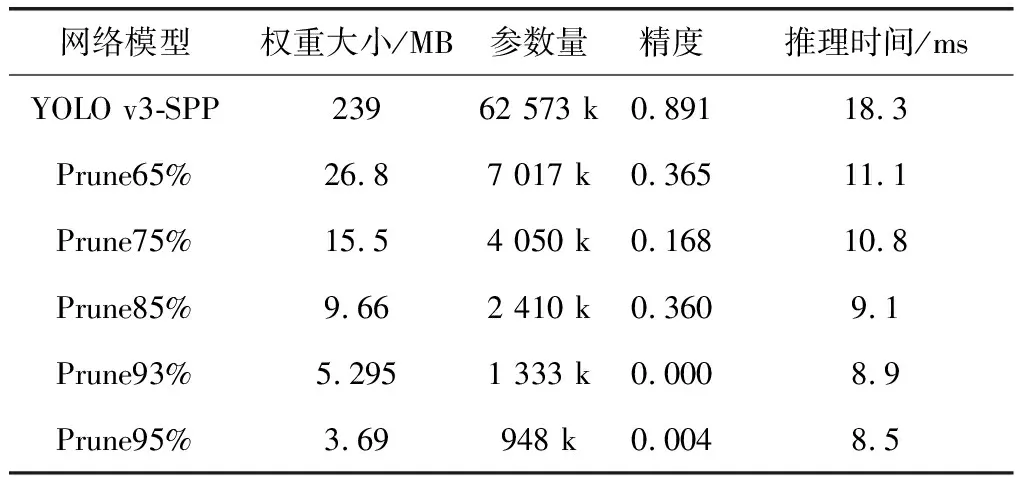
表1 不同剪枝策略测试结果
稀疏训练后,对不同剪枝率下的模型通过,50Epochs的微调,模型精度分别回升到0.808、0.847、0.868、0.866、0.868,如图8所示。

图8 微调模型后的准确率
通过表4和图8可以看到,当剪枝率为0.95和0.93时,剪枝模型的初始精度接近于0,但是通过50Epochs的微调后,精度依然可以回升到0.808和0.848,我们可以得出结论,经过通道和残差结构剪枝得到的模型是相对于数据集和初始模型得到的合理结构,保留的权重可以让剪枝模型快速接近这个结构的上限。同时,提高模型的剪枝率可以大幅度减少模型参数量,加快模型的推理速度;降低模型的剪枝率可以提高模型的精度,加快模型的推理速度。
通过5种不同剪枝率模型的比较,当剪枝率在0.75~0.93区间内有较高的精度,且模型权重较小。在区间内进行间隔取样,并进行模型微调后得到如表2和图9测试结果。

表2 0.75~0.93剪枝策略微调测试结果

图9 0.75~0.93区间内微调模型后的准确率
当剪枝率为0.88时,剪枝模型在区间内较高的精度,同时推理速度相接近且较剪枝前降低了近一半,权重大小仅为8.82 MB。平衡了模型权重大小、精度和推理速度的关系,归一化层γ也趋近于正态分布,如图10所示。

图10 0.88剪枝率模型微调后γ分布
图11是剪枝率为0.88的模型结构,同剪枝前的模型进行比较,可以看到模型的输出通道大幅度减少,16个残差结构被剪掉,模型大部分压缩。
通过表3对0.88剪枝率模型与原始模型的复杂度进行比较分析,可以看到剪枝后的模型浮点运算量减少了98.8 GFLOPS,提高了模型的运行速度;当行人图像输入GPU显存占用相同时,模型前后向传播显存占用降低了1 170.34 MB,模型权重显存占用减少了230 MB,减少了资源占用,降低了移动端硬件部署的限制,更符合实际要求。
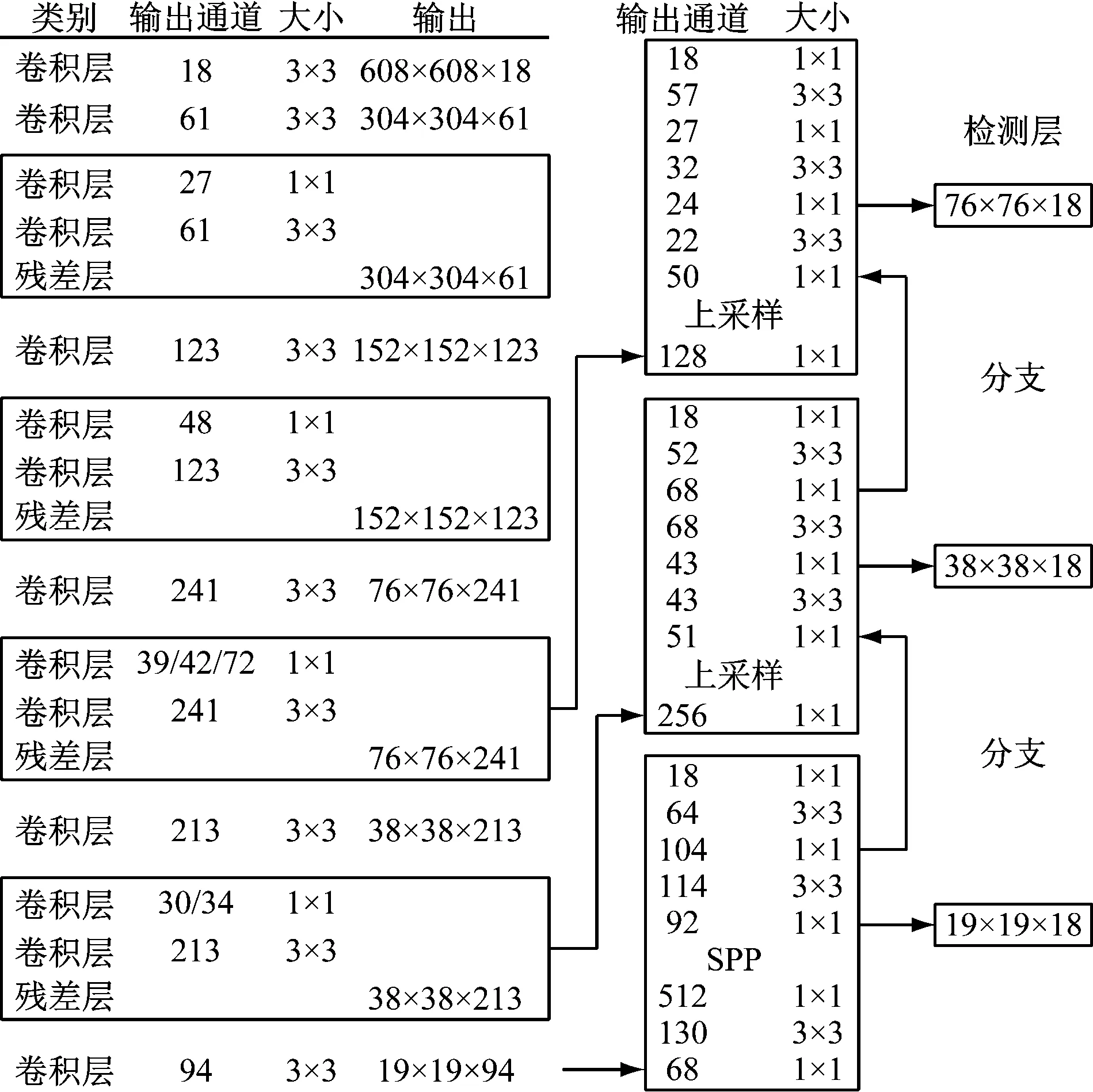
图11 0.88剪枝率的模型结构
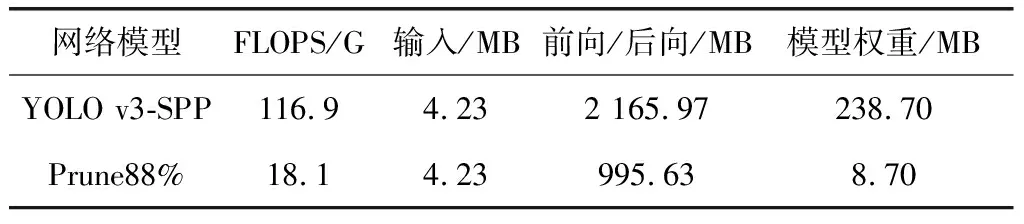
表3 复杂度对比
4 总结
为了更好的将行人检测模型部署到移动端设备,本文通过对卷积层通道和残差结构重要性进行分析,剪掉相应的通道和结构,降低硬件部署要求,减少计算机资源限制。实验结果表明,行人检测模型通过模型剪枝后,精度仅仅降低了2.2%,浮点运算次数降低了84.5%,前后向传播显存占用降低了54%,推理时间降低了50.4%,模型参数量减少了96.3%。下一步工作将利用TensorRT推理优化器,进行快速的部署和推理。
