小天体柔性附着状态协同估计方法
2022-10-15崔平远陆晓萱朱圣英梁子璇葛丹桐
崔平远,陆晓萱,朱圣英,梁子璇,葛丹桐
(1.北京理工大学深空探测技术研究所,北京 100081;2. 深空自主导航与控制工信部重点实验室,北京 100081)
0 引 言
小天体探测是人类探索生命起源、宇宙演化以及开发利用地外天体资源的有效途径,实现小天体表面安全附着则是开展小天体原位探测、采样返回等任务的必要前提。然而,小天体引力场弱且不规则、环境扰动复杂、表面形貌崎岖,为附着任务动力学精确建模以及安全附着导航制导方案设计带来挑战。此外,由于地面测控方式难以满足实时性需求,着陆器必须具备自主运行能力。而受制于星上有限控制精度,着陆速度与姿态往往与预期存在偏差,使得着陆器在附着时易发生倾覆、翻滚、反弹等现象,严重影响后续科学任务的开展。
目前人类已实施了五次小天体着陆(附着)采样任务,包括NASA的近地小行星交会(NEAR)任务,日本宇航局(JAXA)的隼鸟号(Hayabusa)任务、隼鸟2号(Hayabusa 2)任务,欧空局(ESA)的罗塞塔(Rosetta)任务,以及于2021年5月完成小行星表面采样的NASA OSIRIS-REx任务。其中,近地小行星交会(NEAR)探测器是首个成功绕飞小行星的探测器,最后以约2 m/s的速度撞落在Eros小行星上;另外四次任务,或是着陆时发生倾覆、反弹,导致探测器未能按计划成功着陆(隼鸟号、罗塞塔号);或是采用接触式采样模式,回避表面附着难题(隼鸟2号、冥王号)。然而,能否在小天体表面实现稳健着陆,直接影响着附着探测和采样返回任务的设计与实施。在小天体这类弱引力不确知星表环境中采用刚性着陆模式,要实现自主稳健着陆(即找到足够大小的平坦星表区域且着陆瞬间满足“双零”条件)是相当困难的。针对当前小天体刚性附着模式的局限性,亟需发展新型小天体附着模式,通过增强着陆器对复杂环境的适应能力以及对着陆状态偏差的容忍能力,实现高可靠、强适应的小天体表面着陆。
为此,本文提出“柔性附着”概念,创建小天体柔性附着模式,采用柔性着陆器实现小天体复杂形貌表面的稳健着陆。进而,针对柔性着陆器的状态估计问题展开研究,建立柔性着陆器近似模型,并提出柔性着陆器“等效面”概念及柔性着陆器姿态的近似表征方式。在此基础上,提出柔性附着状态协同估计方法,实现柔性着陆器的自主导航。
1 柔性附着问题描述
1.1 柔性附着模式
针对传统刚性着陆器在小天体附着过程中易倾覆反弹问题,以柔性着陆器取代刚性着陆器,采用柔性附着模式实现小天体表面着陆,柔性附着过程如图1所示。
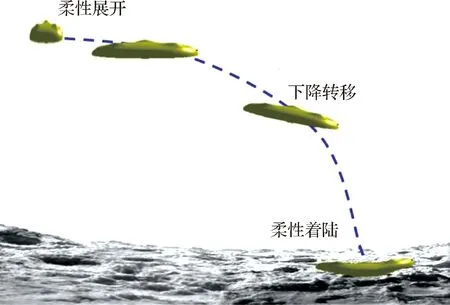
图1 小天体柔性附着过程Fig.1 The process of flexible landing on small celestial body
与刚性着陆器相比,柔性着陆器特有的柔性结构能够在着陆末端速度与姿态存在一定偏差情况下,通过增大与小天体表面接触面积,降低着陆器附着后发生倾覆翻滚的风险,并通过着陆器产生柔性形变,利用内部阻尼消耗剩余动能,从而避免着陆器发生反弹,提高小天体附着任务的可靠性。
1.2 柔性着陆器近似模型
柔性着陆器动力学特性复杂,属于分布参数系统,自主导航与控制系统难以设计。为此,在保留柔性特性的前提下,简化柔性着陆器结构,建立柔性着陆器近似模型,使其既具有柔性特性又能对其附着过程的状态进行估计和控制。
本文将柔性着陆器上具备特定功能、具有刚性特征的质量聚集区视为最小组成单元,柔性着陆器通过在质量聚集区上安装的导航敏感器和执行机构,实现自主导航和制导控制。质量聚集区之间存在柔性连接,在柔性连接约束下,质量聚集区之间的相对形变保持在一定范围内。对于具有面状外形的柔性着陆器,三质量聚集区模型是等效模拟柔性着陆器运动的最简配置,柔性着陆器的三质量聚集区近似模型如图2所示。
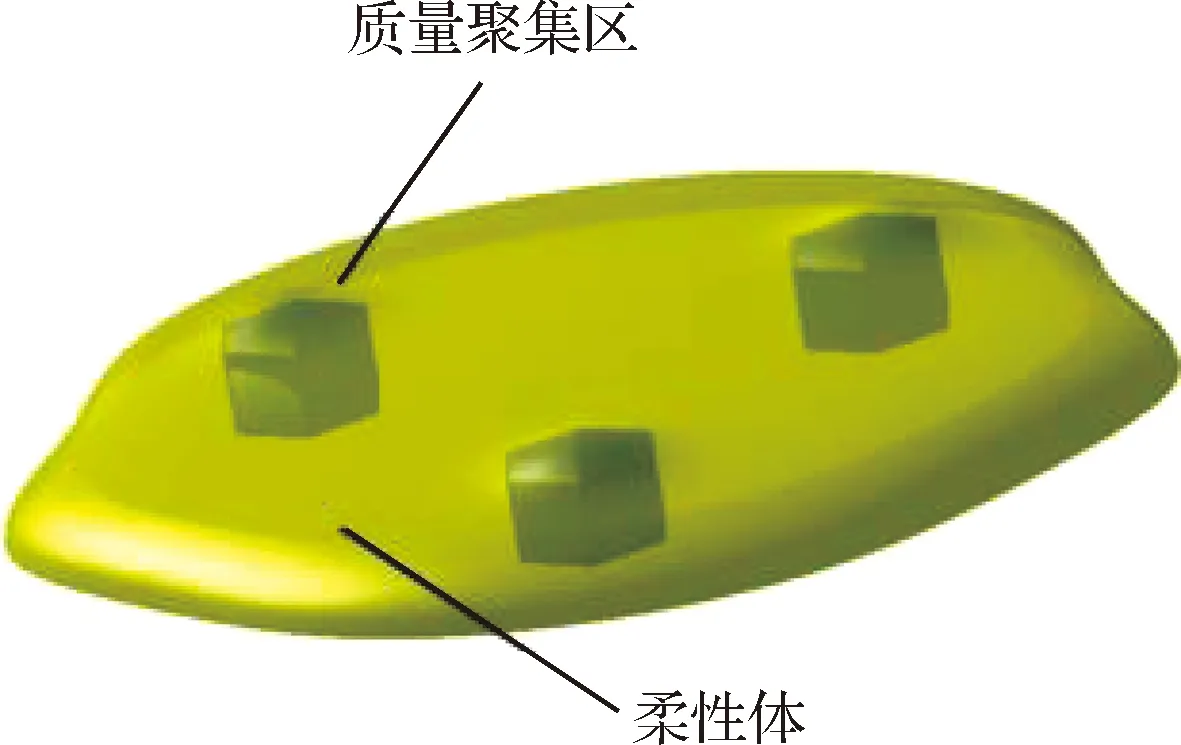
图2 柔性着陆器近似模型Fig.2 Approximate model of the flexible lander
为近似描述柔性着陆器状态,定义三个聚集区中心所在平面为柔性着陆器的“等效面”。用“等效面”的中心位置和速度近似表示柔性着陆器的位置和速度;同时定义柔性着陆器“等效面”与着陆平面的夹角为“等效面”倾角,用“等效面”倾角近似表征柔性着陆器的姿态。此处着陆平面指小天体附着点固连系的平面,如图3所示。其中,“等效面”的中心位置和速度分别通过三个质量聚集区中心构成三角形的形心位置和速度确定;“等效面”倾角反映了柔性着陆器相对着陆平面的水平程度,由柔性着陆器“等效面”法向量与着陆平面法向量间的夹角确定。

图3 柔性着陆器“等效面”示意图Fig.3 Illustration of the flexible lander’s “equivalent plane”
本文侧重于研究柔性着陆器状态估计问题。考虑到敏感器均布局在质量聚集区域,以下称质量聚集区为测量节点。
1.3 柔性附着状态估计问题
基于以上近似模型,柔性附着过程中,需要估计的状态量包括柔性着陆器“等效面”的中心位置、速度和倾角,以及测量节点的位置和速度。考虑到节点间受到柔性力作用,在附着点固连系下建立柔性着陆器节点动力学方程
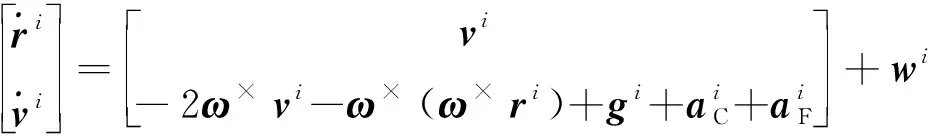
(1)
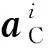
附着过程中,基于敏感器测量信息进行节点状态估计,通过多节点协同实现柔性着陆器的自主导航。本文考虑柔性着陆器测量节点安装惯性测量单元、激光测距仪和光学导航相机。假设敏感器坐标系与节点本体坐标系重合,记(=1,2,3)为节点本体坐标系,为小天体附着点固连坐标系,如图4所示。
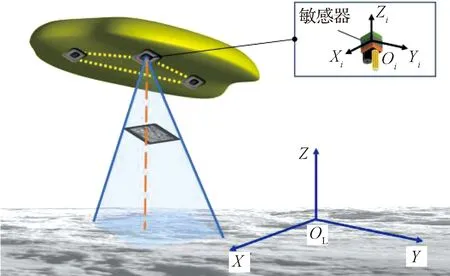
图4 坐标系定义Fig.4 Definition of the coordinate systems
与小天体刚性附着状态估计问题相比,多节点柔性附着状态估计存在的难点有:
1)柔性着陆器在附着过程中存在柔性形变、节点间运动状态强耦合,导致节点状态精确估计困难;
2)受着陆器尺寸限制,节点间距离较短,导致利用节点位置计算柔性着陆器姿态时,“等效面”倾角对节点位置估计误差敏感。
为此,本文提出一种适用于柔性附着的状态协同估计方法,利用柔性附着状态约束和节点间关联观测信息,提高节点状态估计精度,实现柔性着陆器的位置、速度和姿态估计。
2 柔性附着状态协同估计
柔性附着状态协同估计方法由节点状态独立估计、节点状态协同估计、柔性着陆器状态估计三个环节构成,如图5所示。
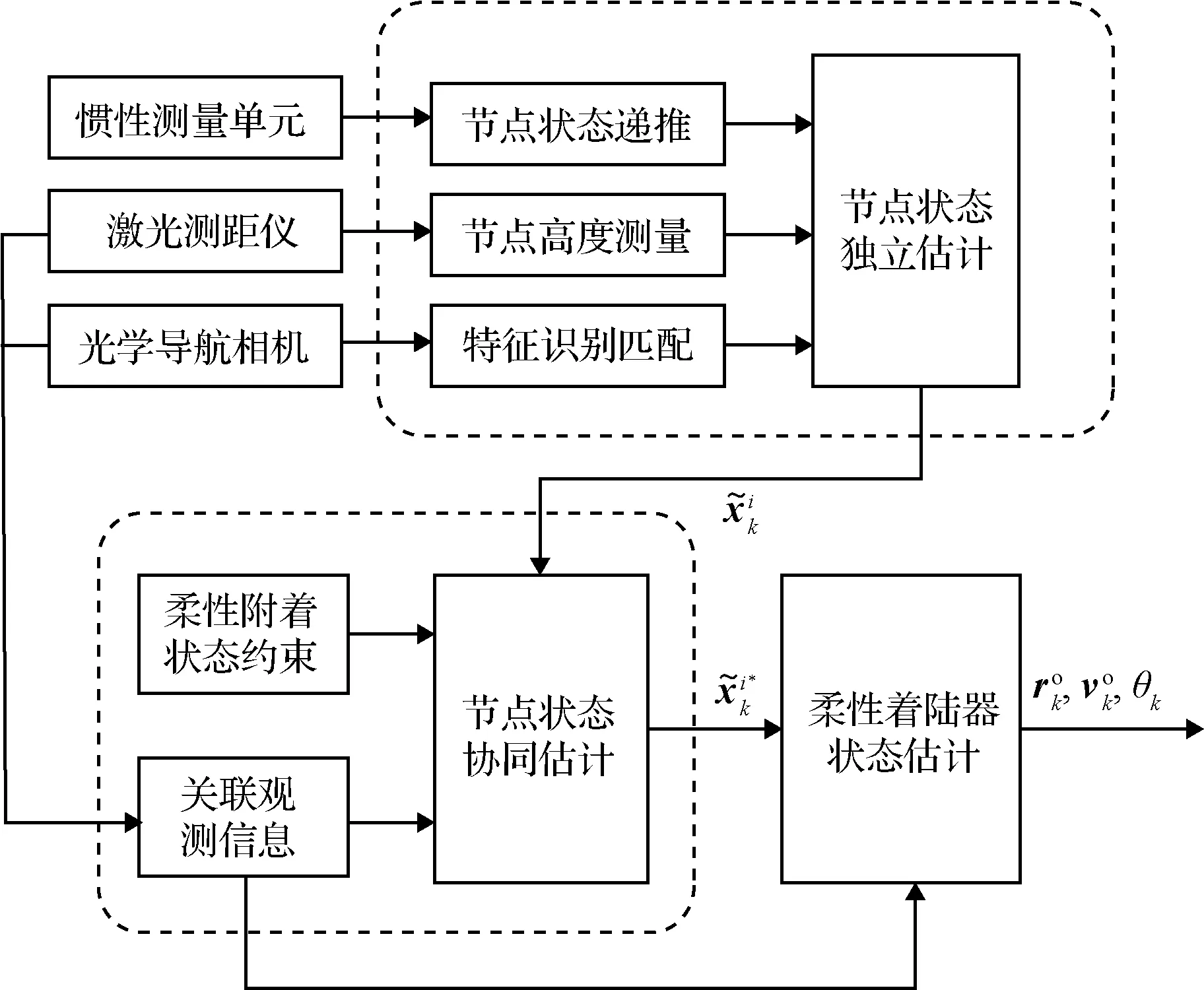
图5 柔性附着状态协同估计Fig.5 Cooperative state estimation for flexible landing
首先,利用惯性测量单元、激光测距仪和光学导航相机获取节点导航信息,实现节点状态独立估计;进而,引入柔性附着状态约束和节点间关联观测信息,通过多节点协同,提高节点状态估计精度;最后,根据节点状态确定柔性着陆器“等效面”的中心位置、速度和倾角,实现柔性着陆器的状态估计。
2.1 节点状态独立估计

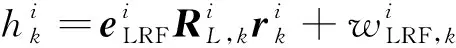
(2)
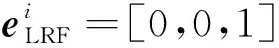
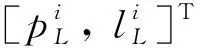
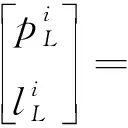
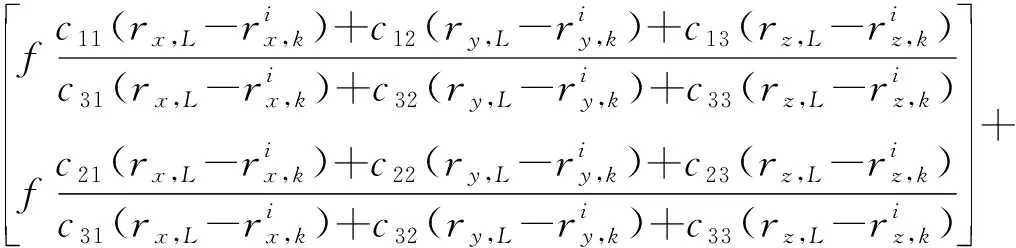
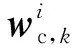
(3)
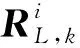
由式(1)-(3),建立节点状态方程和观测方程
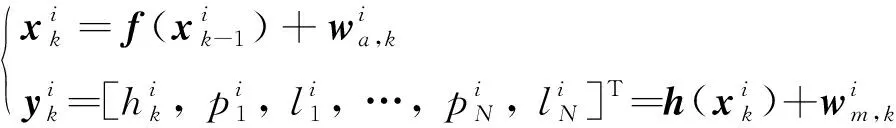
(4)
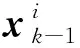
基于上述状态方程和观测方程,采用无迹卡尔曼滤波对节点状态进行独立估计:
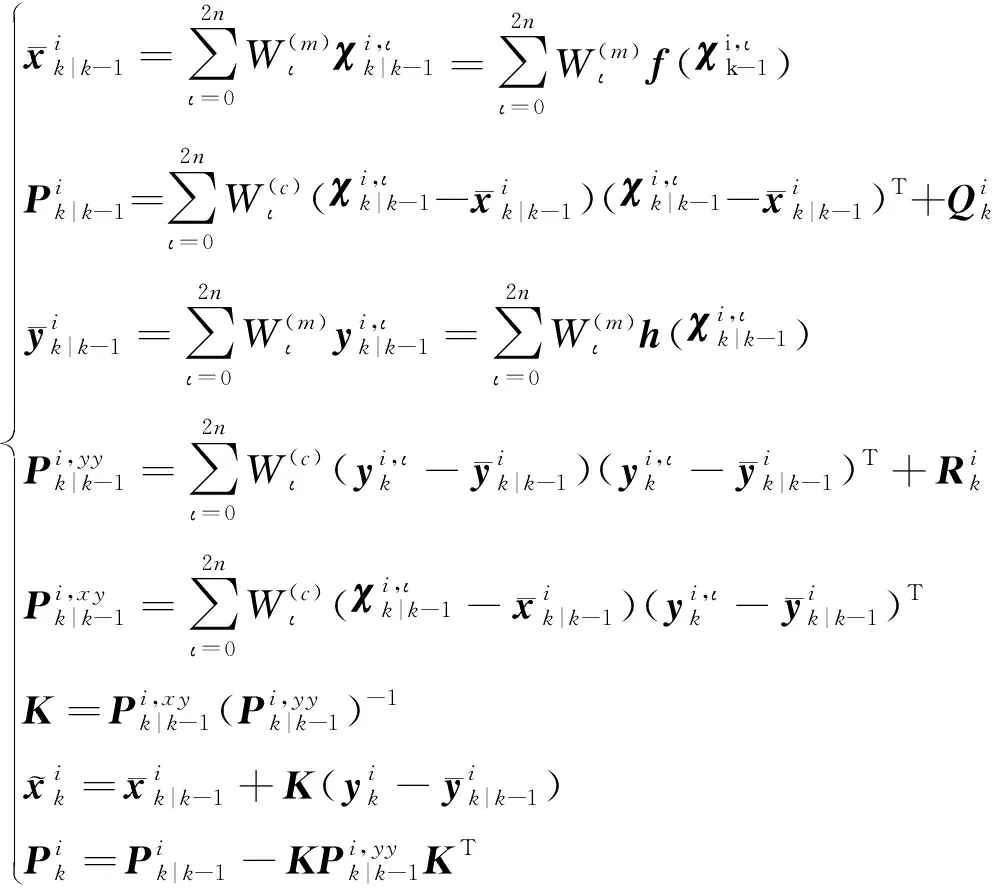
(5)
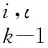
2.2 节点状态协同估计
柔性着陆器特有的柔性结构会导致节点间既产生柔性形变又受到柔性体约束,且附着过程中要求导航敏感器指向小天体表面。本节通过在节点状态估计中引入相应的柔性附着状态约束,修正状态估计误差。此外,当附着过程中不同节点存在关联观测信息时,可利用关联观测信息估计节点间相对位置,对节点状态进行协同修正,进一步提高节点状态的估计精度。
1)柔性附着状态约束
附着过程中,假设柔性着陆器因柔性形变导致的节点间相对距离满足
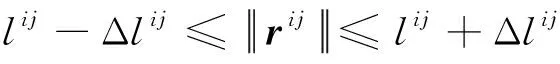
(6)
其中,为节点间标称相对距离,Δ为柔性体节点间的最大形变量。
此外,由于光学导航相机始终指向小天体表面,“等效面”法向量的轴分量始终为正,即
[()]>0
(7)
其中,=-,=-为节点间相对位置,=[0, 0, 1]为着陆平面法向量。
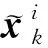
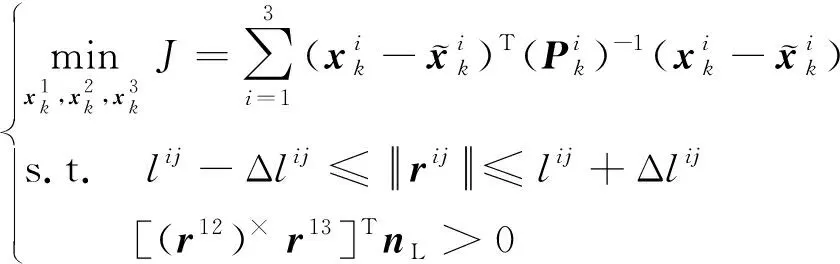
(8)
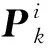
2)关联观测信息
当光学导航相机存在共同观测区域时,可基于重叠观测区域的特征匹配结果,获得节点间的关联观测信息,建立节点间对极约束方程
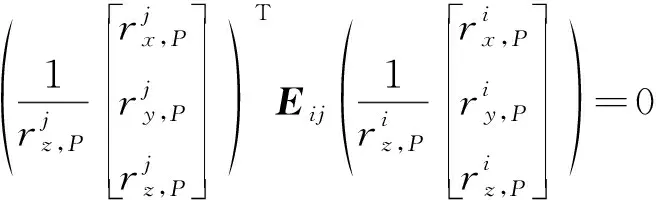
(9)
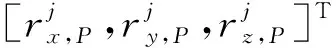
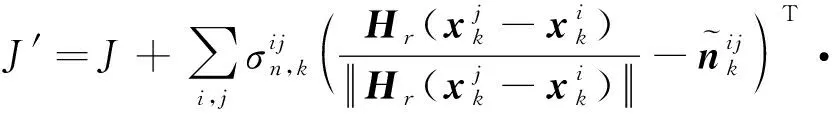
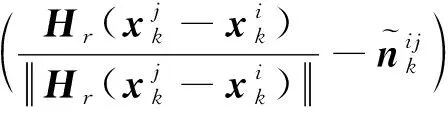
(10)
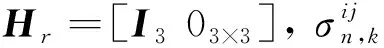
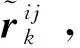

(11)
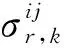
用增广指标′或″替换最小二乘问题(8)的指标,即可进行柔性附着状态约束和关联观测信息修正的节点状态协同估计。
2.3 柔性着陆器状态估计
根据1.2节的定义,利用三个节点的位置和速度,确定柔性着陆器“等效面”的中心位置、速度和倾角,实现柔性着陆器的状态估计。
柔性着陆器“等效面”的方程为
(-o)+(-o)+(-o)=0
(12)
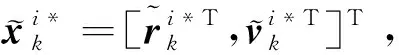
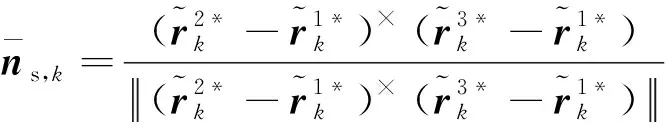
(13)
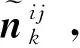
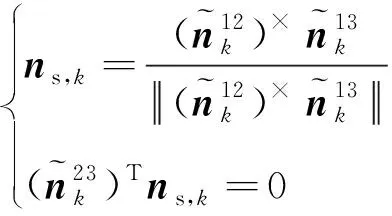
(14)
基于式(13)和式(14),估计“等效面”的法向量
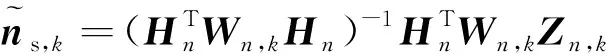
(15)
其中,,为权重,且
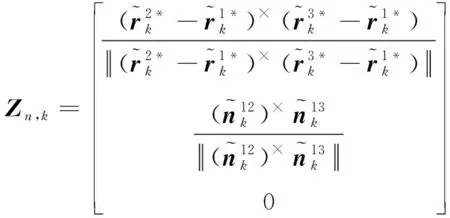
(16)
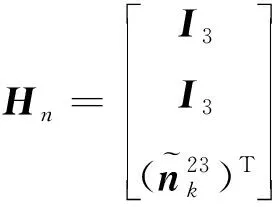
(17)
进而,结合着陆平面法向量,计算柔性着陆器“等效面”倾角:
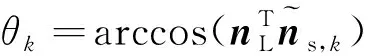
(18)
近似表征柔性着陆器的姿态。
3 数值仿真
本节对柔性附着状态协同估计方法进行仿真检验。假设柔性着陆器直径为3 m,标称状态下三个测量节点呈120°分布,节点与柔性着陆器“等效面”中心间距为0.75 m,节点初始与末端状态如表1所示。附着过程采用多项式制导,柔性着陆器“等效面”中心的运动轨迹如图6所示。
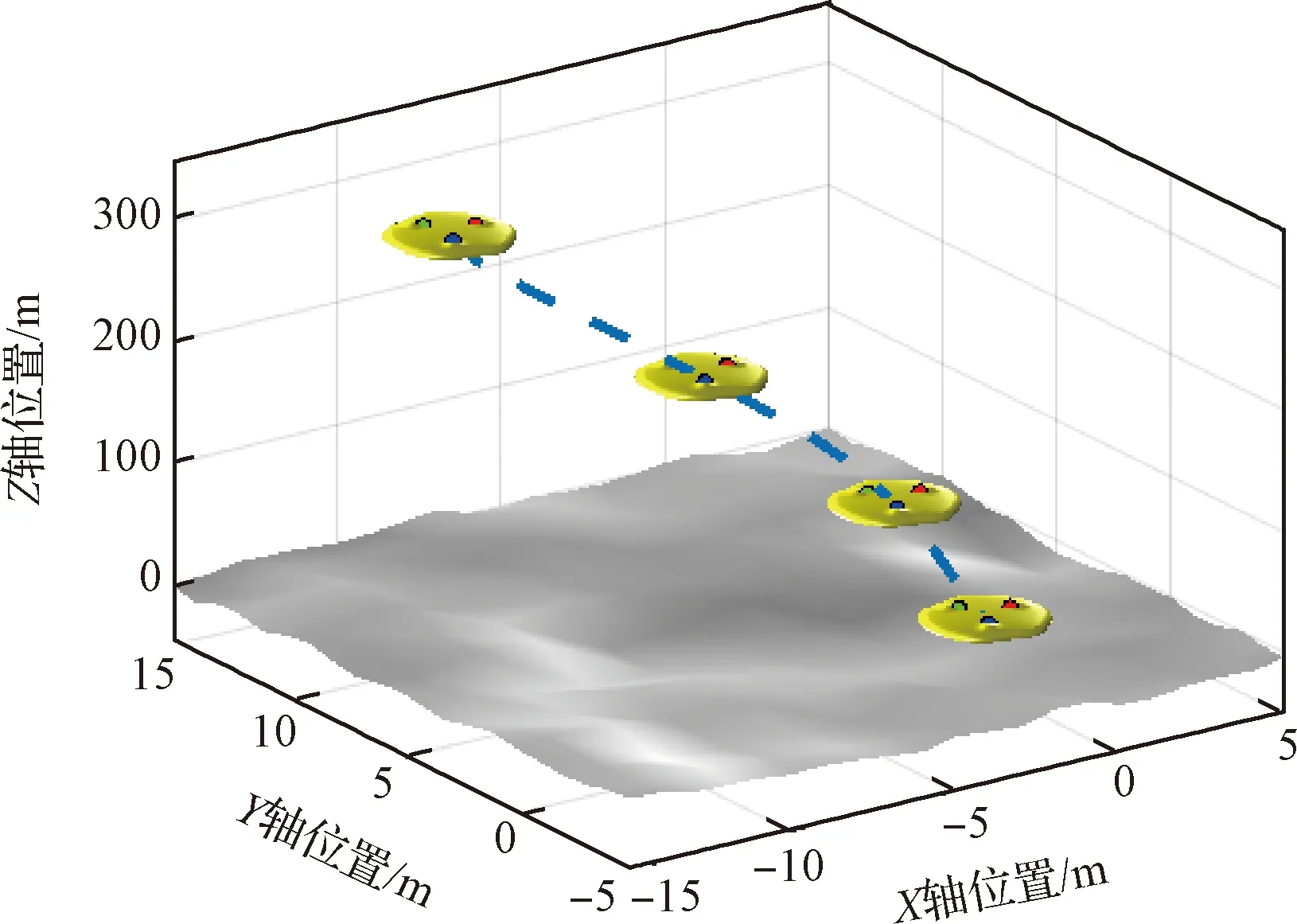
图6 柔性着陆器附着轨迹Fig.6 Landing trajectory of the flexible lander

表1 节点初始与末端状态Table 1 Initial and terminal states of the nodes
假设节点初始位置误差为[2,2,2]m,速度误差为[-0.1,-0.1,-0.1]m/s,导航敏感器参数如表2所示。利用柔性附着状态协同估计方法对节点状态和着陆器状态进行估计,结果如图7~9所示。
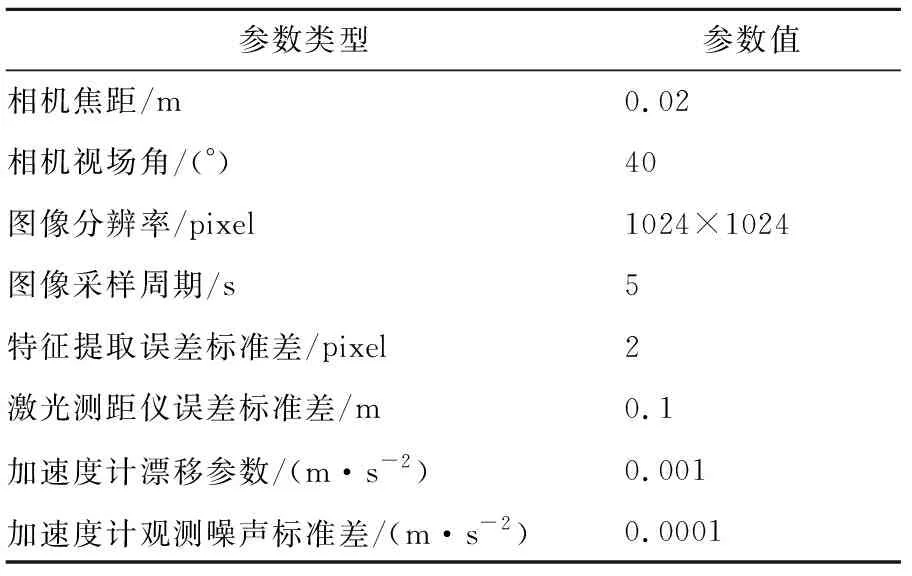
表2 导航敏感器参数Table 2 Parameters of the navigation sensors
假设节点间始终存在重叠观测区域,图7~8分别给出了节点位置和速度的估计误差曲线(节点1),其中黑色点画线(UKF)对应节点状态独立估计误差,红色虚线(UKF+约束)表示引入柔性附着状态约束后的状态估计误差,蓝色实线(UKF+约束+关联信息)为同时考虑节点间关联观测信息得到的节点状态协同估计误差。可以看出,引入柔性附着状态约束和节点间关联观测信息后,提高了节点状态估计精度。
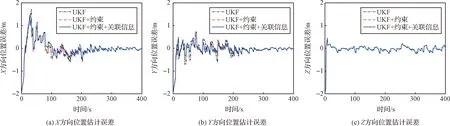
图7 节点位置估计误差(节点1)Fig.7 Estimation error of the node position (Node 1)
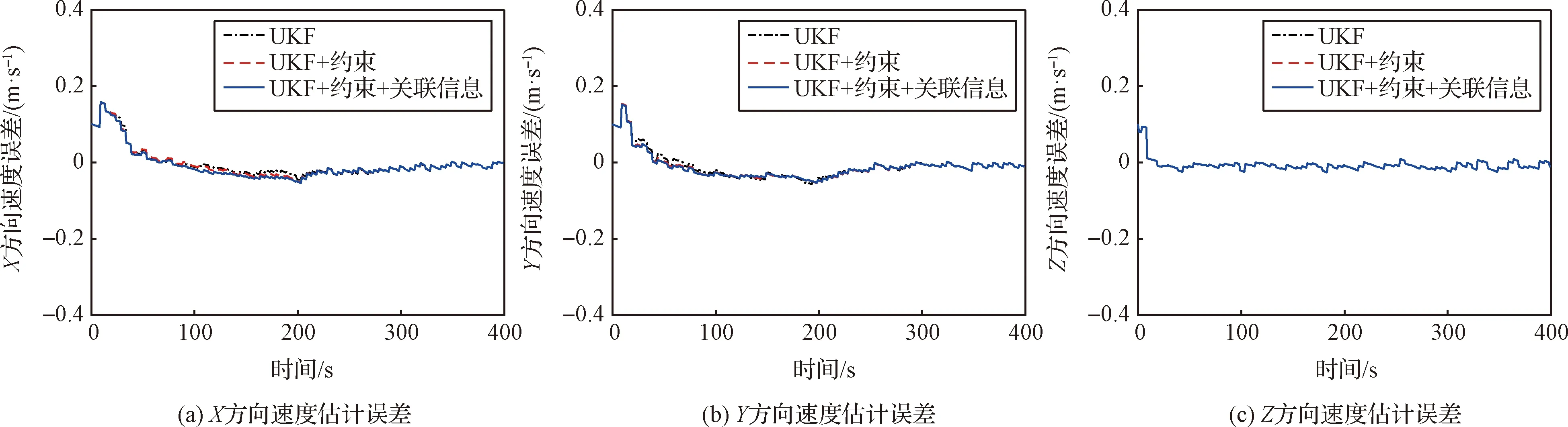
图8 节点速度估计误差(节点1)Fig.8 Estimation error of the node velocity (Node 1)
进而利用节点状态确定“等效面”的中心位置、速度和倾角,实现柔性着陆器的状态估计。图9(a)和9(b)分别给出了附着过程“等效面”中心位置和速度的估计误差曲线,其变化趋势与节点的位置和速度估计误差基本一致。图9(c)给出了“等效面”倾角的估计误差曲线,其中红色虚线为利用节点位置估计值得到的“等效面”倾角误差,蓝色实线表示引入节点间关联观测信息得到的“等效面”倾角误差。由仿真结果可以看到,同时利用节点位置和节点间关联观测信息估计“等效面”倾角,能够提高柔性着陆器的姿态估计精度。
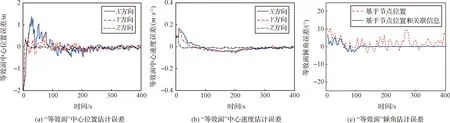
图9 柔性着陆器状态估计误差Fig.9 Estimation error of the flexible lander state
4 结 论
针对小天体附着过程,传统刚性着陆器易倾覆反弹导致任务失败问题,提出了“柔性附着”概念,研究了柔性着陆器附着过程的状态估计问题。在建立柔性着陆器近似模型、提出柔性着陆器“等效面”概念基础上,利用“等效面”的中心位置和速度近似表示柔性着陆器的位置和速度,同时采用“等效面”倾角近似表征柔性着陆器姿态,可以实现柔性着陆器附着过程的状态估计。所提出的柔性附着状态协同估计方法,通过利用柔性附着状态约束和节点间关联观测信息,可以提高柔性附着过程的节点状态估计精度,进而提高柔性着陆器位置、速度和姿态的估计精度。
