协同过滤推荐算法中的相似性度量研究

李散散，陈小荣

（广州工商学院 工学院，广东 广州 510850）

0 引 言

大数据时代用户获取信息越来越方便，同时用户也能感受到大数据技术带来的一些困扰，如信息过载出现的信息冗余和人们对信息的依赖性。举个生活中常见的例子，在电子商务领域，各类购物平台上陈列着不计其数的商品，用户可以借助搜索引擎查找自己感兴趣的商品，与此同时用户也常会遇到选择困难的情况，特别是在用户没有明确需求的情况下，这种困扰会更加明显。此时强大的搜索引擎也无计可施，不能很好地帮助用户筛选商品，就在此时推荐系统应运而生。推荐系统是一种可以借助一定的算法分析用户历史数据获取用户偏好和需求，然后主动推荐给用户感兴趣的信息，从而减少用户查找时间的工具。如，eBay的“兴趣购物”功能，可以根据购物者的浏览和购物行为，为每一个购物者提供用户行为画像，然后给用户打造一个私人订制的页面。这样一来电子商务平台就可以解决用户购物时需浏览大量无关信息和商品所带来的困扰，从而优化用户购物体验，实现精准营销。

1 协同过滤推荐算法概述

1.1 协同过滤算法基本原理

协同过滤推荐算法通常分为两种类型：基于用户的协同过滤算法和基于项目的协同过滤算法。该算法的基本思想是“物以类聚，人以群分”，主要是通过搜集用户在线上的历史记录数据，建立用户偏好模型。然后通过计算用户或项目之间的相似度来查找与目标用户相似的用户群或者目标用户可能感兴趣的项目。最后通过计算用户对项目的预测评分来生成推荐列表。下面以给用户推荐电影为例阐述该算法的原理，表1记录了5个用户对5部电影的评分情况，其中行是电影名，列是用户。从表格中的数据可以看出Tom、Bob和Lucy三个用户具有相似的兴趣偏好，因为他们三个对Léon、Supper man、Titanic三部电影有相同的评分，因此在给用户Lucy推荐电影时会推荐Jurassic park这部电影，即与用户Lucy相似度高的用户喜欢的而用户Lucy并没有观看的电影。而对于新用户Amy和新电影Homealone则无法进行推荐，因为评分很少或者没有评分，从而不能找到与其有一定相似度的用户或电影，这就是协同过滤推荐算法存在的用户冷启动和项目冷启动问题。即，不能给新用户做个性化推荐，也不能将新项目推荐给可能对它感兴趣的用户。

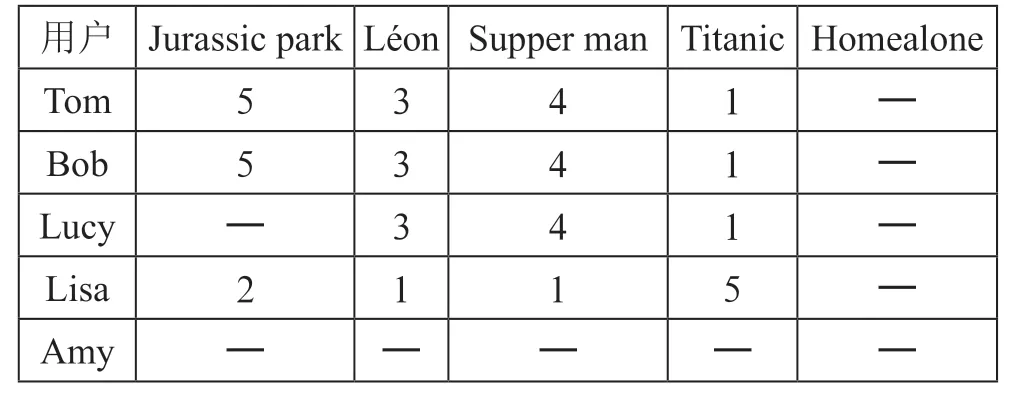
表1 用户—电影评分

1.2 协同过滤算法的实现过程

1.2.1 建立用户-项目评分矩阵

协同过滤推荐算法首先要收集用户偏好，这可以通过整理用户行为历史记录而得到，例如用户对项目的评分、投票、转发、评论、购买、点击、保存等。然后对用户行为预处理之后，形成二维矩阵，两个维度分别是用户列表和项目列表，值代表用户对项目的偏好。如图1所示，r表示用户对项目的评分，分值的大小表示用户对项目的喜欢程度，如果用户对项目没有评分，则记为0或者φ。这些无评分数据的元素占整个矩阵空间的比率就是该数据的稀疏度，数据的稀疏度对推荐质量有着直接的影响。例如：有个user、个item、共个评分，数据的稀疏度计算公式为：1－(/×)。

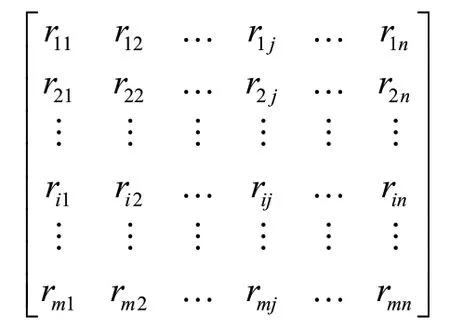
图1 用户—项目评分矩阵

1.2.2 计算相似度

关于相似度的计算，目前的方法基本都是通过计算两个向量的距离来衡量相似度的大小，距离越近越相似。例如，在图1的用户—项目评分矩阵中，我们可以将一个用户对所有项目的评分，即矩阵中的一行当作一个向量来计算不同用户之间的相似度，同理，也可以将所有用户对同一个项目的评分，即矩阵中的一列看作一个向量来计算不同项目之间的相似度。相似度的计算方法主要有以下几种：

（1）余弦相似度计算。余弦相似度是通过计算两个向量夹角的余弦值来衡量用户或项目之间的差异大小。当两个向量的夹角为0°时，余弦值为1，表明两个用户或项目的相似度最高。项目之间的相似度计算公式为：

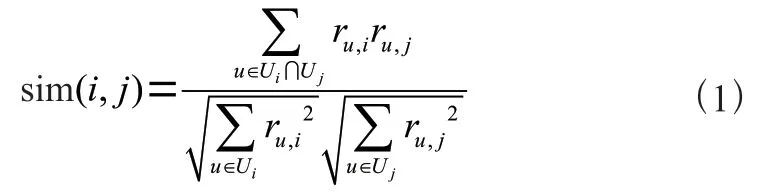
其中，U、U分别表示对项目和项目评分的用户集合，r,、r,分别表示用户对项目的评分、用户对项目的评分。

（2）修正的余弦相似度。余弦相似度主要是从方向上区分差异性，对绝对的数值不敏感，因而不能反映每个维度上数值的差异，这就导致结果的误差，需要修正。举个例子，用户对电影的评价（1～5分），两个用户A、B对两部电影的评分分别是（1，2）（4，5）。使用余弦相似度计算的结果是0.98，此数值表明这两个用户极为相似。但从具体的评分来看用户A似乎并不喜欢这两部电影，相对比，B用户则比较喜欢。

还有一种情况是，用户在给项目评分时，由于没有一个统一的评分准则，用户的打分尺度会因人而异。有些用户要求苛刻，整体打分可能偏低；而有些用户态度随和，整体打分偏高。这种用户态度引起的评分差异不利于构建合理有效的预测评分模型。因此，为了解决以上评分习惯的问题，引入用户在所有历史项目中的平均评分，得到以下公式：

（3）Pearson相关系数。Pearson相关系数反映了两个变量之间的线性相关性，在推荐场景中计算的是对项目和项目都参与评分的用户之间相似度。具体计算公式为：

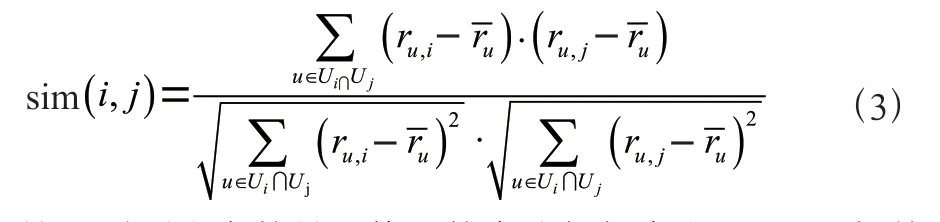
这里需要注意的是，修正的余弦相似度和Pearson相关系数在公式上存在细微差别，体现在公式的分母上。其中，修正的余弦相似度的分母是分别计算对项目或项目有过评分的用户，Pearson相关系数的分母则是计算对项目和项目均有评分的用户。

（4）本文改进的相似度计算方法。项目的热门程度或用户活跃度对相似度的计算有一定的影响，可以假设，衡量用户之间相似度时，有以下两种情况：即，1）两个用户对某热门项目有较高评分；2）这两个用户对某冷门项目有同样评分。我们可以判定第二种情况更能说明这两个用户具有相似的偏好。同理，活跃用户对项目相似度的贡献应该也小于不活跃的用户。基于这个观点，我们在计算项目之间相似度时加入log(1+())来对用户活跃度做一定惩罚，修正后的项目相似度计算公式为：

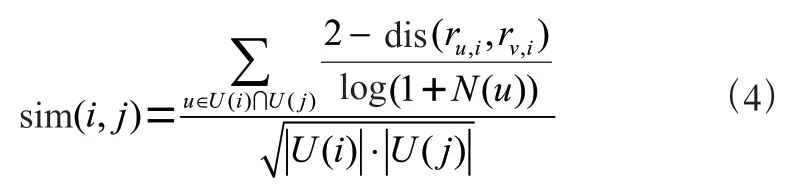
其中，()是用户评过分的项目集合，()表示对项目评分的用户集合，r表示用户对项目的评分，dis计算的是两个评分的绝对值差。

1.2.3 生成推荐列表

利用上述相似度计算方法计算每个项目和目标项目的相似度后，对这些相似度进行从高到低排序，筛选相似度最高的（最邻近的）个项目，即候选集。

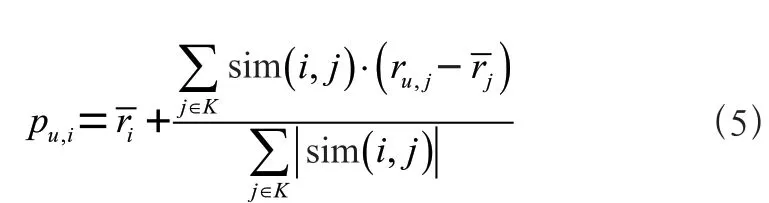
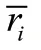
2 实验过程与结果

2.1 数据集

本文使用基于项目的协同过滤推荐算法开展实验。本实验的数据集是某电商网站用户订单数据集，该数据集包括用户信息和购买产品信息，我们将用户购买商品的次数转化为用户评分，评分值为1～5分。具体转化的原则是：如果用户A购买商品的次数为1，则记为用户A对商品的评分为1分，以此类推，当用户购买商品的次数达到5次则为5分，分值越高表示用户对商品的喜欢程度越高。本实验选取的数据集包含610个用户对9 724个商品的100 836条评分。为了更好地评价模型，我们随机将数据集划分成训练集和测试集，比例为3:1，训练集用来产生实验结果，测试集用来验证实验结果。

2.2 实验流程

步骤1：建立用户-项目评分矩阵。

步骤2：通过相似度计算方法，找到邻近项目。

步骤3：采用TOP-N法对候选集中项目相似度进行排序，得到和项目最相似的前个项目集合。

步骤4：对最邻近的个项目进行用户评分预测。

步骤5：根据预测评分值与用户评分平均值的关系，生成推荐列表。

2.3 评价指标

在完成实验之后我们利用一些常用度量指标评价推荐系统预测的准确性，例如，均方根误差、召回率和准确率。以下为具体的定义和公式。

2.3.1 均方根误差

均方根误差（RMSE），它是通过计算若干个预测值和真实值偏差的平方和与观测次数的比值的平方根对预测效果进行综合评价。均方根误差对于一组测量中特大或特小误差比较敏感，所以它能够很好地反映出测量的精准度。具体计算公式如式（6）。其中，是观测次数，p是预测值，r是真实值，从公式可以看出RMSE的取值与推荐质量成反比。

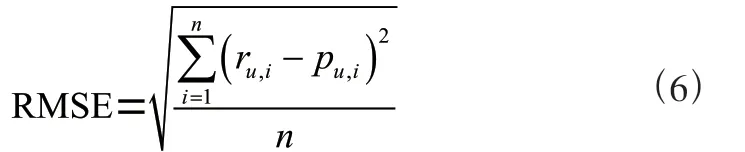
2.3.2 召回率

召回率（Recall）表示推荐列表中有多少被真实预测到了，是推荐列表中用户喜欢的项目数量与用户所有喜欢的项目的比值。它能够直接反映出推荐结果的精准度，计算公式如式（7）。其中，R和T分别表示给用户推荐的项目集合、用户真实喜欢的项目集合。

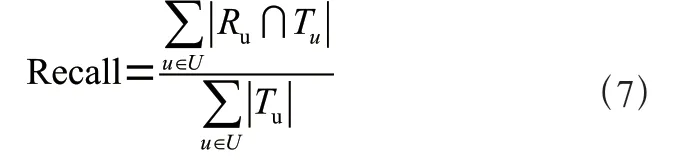
2.3.3 准确率

准确率（Precision）是指推荐系统给用户的推荐列表中用户实际选择的项目与所有被推荐项目的比例。计算公式为：

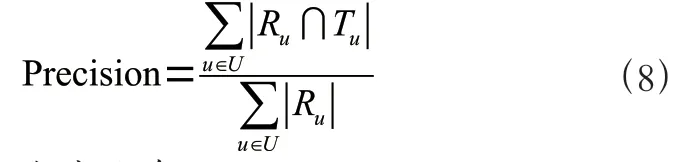
2.3.4 平均绝对误差

平均绝对误差（MAE）是指预测值和观测值之间绝对误差的平均值。MAE值越小，预测结果越准确，它的计算公式为式（9）。其中，r表示用户对项目的实际评分，p表示用户对项目的预测评分，为预测次数。

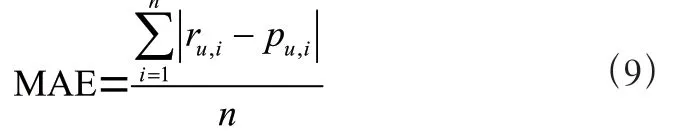
2.4 实验结果与分析

通过整理实验数据，我们得出四种相似性度量方法在推荐的准确率、召回率、均方根误差和平均绝对误差四个方面的差异，以及值（最近邻居数量）对推荐结果的影响。根据实验数据制作了图2至图5，如下所示。

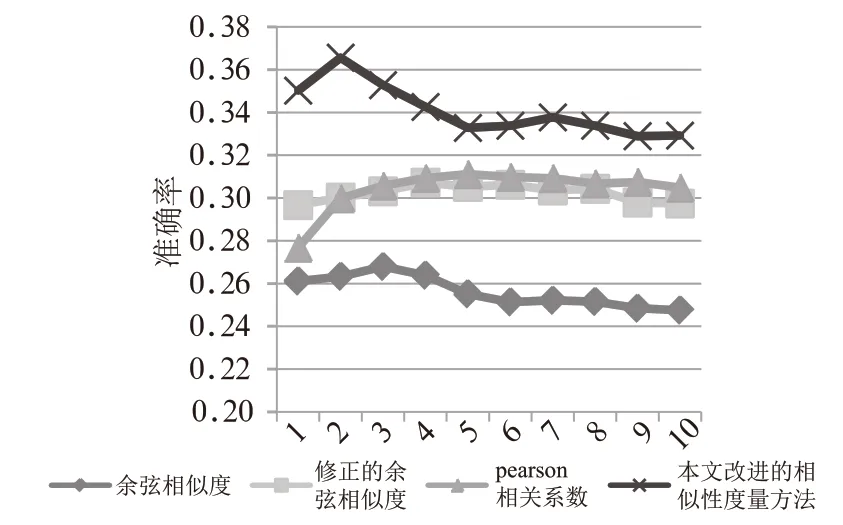
图2 不同相似度计算方法的准确率

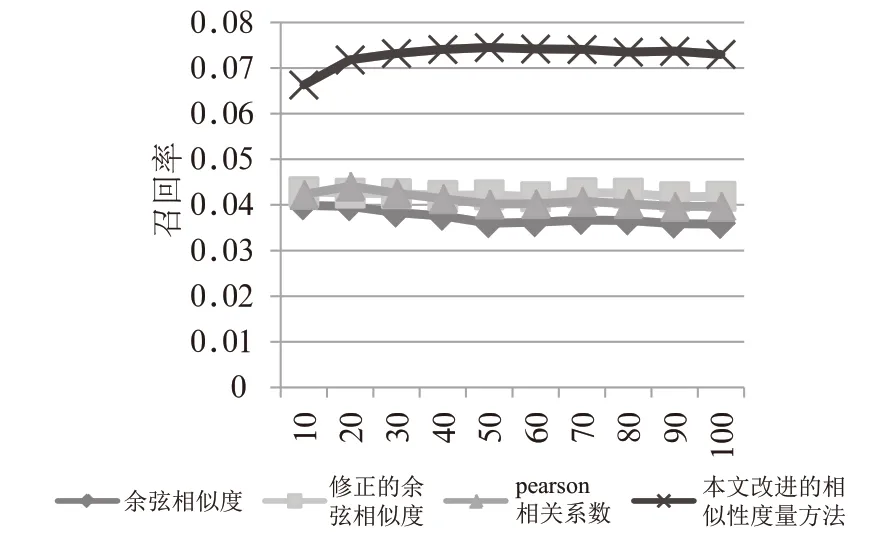
图3 不同相似度计算方法的召回率

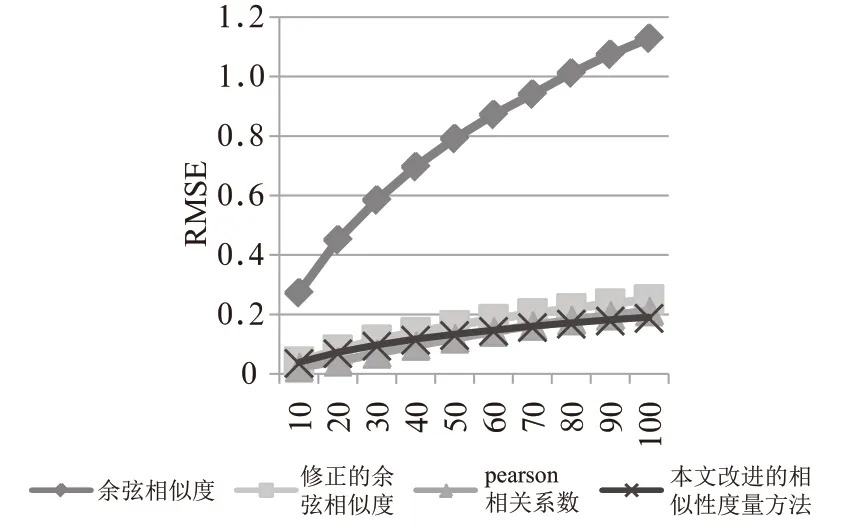
图4 不同相似度计算方法的均方根误差

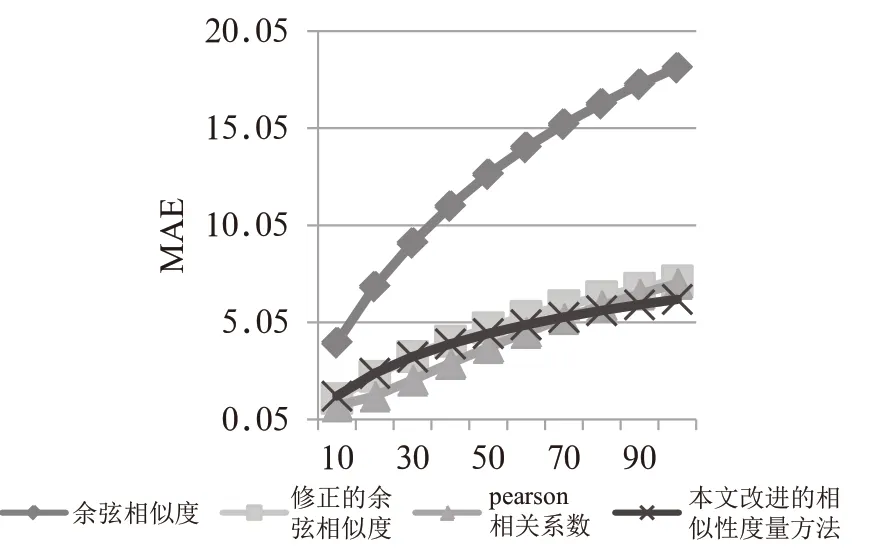
图5 不同相似度计算方法的平均绝对误差

2.4.1 实验结果

结果1：从图2和图3看，改进的相似度计算方法的准确率和召回率明显优于其他相似度计算方法，特别是相对于余弦相似度的方法而言。同时我们也发现修正的余弦相似度和Pearson相关系数的准确率和召回率较为接近。

结果2：对于不同最近邻居数量，即不同值（＝｛10，20，30，…，100｝）对推荐准确率、召回率、RMSE和MAE的影响。从图中可以看出，最近邻居数量对四种相似性度量方法的评价指标均有影响。其中对RMSE和MAE的影响较大，对召回率的影响最小。相比而言，最近邻居数量对修正的余弦相似度、Pearson相关系数和本文提出的改进的相似度计算方法的影响较小。

结果3：从图4和图5来看，4种方法的均方根误差和平均绝对误差整体会随着最近邻数量的增加有增加的趋势，余弦相似度的方法表现得更加明显。而修正的余弦相似度、Pearson相关系数和本文改进的相似度计算方法的RMSE和MAE比较接近，它们这3种方法的预测精准度明显比余弦相似度方法高，其中本文改进的相似度计算方法的数据更加稳定。

2.4.2 实验结果分析

实验结果显示本文提出的相似度计算方法在四个指标中均具有较好的表现，但效果不够显著，究其原因主要有以下两个因素：

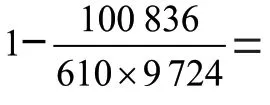
如何缓解数据稀疏性问题呢？很多研究者针对这一问题提出了改进的方法，主要可以归为三类：数据填充、聚类方法和矩阵分解。以数据填充方法为例，可以通过预测值填充的方法对未评分的项目填充数值，该方法主要从协同过滤推荐算法的两个分类出发，预测用户对未评分项目的评分。首先根据项目之间的相似度和用户对项目的个邻近项目的评分来预测对未评分项目的评分，然后将预测评分填充到项目—评分矩阵中，预测评分的计算公式见式（5）。如果出现用户对项目的个最邻近项目也未评分的情况，即r为空，则根据用户之间的相似度，以及与目标用户最邻近的个用户对项目的评分，来预测用户对项目的评分，然后将预测评分数据再次填充到矩阵中，计算公式见式（10）。将预测评分数据填充到矩阵后，再次进行项目之间相似度的计算，然后重新生成推荐列表。最近邻居数量的多少会影响最近邻居与目标用户或目标项目的相似度，因此在进行数据填充时值选择不宜过大。

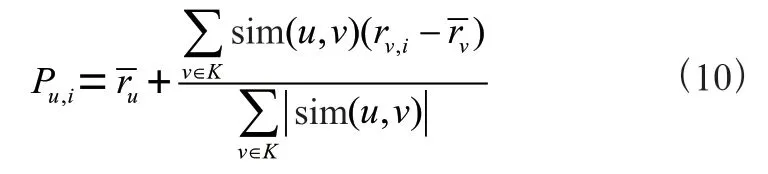
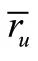
（2）项目本身质量。影响实验结果的另一个原因是，在上述计算相似度的过程中，仅仅从已有评分判断用户兴趣偏好，而没有考虑到项目本身的质量也会影响用户评分。因此，在相似度计算时应该对用户评分数据的离散性进行加权，纠正项目质量所带来的误差。在统计学中，通常用极差、四分位差、方差、标准差和变异系数等描述一组数据离散程度。这里用项目评分的方差来衡量评分数据的离散性，方差计算公式如式（11），它使用平方的方式求和后取平均值，能够避免正负数的相互抵消。方差越小说明数据对平均值的偏离越小，评分数据则越稳定。为了更精确地计算项目之间的相似度，引入离散系数，项目的离散系数的计算公式如式（12）。

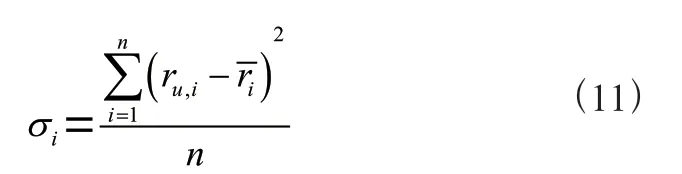
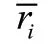
将离散系数（式（12））与Pearson相关系数计算公式相结合得到相似度计算公式（13），该公式在Pearson相关系数的基础上，融入对项目质量的加权，利用该公式计算项目之间的相似度会更加精准，因而理论上能有效提高推荐质量，这仍需要后续研究进行验证。

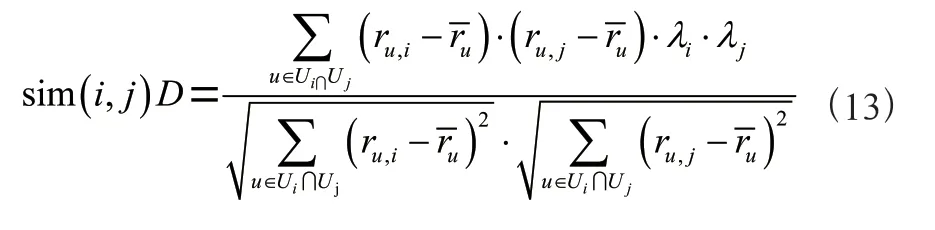
3 结 论

本文围绕协同过滤推荐算法开展研究，借助电商平台数据集，通过实验对比了四种不同相似性度量方法对推荐结果的影响。从实验结果看，改进的相似度计算方法在准确率、召回率、均方根误差和平均绝对误差这四个方面有更好的表现，此外，修正的余弦相似度与Pearson相关系数计算方法的推荐效果明显比余弦相似度计算方法的推荐效果好。本实验因没有考虑数据稀疏性和项目本身质量的问题影响了推荐的准确性，故在此基础上分析了实验改进的方法和思路，作为后续研究的方向。