基于PCB方案的多极磁铁谐波测量系统设计与实现

韩文杰 陈 庚 秦 斌 刘 旭 李纯漪

基于PCB方案的多极磁铁谐波测量系统设计与实现

韩文杰 陈 庚 秦 斌 刘 旭 李纯漪

（强电磁工程与新技术国家重点实验室（华中科技大学电气与电子工程学院） 武汉 430074）

磁场测量技术是粒子加速器的核心技术之一，准确可靠的磁场测量数据可为磁铁准直安装、调试运行提供重要依据，确保束流品质。多极磁铁磁场谐波品质是影响束流输运的关键技术指标。针对传统绕制线圈几何尺寸及定位精度不高、测量重复性和稳定性难以控制等问题，该文提出一种基于印制电路板（PCB）技术制作一致性较高的谐波线圈方案，分别从谐波线圈测磁理论、PCB设计、机械结构设计等角度开展设计优化与系统实现，并搭建多极磁铁谐波磁场测量系统，进行绕制线圈与PCB线圈的实验测量比对。结果表明：与绕制谐波线圈相比，基于PCB方案的谐波线圈可实现更高的反抵率以及更为稳定、精确的磁场测量结果，验证了PCB谐波线圈在多极磁铁谐波磁场测量中的显著优势，可为国内PCB谐波线圈发展与工程应用提供参考。

谐波线圈 印制电路板技术 多极磁铁 粒子加速器

0 引言

粒子加速器是研究核物理、高能物理的重要手段，并广泛应用于肿瘤诊断与治疗、同位素生产、无损检测、材料辐照改性及空间辐射模拟等领域。磁场测量技术是粒子加速器的关键技术之一，准确可靠的磁场测量数据在加速器生命周期的各个阶段均具有重要意义，是加速器束流动力学模拟、磁铁准直安装以及束流调试的根本依据[1]。近年来，随着高能加速器的不断发展以及加速器装置在医学中的应用（如：质子/重离子治疗等），对多极磁铁磁场测量精度及测量效率要求也不断提高；另一方面，在大型粒子加速器装置中，通常包含大量的各类磁铁部件，磁场测量工作任务繁重，持续时间较长，这也要求磁场测量系统具有较高的长期稳定性。寻找一种简单、快速、精准、稳定的磁场测量手段可以显著地提高磁场测量效率，缩短加速器装置建造周期。

四极、六极等多极磁铁广泛应用于粒子加速器及其束流传输系统，实现束流的聚散焦、色差校正等功能，其磁场的高次（非理想）谐波相对基波比例，通常需控制在5×10-4范围以内。目前，加速器磁铁的磁场测量主要采用霍尔点测和感应线圈方法。霍尔探头广泛地用于磁场的点测[2]，其尺寸小、空间分辨率高、磁场测量范围也相对较宽，但对于环境温度较为敏感，需进行温度补偿及定期校准。相比而言，综合考虑测量精度、测量效率及测量稳定性等方面，感应线圈法是最合适的谐波磁场测量方法[3-4]，其基本原理是法拉第电磁感应定律，利用感应线圈中磁通量的变化来测量磁场，因而对线圈的几何尺寸和位置精度要求较高。传统感应线圈采用机器或手工绕制，难以保证线包的位置精度，同时，线圈的尺寸效应使得线圈常数和几何因子难以精确确定，为实现高精度的磁场测量，需要使用标准磁铁或其他高精度设备对感应线圈进行校准[5-6]。

基于印制电路板（Printed Circuit Board, PCB）技术的感应线圈一直被广泛地应用于电力系统谐波检测（PCB罗氏线圈）[7]、脉冲电流测量（PCB空心线圈）[8]以及无线传能系统[9]等领域。近年来，国外一些实验室开始将PCB技术应用于加速器磁铁测量领域[10-12]，以期望解决手绕线圈精度不高、线圈间面积差异较大的问题。相较于传统的绕制感应线圈，PCB感应线圈的优势主要体现在[13-14]五方面：

1）PCB线圈的布线精度可以达到1～2μm，且可以进行精确测量。

2）PCB线圈形状可任意定制，布线路径能够沿着理想粒子轨迹来测量积分磁场。

3）PCB线圈重复性好，可批量生产。

4）PCB线圈长期稳定性好，且对温度变化不敏感，能够减少线圈校准次数，并缩短整个磁场测量周期。

5）PCB线圈可用于测量孔径较小磁铁的磁场品质。

基于以上特点，PCB谐波线圈在多极磁铁磁场测量中已展现出突出优势。2011年，O. Dunkel等研制出“Mono-Bloc”型PCB谐波线圈，将沿切向分布的三个线圈直接印制在PCB板不同层内。采用这种方法可以减小切向线圈的装配与定位误差及线圈尺寸误差[15]。P. Arpaia等研制出一款超薄PCB线圈。感应线圈采用双层结构，厚度仅有1.38 mm，并用人造蓝宝石作为线圈支撑结构材料[16]，经过校准后，线圈高阶分量重复测量误差小于0.2×10-4。2021年，欧洲核子研究组织（Organization Européennepour la Recherche Nucléaire, CERN）磁体组对FCC-ee项目中的斜螺线管超导四极磁体进行小电流（5A）测量，通过分段的旋转线圈测试了超导四极磁体的磁场品质，同时采用正反两个方向旋转的方式来减小地磁场以及环境噪声造成的影响，展现了PCB谐波线圈在高精度磁场测量中的显著优势。

在国内加速器装置中，磁场测量主要采用传统的绕制感应线圈（平移线圈和谐波线圈）、霍尔探头、振荡线等方案，获得了较高的测量精度，但未见采用PCB谐波线圈方案的公开文献。中国散裂中子源（China Spallation Neutron Source, CSNS）在交流磁铁和部分直流磁铁测量中分别采用绕制的径向谐波线圈和小型flip线圈来完成高阶谐波分量和局部磁场强度的测量[17-18]，解决了批量磁铁之间的不同中心高度、质量、有效长度、磁场强度的兼容性难题。

本文主要介绍了一种基于PCB方案的谐波线圈设计与实验研究，在谐波磁场测量理论基础上，从线圈反抵方式、PCB设计以及机械结构设计等方面介绍了谐波线圈的设计，分析了PCB线圈工艺控制和测试方法，最后对比了PCB线圈和绕制线圈的测试结果。

1 磁场测量理论

加速器磁铁的磁场品质通常是由中心平面的磁场傅里叶展开来描述，而旋转线圈可以在磁铁孔径内旋转，是测量磁铁高次谐波方便且有效的手段，这一类旋转线圈也被称为“谐波线圈”[19]。在无电流区域，磁场分量如图1所示，磁感应强度角向分量与径向分量可以表示为

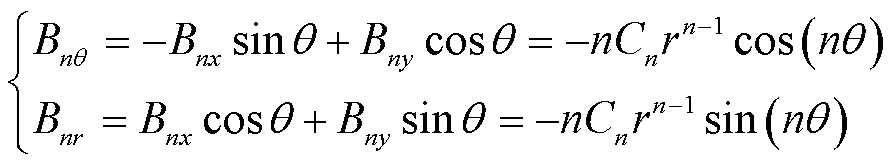
式中，n为谐波次数；为谐波系数。

在无电流源的二维区域，磁场的角向分量与径向分量可以表示为

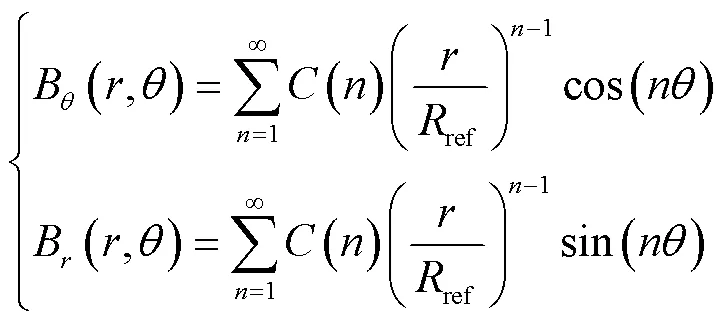
式中，()为磁场谐波系数；ref为任意的参考半径。在笛卡尔坐标系中（ieiθ），磁感应强度()可表示为

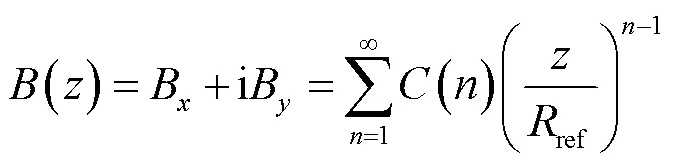
当线圈在磁场中旋转时，会在感应线圈中产生电压信号，该信号直接反映了磁场强度，这也是谐波线圈测量磁场的基础。

根据线圈位置的不同，多极磁铁的磁场测量可以分为切向线圈和径向线圈，如图2所示。切向线圈方法是由F. E. Mills等在1973年提出，即采用静态线圈阵列来测量任意多极磁场谐波分量，线圈的数量决定了能够测量的磁场谐波阶数[20]。线圈表面与磁场分量垂直，测量磁场径向分量并进行频谱分析得到各高阶分量。测量过程中线圈保持静止，可以进行AC模式下的谐波测量。但切向线圈阵列对各线圈的一致性要求较高，采用手工/机器绕制很难实现，因而PCB技术最先引入到切向线圈的制作中。早在2003年，美国布鲁克海文国家实验室（Brookhaven National Laboratory, BNL）的P. Wanderer等制作16路切向PCB线圈[21]，完成德国亥姆霍兹重离子研究中心（GSI）交流四极磁铁谐波分量的在线测量，但刚性线圈不能使得磁场径向分量与线圈表面处处垂直，会产生一定的测量误差。径向线圈则沿磁铁半径方向排布，对磁场角向分量进行测量和分析，在加速器磁铁谐波测量中应用更广。

图2 线圈截面示意图

一般来说，径向线圈对磁场的角向分量较为敏感，任意角度方向上线圈磁通量可以表示为

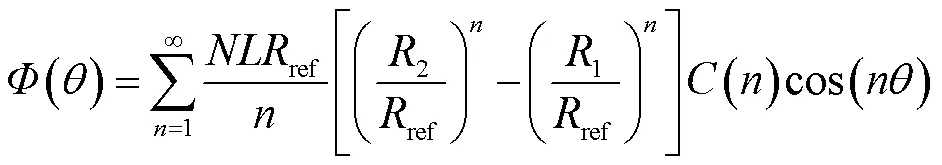
式中，为线圈匝数；为线圈沿磁轴的有效长度；1与2为线圈两侧与旋转轴的距离，如图2a所示，其符号与位置相关，若二者位于旋转轴同侧，则1为正；若二者位于旋转轴不同侧，则1符号为负。假定线圈以角速度旋转，是=0时刻谐波线圈的角位置，则径向线圈中的感应电压信号可以表示为

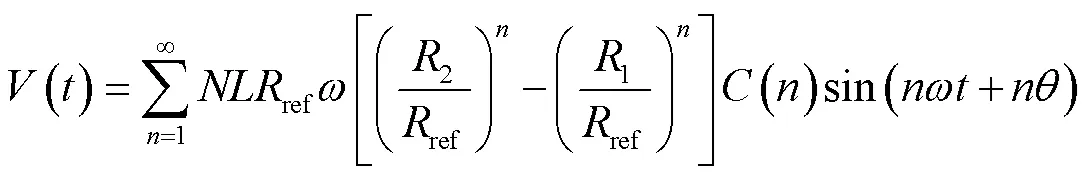
感应电压幅值与线圈转动角速度相关，实际测磁过程中线圈角速度并不完全保持恒定，线圈内感应电压信号会发生畸变，由此感应电压直接分析会得到杂散磁场谐波信号。若想利用感应电压分析磁场谐波，必须严格控制角速度恒定且需要对速度波动进行矫正。为了获取准确的磁场谐波并简化测量过程，可以将线圈感应电压信号积分，即

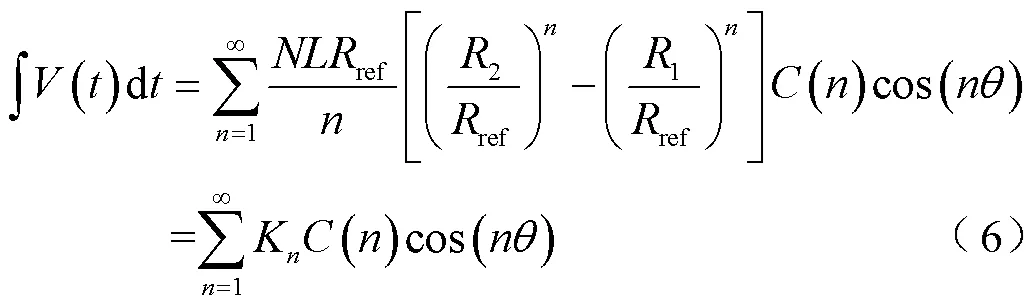
式中，K为线圈系数。当线圈在一个理想多极磁场中旋转，获取的积分感应电压信号是一个周期信号，磁通函数可以表示为

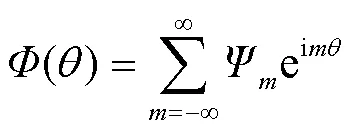
式中，Ψ为傅里叶系数，可以表示为

由式（8）可以求得

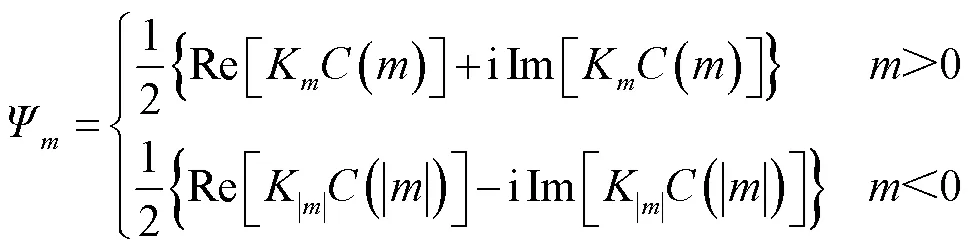
一般情况下，可以用正频率半轴（＞0）来描述完整信号状态，即

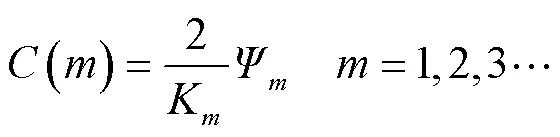
通过积分感应电压信号，可以得到磁场谐波系数()，进一步可推导出被测磁铁积分场、磁场谐波、旋转中心和磁中心偏差等核心参数。

2 PCB线圈设计

华中科技大学正在建设一套基于超导回旋加速器的质子放疗装置，其束流输运与能量选择系统包含多台二极磁铁和四极磁铁。二极磁铁主要用于实现对质子束的偏转，而四极磁铁用于实现对质子束的聚散焦。质子治疗装置中四极磁铁参数见表1，其中四极磁铁最大磁场梯度为19T/m，孔径为40mm。为实现对四极磁铁磁场品质的评估，华中科技大学前期与中国科学院近代物理研究所共同研发了一套基于绕制线圈的旋测装置，但是绕制线圈接线复杂，在绕制过程中需要复杂的缠绕技术和焊接技术。同时，绕制线圈精度不高，难以实现较高的反抵率和测量重复性，造成多台磁体测试过程中可能需要反复校准线圈，也难以实现长期、稳定测量。而本文提出的PCB谐波线圈方案的参数设计主要针对华中科技大学质子治疗装置的四极磁铁开展。

表1 四极磁铁设计参数

Tab.1 Specifications of quadrupole magnets

2.1 线圈反抵设计

基于谐波线圈的测量原理，感应线圈在磁场中的感应电压积分经过傅里叶分析后可得到各极磁场分量，谐波线圈可以快速准确地测量多极磁铁的主极分量和高阶分量。然而，由磁铁加工及装配误差造成的高阶分量非常小，往往需要引入反抵线圈将主极分量消除，大幅度减小由主极分量引入的较大感应电压信号，最终得到被测试磁铁准确的高阶分量。传统的绕制线圈往往采用的是两组线圈，其截面如图3所示，主极磁场分量是在无补偿的情况下使用外部线圈绕组测量，高阶分量是通过采样内外两个线圈信号的差值得到。

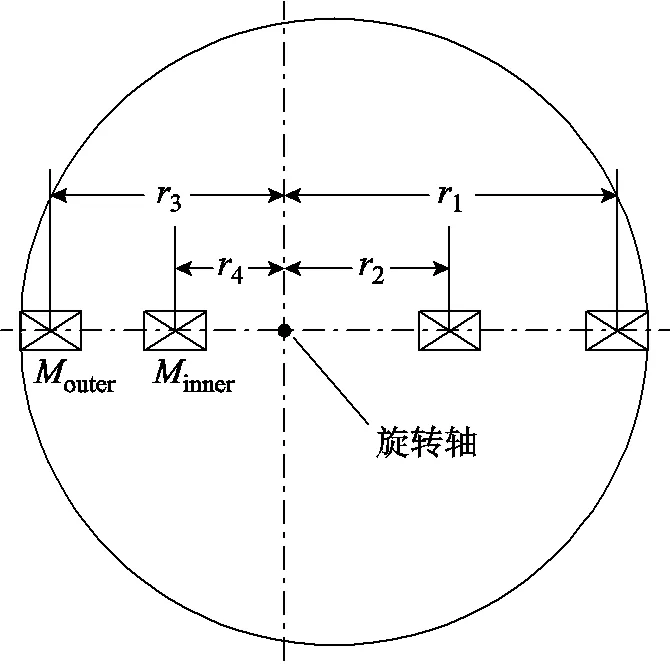
图3 绕制谐波线圈截面示意图

在反抵模式下，外线圈、内线圈以及反抵线圈的积分电信号可以分别表示为

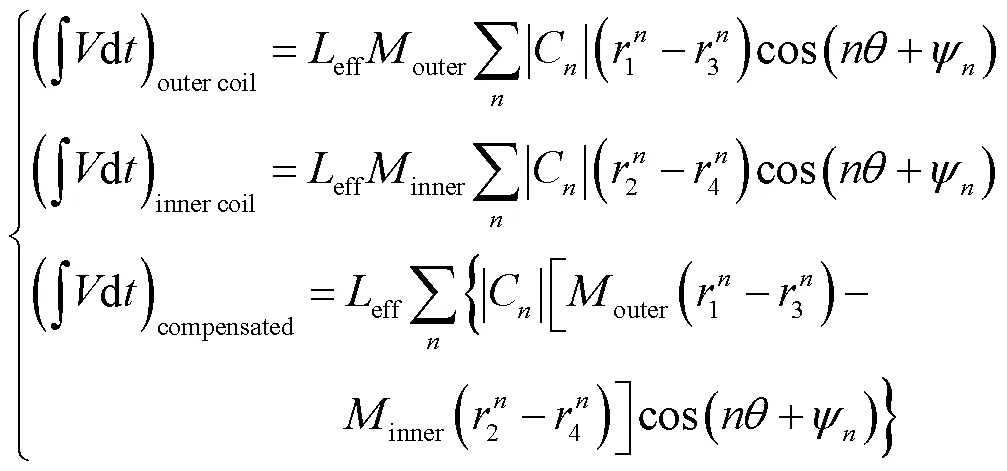
式中，eff为线圈的有效长度；outer为外线圈的线圈匝数；inner为内线圈的匝数。假设1=|3/1|，2=|4/2|，=2/1，=inner/outer，式（11）可以表示为

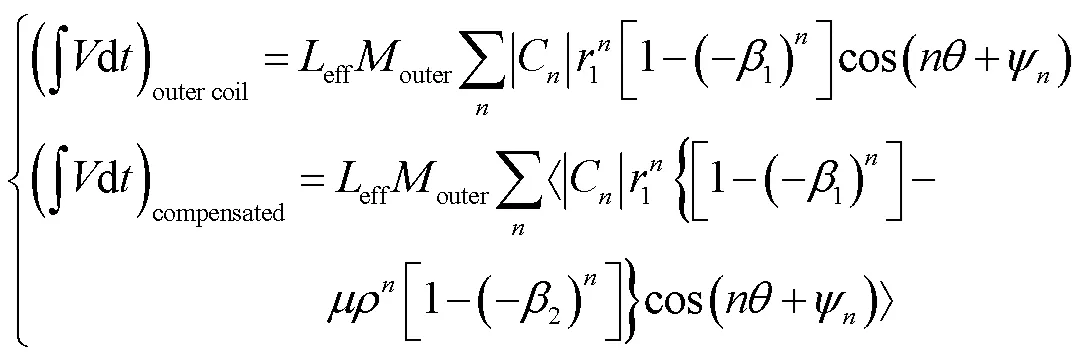
原信号和反抵信号的补偿系数可以表示为

对于四极磁铁的磁场测量，谐波线圈在设计过程中需要将反抵线圈中的四极场（=2）和二极场（=1）的补偿系数设为零，即

采用PCB线圈也可以采用与传统绕制线圈一样的反抵方式，但是线圈制作复杂，且对每个线圈定位精度较高。为了简化PCB线圈设计，拟采用多个相同的线圈平行等间距放置，其截面示意如图4所示。对于一个宽度为的线圈，其二极磁场、四极磁场和六极磁场的线圈系数分别为

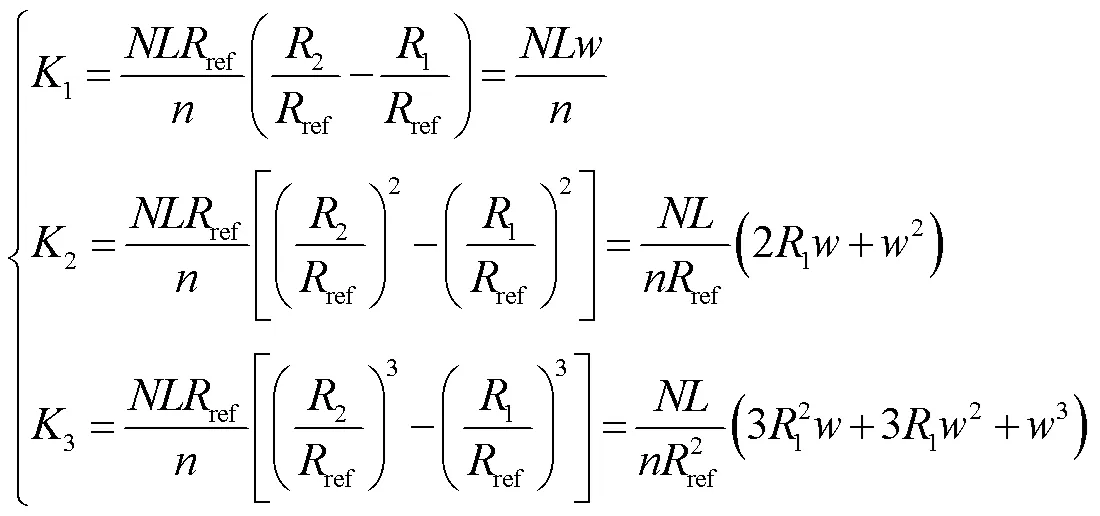
对于单个线圈，其线圈系数只与线圈所在位置和线圈宽度相关，如图4所示，各线圈长度、匝数以及宽度相同，采用两个相同的线圈（线圈A、线圈B），可以实现二极分量反抵；若采用两组相同的线圈（第一组线圈、第二组线圈），可以实现四极分量反抵；若采用两层相同线圈（第一层、第二层），可以实现六极分量反抵。通过这种方式，可以实现二极磁场、四极磁场、六级磁场甚至更高阶磁铁的磁场分量。为了简化PCB线圈设计与制造工艺，采用多个相同线圈等间距放置的设计方案。

2.2 PCB线圈设计

一般而言，PCB线圈有两种制板工艺：双层PCB工艺和单层PCB工艺，如图5所示。双层PCB两端采用对称铜线圈结构，层间由预浸层（Pre-preg）绝缘并将上下层固定在一起。单层PCB仅在一侧布置铜线圈，可用作改善铜轨道对齐并降低PCB总厚度，在这种方案下，绝缘层交替使用预浸料和FR4。单PCB层通常不是直接制成，需要通过蚀刻从一侧去除铜来获得，同时难以保证多层制作时线圈的中心对称，从而造成中心偏移。为了确保线圈处于旋转轴中心，本文采用双层PCB制板方案。

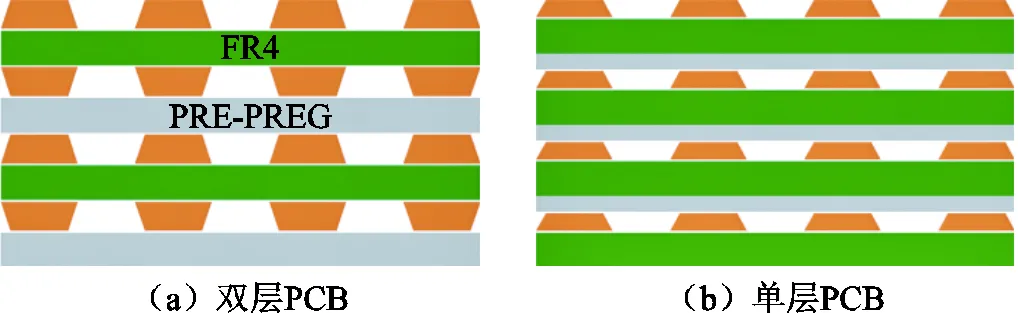
图5 双层PCB与单层PCB示意图

PCB谐波线圈采用径向五线圈结构，五个线圈宽度与匝数相同。为了方便线圈后续安装与定位，线圈中间预留五个定位孔，同时在两侧各预留五个固定孔位。PCB线圈结构如图6所示。理论上，PCB线圈的铜轨迹宽度可以限制在50μm，甚至更小，但是较细的铜轨迹会增加线圈的制造难度，同时也会降低PCB成品率和线圈可靠性。为确保加工精度，需要在一定程度上增加铜轨迹宽度，并采用增加层数的方式来降低线圈宽度的影响。综合考虑制板工艺以及信号大小等因素，PCB印刷铜轨迹线宽=150μm，轨迹间距=150μm，采用6层板单层布线，单个线圈匝数为60匝，PCB线圈布局如图7所示。

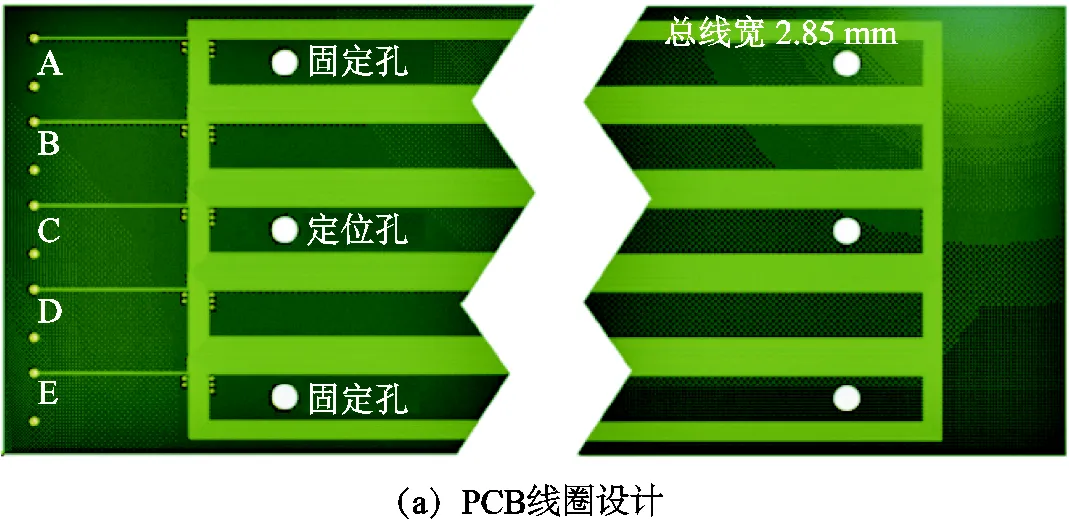
图7 PCB线圈布局

2.3 机械结构设计

为提高线圈主轴强度和降低整体重量，采用双层固定夹板式结构，两个夹板使用加强筋支撑，利用两个T型夹板固定PCB线圈，并在T型夹板上增加固定孔与定位孔。两个夹板与PCB装配作为十字主轴，主动轴、从动轴与线圈十字轴采用子母口连接。线圈主轴如图8所示。图9为装配后的PCB线圈实物图。

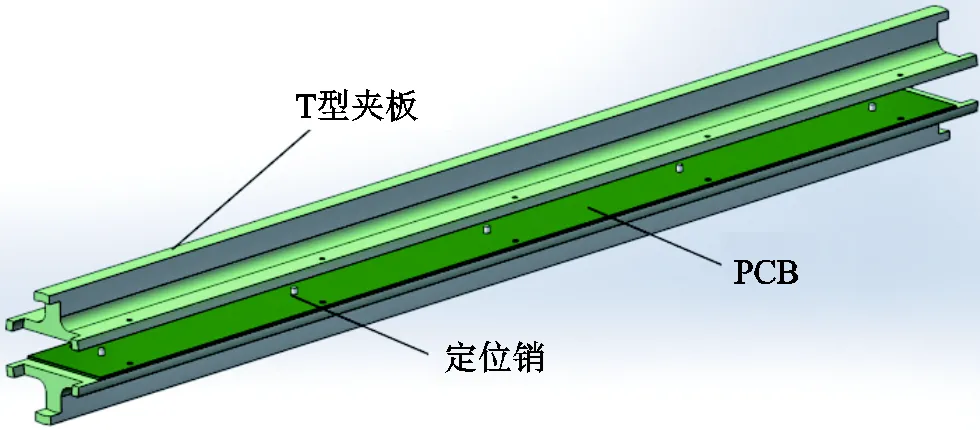
图8 线圈主轴示意图

图9 PCB线圈实物图

2.4 线圈工艺控制与检测

PCB线圈的检测一般需要通过截取部分布线路径片段来衡量线圈制作工艺，PCB线圈设计之初，在线圈周围设置用于控制制作工艺的铜轨迹。在线圈出厂之前，通过百倍显微镜测量线宽、线间距以及孔径偏差，同时利用金相切片测量不同层的线圈对齐情况以及线圈位置偏差。PCB线圈切面如图10所示。经过检测，线圈层间误差小于10μm，各项指标测试结果见表2，均符合要求。

图10 PCB线圈切面

表2 PCB线圈参数设计值与实测值

Tab.2 The design parameters and measurement results of the PCB coil

3 可靠性验证

在完成线圈加工后，需要测量线圈的稳定性、可靠性以及测量重复性。基于PCB线圈的谐波磁场测量系统如图11所示，主要包括：旋转电机及其控制器、编码器、谐波线圈、积分器、磁铁电源、直流电流传感器（Direct Current Current Transformer, DCCT）以及数据采样系统。被测试磁铁置于磁铁支撑上，利用该平台可以调节磁铁位置；谐波线圈放置于大理石基座V型金属支撑件上固定。当计算机通过命令控制磁铁电源输出电流时，在被测试磁铁中产生相应的磁场，而后由旋转电机带动谐波线圈匀速旋转，从而在线圈中产生电压信号；编码器用于确定谐波线圈位置并输出触发脉冲，从而控制积分器采集；积分器FDI2056一路采样谐波线圈的主线圈信号，另一路采样反抵线圈的反抵信号，最后由上位机进行傅里叶分析，确定谐波分量。至于励磁电流则是由DCCT转化成等比例的电压信号，而后由数字采集卡PCIe4065采样，最后传输至计算机。搭建完成的磁场测量系统如图12所示。

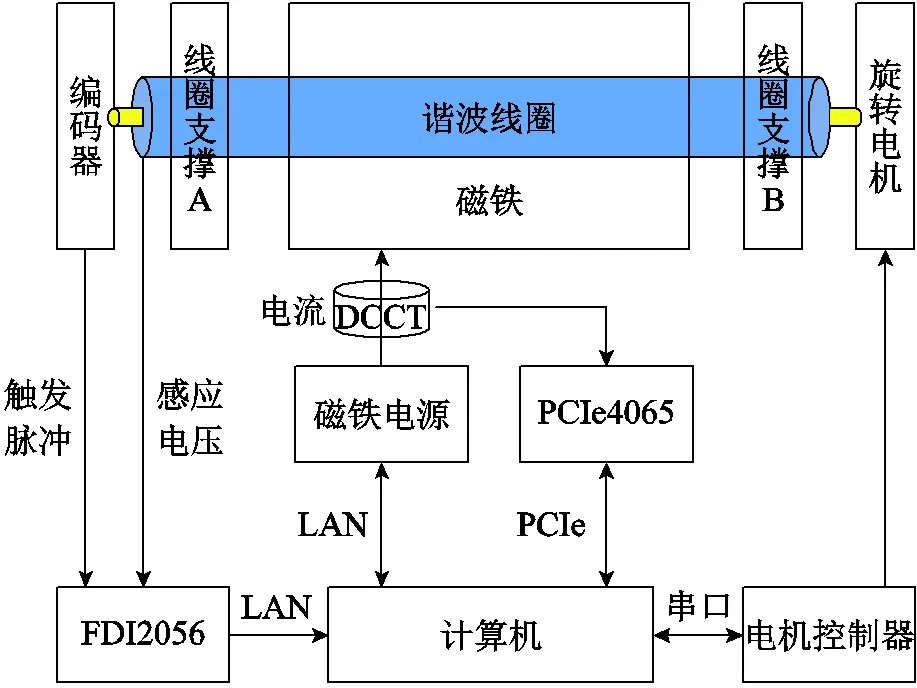
图11 谐波线圈磁场测量系统原理

图12 基于PCB谐波线圈的磁场测量现场

3.1 短期重复性

在短时间内，同一磁铁往往需要经过多次测试，而短期重复性是衡量线圈是否满足设计要求的重要指标。图13展示了励磁电流为100A时，四极磁铁样机30次重复测量结果，柱状图上短线为30次重复测量的标准差。在=20及以下的高阶谐波分量上，绕制线圈测量标准差为0.7units（1unit表示0.01%），PCB线圈的测量标准差为0.08units。PCB线圈的测量重复性优于绕制线圈一个数量级，测量的高阶谐波波动小，短期测量结果重复性好。

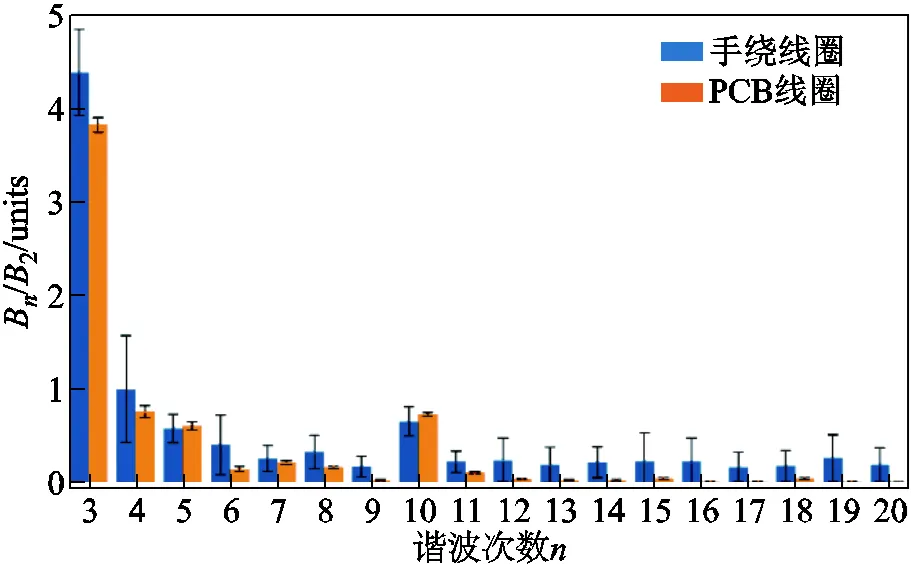
图13 短期稳定性测量结果

3.2 长期稳定性

长期稳定性主要衡量的是线圈在长时间放置或测试过程中线圈多次测量的重复性。在保持测量条件不变前提下，分别于2021年10月、2021年12月以及2022年3月各选一周对同一台四极磁铁样机进行多次测量，观察PCB线圈的测量重复性。图14展示了励磁电流为100A时，四极磁铁样机三个月中的30次重复测量结果。在=20及以下的高阶磁场测量上，测量标准差小于0.1units。由一周内的短期测量结果以及半年内的长期测量结果可知PCB线圈的测量长期稳定性远优于绕制线圈。

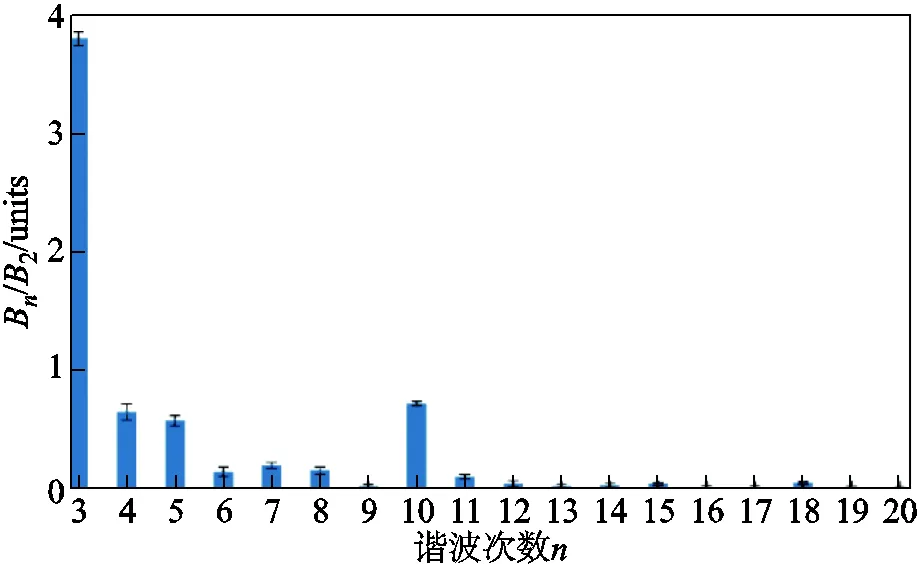
图14 长期稳定性测量结果

3.3 线圈反抵率

反抵率是谐波线圈的一个重要指标，高反抵率可以大幅度降低反抵线圈中的主极分量，减小主极分量对测量精度的影响。反抵率可以由主线圈信号中主极分量幅值除以反抵信号中主极分量幅值得到。谐波线圈的反抵率体现了线圈制作精度，反抵率越高，线圈制作精度越高，一般要求谐波线圈的反抵率大于100。励磁电流为100A时，绕制线圈和PCB线圈主信号与反抵信号电压积分波形如图15所示。绕制线圈和PCB线圈的反抵率分别为104和1 400。相较于绕制线圈，PCB线圈的反抵率提升了一个数量级，高阶谐波受到主极信号干扰小，谐波分量的测量结果具有更好的重复性。

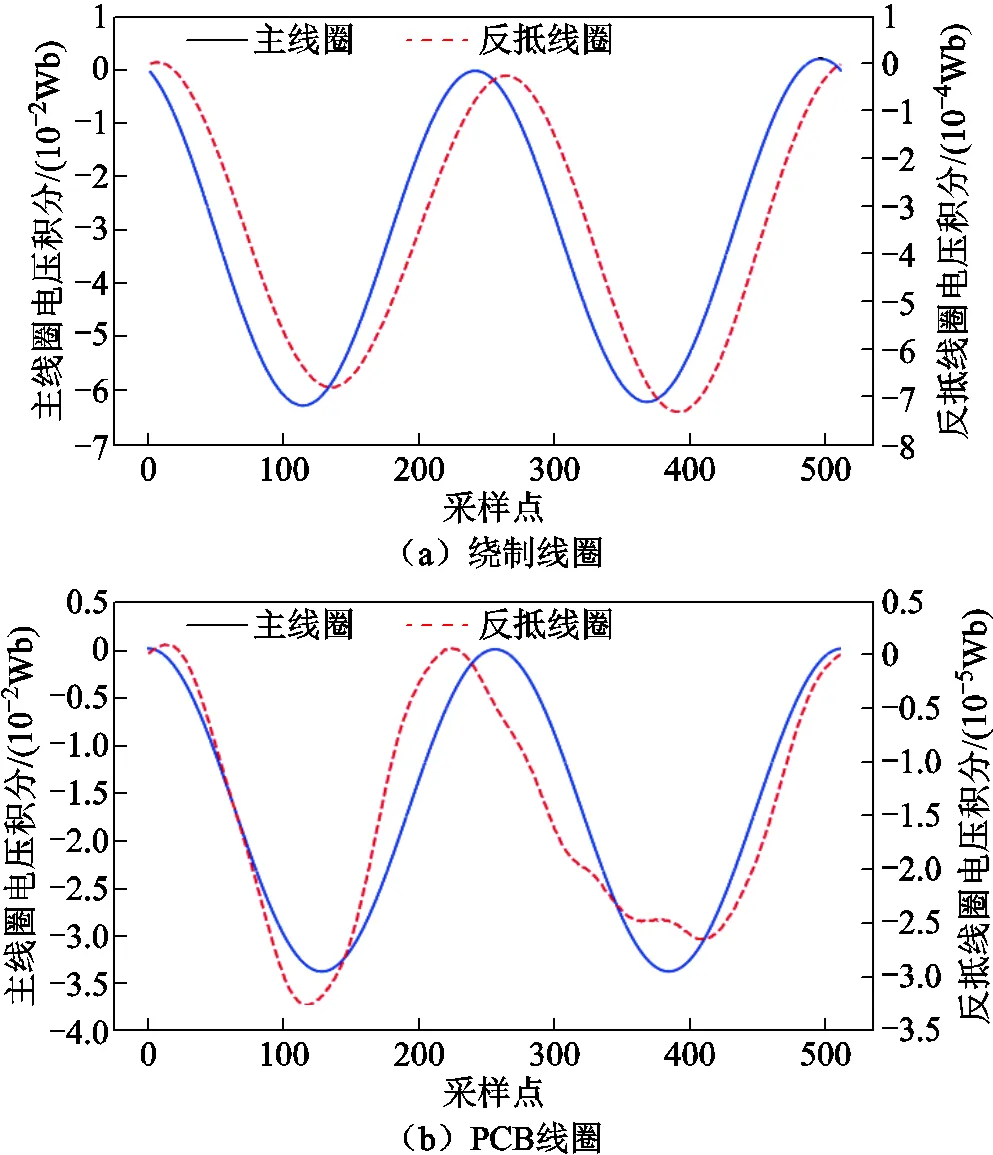
图15 绕制线圈与PCB线圈主信号及反抵信号图

4 结论

本文针对传统绕制线圈精度不高、测量一致性差等问题，采用PCB技术制作一致性较高的线圈阵列，并开展了谐波线圈磁场测量理论研究；基于PCB谐波线圈的方案特性，提出了采用多个相同线圈等间距放置的反抵方案，并从线圈参数设计、机械结构设计以及工艺控制等方面进行探讨。搭建了一套基于PCB感应线圈的谐波测量系统，并开展了线圈的可靠性验证，从长期稳定度、短期稳定度、线圈反抵率等方面与绕制线圈进行比对。测试结果表明，基于PCB技术制作的谐波线圈精度高、稳定性好，可以实现更高的反抵率以及更为精确、稳定的谐波磁场测量结果，验证了PCB技术在谐波测量系统中的显著优势，为PCB谐波线圈在国内加速器磁铁中的发展与应用提供了基础。

[1] 何源. CSR磁场测量系统的建立及应用[D]. 兰州: 中国科学院近代物理研究所, 2003.

[2] Sanfilippo S. Hall probes: physics and application to magnetometry[R]. Bruges: CERN Accelerator School, 2009.

[3] Walckiers L. Magnetic measurement with coils and wires[R]. Bruges: CERN Accelerator School, 2009.

[4] Buzio M. Fabrication and calibration of search coils[R]. Bruges: CERN Accelerator School, 2009.

[5] Arpaia P, Buzio M, Golluccio G, et al. In-situ calibration of rotating coil magnetic measurement systems a case study on Linac4 magnets at CERN[C]// 17th Symposium IMEKO TC4, Kosice, Slovakia, 2010: 200-204.

[6] Arpaia P, Buzio M, Köster O, et al. Rotating-coil calibration in a reference quadrupole, considering roll-angle misalignment and higher-order harmonics[J]. Measurement, 2016, 87: 74-82.

[7] 陶涛, 赵治华, 潘启军, 等. 一种抗强干扰型双面对称布线PCB罗氏线圈[J]. 电工技术学报, 2011, 26(9): 130-137.

Tao Tao, Zhao Zhihua, Pan Qijun, et al. Design of PCB Rogowski coil and analysis of anti-interference[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 130-137.

[8] 韩小涛, 黄澜涛, 孙文文, 等. 基于PCB空心线圈和数字积分器的脉冲强磁场装置放电电流测量[J]. 电工技术学报, 2012, 27(12): 13-19.

Han Xiaotao, Huang Lantao, Sun Wenwen, et al. Discharge current measurement of pulsed high magnetic field facility based on PCB air-core coil and digital integrator[J]. Transactions of China Electrotechnical Society, 2012, 27(12): 13-19.

[9] 陈新, 张桂香. 基于PCB线圈的无线传输系统功率与效率分析(英文)[J]. 电工技术学报, 2015(增刊1): 159-167.

Chen Xin, Zhang Guixiang. Power and efficiency analysis of a PCB based wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2015(S1): 159-167.

[10] Borisov V, Donyagin A, Golubitsky O, et al. Magnetic measurement system for the NICA booster magnets[C]// Proceedings of the 5th International Particle Accelerator Conference, Dresden, Germany, 2014: 2696-2699.

[11] Shandov M, Borisov V, Bychkov A, et al. Magnetic measurement system for the NICA collider dual dipoles[C]// Proceedings of the 25th Russian Particle Accelerator Conference, St.Petersburg, Russia, 2016: 547-549.

[12] Shandov M M, Borisov V V, Bychkov A V, et al. First serial magnetic measurements of the NICA collider twin-Aperture dipoles[C]// Proceedings of the 9th International Particle Accelerator Conference, Vancouver, Canada, 2018: 3645-3648.

[13] Golluccio G, Beaumont A, Buzio M, et al. PCB coil array for measuring curved accelerator dipoles: two case studies on the MedAustron accelerator[C]// Proceedings of 20th IMEKO TC4 International Symposium and 18th International Workshop on ADC Modelling and Testing, Benevento, Italy, 2014: 816-821.

[14] 李冠群, 韩文杰, 秦斌, 等. 用于质子治疗的Kicker磁铁动态磁场测量[J]. 核技术, 2020, 43(1): 9-14.

Li Guanqun, Han Wenjie, Qin Bin, et al. Dynamic magnetic measurements of a Kicker magnet for a proton therapy facility[J]. Nuclear Techniques, 2020, 43(1): 9-14.

[15] Dunkel O. A rotating coil array in “mono-bloc” printed circuit technology for small scale harmonic measurements[R]. Terrassa: IMMW 17-International Magnetic Measurement Workshop, 2011.

[16] Arpaia P, Buzio M, De Oliveira R, et al. A high-precision miniaturized rotating coil transducer for magnetic measurements[J]. Sensors and Actuators A: Physical, 2018, 274: 37-49.

[17] Zhou J X, Li L, Yin B G, et al. AC magnetic field measurement of CSNS/RCS quadrupole prototype[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2011, 654(1): 72-75.

[18] Zhou Jianxin, Kang Wen, Li Shuai, et al. AC magnetic field measurement using a small flip coil system for rapid cycling AC magnets at the China Spallation Neutron Source (CSNS)[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2018, 880: 80-86.

[19] Tanabe J T. Iron dominated electromagnets: design, fabrication, assembly and measurements[M]. New Jersey: World Scientific, 2005.

[20] Mills F E, Morgan G H. A flux theorem for the design of magnet coil ends[J]. Partilce Accelertors, 1973, 5: 227-235.

[21] Wanderer P, Escallier J, Ganetis G, et al. Development of a precise magnetic field measurement system for fast-changing magnetic fields[J]. IEEE Transactions on Applied Superconductivity, 2004, 14(2): 1826-1829.

Design and Implementation of a Harmonic Coil Field Measurement System for Multipole Magnets Based on PCB Scheme

Han Wenjie Chen Geng Qin Bin Liu Xu Li Chunyi

（State Key Laboratory of Advanced Electromagnetic Engineering and Technology School of Electrical and Electronic Engineering Huazhong University of Science and Technology Wuhan 430074 China）

The magnetic field measurement technology is one of the core technologies of particle accelerators, and the harmonic field quality of multipole magnet is essential to beam transportation. The accurate and reliable magnetic field measurement data can provide important reference for installation, commissioning and operation of magnets for multi-purposes. Compared to relative lower positioning accuracy and repeatability by using traditional hand-wound coils, this paper introduces the design and implementation of a harmonic coil field measurement system based on printed circuit board (PCB) technology. The theory of harmonic field measurement, the design of PCB coil and mechanical support structure are described. A comparative study between the hand-wound coils and PCB coils are performed. The experimental results show that the PCB harmonic coils can achieve more stable and accurate magnetic field measurements with higher bucking rate, for harmonic magnetic fields measurement of multipole magnets. The research findings can provide a good reference for the design and development of harmonics field measurement coils based on PCB technique.

Harmonic coil, printed circuit board technique, multipole magnet, particle accelerators

10.19595/j.cnki.1000-6753.tces.221257

TM936

国家自然科学基金（11975107）和中国博士后科学基金（2021M691132）资助项目。

2022-06-29

2022-07-11

韩文杰 男，1992年生，博士，研究方向加速器磁铁及电源技术。E-mail：hanwenjie@hust.edu.cn

秦 斌 男，1979年生，教授，博士生导师，研究方向为粒子加速器及束流输运。E-mail：bin.qin@mail.hust.edu.cn（通信作者）

（编辑 李冰）