有源中点钳位逆变器的损耗均衡和效率优化策略

万文超 段善旭 余天宝 米慧瑶

有源中点钳位逆变器的损耗均衡和效率优化策略

万文超 段善旭 余天宝 米慧瑶

（强电磁工程与新技术国家重点实验室（华中科技大学电气与电子工程学院） 武汉 430074）

针对有源中点钳位（ANPC）逆变器，基于开关损耗分配的基本原理，建立开关器件的损耗估计模型，提出一种主动调节损耗分布的方法，通过合理分配不同开关器件来承受开关损耗，调节各模态的起始时间和持续时间，尽可能地减小各开关器件之间的损耗差异，并扩展到变功率因数角的场合，该方法实施简单且有效。此外，当桥臂输出电压被钳位到直流中点时，通过对驱动时序的调整和重新构造，使两条零电平回路同时导通（TZCC）进行续流，有效地减小了导通损耗，进一步提升变换器效率。较传统的损耗均衡或效率优化单一目标上，所提方法在损耗均衡的同时又能兼顾其运行效率，充分地发挥出ANPC逆变器的优势。最后，通过仿真和实验验证了所提策略的有效性。

有源中点钳位（ANPC）逆变器 损耗均衡 驱动重构 效率提升

0 引言

中点钳位（Neutral Point Clamped, NPC）型三电平变换器具有器件应力低、功率密度高、电流谐波含量小等优势，被广泛应用于并网光伏、轨道交通牵引变流和数据中心电源等工业应用场合[1-2]。随着输出功率需求的增加，NPC变换器将面临器件损耗分布不均[3]这一主要缺点，导致各功率器件工作结温不一致，降低了系统的可靠性，同时变换器的容量将受到最高结温器件的限制，因此引入有源器件替代钳位二极管[4]，而在有源中点钳位（Active NPC, ANPC）条件下，其具有冗余的驱动分配方式，可用于损耗重新分配和提高系统效率，有利于变换器的大容量高效运行[5-9]。

ANPC逆变单相电路中有6个开关器件，其驱动可分配方式众多，主要分为ANPC-1方法、ANPC-2方法以及两者的组合或变形。ANPC-1采用外管和钳位管高频动作，而内管为工频开关；ANPC-2选择内管高频动作而其他为工频开关。不同的驱动方式造成承担开关损耗的器件不同，因此目前的损耗均衡策略大都基于此[10-15]。

文献[11]引入额外的移相180°载波，将调制波分别与两载波比较得到内外管的驱动信号，此时两管交替开通和关断，使得内外管各承受一次开关损耗。文献[12]通过引入双调制信号，基于硬件PWM配置输出不对称驱动波形，使得开通和关断损耗分离。文献[13-14]通过ANPC-1和ANPC-2交替使用，在它们之间引入过渡模态，在过渡模态下额外的开关管导通和关断并不影响桥臂电压输出状态，因此可具有更多的开关组合，从而实现两种驱动方式的平滑切换。在以上损耗均衡方法中，内外管开关损耗分配固定，无法进行实时调节。针对该问题，文献[15]在单位功率因数下，提出一种基于工频周期调控的变开关损耗分配比例方法，通过在每工频周期内改变ANPC-1与ANPC-2的持续模态时间比，实现对内外管开关损耗的在线调整，但该比例大小如何选取并未给出理论依据。

驱动分配策略除了影响开关损耗分布外，同时也会影响系统效率[16-19]。文献[16]在ANPC-1和ANPC-2两种方法下对变换器效率和器件应力进行了深入研究，结果发现，受寄生电感参数的影响，拥有长换流回路的ANPC-2方法，其器件应力较高且变换器效率略低。文献[17]提出一种改进的驱动策略，所有开关管均为高频动作，等效为ANPC-1与ANPC-2的并联组合，器件电压应力介于两者之间，该方式下将单条零电平钳位回路变成两条钳位回路同时导通（Two Zero-level Clamped loop Conducting, TZCC），因此可进一步降低导通损耗，增加效率。

硬件方法同样被考虑用来提升变换器效率，可在ANPC变换器中引入部分SiC器件[20-23]。按ANPC-1和ANPC-2两种驱动方式分别组成钳位管和外管为SiC（4-SiC HANPC）以及内管为SiC（2-SiC HANPC）的混合ANPC（Hybrid ANPC, HANPC）模块。文献[20]中首次提出2-SiC HANPC混合模块，结合ANPC-2驱动方式，可最大程度地发挥SiC器件的优势，实验表明，在45kHz下最大效率高达99%，输出功率0～4kW，相比于Si器件效率平均高出0.5%～1%。文献[21]基于2-SiC HANPC拓扑，优化设计SiC与Si IGBT器件的额定电流比，效率甚至可以高出采用全SiC器件。文献[22]对2-SiC HANPC和4-SiC HANPC在效率、热特性和功率密度上进行了对比，发现2-SiC HANPC效率与4-SiC HANPC基本一致，但4-SiC HANPC热分布更均匀，因此在采用相同器件等级下，其容量和功率密度更高。此外，还有很多文献针对一些特定应用场合[24-25]，如光伏逆变器等，采用外管为SiC的改进混合模块，其承受全部开关损耗，而内管导通电流大，因而采用Si IGBT。

目前关于ANPC逆变器的热均衡方法，大都采用平衡开关损耗次数，以及针对特定调制比和功率因数角的场合。前者并没有实现真正意义上的总损耗平衡，后者无法扩展到变调制比和功率因数角的情况。在效率优化方面，常被视为独立的目标，同时能够实现热均衡和效率优化的文献较少。

基于以上问题，本文首先针对不同驱动分配方式，得到ANPC逆变器的开关损耗分布规律。其次在考虑变调制比和功率因数角的情况下，对各开关器件的导通损耗和开关损耗进行了理论评估，通过主动调节和分配各模态的起始时间和持续时间，采用不同开关器件来承受开关损耗，使得各开关器件损耗均衡最大化，结果表明该方法实施简单且有效。另外，结合TZCC方法，对驱动时序进行重构，从而有效减小导通损耗，提高变换器效率。最后，通过仿真并在一台ANPC单相逆变器进行系统实验，验证了理论分析的正确性和所提策略的有效性。

1 三种典型的ANPC底层驱动分配方法

开关损耗分布之所以能够被改变是由于各开关器件的驱动时序和分配上存在差异，为防止概念上的混淆，在这里略作说明，通常所说的调制策略如正弦载波调制、空间矢量调制等在这里统称为顶层调制策略，而本节接下来的分析均是针对于正弦载波调制下，在驱动时序和分配上进行的调整，在这里被称为底层驱动分配策略。

将ANPC单相电路分为上桥臂Sa1、Sa2，下桥臂Sa3、Sa4以及钳位桥臂Sap、San。Sa1和Sa4被统称为外管，Sa2和Sa3被统称为内管，Sap和San被称为钳位管。ANPC-1的底层驱动分配方法如图1所示，其在四象限运行下均采用短换流回路。以调制波ra＞0为例，当桥臂电压在P和O状态之间进行切换时，Sa1与Sap高频动作，若a＞0，由软开关条件可知，Sa1承担开关损耗；反之，则由Sap承担开关损耗。ra＜0时可同理分析。

图1 ANPC-1底层驱动分配方法

ANPC-2的底层驱动分配方法如图2所示，其在四象限运行下均采用长换流回路。同样以调制波ra＞0为例，当桥臂电压在P和O状态之间进行切换时，Sa2与Sa3高频动作，若a＞0，则Sa2承担开关损耗；反之，则由Sa3承担开关损耗。ra＜0时可同理分析。

ANPC-TZCC的底层驱动分配方法如图3所示，相比于以上两种驱动策略，采用两条零电平钳位回路同时动作。当调制波ra＞0时，除Sa1与Sap高频动作外，Sa3与Sap同步，若a＞0，则Sa1承担开关损耗；反之，则由Sa3与Sap共同承担开关损耗。ra＜0时可同理分析。

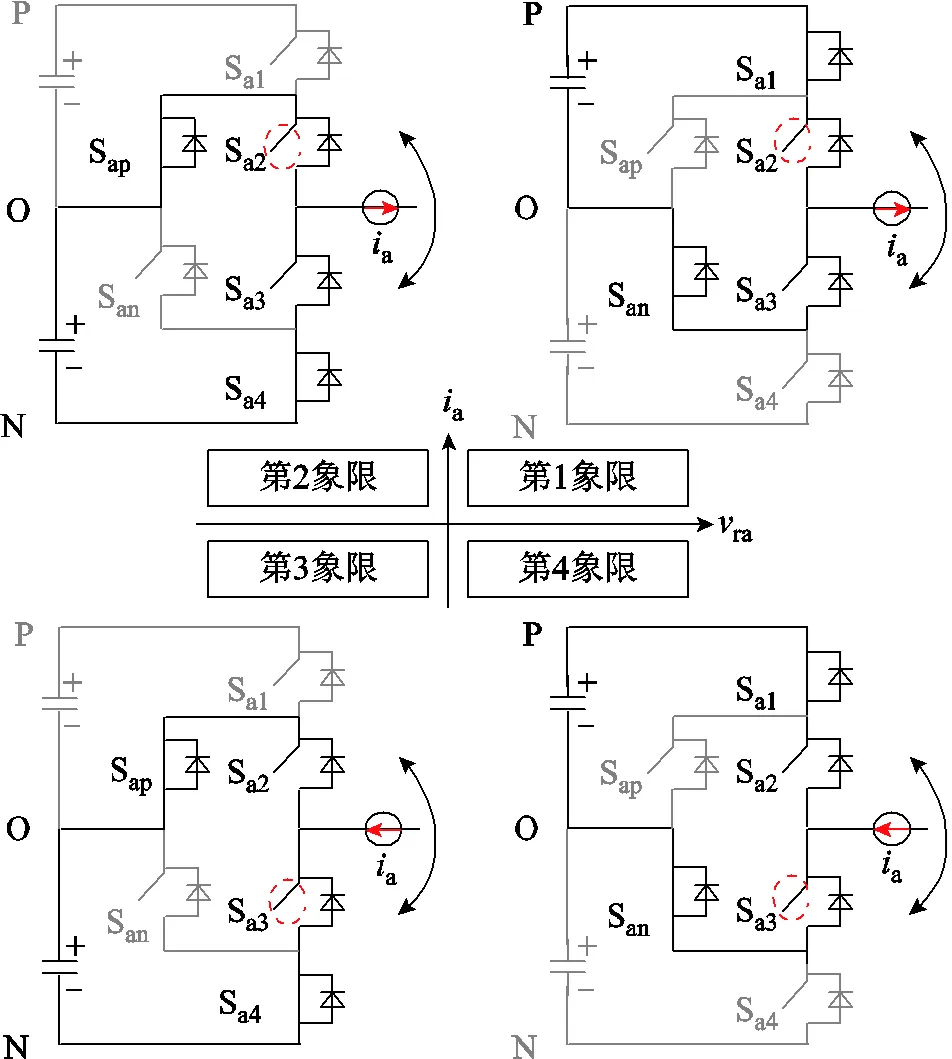
图2 ANPC-2底层驱动分配方法

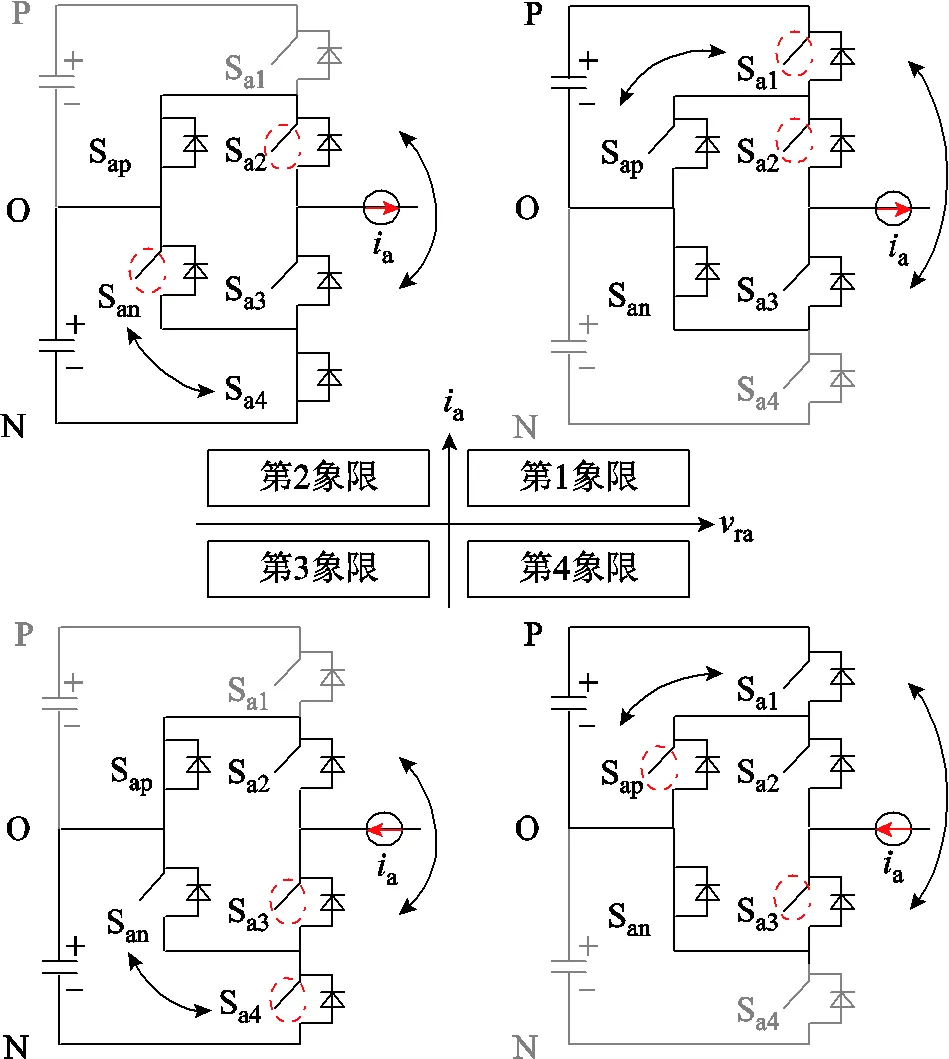
图3 ANPC-TZCC底层驱动分配方法

可以发现，当逆变器处于单位功率因数运行时，以上的任意一种驱动策略下，开关损耗总是全部集中在外管或内管上。通过了解以上不同驱动分配方式下的开关损耗分布规律，可同时采用多种驱动策略，调节其分配时间比例，进而结合不同的开关器件来承担开关损耗，实现开关损耗的主动分配。

2 开关器件损耗评估

开关器件的损耗评估是均衡策略的前提，为实现损耗均衡最大化，以及扩展到调制比和功率因数角变化下的一般应用场合提供了理论依据。

2.1 导通损耗分析

1）开关管电流有效值（忽略死区时间）

开关管电流有效值的表达示为

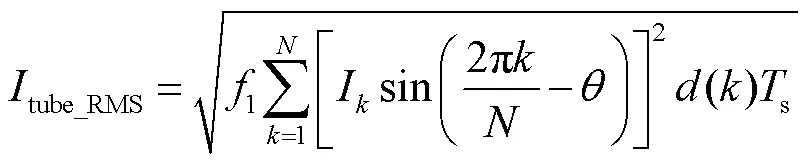
式中，1为基波频率；s为开关周期；为载波比，=s/1()为对应不同开关管下的导通占空比；I为对应各开关管电流幅值；为滞后功率因数角。由式（1）可知，开关管电流有效值与负载大小、功率因数角和底层驱动分配策略有关，另外不同的顶层调制策略和调制比大小，也会影响()的表达式。但无论采用何种调制方法或变换器处于何种工况，其值总是可以通过调制环节计算得出。

2）导通电阻修正

导通电阻与开关管结温有关，两者为二次曲线关系，其具体表达式可通过数据手册拟合得到，则开关管导通损耗为

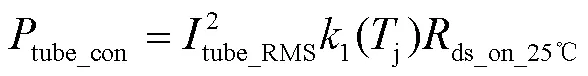
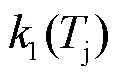
2.2 开关损耗分析

开关损耗与开关速度以及开关时刻的电压电流值有关。开关速度主要取决于驱动电路参数和功率回路的寄生参数，在印制电路板布局时通常就近放置解耦电容，将其功率回路的寄生参数影响减小到最低，因此这里主要根据驱动电阻的变化对开关损耗进行修正；其次，温度的变化同样会导致开关损耗发生改变。则开关管开通和关断一次的能量需要根据数据手册线性修改为

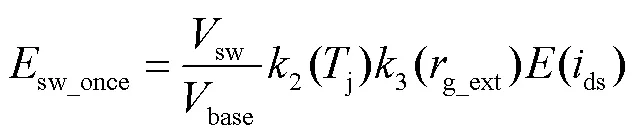
式中，(ds)为在给定开关电压base外部驱动电阻g_ext和结温25℃测试条件下的开关总能量，近似为电流的正比例函数，这种近似在后续仿真和实验中证明是成立的；sw为实际开关电压值；2(j)为开关损耗温度修正系数；3(g_ext)为驱动电阻修正系数。将2和3在测试条件下进行标幺化，最终可表示为

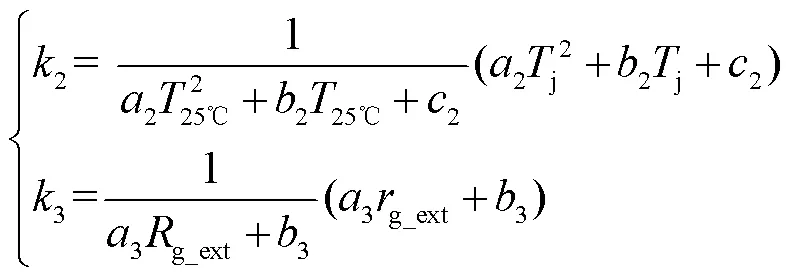
当采用不同开关管进行开关动作时，由于换流回路的差别会导致开关能量有微小差异[26]，在这里可忽略。开关损耗等于单次开关能量在一定时间内的累加，在开关电压保持不变的条件下等效于对开关电流曲线的积分。各开关管的开关损耗积分区间不同，因此开关损耗有所差异。总开关损耗可表示为

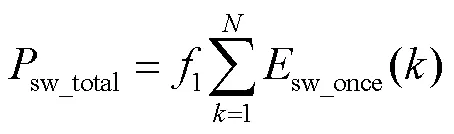
当存在滞后功率因数角时，可得到第1、3象限和第2、4象限内的总开关损耗分别为

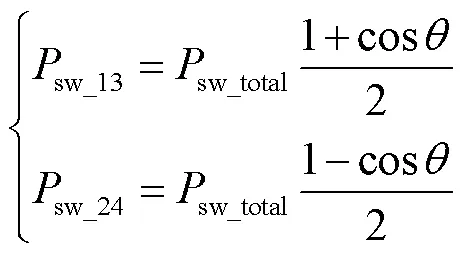
式（6）存在的必要条件是开关管的开关特性基本一致，即相同的(ds)，若是混合模块则只能分别计算。

3 损耗均衡最大化策略

3.1 开关损耗分配原则

1）尽可能采用钳位管承担开关损耗

将第1～4象限分别定义为Q1～Q4。为了满足损耗均衡最大化，损耗均衡最大化下的开关损耗分配原则如图4所示。在Q2和Q4采用ANPC-1策略，可将开关损耗集中于钳位管San与Sap，这样钳位管承担一部分开关损耗，因此加在主桥臂开关管上的总开关损耗减小，总损耗也随之减小。需要说明的是，钳位管能分担的开关损耗随着功率因数角的增加而增加，当=0°时，钳位管无法承担开关损耗。

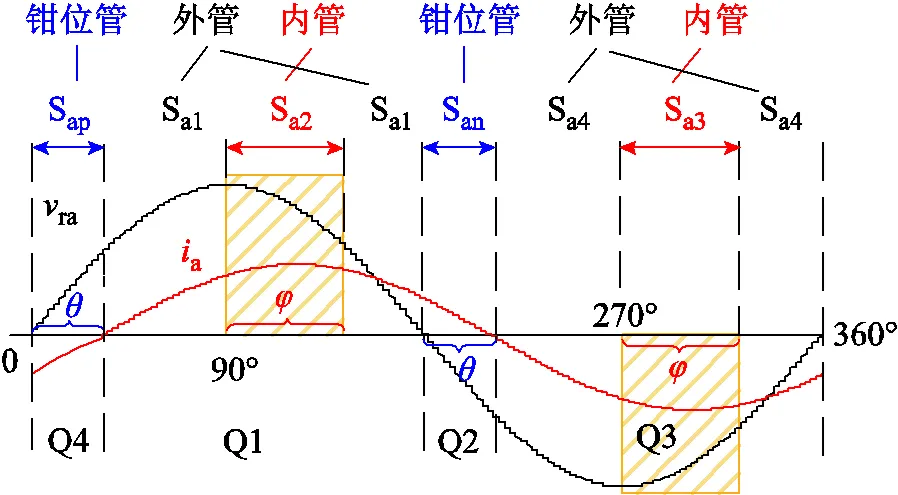
图4 损耗均衡最大化下的开关损耗分配原则

2）调制波峰值处切换驱动分配策略

Q1和Q3为主桥臂开关管承担开关损耗。当处于Q1区时，由Sa1与Sa2共同承担开关损耗，选择在调制波相位90°处切换为ANPC-2方法，采用Sa2承担开关损耗，持续角度为。这里以调制波相位为基准保证了模态切换时的准确性，而不依赖对电流极性的判断；选择在90°处切换保证了功率因数角在大幅变化下切换时刻的存在性，同时又能够最大程度上调节插入模态的开关损耗。同理分析，Sa3与Sa4承担开关损耗的切换时刻选择为调制波相位270°处，持续角度同为。

最终得到工频周期内的驱动策略，损耗均衡策略下的底层驱动分配方法如图5所示，死区时间未在图中标出。

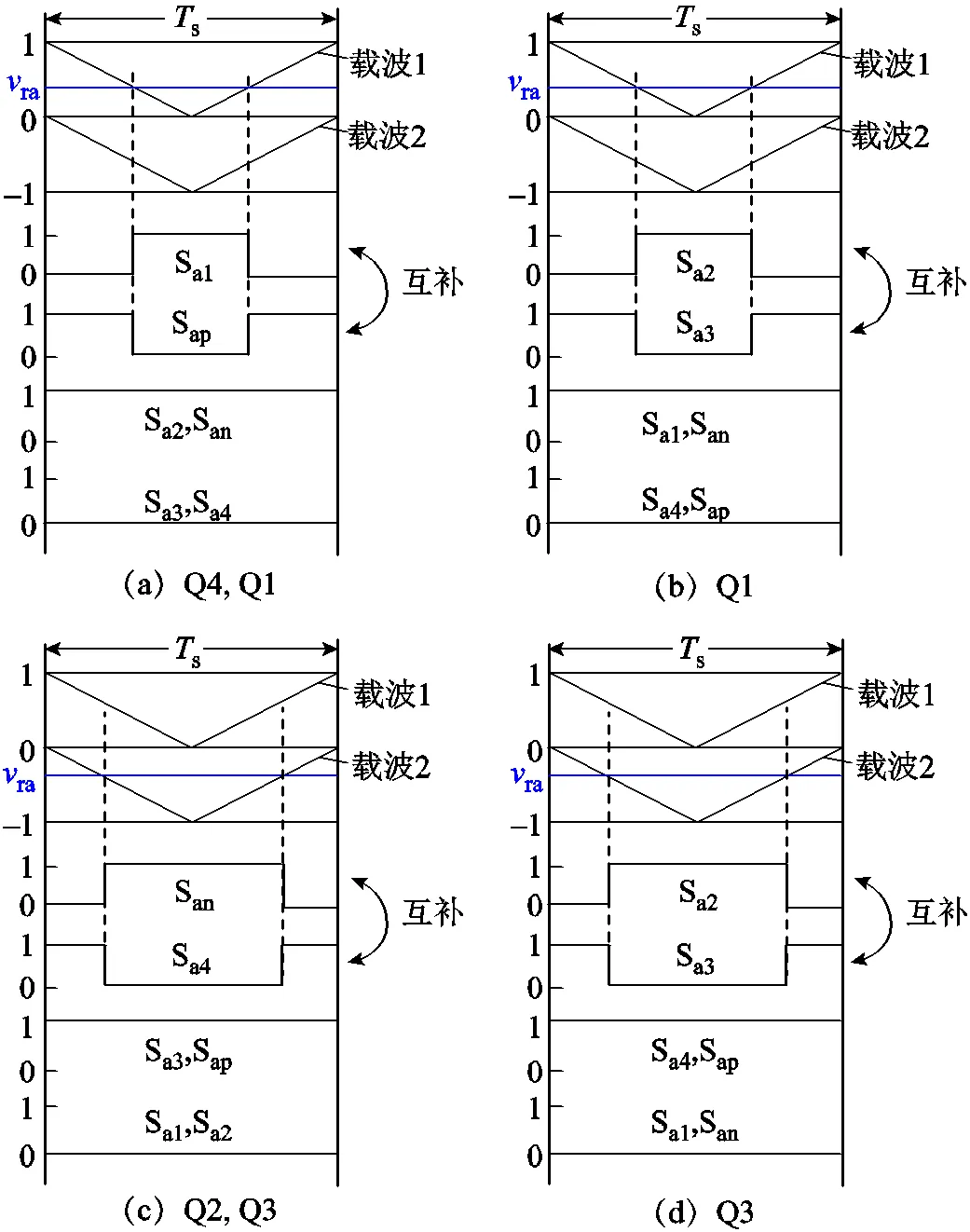
图5 损耗均衡策略下的底层驱动分配方法

3.2 模态持续角φ的求解

各开关管的导通损耗、开关损耗和总损耗分别记为P_con、P_sw和P_total(=Sa1～San)，则损耗均衡条件下满足

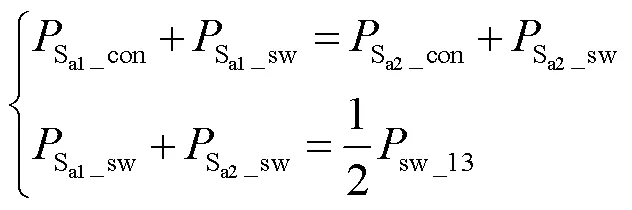
Sa1和Sa2各自的导通损耗和总开关损耗可由第2节得到。联立式（6）和式（7）可解得，Sa1和Sa2各自需承担的开关损耗，则进一步可解得为

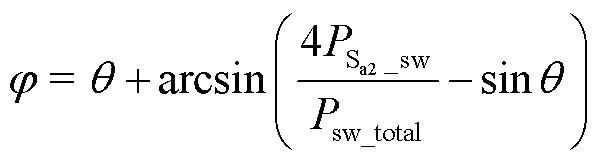
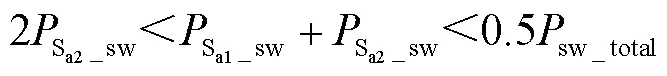
4 TZCC下的效率提升方法

4.1 驱动时序重构

当两条零电平钳位回路同时导通时，需要对图5的驱动分配方法重新调整，调整结果如图6所示。

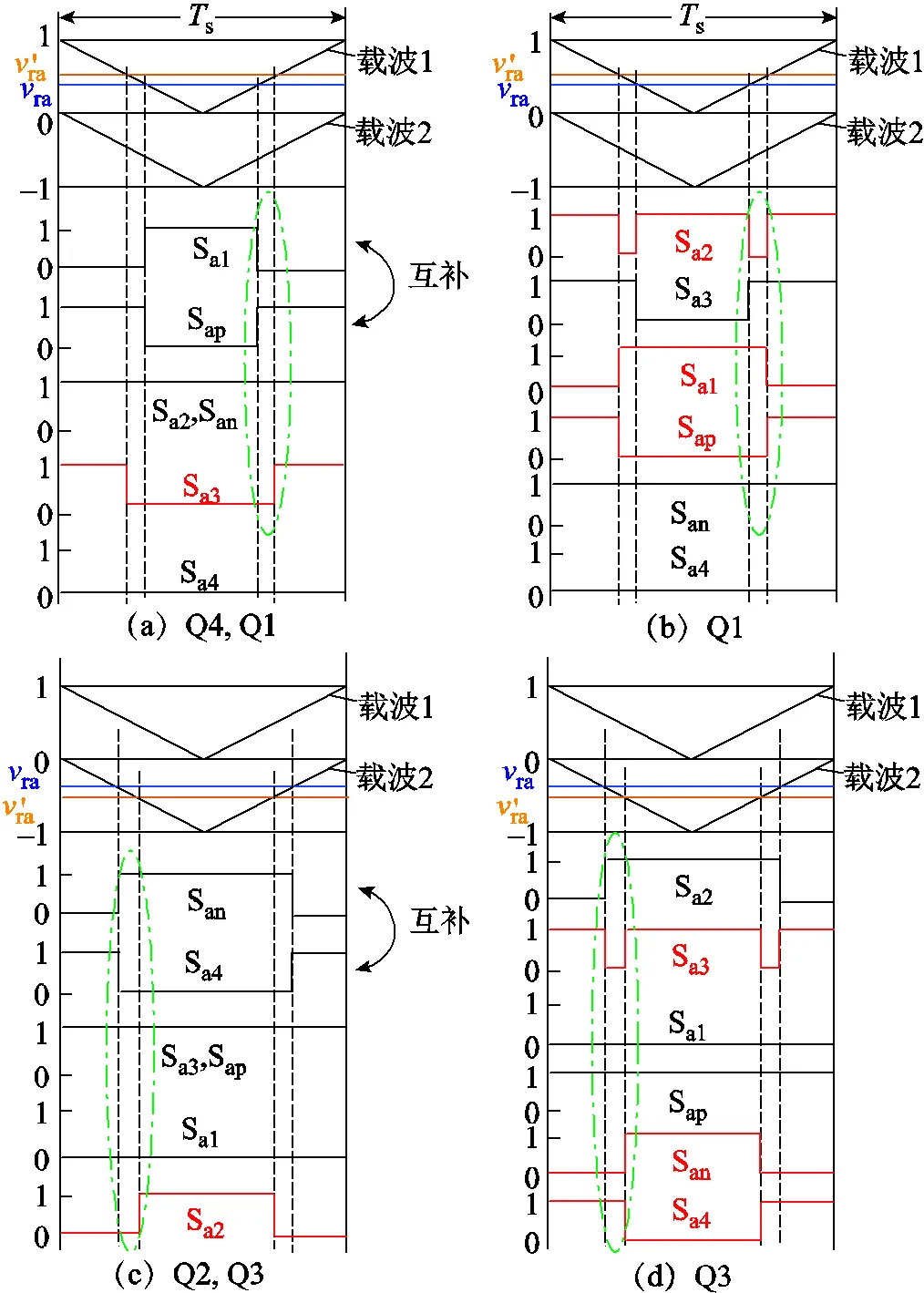
图6 TZCC策略下的驱动重构方法

具体的改动说明如下

（1）图6a中，在Sap导通后将Sa3开通，滞后时间为z，此时开关管Sa2、Sa3、Sap和San同时导通，保证了两条零电平回路同时续流，又因为Sa3开通前，与之并联回路Sa2与Sap已经导通，此时Sa3不承担开通损耗；同理，在Sap关断前先将Sa3关断，超前时间同为z，则Sa3也不承担关断损耗。因此在减小导通损耗的同时并不会增加额外的开关损耗。

（2）图6b中，桥臂电压由P状态向O状态切换时，当Sa2与Sa3换流完成后，则Sa3与San构成的钳位回路已经导通，为了满足TZCC条件，必须先关断Sa1，否则正母线电容将直通短路，再同时开通Sa2和Sap，此时Sa2与Sap不承担开通损耗；又因为Sa1延迟Sa2关断，因此也不承担关断损耗。当桥臂电压由O状态向P状态切换时，则需要提前z时间关断Sa2和Sap，再开通Sa1，恢复到Sa2与Sa3的预备换流模态，该阶段下Sa1同样不承担开通损耗，而Sa2和Sap也不承担关断损耗。

（3）图6c中，与图6a类似，在San导通后将Sa2也开通，滞后时间为z；在San关断前先将Sa2关断，超前时间同为z，同理Sa2实现了零电压软开关（Zero Voltage Switching, ZVS）。

（4）图6d中，与图6b类似，桥臂电压由P状态向O状态切换时，当Sa3与Sa2换流完成后，则Sa2与Sap构成的钳位回路已经导通，此时需要先关断Sa4，再同时开通Sa3和San。当桥臂电压由O状态向P状态切换时，则需要提前z时间关断Sa3和San，再开通Sa4，恢复到Sa3与Sa2的预备换流模态，该阶段下Sa3、Sa4和San均实现ZVS。

4.2 调制信号构造

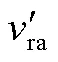
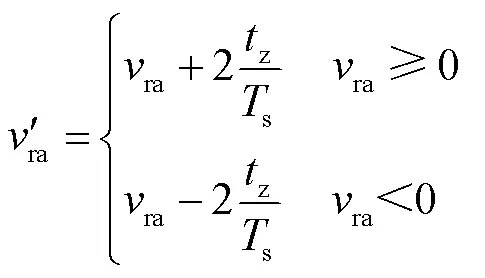
由于z在分配开关损耗上起着关键作用，需要保证在该时间内开关管能够完全可靠地开通和关断，因此满足

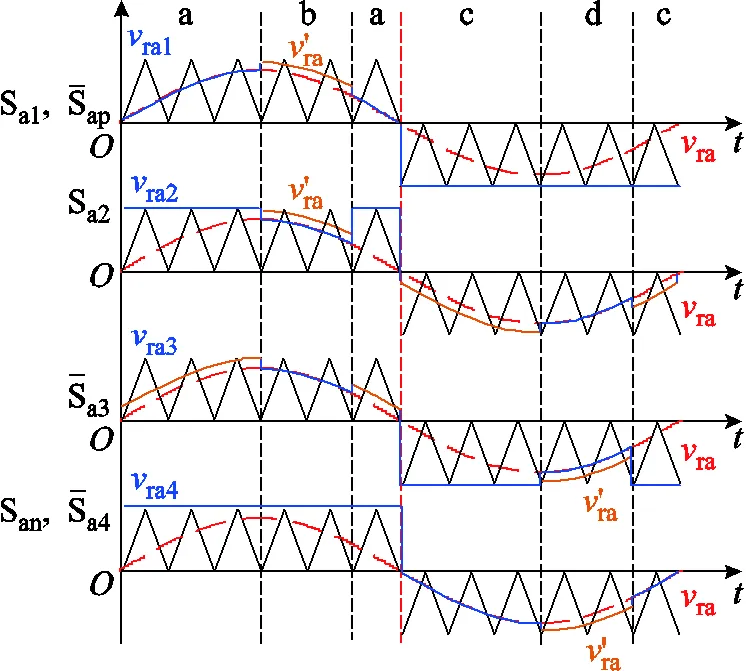
图7 TZCC策略下的调制信号波形

表1 TZCC方法下的调制信号

Tab.1 Modulation signals under TZCC method

对于同一个开关管，不同区域内开关动作次数也不同，因此DSP的PWM动作，子模块（AQ）配置不同，则在切换策略时需要采用影子寄存器，避免区域切换时刻造成驱动信号错误。

5 仿真与实验

开关器件的损耗估计结果直接影响模态持续角的大小，进而影响所提损耗均衡策略的效果。因此首先需要对损耗估计的可靠性进行相关验证；其次，在损耗评估正确的条件下，对所提损耗均衡策略进行验证；最后，对TZCC方法下所提驱动重构策略的可行性进行验证，同时得到对变换器运行效率提升的效果。

5.1 损耗估计可靠性验证

在评估损耗之前，根据第2节分析，需要根据所选开关器件对导通电阻温度修正系数1、开关损耗曲线及温度修正系数2和驱动电阻修正系数3进行拟合，拟合区间如图8所示。拟合结果如下：1=1.944×10-5j2+9.496×10-4j+0.9668；(ds)= 0.0169ds；2=(1.452×10-5j2+1.239×10-3j+ 1.271) / (1.452×10-5×252+1.239×10-3×25+1.271)；3= (0.1449g_ext+ 1.026)/(0.1449×2.5 +1.026)。在正弦载波调制方式下，以ANPC-1底层驱动分配方式为例，结合式（1）和式（3），各开关管的理论损耗计算见表2。

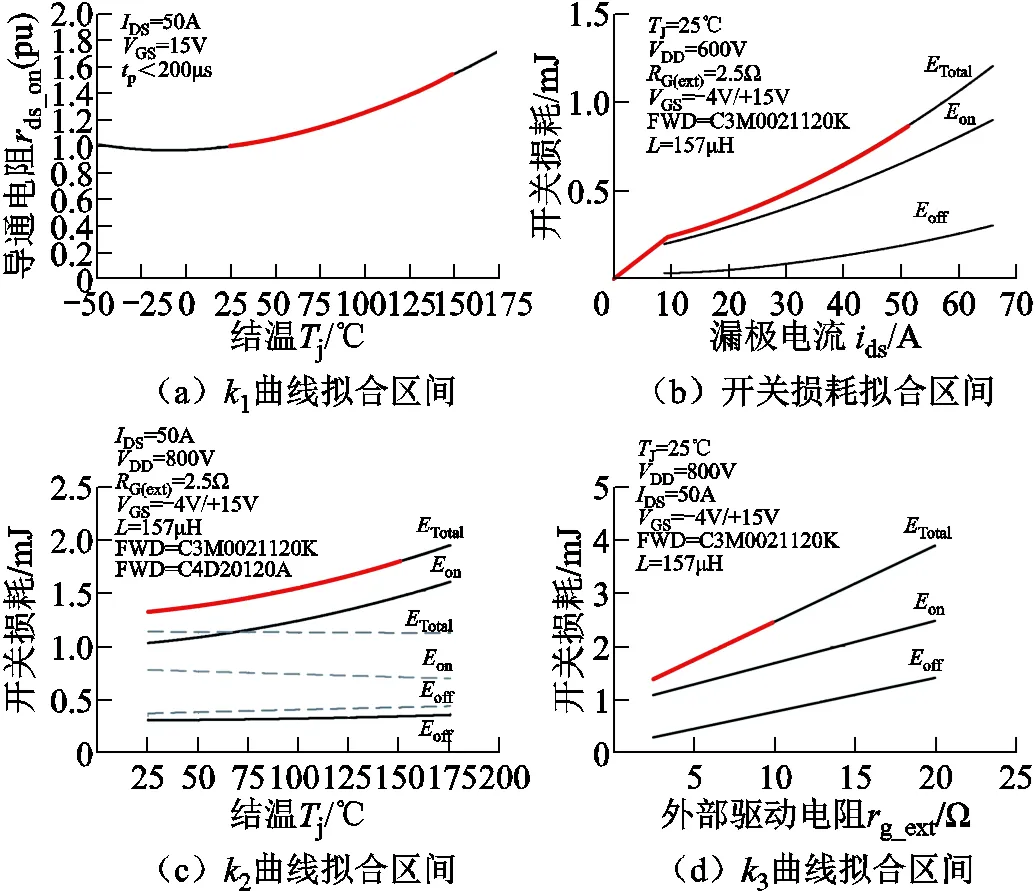
图8 损耗估计下的各参数拟合区间

表2 参数拟合下的各开关管理论损耗

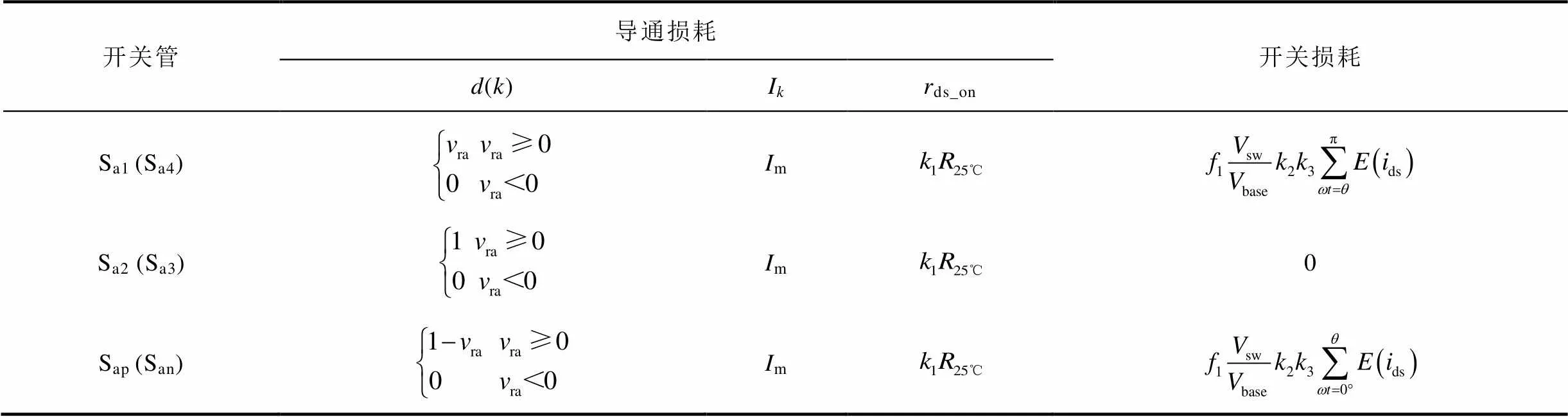
Tab.2 Theoretical loss under parameter fitting

在PLECS中搭建了ANPC单相电路，仿真模型关键参数见表3，输出接RL串联负载，保持负载阻抗幅值不变，功率因数角分别取为0°（= 9.6Ω，=1.6mH）、30°（= 8.3Ω，= 15.3mH）、60°（= 4.8Ω，= 26.5mH）和90°（= 0Ω，= 30.6mH）。注意需根据实验中的实际驱动电阻参数，在开关器件模型中做出相应的修改；损耗仿真假定散热器温度恒定，分别设定为25℃和125℃。

需要说明的是，由于各开关管温度不一致，因此各温度修正系数也不同，为简化计算过程，各开关器件损耗的温度修正系数1、2均假定相同，并按照所有开关管壳温的平均温度进行赋值。因为开关损耗与导通电阻随温度的变化特性曲线较为平稳，即使在温差范围较大时这种近似也可以被接受。

ANPC-1方法在25℃、125℃下的损耗仿真结果分别如图9和图10所示，SW表示开关损耗，Con表示导通损耗，为方便比较，理论损耗计算结果也在图9和图10中给出，即折线所示。在ANPC-1驱动分配方式下，当功率因数角为0°时，开关损耗全部加在Sa1（Sa4）上，此时损耗差异最为严重；随着功率因数角的增加，开关损耗逐步向Sap（San）转移，与理论分析一致，Sa2（Sa3）为工频开关，因此不存在开关损耗，且导通损耗几乎保持不变；当功率因数角为90°时，Sap（San）总损耗最大，但各开关管损耗差异并不大。

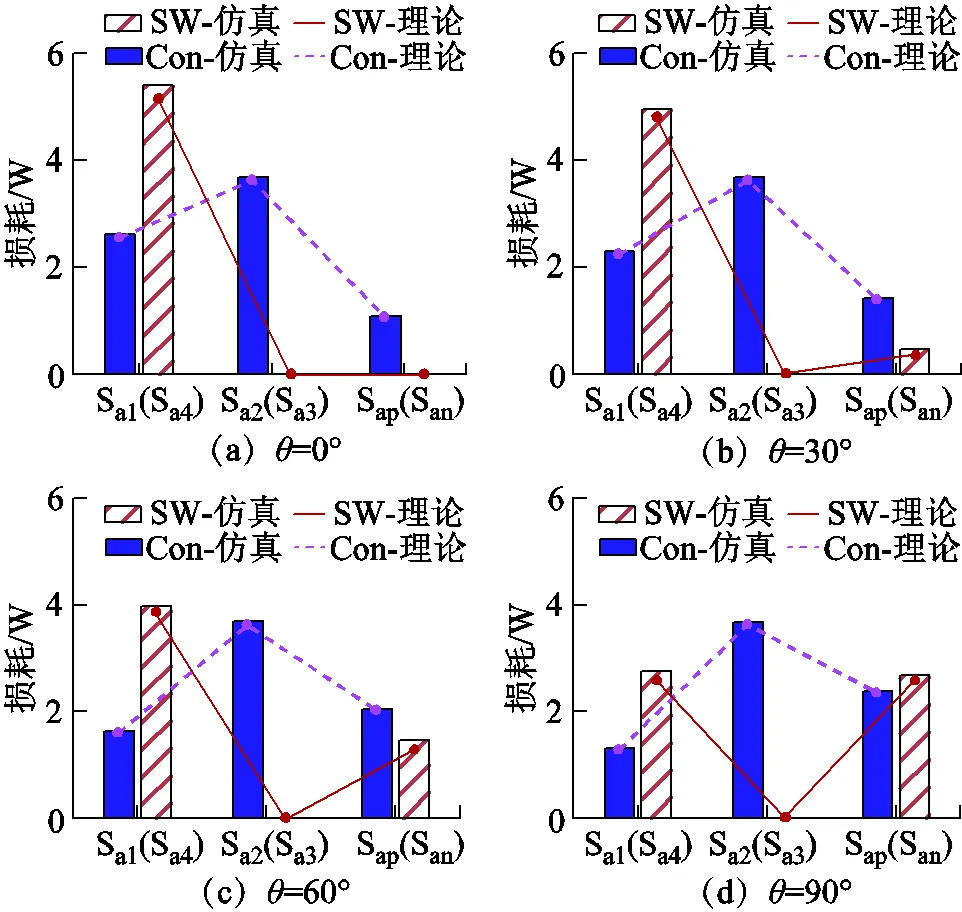
图9 ANPC-1方法25℃下的损耗仿真结果

图10 ANPC-1方法125℃下的损耗仿真结果

可以看出，在两组不同温度条件和功率因数角下，开关损耗和导通损耗的理论计算和仿真结果基本保持一致，证明了损耗估计方法的正确性。

5.2 损耗均衡策略效果验证

5.2.1 仿真证明

定义ANPC-B为ANPC-1采用了所提均衡策略后的方法，ANPC-TZCC-B为结合了驱动重构和均衡策略后所提的方法。均衡前后的损耗分布对比（50℃）如图11所示。图11a和图11b显示了两种方法下损耗分布的仿真结果，实线为理论计算结果。为便于比较，ANPC-1方法的损耗分布也在图11c中给出。另外，根据式（8）求解的两种方法下模态持续角与功率因数角的关系显示在图11d中。

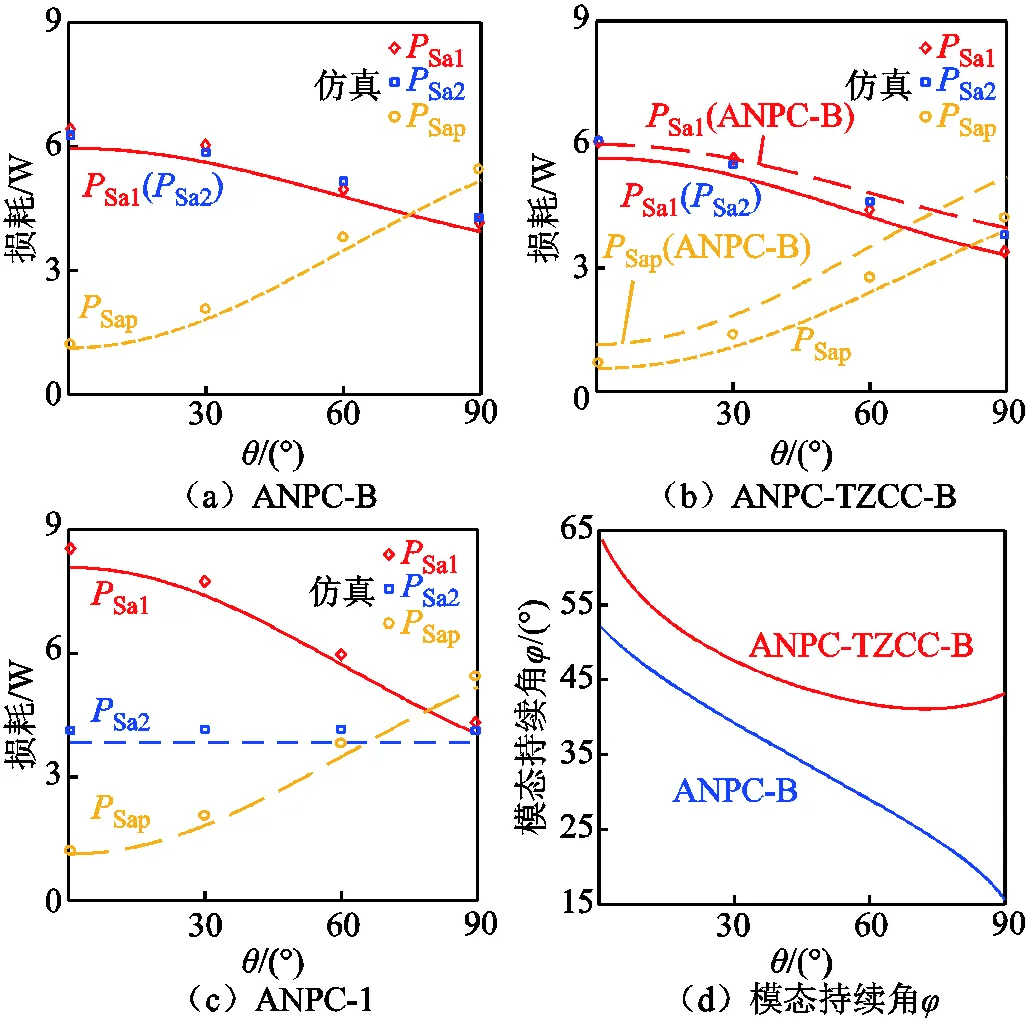
图11 均衡前后的损耗分布对比（50℃）

可以发现，随着功率因数角发生变化，两种方法下的主桥臂开关管损耗始终能保持均衡，证明了所提策略的有效性。另外，通过对比可以发现，当采用TZCC方法下的损耗均衡策略时，相比于单条钳位回路，其导通损耗更低，因此所有开关器件的损耗均下降，而变换器也具有更高的效率。

5.2.2 热平衡实验验证

基于ANPC单相电路，搭建实验平台，ANPC单相电路实验平台如图12所示，关键参数见表3，与仿真保持一致。温度测量仪器型号为testo875-1i（9Hz），待开关器件温度稳定后（30min）进行测量，待温度降回至室温后进行下一组对比实验。

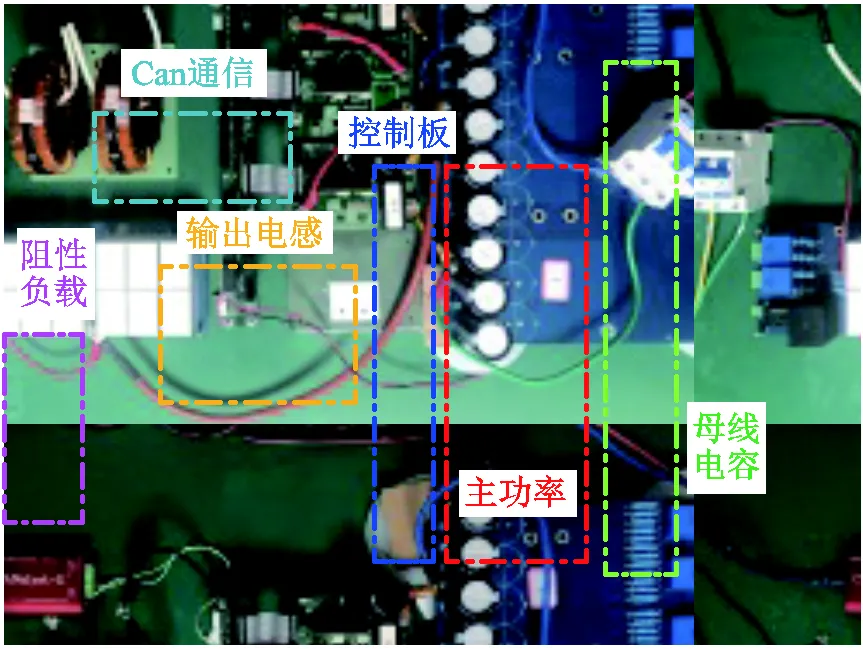
图12 ANPC单相电路实验平台

表3 ANPC单相电路仿真与实验参数

Tab.3 Simulation and experimental parameters of ANPC single-phase circuit

实验条件下考核损耗分布差异最为严重的情况，即功率因数角为0°。不同驱动分配方式下的实验温度特性如图13所示。在ANPC-1下，如图13a所示，Sa1稳定温度为59.2℃，Sa2为49.9℃，San温度最低为42.4℃。可以看到，当外管承受全部的开关损耗时，温度比内管高出接近10℃。当采用损耗均衡策略后，如图13b所示，Sa1与Sa2均接近54.5℃，均衡效果明显，所有开关器件中的最高温度下降了4℃。

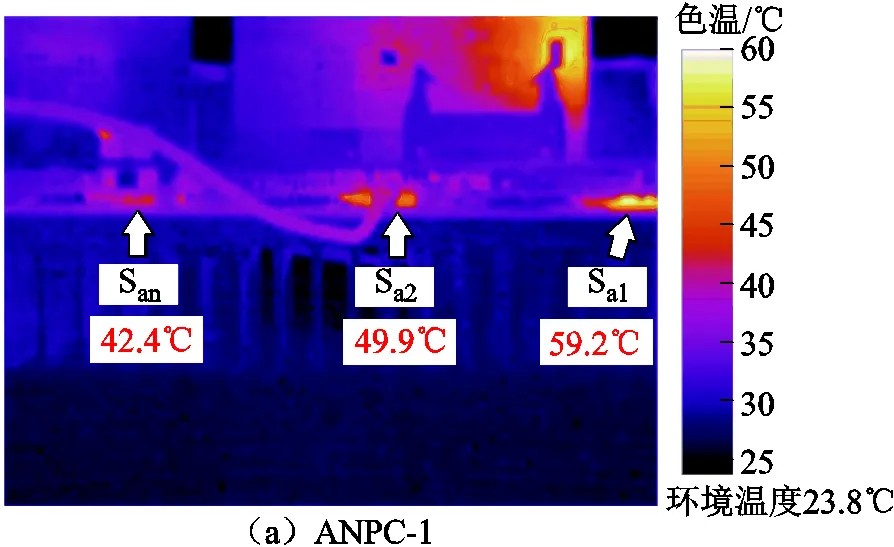
同理，在ANPC-TZCC-B驱动方式下，如图13c所示，Sa1与Sa2向中间温度靠拢，接近53.5℃，均衡效果明显，所有开关器件中的最高温度下降了4.3℃。

5.3 效率提升验证

1）理论分析

忽略死区时间对导通损耗的影响，在表3的参数下，理论上可以得到三种驱动方式下的总导通损耗曲线，如图14所示。对于ANPC-1和ANPC-B方法，由于采用单钳位回路，其不同电流路径下导通电阻相同，因此总导通损耗不随功率因数角的变化而变化。对于ANPC-TZCC-B两条钳位回路导通方式，其并联钳位回路导通电阻减小，而钳位回路电流有效值将随着功率因数角的增加而增大，因此总导通损耗随功率因数角的增加而下降。当功率因数角为0°时，导通损耗相比ANPC-1和ANPC-B方法下降15%，当功率因数角为90°时，导通损耗下降达32%。

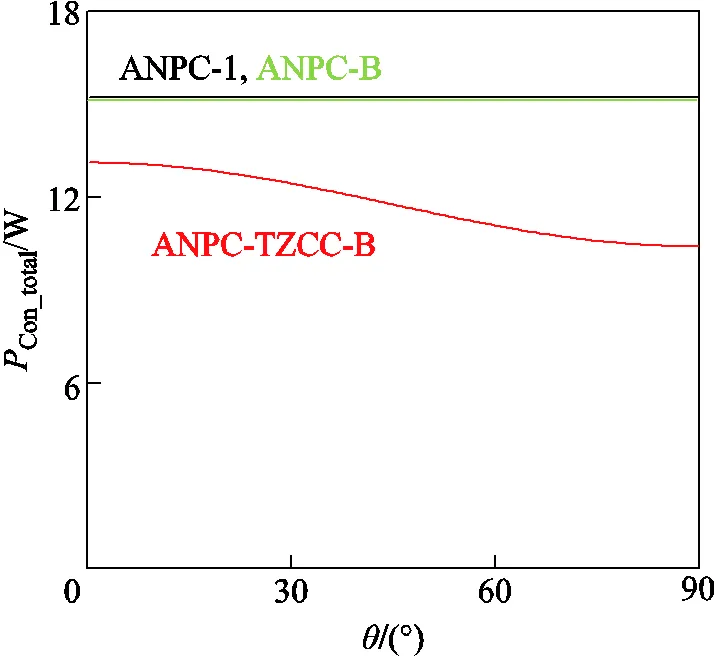
图14 三种驱动分配策略下的总导通损耗

2）实验验证

在功率因数角为0°时对三种驱动分配方法进行效率实验，输出电阻负载变化范围为8～24Ω，输出功率变化范围为1.2～3.4kW，其他实验参数不变，得到的效率曲线如图15所示。可以发现ANPC-1与ANPC-B方法的效率基本保持一致，ANPC-TZCC-B方法的效率位于3条曲线的最上方，平均高出约0.2%。值得一提的是，当所提策略应用在大功率和低功率因数的情况下，钳位回路导通损耗占比增加，效率提升的会更为明显。

图15 四种驱动分配策略下的效率曲线

6 结论

对于ANPC逆变器，提出了一种损耗主动均衡策略。基于导通损耗和开关损耗的评估，在第1、3象限内分别采用外管和内管承担开管损耗，在第2、4象限内采用钳位管承担开关损耗，通过合理分配各模态的起始时间和持续时间，使得主桥臂开关损耗保持一致。并通过对驱动时序的调整和重新构造，结合TZCC方法，进一步提升了变换器的运行效率。本文方法特点如下：

1）所提均衡策略扩展到了变功率因数角和调制比的情况，更具有一般性，同时采用并联钳位回路同时导通的方式，在容量和效率提升上同时进行了优化。

2）所提损耗评估方法、均衡策略以及驱动重构方法不受顶层调制策略的限制，同样适用于其他等效零序注入下的调制策略。

3）所提方法仅是基于软件在驱动策略上做出的改变，因此可同样推广到硬件混合的ANPC模块上。

4）所有分析结果虽然是基于电流滞后于电压的情况，但当功率因数角为(-90°, 0)时，仅需要将在(0, 90°)下求得的模态持续角取负号即可，即-(-)，其他部分无需修改。

[1] 高瞻, 李耀华, 葛琼璇, 等. 适用于大功率三电平中点钳位整流器的SVPWM和DPWM策略研究[J]. 电工技术学报, 2020, 35(23): 4864-4876.

Gao Zhan, Li Yaohua, Ge Qiongxuan, et al. Research on SVPWM and DPWM strategies suitable for high power three-level neutral point clamped rectifier[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4864-4876.

[2] 於锋, 朱晨光, 吴晓新, 等. 基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制[J]. 电工技术学报, 2020, 35(10): 2130-2140.

Yu Feng, Zhu Chenguang, Wu Xiaoxin, et al. Two-vector-based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion[J]. Transactions of China Electrotechnical Society, 2020, 35(10): 2130-2140.

[3] Chen Quan, Wang Qunjing, Li Guoli, et al. The control of unequal power losses distribution in three-level neutral-point-clamped VSC[C]//2012 15th International Conference on Electrical Machines and Systems, Sapporo, 2012: 1-5.

[4] Bruckner T, Bemet S. Loss balancing in three-level voltage source inverters applying active NPC switches[C]//2001 IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, 2001: 1135-1140.

[5] 李科峰, 高山, 刘计龙, 等. 有源中点钳位五电平逆变器悬浮电容预充电控制策略[J]. 电工技术学报, 2022, 37(8): 2064-2075.

Li Kefeng, Gao Shan, Liu Jilong, et al. Floating capacitor pre-charging control strategy for five-level active neutral-point-clamped inverter[J]. Transactions of China Electrotechnical Society, 2022, 37(8): 2064-2075.

[6] 李倩倩, 夏蓉花, 刘战, 等. 有源中点钳位型三电平并网逆变器多目标优化预测控制[J]. 电气技术, 2021, 22(7): 13-18.

Li Qianqian, Xia Ronghua, Liu Zhan, et al. Multi-objective optimal model predictive control for active neutral-point-clamped three-level inverter[J]. Electrical Engineering, 2021, 22(7): 13-18.

[7] 徐帅, 孙振耀, 姚春醒, 等. 基于混合载波调制的三电平ANPC逆变器开路故障容错控制策略[J]. 中国电机工程学报, 2021, 41(15): 5329-5340.

Xu Shuai, Sun Zhenyao, Yao Chunxing, et al. Open-switch fault-tolerant control strategy for three-level ANPC inverter based on hybrid carrier modulation[J]. Proceedings of the CSEE, 2021, 41(15): 5329-5340.

[8] 罗龙, 李耀华, 李子欣, 等. 有源中点钳位型三电平逆变器开关器件损耗均衡调制方法[J]. 电工电能新技术, 2021, 40(4): 1-9.

Luo long, Li Yaohua, Li Zixin, et al. Loss equalization modulation method for switching devices of active neutral point clamped three-level inverter[J]. Advanced Technology of Electrical Engineering and Energy, 2021, 40(4): 1-9.

[9] 关清心. SiC & Si器件混合型高效率低成本中点钳位型三电平电路研究[D]. 武汉: 华中科技大学, 2018.

[10] Novak M, Šunde V, Čobanov N, et al. Semiconductor loss distribution evaluation for three level ANPC converter using different modulation strategies[C]// 2017 19th International Conference on Electrical Drives and Power Electronics, Dubrovnik, 2017: 170-177.

[11] Floricau D, Floricau E, Dumitrescu M. Natural doubling of the apparent switching frequency using three-level ANPC converter[C]//2008 International School on Nonsinusoidal Currents and Compensation, Lagow, 2008: 1-6.

[12] 娄修弢, 张犁, 陈永炜, 等. 4-SiC 3L-ANPC逆变器损耗均衡和效率优化调制策略[J]. 中国电机工程学报, 2022, 42(5): 1925-1933.

Lou Xiuzhen, Zhang Li, Chen Yongwei, et al. A dedicate modulation scheme for 4-SiC 3L-ANPC inverter with loss balanced distribution and efficiency improvement[J]. Proceedings of the CSEE, 2022, 42(5): 1925-1933.

[13] Deng Yi, Li Jun, Shin K H, et al. Improved modulation scheme for loss balancing of three-level active NPC converters[J]. IEEE Transactions on Power Electronics, 2017, 32(4): 2521-2532.

[14] Zhang Gang, Yang Yongheng, Iannuzzo F, et al. Loss distribution analysis of three-level active neutral-point-clamped (3L-ANPC) converter with different PWM strategies[C]//2016 IEEE 2nd Annual Southern Power Electronics Conference, Auckland, 2016: 1-6.

[15] Ma L, Kerekes T, Rodriguez P, et al. A new PWM strategy for grid-connected half-bridge active NPC converters with losses distribution balancing mechanism[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5331-5340.

[16] Jiao Yang, Lu Sizhao, Lee F C. Switching performance optimization of a high power high frequency three-level active neutral point clamped phase leg[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3255-3266.

[17] Jiao Yang, Lee F C. New modulation scheme for three-level active neutral-point-clamped converter with loss and stress reduction[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5468-5479.

[18] Chen Mengxing, Pan Donghua, Wang Huai, et al. Investigation of switching oscillations for silicon carbide MOSFETs in three-level active neutral-point-clamped inverters[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(4): 4839-4853.

[19] Zhang Di, He Jiangbiao, Madhusoodhanan S. Three-level two-stage decoupled active NPC converter with Si IGBT and SiC MOSFET[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 6169-6178.

[20] Guan Qingxin, Li Chushan, Zhang Yu, et al. An extremely high efficient three-level active neutral-point-clamped converter comprising SiC and Si hybrid power stages[J]. IEEE Transactions on Power Electronics, 2018, 33(10): 8341-8352.

[21] Woldegiorgis D, Wu Yuheng, Wei Yuqi, et al. A high efficiency and low cost ANPC inverter using hybrid Si/SiC switches[J]. IEEE Open Journal of Industry Applications, 2021, 2: 154-167.

[22] Zhang Li, Lou Xiutao, Li Chushan, et al. Evaluation of different Si/SiC hybrid three-level active NPC inverters for high power density[J]. IEEE Transactions on Power Electronics, 2020, 35(8): 8224-8236.

[23] Zhang Di, He Jiangbiao, Pan Di. A megawatt-scale medium-voltage high-efficiency high power density “SiC+Si” hybrid three-level ANPC inverter for aircraft hybrid-electric propulsion systems[J]. IEEE Transactions on Industry Applications, 2019, 55(6): 5971-5980.

[24] Feng Zhijian, Zhang Xing, Yu Shaolin, et al. Comparative study of 2SiC&4Si hybrid configuration schemes in ANPC inverter[J]. IEEE Access, 2020, 8: 33934-33943.

[25] Belkhode S, Shukla A, Doolla S. Enhanced hybrid active-neutral-point-clamped converter with optimized loss distribution-based modulation scheme[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3600-3612.

[26] 马昆, 施永, 苏建徽, 等. 考虑寄生参数的功率MOSFET开关损耗简化计算方法[J]. 电工技术学报, 2021, 36(增刊2): 591-599, 609.

Ma Kun, Shi Yong, Su Jianhui, et al. Simplified model of power MOSFET switching loss considering the parasitic parameters[J]. Transactions of China Electrotechnical Society, 2021, 36(S2): 591-599, 609.

Loss Equalization and Efficiency Optimization Strategy of Active Neutral Point Clamped Inverter

Wan Wenchao Duan Shanxu Yu Tianbao Mi Huiyao

（State Key Laboratory of Advanced Electromagnetic Engineering and Technology School of Electrical and Electronic Engineering Huazhong University of Science and Technology Wuhan 430074 China）

For active neutral point clamped (ANPC) inverter, loss estimation model of power devices is built based on the principle of switching loss distribution, and an online adjustable loss distribution method is proposed to minimize the loss difference between every power device, by means of reasonably allocating different switching devices to undertake the switching loss and regulating the starting time and duration time of each mode. The method is deduced in detail and extended to the cases of variable power factor angles, which shows simple implementation and good effectiveness. Moreover, when the terminal voltage is clamped to neutral point, two zero-level clamped loop conducting (TZCC) is utilized for freewheeling through the reconstruction of the driving signals, therefore, conduction loss is decreased and the efficiency is further improved. Compared with the traditional single objective of loss equalization or efficiency optimization, the proposed method can achieve them both, so as to give full play to the advantages of ANPC inverters. Finally, the effectiveness of the proposed strategy is verified by simulation and experiments.

Active neutral point clamped (ANPC) inverter, loss equalization, driving signals reconstruction, efficiency improvement

10.19595/j.cnki.1000-6753.tces.220269

TM46

国家重点研发计划资助项目（2018YFB0106300）。

2022-03-01

2022-05-25

万文超 男，1995年生，博士研究生，研究方向为三电平变换器控制和调制技术。E-mail：wanwenchao@hust.edu.cn

段善旭 男，1970年生，教授，博士生导师，研究方向为新能源及分布式发电技术、无线电力传输及船用电能变换与控制等。E-mail：duanshanxu@hust.edu.cn（通信作者）

（编辑 陈诚）