基于多特征融合的行星齿轮箱点蚀故障诊断研究
2022-10-14范志锋华鉴波
范志锋,华鉴波
(武昌工学院智能制造学院,湖北 武汉 430065)
0 引言
行星齿轮箱具有体积小、传动比大和承载能力强等优点,在煤矿机械、风力发电机和立体车库等领域有广泛应用[1-3]。齿面点蚀是一种常见的早期故障。点蚀早期,异常振动信号微弱,行星齿轮箱能正常运转,但随着点蚀坑面积的增大,齿轮强度持续降低,会出现裂纹甚至断齿现象,影响齿轮箱的正常运转。因此,开展行星齿轮箱点蚀故障诊断研究具有重要意义。
针对行星齿轮箱的故障诊断问题,多位学者开展了相关的研究[4-11]。取得了一些成果,但针对行星齿轮箱点蚀故障诊断问题研究较少。本文在现有研究的基础上,以行星齿轮箱点蚀故障为研究对象,通过刚柔耦合仿真获得健康和3种不同齿面点蚀的齿轮箱箱体振动信号,进行变分模态分解(VMD)后,计算每个本征模态函数(IMF)分量的能量值、峭度因子和信息熵,构建多维特征向量,最后采用支持向量机(SVM)对行星齿轮箱的4种状态进行识别。
1 基本原理
1.1 VMD原理
VMD 方法可自适应地将振动信号分解为k个基于中心频率与有限带宽滤波后模态,即IMFi(i=1,2,…,k)。VMD分解的实质是构造和求解变分问题[12]。
a.构造变分问题。
(1)
(2)

b.求解变分问题。
为求解上述约束性变分问题,引入惩罚因子α和拉格朗日乘子λ,变为非约束性变分问题,表达式为
L(IMFk,ωk,λ)=

(3)
通过多次迭代计算,寻找式(3)的最优解,求得模态分量IMFk和中心频率ωk。
1.2 多特征融合原理
当行星齿轮箱发生点蚀故障后,振动信号经VMD分解后得到的IMF分量会发生变化,IMF分量的能量[13]、峭度因子和信息熵也[14]会发生相应变化。因此,可以将能量、峭度因子和信息熵3种特征融合在一起,从不同角度揭示点蚀故障信号的特性,提高故障识别率。
IMF分量的能量值计算公式为
(4)
IMF分量的峭度因子计算公式为
KIMFi=E(IMFi-μIMFi)4/σIMFi4i=1,2,…,k
(5)
E为数学期望;μ为均值;σ为标准差。
IMF分量的信息熵计算公式为
(6)
pIMFij为IMFi分量分成N段,每段的分布概率。
1.3 故障诊断流程
本文以行星齿轮箱作为研究对象,通过刚柔耦合仿真实验模拟健康和3种不同点蚀故障的齿轮。首先,采集4种状态的齿轮箱箱体振动信号,选择合适的模态数k,进行VMD分解;接着,计算VMD分解后的各IMF分量的能量值、峭度因子和信息熵;然后,融合IMF分量的能量值、峭度因子和信息熵,构建高维特征向量,并分为训练样本和测试样本;最后,用训练样本对支持向量机(SVM)进行训练后,通过测试样本实现行星齿轮箱点蚀故障的识别,并检验采用多特征融合构建高维特征向量的合理性。行星齿轮箱点蚀故障诊断的流程如图1所示。

图1 行星齿轮箱点蚀故障诊断流程
2 振动仿真信号生成
2.1 刚柔耦合仿真模型建立
本文研究的行星齿轮箱主要参数如表1所示,其中行星轮的数量为4个。

表1 行星齿轮箱主要参数
基于SolidWorks、ANSYS和ADAMS建立健康和3种太阳轮点蚀故障状态下行星齿轮箱的刚柔耦合仿真模型。
3种太阳轮点蚀故障状态如图2所示。图2中,点蚀1是1个半径0.5 mm、深度0.2 mm的点蚀坑,点蚀2是3个半径0.5 mm、深度0.2 mm的点蚀坑,点蚀3是两边圆弧半径0.5 mm、中间直线长度6 mm、深度0.2 mm的点蚀坑。
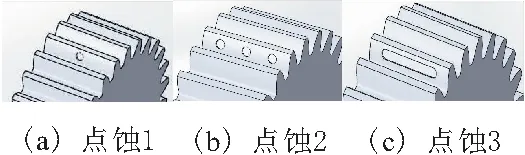
图2 3种太阳轮点蚀故障
本文对齿轮箱的箱体、太阳轮、行星架3个零件进行柔性化处理。其中,箱体在SolidWorks建立三维模型后,导出为“.x_t”格式的文件,然后导入ANSYS中,生成柔性体“.MNF”格式的文件,最终在ADAMS中导入箱体柔性体文件。太阳轮和行星架直接在ADAMS环境中利用ADAMS/Flex生成柔性体。在ADAMS中,合理设置各零件的材料、运动副、行星轮与太阳轮和齿圈的接触力等参数。最终生成的行星齿轮箱刚柔耦合模型如图3所示。

图3 行星齿轮箱刚柔耦合模型
2.2 信号生成
太阳轮作为输入,转频为30 Hz,在ADAMS中设置其运动为STEP(time,0,0,0.01,10800D)。行星架作为输出,负载设置为5 N·m,在ADAMS中设置其负载为STEP(time,0,0,0.01,5 000)。为反映齿轮箱的实际振动状态,本文设置的振动监测点位于输入轴轴承的正上方箱体处。
根据行星齿轮箱的结构参数,计算得到行星架的转频为6.562 5 Hz,行星轮的转频为-11.666 7 Hz。为全面反映行星轮与太阳轮的啮合过程,应保证每个样本行星轮至少自转1圈。本文取每个样本的仿真时间为0.1 s,此时行星轮转动1.17圈。
若每种状态获得50个样本数据,需要总仿真时间为5 s。每种状态仿真时,仿真时间为5.01 s,步长100 200。4种状态下仿真获得0.01~5.01 s箱体振动信号如图4所示。

图4 箱体振动时域信号
3 信号分析与处理
3.1 包络谱分析
对图4的4种状态的箱体振动仿真信号进行希尔伯特变换后得到的信号包络,再进行傅里叶变换,得到相应的包络谱信号,如图5所示。

图5 包络谱信号
从图5中可以看出,4种状态的包络谱信号中均显示了行星齿轮箱的啮合频率656.281 Hz(理论值656.250 Hz),同时3种太阳轮点蚀状态的包络谱信号中均显示了行星轮的故障频率93.689 Hz(理论值93.750 Hz)。上述结果验证了本文行星齿轮箱刚柔耦合仿真模型的正确性。
从图4和图5中,很容易区分行星齿轮箱的健康状态和点蚀状态,但从时域信号图和包络谱信号图中难以区分3种不同程度的点蚀状态。
3.2 信号VMD分解与特征向量构建
将图4所示的每种状态箱体振动信号等分为50个样本,共计200个样本。
对振动信号进行VMD分解时,模态数k决定了信号分解的精度,本文按照文献[15]给出的方法选择k,最终确定模态数k=5。
对200个样本振动信号进行VMD分解,按照式(4)~式(6)计算200个样本VMD分解获得的IMF分量时域信号的能量值、峭度因子和信息熵。
4种状态下IMF分量时域信号能量平均值、峭度因子平均值和信息熵平均值的区别如图6所示。图6中横坐标表示5个IMF分量。

图6 IMF分量不同特征参数区别
从图6中可以看出,若采用单一特征,部分IMF分量存在混叠现象,难以区别行星齿轮箱的4种状态。如图6a中,点蚀1和点蚀2的IMF1和IMF5分量的能量值存在一定的混叠现象;图6b中,点蚀1和点蚀2的IMF2分量的峭度因子混叠现象严重;图6c中,点蚀1、点蚀2和点蚀3的IMF5分量的信息熵混叠现象严重。为了提高点蚀故障诊断精度,融合IMF分量的能量值、峭度因子和信息熵,构建15维特征向量为
TIMF=(EIMF1,EIMF2,EIMF3,EIMF4,EIMF5,
KIMF1,KIMF2,KIMF3,KIMF4,KIMF5,
HIMF1,HIMF2,HIMF3,HIMF4,HIMF5)
(7)
4 点蚀故障识别
为准确识别行星齿轮箱的4种状态,采集200个(4×50)样本信号,随机选取其中的160个(4×40)样本信号作为训练样本,剩余的40个(4×10)样本信号作为测试样本,在MATLAB中用支持向量机分类器对健康和3种不同点蚀程度的齿轮状态进行识别。采用交叉验证方法,将160个训练样本中提取的15维特征向量作为SVM的输入量,对6种SVM分类器进行训练,验证准确度和训练时间如表2所示。

表2 6种SVM分类器的验证准确度和训练时间
从表2中可以看出,三次方核SVM分类器对本文研究的行星齿轮箱4种状态分析的验证准确度最高,而且训练时间较短。因此,选用三次方核SVM分类器对测试样本进行诊断。
将40个测试样本中提取的15维特征向量,用三次方核SVM分类器进行识别,故障诊断结果如图7所示。图7中,纵坐标表示测试样本的类别:1为健康,2为点蚀1,3为点蚀2,4为点蚀3。从图7中可以看出,4种状态的识别率均达到100%。
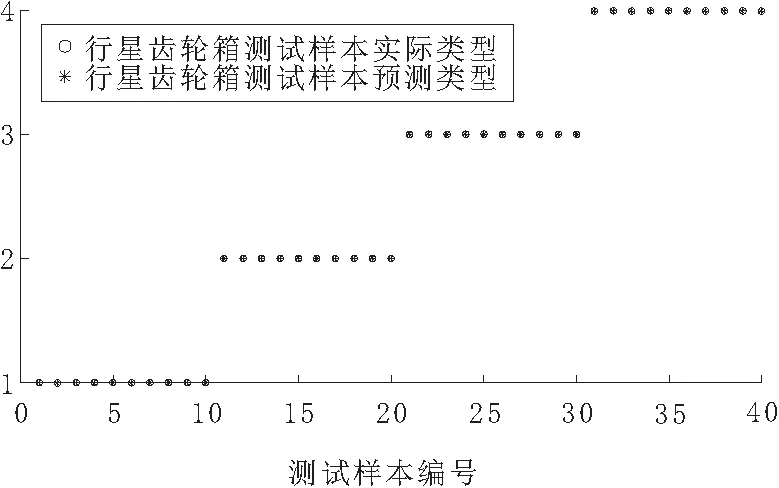
图7 行星齿轮箱点蚀故障诊断结果
单独采用IMF分量的能量值、峭度因子和信息熵构建5维特征向量,采用三次方核SVM分类器进行识别,故障诊断结果如图8所示。图8中,纵坐标表示测试样本的类别,与图7相同。

图8 5维特征向量故障诊断结果
从图7和图8中可以看出,采用15维特征向量的故障识别率明显高于5维特征向量的故障识别率,验证了本文提出的多特征融合对行星齿轮箱点蚀故障诊断的有效性。
5 结束语
本文提出了基于VMD和多特征融合的行星齿轮箱点蚀故障诊断方法。首先将刚柔耦合仿真获得的健康和3种不同点蚀程度齿轮箱箱体振动信号进行VMD分解,计算所有IMF分量的能量值、峭度因子和信息熵,基于能量值、峭度因子和信息熵构建15维特征向量,采用三次方核支持向量机分类器,选取160个样本作为训练样本,对支持向量机模型进行训练,最后对40个测试样本进行识别。结果表明,提出的多特征融合的行星齿轮箱点蚀故障总体识别率优于单一特征的行星齿轮箱点蚀故障总体识别率。
